
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two
Tank Systems
Claudia-Adina Bojan-Dragoş, Elena-Lorena Hedrea, Radu-Emil Precup,
Alexandra-Iulia Szedlak-Stinean and Raul-Cristian Roman
Department of Automation and Applied Informatics, Politehnica University Timisoara,
Bd. V. Parvan 2, Timisoara, Romania
Keywords: Vertical Two Tank Systems, MIMO Fuzzy Control, Nonlinear System, Experimental Results.
Abstract: The paper presents the design and validation of two control system (CS) structures for the level control of
vertical two tank systems. The first CS structure consists of a Multi Input Multi Output Proportional Integral
Fuzzy Controller with integration of controller input (MIMO–PI–FC–II) and the second CS structure consists
of a Multi Input Multi Output Proportional Integral Fuzzy Controller with integration of controller output
(MIMO–PI–FC–OI). The suggested CS structures are designed using the modulus optimum method and the
modal equivalence principle. The experimental results validate the proposed control solutions. Finally a
comparative analysis is also included.
1 INTRODUCTION
The vertical two-tank systems (V2TS) benchmark is
a nonlinear Multi Input-Multi Output process. An
overview of some recent control structures for the
level control in the two-tank systems includes: the
popular Proportional-Integral-Derivative (PID)
control (Dormido et al., 2008) neural networks (Na et
al., 2012), IFT–based linear and fuzzy control
(Precup et al., 2010), (Precup et al., 2013), switched
model predictive control (Mirzaee and Salahshoor,
2012), robust and fuzzy predictive control (Bouzouita
et al., 2008), gain-scheduling control (Chakravarthi et
al., 2014), (Dinesh Kumar and Meenakshipriya,
2012) or sliding mode control (Orani, 2009).
This paper is focused on the development of two
control system (CS) structures for the level control of
two tanks of vertical two tank systems. The first CS
structure consists of a Multi Input Multi Output
Proportional Integral Fuzzy Controller with
integration of controller input (MIMO–PI–FC–II)
and the second CS structure consists of a Multi Input
Multi Output Proportional Integral Fuzzy Controller
with integration of controller output (MIMO–PI–FC–
OI).
The paper is organized as follows: the nonlinear
model and the identified two-order benchmark-type
transfer functions (t.f.s) of the simplified models of
V2TS are given in Section 2. The proposed CS
structures are next developed in Section 3, and the
comparative study and the experimental results are
presented in Section 4. The conclusions are
highlighted in Section 5.
2 PROCESS MATHEMATICAL
MODELING
The V2TS is designed as a laboratory equipment that
allows for convenient experiments. The process
models consist of the following first principles state–
space equations of the process (Inteco, 2007):
,,
),)/(/(
))/(/(
),/()/(
2211
max2222
max22112
111
2
1
1
HyHy
wbHHwcHR
wbHHwcHRH
waHRwaqH
HH
(1)
where
1
ukq
EE
is the inflow in time,
1
u
is the control
input of the first tank,
4
106.1
EE
k
,
i
H
,
2,1i
, is
the fluid level of
th
i
tank,
i
,
2,1i
, is the flow
coefficient for
th
i
tank,
i
R
,
2,1i
, is the resistance of
the output orifice of
th
i
tank,
)(
ii
H
,
2,1i
, is the
cross sectional area of
th
i
tank computed at the level
810
Bojan-Drago¸s, C., Hedrea, E., Precup, R., Szedlak-Stinean, A. and Roman, R.
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two Tank Systems.
DOI: 10.5220/0007978508100817
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 810-817
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

i
H
,
Hi
y
,
2,1i
is the measured fluid level, and
12
Ru
is the control input of the second tank. The
block diagram of linear V2TS is given in Fig. 1.
Figure 1: The block diagram of linear V2TS models.
The parameters have the following numerical
values:
5
1
1008.11
R
,
5
2
1078.8
R
,
5.0
21
,
25.0a
,
345.0b
,
1.0
c
,
035.0w
,
4
10435.0
q
,
35.0
max2max1
HH
.
In order to design the proposed control solutions,
the nonlinear state-space equations (1) were
approximated to two second–order benchmark-type
t.f.s using a simple least–squares–based experimental
approximation of V2TS (Bojan-Dragos et al., 2018)
and considering zero initial conditions:
)1)(1()(
)(
)(
,
)1)(1()(
)(
)(
22
2
2
11
1
1
212
2
211
1
sTsT
k
su
sy
sH
sTsT
k
su
sy
sH
HH
PC
H
P
HH
PC
H
P
H
H
H
H
(2)
where
25.0,26.0
21
HH
PCPC
kk
are the controlled
process gains and
100,57,72
211
121
HHH
TTT
,
50
2
2
H
T
are the time constants.
Using the t.f.s. (2), the following state-space
matrices
},{,,,
21
HHj
jjj
CBA
are obtained:
.1052.00
,
0
1
,
01
102.003.0
,1064.00
,
0
1
,
01
1024.01032.0
4
3
5
42
2
22
1
11
H
HH
H
HH
C
BA
C
BA
(3)
3 DESIGN OF LEVEL CONTROL
SOLUTIONS
In order to obtain the desired liquid level of the two
tanks, H
1
and H
2
, two types of fuzzy control
structures, namely MIMO PI fuzzy controller with
integration of controller input (MIMO–PI–FC–II)
and MIMO PI fuzzy controller with integration of
controller output (MIMO–PI–FC–OI) were designed
in the following paragraphs.
3.1 Design of MIMO PI Fuzzy
Controller with Integration of
Controller Input (PI-FC-II)
The block diagram of the control structure with
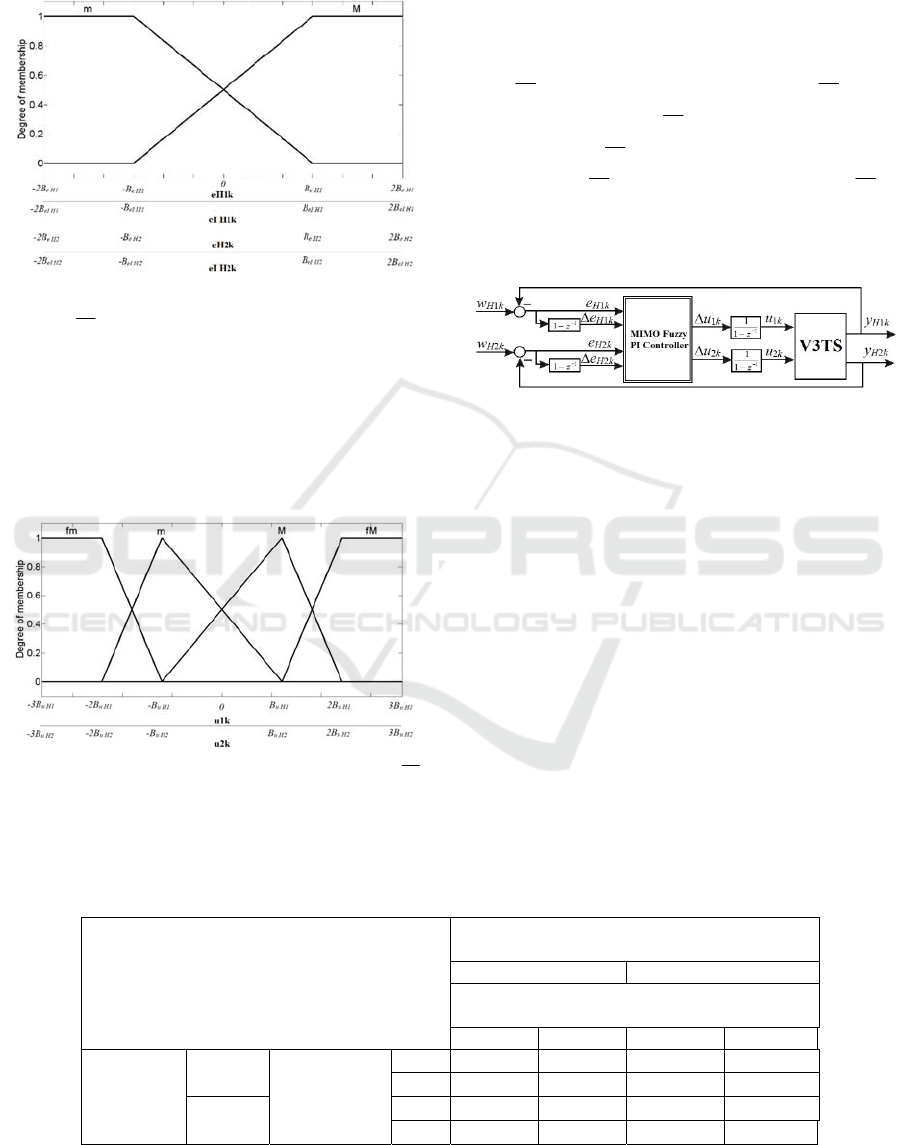
MIMO–PI–FC–II is illustrated in Fig. 2, where
Hik
w
,
2,1i
is the reference input,
Hik
e
,
2,1i
is the
control error,
IkHi
e
,
2,1i
is the integral of control
error,
ik
u
,
2,1i
is the control input,
Hik
y
,
2,1i
is
the controlled output.
Figure 2: Block diagram MIMO–PI–FC–IICS.
The PI-FC-II design is formulated from the
continuous-time PI controller design:
}2,1{),1)](/([)(
iTsTsksH
HiHiHi
Hi
ccCC
(4)
where:
Hi
C
k
– gain and
Hi
c
T
– integral time constant.
Tustin’s method with
s 01.0
s
T
was used in order
to discretize this PI controller and the obtained quasi-
continuous digital PI controller is:
}2,1{],)/1([
ieeK
eKeKu
kHiHiIkHiHiI
kHiHiPIkHiHiIik
(5)
where the expressions of the PI controller tuning
parameters,
HiP
K
and
HiI
K
, are
)2/(2/
,/ ,)]2/(1[
scsHiPHiIHi
csCHiIcsCHiP
TTTKK
TTkKTTkK
Hi
HiHiHiHi
(6)
The fuzzification employs two linguistic terms
with trapezoidal membership functions for the input
variables,
kHi
e
and
IkHi
e
,
2,1i
, and four linguistic
terms with triangular and trapezoidal membership
functions for the output variables,
ik
u
,
2,1i
. The
membership functions are given in Fig. 3 and Fig.4.
The parameters of MIMO–PI–FC–II block
HieHiPHiuHieHieIHie
BKBBBB
,)/1(,
,
2,1i
,
are chosen based on the modal equivalence principle
and the value of the parameter
0
e
B
can be set using
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two Tank Systems
811
the experience of the CS designer, but the stability of
the fuzzy control system is used in this paper in this
regard.
Figure 3: Membership functions of the inputs,
kHi
e
and
IkHi
e
,
2,1i
.
The inference engine employs Mamdani’s MAX-
MIN compositional rule of inference assisted by the
rule base presented in Table 1, which gives the
unified rule bases of both PI-FC-OI and PI-FC-II. The
centre of gravity method is used for defuzzification in
both cases (PI-FC-OI or PI-FC-II).
Figure 4: Membership functions of the outputs
ik
u
,
2,1i
.
3.2 Design of MIMO PI Fuzzy
Controller with Integration of
Controller Output (PI-FC-OI)
The block diagram of the control structure with
MIMO–PI–FC–OI is illustrated in Fig. 5, where
Hik
w
,
2,1i
is the reference input,
Hik
e
,
2,1i
is the
control error,
Hik
e
,
2,1i
is the increment of control
error,
ik
u
,
2,1i
is the increment of the control
input,
ik
u
,
2,1i
is the control input,
Hik
y
,
2,1i
is
the controlled output. As shown in Fig. 2 and Fig. 5,
the input variables are also scheduling variables of
both PI-FC-II and PI-FC-OI.
Figure 5: Block diagram MIMO–PI–FC–OICS.
The PI-FC-OI design is formulated from the PI
controller design with the t.f. expression given in (4).
Tustin’s method with
s 01.0
s
T
was used in order to
discretize the continuous-time PI controllers and the
following quasi-continuous digital PI controller is
obtained:
)(
kHiHikHiHiP
kHiHiIkHiHiPki
eeK
eKeKu
(7)
where the expressions of the PI controller tuning
parameters,
HiP
K
and
HiI
K
, are
)2/(2/
,/ ,)]2/(1[
sCsHiPHiIHi
csCHiICsCHiP
TTTKK
TTkKTTkK
Hi
HiHiHiHi
(8)
The fuzzification, the inference engine and the
defuzzification are done in similar manner as in case
Table 1: Decision table of PI-FC-II.
k
u
1
/
k
u
2
kH
e
1
mM
IkH
e
1
mM m M
kH
e
2
m
IkH
e
2
m fm / fm fm / fm M / M M / M
M fm / fm fm / fm M / M M / M
M m m / m m / m FM / FM FM / FM
M m / m m / m FM / FM FM / FM
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
812

of MIMO–PI–FC–II. The fuzzification employs two
linguistic terms with trapezoidal membership
functions for the input variables,
kHi
e
and
kHi
e
,
2,1i
and four linguistic terms with triangular and
trapezoidal membership functions for the output
variables,
ik
u
,
2,1i
. The membership functions
are similar to the ones given in Fig. 3 and Fig.4.
The parameters of MIMO–PI–FC–OI block
HieHiIHiuHieHieHie
BKBBBB
,,
,
2,1i
, are
chosen based on the modal equivalence principle, and
the value of the parameter
0
e
B
can be set using the
experience of the CS designer, but firstly it must be
chosen to ensure the fuzzy CS stability as shown in
the next section or using other results as, for instance,
those given in (Precup et al., 2014).
3.3 Stability Analysis
For performing the stability analysis, the dynamics of
the fuzzy controller is transferred to the process, and
this leads to the extended controlled process (EP),
illustrated in Fig. 6 (Precup and Preitl, 1997), where
a
{j, o} - the upper index corresponding to the type
of integration: a=o for integration on the output of the
fuzzy controller (for PI-FC-OI), a=j for integration
on the input of the fuzzy controller (for PI-FC-II),
T
IkHiHik
j
Hik
www
,
T
kHikHi
o
kHi
ww w
,
2,1i
with
kHi
w
is the reference input,
IkHi
w
is the
integral of reference input,
kHiIkHiIkHi
www
1
,
1
kHikHikHi
www
is the increment of
reference input;
T
IkHikHi
j
IkHi
eee
,
T
kHikHi
o
kHi
ee e
,
2,1i
with:
kHi
e
is the
control error,
IkHi
e
is the integral of control error,
kHiIkHiIkHi
eee
1
,
kHi
e
is the increment of control
error; the output vectors are
T
IkHikHi
j
kHi
yyy
,
T
kHikHi
o
kHi
yy y
,
2,1i
with:
kHi
y
is the
controlled output,
IkHi
y
is the integral of controlled
output,
kHiIkHiIkHi
yyy
1
,
1
kHikHikHi
yyy
is
the increment of controlled output;
T
kifki
j
ki
uuu
,
T
fikik
o
ki
uu u
,
2,1i
where
kif
u
represents the
fictitious control signal,
kif
u
stands for the
fictitious increment of control signal (Precup and
Preitl, 1997; Precup and Preitl, 2003a).
Figure 6: Modified structure of fuzzy control system.
The FC block is characterised by the nonlinear
input-output static map
F
T
a
k
a
k
fRR 0)()(,:
22
eeFF
(9)
where f (
RRf
2
:
) is the input-output static map
of the nonlinear blocks (FC).
The state-space mathematical models can be
expressed in terms of the following unified
expression for both PI fuzzy controllers:
a
kHi
aa
Hik
a
ik
aa
kHi
aa
kHi
xCy
uBxAx
1
(10)
by inserting additional state variables, which result in
the augmented state vectors
T
j
kHiykHi
j
kHi
xxx
for
PI-FC-II and
T
o
kHiykHiukHi
o
kHi
xxxx
for PI-FC-
OI, due to the presence of the additional linear
dynamics transferred from the PI fuzzy controller
structures (Precup and Preitl, 1997; Precup and Preitl,
2003a). Therefore the resulting state-space matrices
in case of PI-FC-II are
jjjj
xnjxnjxnnj
T
T
j
T
j
T
j
22
,,,
1
0
,
1
,
1
CBA
0
c
C
bc
1b
B
Ac
0A
A
(11)
and in case of PI-FC-OI are
oooo
xnoxnoxnno
T
T
o
o
T
To
22
,,
,
10
00
10
11,
00
01
CBA
c
c
C
1b
B
c
0
0bA
A
(12)
where
21, nnnn
oj
and n is the order of the
mathematical models.
The structure presented in Fig. 7 is used in the
stability analysis of the nonlinear control system,
where the NL block represents a static nonlinearity
due to the nonlinear part without dynamics of the FC
block.
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two Tank Systems
813
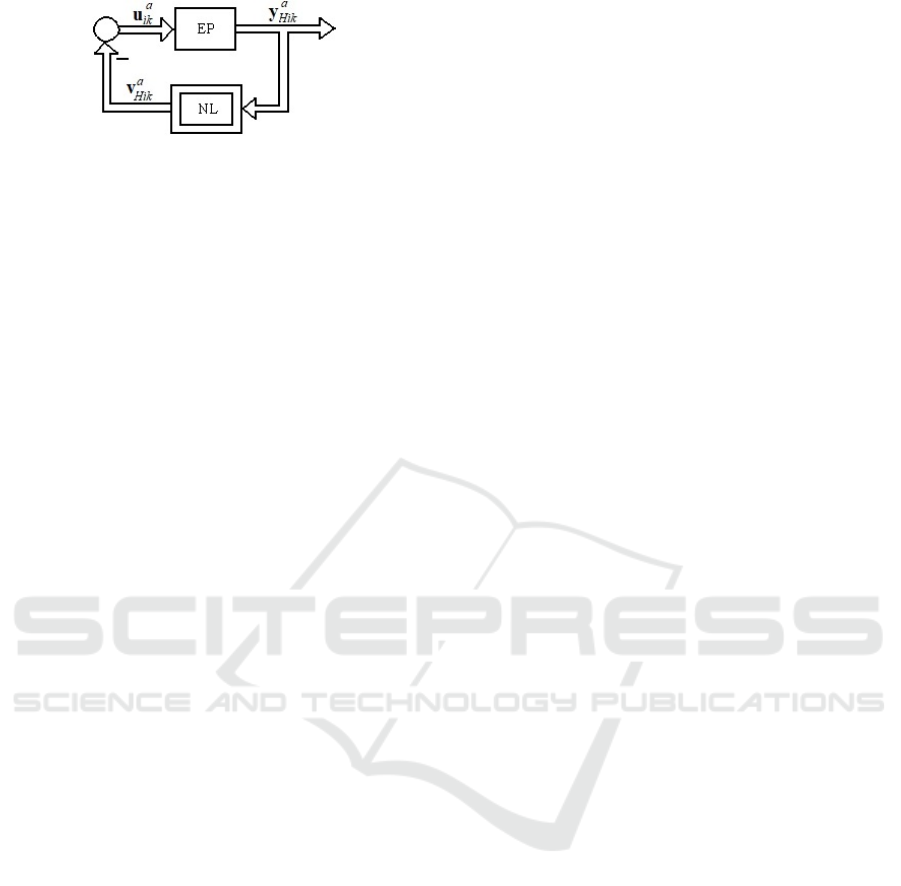
Figure 7: Structure of nonlinear control system involved in
stability analysis.
The connections between the variables of the
control system structures in Figs. 6 and 7 are
a
Hik
a
Hik
a
Hik
a
ki
a
Hik
eyeFuv ),(
(13)
where the second component of
F is always zero in
order to neglect the effect of fictitious control signal.
The second equation in (10) is next expressed as
follows using (13):
a
Hik
ba
Hik
a
ik
aa
Hik
eCxuCe ,
(14)
where the matrix
b
C
, (
2xnb
a
C
), can be computed
relatively easily as function of
a
C
.
The proposed stability analysis method can be
stated in terms of the following theorem:
Theorem. The nonlinear system, from Fig. 7 and
with the mathematical model (10), is globally
asymptotically stable if the three matrices
P
(positive definite,
aa
xnn
P
),
L
(regular, dim
aa
xnn
L
) and
V
(any,
2xn
a
V
) fulfil the
requirements I and II:
I.
VVBPB
LVAPBC
LLAPA
TaTa
TTaTaa
TaTa
)(
)(
)(
(15)
II. By introducing the matrices
M
(
22 x
M
),
N
(
22 x
N
) and
R
(
22 x
R
) defined as follows:
VVR
CBPAVLCN
CPLLCM
T
TaaTaTb
bTTb
)(2 )( [)(
) ()(
(16)
the inequality
0 )()(
a
Hik
Ta
Hik
a
Hik
Ta
Hik
f eMeene
(17)
holds for any value of the control error
Hik
e
, with the
vector
a
Hik
e
defined in (13) and n – the first column in
N
.
Proof. The condition I is the first equation in
Kalman-Szegö’s lemma, therefore it is fulfilled
immediately (Landau, 1979).
In order to fulfil the condition II, the Popov
inequality (17), which ensures the global asymptotic
stability of the nonlinear control system, Fig. 7, for
any positive constant β
0
, is expressed as
*
1
2
0
0
1
, )()(
1
NkkS
k
k
a
Hik
Ta
Hik
yv
(18)
Considering (13), the Popov sum
)(
1
kS
in (18) is
transformed in
*
1
0
1
)()(
1
NkkS
k
k
a
Hik
Ta
ik
yu
(19)
Substituting the expressions of
a
Hik 1
x
and
a
Hik
y
according to (10) in (19), followed by adding and
subtracting the term
a
Hik
Ta
Hik 11
)(
xPx
and using the
properties of matrix transposition, the Popov sum
)(
1
kS
becomes
*
111
0
1
]})(
)()(])(
)()[()(
)()({)(
1
Nk
kS
a
kHi
Ta
kHi
a
ik
aTaTa
ik
a
ik
Ta
aTTaTa
Hik
k
k
a
Hik
aTaTa
Hik
xPx
uBPBuuC
BPPAx
xAPAx
(20)
Replacing the expressions of
aTa
APA )(
,
aTTa
BPA )(
and
aTa
BPB )(
in terms of (I),
expressing
a
Hik
x
in accordance with (14) and using II,
another form of the Popov sum
)(
1
kS
is obtained:
*
1
0
0
111
])(
)()[(
)()(
1
1
Nk
kS
a
ik
Ta
ik
k
k
a
ik
Ta
Hik
a
Hik
Ta
Hik
k
k
a
kHi
Ta
kHi
uRu
uNeeMe
xPx
(21)
Using the expression of
a
ik
u
from (13), the sum in
(21) is expressed as
*
1
0
0
111
)]()(
)()()[(
)()(
1
1
Nk
kS
a
kHi
a
kHi
T
k
k
a
kHi
Ta
kHi
a
kHi
Ta
kHi
k
k
a
kHi
Ta
kHi
eFReF
eFNeeMe
xPx
(22)
Finally, the expression of the sum
)(
1
kS
is
obtained by using
F
from (9) and the positive
element r
11
of the matrix
R
:
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
814

*
1
0
2
11
0
111
])(
)[()](
)[()(
1
1
Nkf
fr
kS
a
kHi
Ta
kHi
k
k
a
kHi
Ta
kHi
a
kHi
k
k
a
kHi
Ta
kHi
ene
eMee
xPx
(23)
Both sums in the right-hand term of (23) are
positive and therefore the sum
)(
1
kS
is also positive,
which means that the condition II guarantees the
fulfilment of the Popov inequality (18).
In conclusion, the fuzzy control system is globally
asymptotically stable.
For n > 2, only the matrix
P
in (I is important for
the fuzzy CS stability analysis because the matrices
M
,
N
and
R
in II can be expressed as functions of
P
:
aTa
Ta
aTTaTb
baTaTb
BPBR
C
BPPACN
CAPACM
)(
])(
)()[()(
)()(
(24)
4 EXPERIMENTAL RESULTS
This section is dedicated to test and validate the two
proposed control structures, presented above by real-
time experimental results. The parameters of the
MIMO–PI–FC–II that ensure the stability of the fuzzy
control system are tuned as:
6.0,1008.1,15.0
1
3
11
HuHeIHe
BBB
,
36.0,1085.1,37.0
2
3
22
HuHeIHe
BBB
. The
parameters of MIMO–PI–FC–OI that ensure the
stability of the fuzzy control system are tuned as:
27.0
1
He
B
,
5
1
1088.1
He
B
,
,1005.7
4
1
Hu
B
5
2
5
22
1083.7,1013.3,45.0
HuHeHe
BBB
.
The following testing scenario was considered
and conducted: the two proposed control structures
were tested on the time frame of 1000 s with step–
type reference inputs which were set to
mw
kHi
1.0
,
2,1i
and are plotted in Fig. 8 and Fig. 9,
respectively, for both proposed CSs.
The tracking errors
Hik
e
for both the MIMO–PI–
FC–II–CS and MIMO–PI–FC–OI–CS are in fact the
control errors defined in Fig. 5. The mean square error
(MSE) was also calculated for both CSs as
2,1 ,))((
1
J
1
2
MSE
ite
N
N
t
dHik
d
Hi
(25)
where
100001
N
is the number of records, and the
obtained values are given in Table 2.
The conclusion drawn by analyzing the plots
given in Figs. 8 and 9, and after comparing the results
presented in Table 2, is that the zero steady state
control error is ensured for H
1
and H
2
in both the
proposed CSs and the best performances indices in
terms of settling time, rise time and mean square error
are obtained in case of MIMO-PI-FC-OI-CS.
Figure 8: Tank 1 fluid levels (H
1
) versus time (t) in case of
MIMO-PI-FC-II-CS and MIMO-PI-FC-OI-CS.
Figure 9: Tank 2 fluid levels (H
2
) versus time (t) in case of
MIMO-PI-FC-II-CS and MIMO-PI-FC-OI-CS.
Table 2: Mean Square Errors.
}2,1{,J
Hi
MSE
i
1
H
2
H
MIMO–PI–FC-II
4
108379.0
3
102208.0
MIMO–PI–FC-OI
4
108.0
3
102190.0
5 CONCLUSIONS
This paper has presented the design and validation of
two CSs applied to level control of V2TS. The first
CS structure consists of a Multi Input Multi Output
Proportional Integral Fuzzy Controller with
integration of controller input (MIMO–PI–FC–II)
and the second CS structure consists of a Multi Input
Multi Output Proportional Integral Fuzzy Controller
with integration of controller output (MIMO–PI–FC–
OI).The proposed control solutions were tested in the
same scenarios and their control performance is given
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two Tank Systems
815

in Table 2. The experimental results prove that the
best performances indices in terms of settling time,
rise time and mean square error are obtained in case
of MIMO-PI-FC-OI-CS.
Future research will be focused on the
improvement of the performance indices by
designing CSs with hybrid structures applied to
mechatronics systems that include large-scale
complex systems (Filip, 2008), robotics and
autonomous systems (Haidegger et al., 2012; Blažič,
2014; Kovács et al., 2016), model predictive control
(Bouzouita et al., 2008, Landau, 1979, Mirzaee and
Salahshoor, 2012), fuzzy models and control (Precup
and Preitl, 2003b; Precup et al., 2013; Johanyák,
2015; Olivas et al., 2017; Vrkalovic et al., 2018),
engines (Andoga et al., 2018), cognitive models
(Sánchez Boza et al., 2011; Direito et al., 2017;
Ferreira et al., 2017; Braga et al., 2019), and chaotic
systems (Precup et al., 2014; Köse and Mühürcü,
2018).
ACKNOWLEDGEMENTS
This work was supported by the CNFIS-FDI-2019-
0696 project of the Politehnica University of
Timisoara, Romania.
REFERENCES
Andoga, R., Főző, L., Judičák, J., Bréda, R., Szabo, S.,
Rozenberg, R., Džunda, M., 2018. Intelligent situational
control of small turbojet engines. International Journal
of Aerospace Engineering, 2018, paper 8328792, 1-16.
Blažič, S., 2014. On periodic control laws for mobile robots.
IEEE Transactions on Industrial Electronics, 61(7),
3660-3670.
Braga, D., Madureira, A. M., Coelho, L., Ajith, R., 2019.
Automatic detection of Parkinson's disease based on
acoustic analysis of speech. Engineering Applications of
Artificial Intelligence, 77, 148-158.
Bojan-Dragos, C.-A., Szedlak-Stinean, A.-I., Precup, R.-E.,
Grugui, L., Hedrea, E.-L., Mituletu, I.-C., 2018. Control
solutions for vertical three-tank systems, in
Proceedings of IEEE 13
th
International Symposium on
Applied Computational Intelligence and Informatics,
Timisoara, Romania, 593-598.
Bouzouita, B., Bouani, F., Wertz, W., Ksouri, M., 2008.
Implementation of SISO robust predictive control to a
three tanks system, in Proceedings of. IEEE
International Conference on Control Applications, San
Antonio, TX, USA, 323-328.
Chakravarthi, M. K., Pannem, V. K, Venkatesan, N., 2014.
Real time implementation of gain scheduled controller
design for higher order nonlinear system using
LabVIEW, International Journal of Engineering and
Technology, 6(5), 2031-2038.
Dinesh Kumar, D., Meenakshipriya, B., 2012. Design and
implementation of non linear system using gain
scheduled PI controller, Procedia Engineering, 38,
3105-3112.
Direito, B., Teixeira, C. A., Sales, F., Castelo-Branco, M.,
Dourado, A., 2017. A realistic seizure prediction study
based on multiclass SVM. International Journal of
Neural Systems, 27(3), 1-15.
Dormido, R., Vargas, H., Duro, N., Sanchez, J., Dormido-
Canto, S., Farias, G., Esquembre, F., Dormido, S.,
2008. Development of a web-based control laboratory
for automation technicians: the three-tank system, IEEE
Transactions on Education, 51, 35-44.
Ferreira, R., Graça Ruano, M., Ruano, A. E., 2017.
Intelligent non-invasive modeling of ultrasound-
induced temperature in tissue phantoms. Biomedical
Signal Processing and Control, 33, 141-150.
Filip, F. G., 2008. Decision support and control for large-
scale complex systems, Annual Reviews in Control,
32(1), 61-70.
Haidegger, T., Kovács, L., Precup, R.-E., Benyó, B.,
Benyó, Z., Preitl, S., 2012. Simulation and control for
telerobots in space medicine, Acta Astronautica,
181(1), 390-402.
Inteco, Multitank System, User’s Manual. Krakow, Poland:
Inteco Ltd., 2007.
Johanyák, Z. C., 2015. A simple fuzzy logic based power
control for a series hybrid electric vehicle, in Proceedings
of 9
th
IEEE European Modelling Symposium on
Mathematical Modelling and Computer Simulation,
Madrid, Spain, 207-212.
Köse, E., Mühürcü, A., 2018. The control of brushless DC
motor for electric vehicle by using chaotic
synchronization method, Studies in Informatics and
Control, 27(4), 403-412.
Kovács, B., Szayer, G., Tajti, F., Burdelis, M., Korondi, P.,
2016. A novel potential field method for path planning of
mobile robots by adapting animal motion attributes,
Robotics and Autonomous Systems, 82, 24-34.
Landau, I.D., 1979. Adaptive Control, New York, Marcel
Dekker, Inc.
Mirzaee, A., Salahshoor, K., 2012. Fault diagnosis and
accommodation of nonlinear systems based on
multiple-model adaptive unscented Kalman filter and
switched MPC and H
loop-shaping controller, Journal
of Process Control, 22(3), 626-634.
Na, J., Ren, X., Shang, C., Guo, Y., 2012. Adaptive neural
network predictive control for nonlinear pure feedback
systems with input delay, Journal of Process Control,
22(1), 194-206.
Olivas, F., Valdez, F., Castillo, O., González, C. I., Martinez,
G. E., Melin, P., 2017. Ant colony optimization with
dynamic parameter adaptation based on interval type-2
fuzzy logic systems. Applied Soft Computing, 53, 74-87.
Orani, N., Pisano, A., Usai, E., 2009. Fault detection and
reconstruction for a three-tank system via high-order
sliding-mode observer, in Proceedings of IEEE
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
816

International Conference on Control Applications,
Saint Petersburg, Russia, 1714-1719.
Popov, V. M., 1973. Hyperstability of Control Systems,
Berlin, Heidelberg, New York, Springer-Verlag.
Precup, R.-E., Preitl, S., 1997. Popov-type stability analysis
method for fuzzy control systems, in Proceedings of
Fifth European Congress on Intelligent Technologies
and Soft Computing (EUFIT), 2, Aachen, Germany,
1306-1310.
Precup, R.-E., Preitl, S., 2003a. Popov-type stability
analysis method for fuzzy control systems with PI fuzzy
controllers, Revue Roumaine de Sciences Techniques,
Electrotechnique et Energetique Series, 48(4), 505-
522.
Precup, R.-E., Preitl, S., 2003b. Development of fuzzy
controllers with non-homogeneous dynamics for
integral-type plants, Electrical Engineering, 85(3),
155-168.
Precup, R.-E., Mosincat, I., Radac, M.-B., Preitl, S.,
Kilyeni, S., Petriu, E.-M., Dragos, C.-A., 2010.
Experiments in iterative feedback tuning for level
control of three-tank system, in Proceedings of the 15
th
IEEE Mediterranean Electrotechnical Conference,
Valletta, Malta, 564-569.
Precup, R.-E., Tomescu, M.-L., Dragos, C.-A., 2014.
Stabilization of Rössler chaotic dynamical system using
fuzzy logic control algorithm, International Journal of
General Systems, 43(5), 413-433.
Precup, R.-E., Tomescu, M. L., Preitl, S., Petriu, E. M.,
Fodor, J., Pozna, C., 2013. Stability analysis and design
of a class of MIMO fuzzy control systems, Journal of
Intelligent & Fuzzy Systems, 25(1), 145-155.
Sánchez Boza, A., Haber Guerra, R., Gajate, A., 2011.
Artificial cognitive control system based on the shared
circuits model of sociocognitive capacities. A first
approach. Engineering Applications of Artificial
Intelligence, 24(2), 209-219.
Vrkalovic, S., Lunca, E.-C., Borlea, I.-D., 2018. Model-free
sliding mode and fuzzy controllers for reverse osmosis
desalination plants. International Journal of Artificial
Intelligence, 16(2), 208-222.
MIMO Fuzzy Control Solutions for the Level Control of Vertical Two Tank Systems
817
