
New Methodology for Backward Analysis of Reconfigurable Event
Control Systems using R-TNCESs
Yousra Hafidi
1,2,3,4 a
, Laid Kahloul
3
and Mohamed Khalgui
1,2 b
1
School of Electrical and Information Engineering, Jinan University, China
2
LISI Laboratory, National Institute of Applied Sciences and Technology, University of Carthage, Tunis 1080, Tunisia
3
LINFI Laboratory, Computer Science Department, Biskra University, Algeria
4
University of Tunis El Manar, Tunis, Tunisia
Keywords:
Reconfigurable Systems, Modeling and Verification, Petri Net, Backward Reachability, Model-base Diagnosis.
Abstract:
This paper deals with reconfigurable discrete event control systems (RDECSs). We model RDECSs using re-
configurable timed net condition/event systems (R-TNCESs) formalism which is an extension from Petri nets
to deal with reconfiguration properties. Model-based diagnosis algorithms are widely used in academia and
industry to detect faulty components and ensure systems safety. The application of these methods on reconfig-
urable systems is impossible due to their special behavior. In this paper, we propose accomplishing techniques
of backward reachability to make reconfigurable systems model-based diagnosis possible using R-TNCESs.
The flexibility among reconfigurable systems like RDECSs allows them to challenge recent requirements of
markets. However, such properties and complicated behavior make their verification task being complex and
sometimes impossible. We deal with the previous problem by proposing a new methodology based on back-
ward reachability of RDECSs using (R-TNCESs) formalism including improvement methods. The proposed
methodology serves to reduce as much as possible redundant computations and gives a package to be used in
model-based diagnosis algorithms. The paper’s contribution is applied to a benchmark modular production
system. Finally, a performance evaluation is achieved for different sizes of the problem to study benefits and
limits of the proposed methodology among large-scale systems.
1 INTRODUCTION
Nowadays flexibility in manufacturing systems is
challenging markets. For example, a system with fault
tolerance should be dynamic and respond without any
malfunction while hardware failures occur. Reconfig-
urable systems (Aissa et al., 2019; Hafidi. et al., 2019;
Ramdani. et al., 2019; Aissa et al., 2018) have flex-
ible configurations that allow them to switch from a
configuration to another in order to respond for user
requirements or to prevent from system malfunction
(Lakhdhar et al., 2018; Ramdani et al., 2018). How-
ever, their special behavior and properties of reconfig-
uration make of them complex discrete event systems.
In fact, any failure or dysfunction of a critical sys-
tem can result serious consequences. Reconfigurable
systems like reconfigurable discrete event control sys-
tems (RDECS) (Khalgui et al., 2004; Khalgui and
a
https://orcid.org/0000-0002-3543-6731
b
https://orcid.org/0000-0001-6311-3588
Mosbahi, 2010; Khalgui et al., 2007) are often sub-
jected to malfunctions that are due to hardware com-
ponents breakdowns or software dismisses. A safe
system should never reach an undesirable state during
its working process (Dubinin et al., 2015).
Many research works ensure safety of systems us-
ing methods such as Model-based Diagnosis (Cong
et al., 2017; Bennoui et al., 2009; Liu et al.,
2016). Model-based diagnosis (MBD) is a verifica-
tion method that explains an observed system’s mal-
function (De Kleer and Kurien, 2003). When an ab-
normal system’s behavior is observed, MBD method
backtracks system execution in the model, and com-
bines with predefined data to detect faulty compo-
nents that cause this behavior. Backward reachabil-
ity is frequently used to construct the backward state
space that serves with model checking responding to
system diagnosis problems. Model-checking (Baier
et al., 2008) is a verification technique that explores
possible system states in order to check if a sys-
tem meets its specifications. If a required property
Hafidi, Y., Kahloul, L. and Khalgui, M.
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs.
DOI: 10.5220/0007979901290140
In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 129-140
ISBN: 978-989-758-379-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
129

is proved false, model checking provides the coun-
terexample that falsified it. One of the main problems
is how to check the largest possible state spaces and
treat them as quick as possible with current means of
processors and memories. Existing research works
(Baier et al., 2008) have proven results for larger
systems state spaces by including some clever algo-
rithms. Consequently, more problems are covered.
Despite the advantage of system diagnosis
method, there still a lack of research works on diag-
nosis of reconfigurable systems. Their special behav-
ior as well as their reconfiguration properties (Wang
et al., 2011; Gharsellaoui et al., 2012; Ghribi et al.,
2018) should be taken into consideration. In addition,
the diagnosis of these complex systems like RDECSs
needs optimization methods that improve the process
and prevent unnecessary redundant computations.
In order to deal with previous problems, we pro-
pose in this paper the following contributions:
1. A backward reachability method for R-TNCESs
formalism to facilitate reconfigurable systems di-
agnosis: backward reachability is used rather
than forward reachability (for ordinary Petri nets,
colored Petri nets ...etc. (P
´
ozna et al., 2016;
Bhandari et al., 2018)) to solve systems diagno-
sis. R-TNCESs reverse rules and accomplishing
techniques are proposed to run backward reach-
ability of reconfigurable systems. Our motiva-
tion about using R-TNCESs formalism resides in
the way that unlike most other formalisms, R-
TNCESs are modular and support modeling of
system reconfigurations. In addition, the compo-
sition of interconnected modules communicating
with signals, deals with interactions that actually
happen between sensors and actuators in recon-
figurable discrete event control systems (Zhang
et al., 2013; Hafidi et al., 2018; Naidji et al.,
2018), i.e., sensors send signals to activate actu-
ators. By setting this method, the application of
classical algorithms of model-based diagnosis on
reconfigurable systems becomes possible using R-
TNCESs.
2. A new methodology to cover a wider state space
and resolve more problems. Diagnosis is a time
and space consuming problem, and the proposed
methodology in this paper includes improvement
methods that serve to prevent redundancies during
backward reachability analysis.
The purpose of this paper is to propose accomplishing
methods to allow the application of classical model
based diagnosis algorithms on reconfigurable systems
using R-TNCES formalism. Note that the problem
of applying the classical algorithms of model-based
diagnosis is left outside the scope of this paper.
To the best of our knowledge, (1) no existing
previous works have proposed methods for reconfig-
urable systems backward reachability, (2) no existing
rules showing how to reverse a system modeled by
R-TNCES formalism, and (3) no research works deal
with optimization of R-TNCESs backward state space
to improve model-based diagnosis abilities.
The paper’s contribution is applied to a real case
study: FESTO modular production system (FESTO
MPS) (Koszewnik et al., 2016; Khalgui et al., 2011),
which is an industrial reconfigurable benchmark plat-
form. Obtained results show that after applying pro-
posed methods, classical algorithms of model based
diagnosis becomes possible on R-TNCESs. In addi-
tion, the covered state space using new methodology
is improved. A performance evaluation is achieved
for different sizes of problems.
The remainder of the paper is organized as fol-
lows. Section 2 recalls the most recent basic ele-
ments of R-TNCESs formalism, introduces backward
reachability method concepts, presents the proposed
R-TNCES reverse method that will be used as a basic
element in backward reachability of R-TNCESs, and
finally reminds Mu method that will be used to im-
prove computations. Section 3 explains the main mo-
tivations of this paper, proposes the new methodology
of backward reachability including Mu improvement
method, presents the algorithm and computes its com-
plexity. Section 4 is the experimentation part which
contains some applications and results. Finally, Sec-
tion 5 concludes this paper and describes the future
work.
2 THEORETICAL
FOUNDATIONS
In this section we first introduce an extension from
Petri nets formalism (Qin et al., 2012) called reconfig-
urable discrete event/condition systems (R-TNCESs)
(Zhang et al., 2013; Zhang et al., 2017a). R-TNCESs
are used for formal modeling and verification of re-
configurable discrete event control systems. How-
ever, their verification is often expensive and needs
some improvement methods. In this section, we
present backward reachability analysis for R-TNCES
and some basic elements proposed to improve the ver-
ification task.
ICSOFT 2019 - 14th International Conference on Software Technologies
130

2.1 Reconfigurable Timed Net
Condition/Event Systems
According to the definition reported in (Zhang et al.,
2013; Hafidi et al., 2018), reconfigurable timed net
condition/event systems (R-TNCESs) are formally
defined by a couple RT N = (B, R) where B (respec-
tively, R) is the behavior (respectively, the control)
module of a reconfigurable discrete event control sys-
tem (RDECS). B is a union of multi-TNCESs repre-
sented by
B = (P, T, F, W, CN, EN, DC, V, Z
0
)
where,
• P (respectively, T ) is a superset of places (respec-
tively, transitions),
• F ⊆ (P × T) ∪(T × P)
1
is a superset of flow arcs,
• W : (P × T) ∪ (T × P) −→
{
0, 1
}
maps a weight
to a flow arc, W (x, y) > 0 if (x, y) ∈ F, and
W (x, y) = 0 otherwise, where x, y ∈ P ∪ T ,
• CN ⊆ (P × T ) (respectively, EN ⊆ (T × T )) is a
superset of condition signals (respectively, event
signals), (v) DC : F ∩ (P × T ) → {[l
1
, h
1
], . . . ,
[l
|F∩(P×T )|
, h
|F∩(P×T )|
]} is a superset of time con-
straints on input arcs of transitions, where ∀i ∈
[1, | F ∩ (P × T ) |] , l
i
, h
i
∈ N and l
i
< h
i
,
• V : T −→
{
∨, ∧
}
maps an event-processing mode
(AND or OR) for every transition,
• Z
0
= (M
0
, D
0
), where M
0
: P −→
{
0, 1
}
is the
initial marking, and D
0
: P −→
{
0
}
is the initial
clock position.
The graphical model of a TNCES is depicted in Fig.
1.
j
t
0
t
1
p
0
p
1
t
2
Event input
Flow arc
Forced transition
Token
Spontaneous transition
Module boundary
Event output
Condition signal / Condition arc
Signal arc / Event arc
Place
Figure 1: Modules graphical model.
R is a set of reconfiguration rules such that rule r is a
structure represented by
r = (Cond, s, x)
where,
1
Cartesian product of two sets: P × T = {(p, t)| p ∈
P, t ∈ T }.
• Cond →
{
True, False
}
is the pre-condition of r,
i.e., r is executable only if Cond = True,
• s : T N(
•
r) → T N(r
•
) is the structure-
modification instruction such that T N(
•
r)
(respectively, T N(r
•
)) represents the struc-
ture before (respectively, after) applying the
reconfiguration r,
• x : last
state
(
•
r) → initial
state
(r
•
) is the state pro-
cessing function. In this paper, we denote by r
i j
the reconfiguration rule that transforms T NCES
i
to T NCES
j
.
As reported in (Zhang et al., 2013; Hafidi et al., 2018),
structure-modification instructions are presented in
Table 1. A place is denoted by x, a transition by y,
a control component module by CC, and the AND
instruction to represent complex modification instruc-
tions is presented by “,”.
Table 1: Structure-modification instructions of R-TNCESs.
N° Instruction Symbol
1 Add condition signals Cr(cn(x, y))
2 Add event signals Cr(ev(y, y))
3 Add control component Cr(CC)
4 Delete condition signals De(cn(x, y))
5 Delete event signals De(ev(y, y))
6 Delete control component De(CC)
7
Add place x with
Cr(x, m(x))
its marking m(x)
8 Add transition y Cr(y)
9
Add flow arc f a(x, y) Cr( f a(x, y)) or
or flow arc f a(y, x) Cr( f a(y, x))
10 Delete place x De(x)
11 Delete transition y De(y)
12
Delete flow arc f a(x, y) De( f a(x, y)) or
or flow arc f a(y, x) De( f a(y, x))
13
Modify transition’s y event-
Mo(AND(y))
processing mode to “AND”
14
Modify transition’s y event-
Mo(OR(y))
processing mode to “OR”
R-TNCESs semantic is defined by both the recon-
figuration between TNCESs in behavior module B,
and the firing of transitions in each TNCES. The for-
mer has the priority to be applied first when its pre-
conditions are fulfilled. The latter depends on the
rules of firing transitions in TNCESs and the cho-
sen firing mode. Two kinds of transitions are distin-
guished, i.e., spontaneous and forced transitions. A
transition t is called spontaneous if it is not forced by
any other transition (i.e., there are no event signals in-
coming to t), otherwise it is called forced transition.
Each type of transitions has its firing rules. The firing
rules are described in detail in (Zhang et al., 2013).
However for the firing mode, we adopt the mode in
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs
131

which only “one spontaneous transition is fired by
step”.
We use the concept of control components (CCs)
which was firstly introduced in (Khalgui et al., 2011)
in order to model RDECSs. This means that each con-
figuration is a set of CCs interconnected with each
other to compose a TNCES. The concept of CCs
serves the modularity which enabels the readability
and the re-usability of models.
Note that in this paper, we use non marked
TNCESs which are TNCESs structures with no given
initial marking and non marked R-TNCESs which are
R-TNCESs with configurations represented by non
marked TNCESs. We use non marked R-TNCESs
to describe many possible systems in one model, i.e.,
each R-TNCES with a possible initial marking rep-
resents a system. In addition, by non marked R-
TNCESs we are able to describe systems with missed
information on their behavior.
2.2 Backward Reachability Analysis
Backward reachability analysis (BRA) theory has
been already used for ordinary Petri nets (Anglano
and Portinale, 1994) and colored Petri nets (Bhan-
dari et al., 2018). BRA on ordinary Petri nets uses
methods such as the reverse of the net, where arcs di-
rections are just reversed (i.e., source becomes target
and target becomes source). However, this method is
disadvantageous for other high level Petri nets like R-
TNCESs. We propose a method that helps to apply
BRA on R-TNCESs and study its benefits comparing
with other existed theories.
Backward reachability analysis (BRA) can be
started from an undesirable state which leads the sys-
tem to a critical behavior, and it highlights all pos-
sible scenarios that cause it. Backward reachability
analysis are widely used in model-based diagnosis
problems. Let (1) S be a system that works incor-
rectly, (2) M
S
be an abstracted model of S, and (3)
OBS =
{
o
1
, o
2
, ..., o
n
}
be a set of states specifying
the observed misbehavior. The model-based diagno-
sis method backtracks the system states according to
its behavior extracted from M
s
, and gives sequences
of initial states that are supposed to be reasons for this
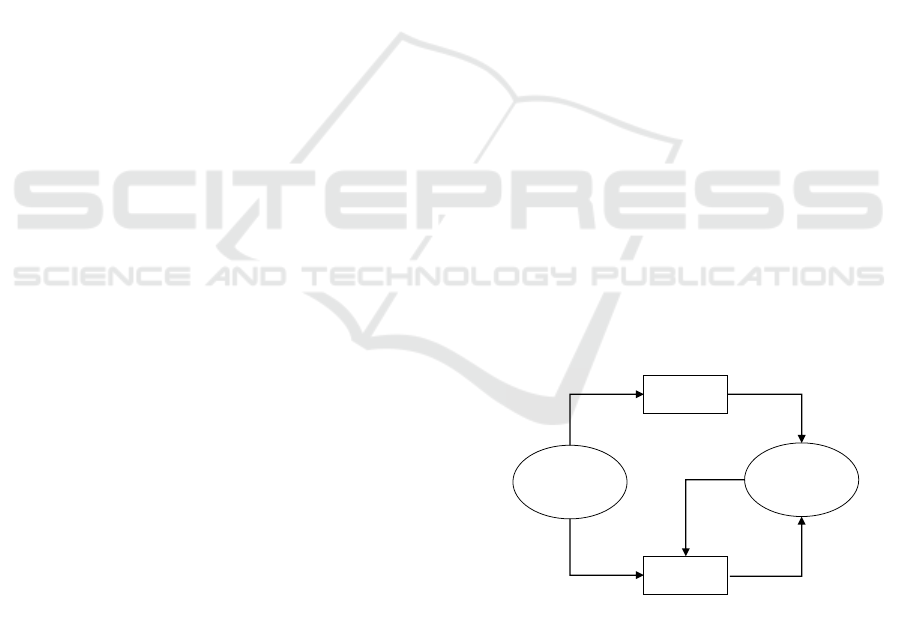
unpredictable misbehavior starting from OBS (Fig.2).
This reasoning is beneficial when we have a non
completed model of system S, i.e., sometimes sys-
tem’s behavior cannot be completely modeled 100%,
thus, some parts are missed such as the initial state
from which a system starts its process. In this case,
model M
S
is built from hardware components data
and their interactions. Using Petri nets formalism,
the missed behavior can be presented as lack of infor-
Semi-behavior
of S
Observation
(Misbehavior)
Explanation of
observation
9 Backtracking the
system
9 Backward
reachability
Model
M
s
Specification
OBS
MBD black box
Faulty
components
Sub-graph of
possible states
Figure 2: Model based diagnosis and backward reachability.
mation about initial marking (i.e., initial state) in the
model. Therefore, M
S
is given as a Petri net model
without initial marking (i.e., non marked Petri net).
Suppose that we aim to explain a misbehavior of such
system using the forward method, then all sequences
with each possible combination of initial marking is
generated. The problem is that in some cases, this rea-
soning costs a lot of extra time due to a huge number
of initial marking possibilities that can even be infinite
and not beneficial for the diagnosis process. Some di-
agnosis works take as an input a system that is mod-
eled using Petri nets like M
s
. Then, backward reach-
ability analysis (BRA) is adopted to generate the sys-
tem’s state space starting from the undesirable state
in OBS. The obtained state space serves to under-
stand possible causes of resulted observations. The
main strength point of this method is that it is able
to have a model M
S
that represents all possible sys-
tems with all combinations of inputs and parameters.
Therefore, each real system of these possible ones in
M
S
is supposed to be diagnosed at the end of the pro-
cess. One of BRA advantages is that it focuses on
critical scenarios rather than all possible ones. Un-
fortunately, it is possible that the graph resulted from
BRA be larger or infinite comparing with the original
one obtained using the forward reachability analysis
(FRA) (Leveson and Stolzy, 1985) for a marked in-
put system. For this case, BRA approach is practical
only if the subsequent graph is smaller than the orig-
inal one obtained by FRA approach. Therefore, gen-
erating backward reachability graphs is infeasible in
some cases like the above one. In the next subsection,
we define what is R-TNCES reverse that will be used
to generate R-TNCES backward reachability graphs.
2.3 Contribution: R-TNCES Reverse
Ordinary Petri nets reversion method can be general-
ized to R-TNCESs by (1) inverting arcs directions in
the nets, and (2) adapting R-TNCESs semantics. The
result is a reversed R-TNCES which is possible to be
ICSOFT 2019 - 14th International Conference on Software Technologies
132

backward analyzed. Adapting R-TNCESs allows to
add necessary procedures related to R-TNCESs se-
mantic in order to complete the reversion and to fa-
cilitate the analysis among resulted structures. The
reversion applied in ordinary Petri nets does not re-
quire adaptations, i.e., a simple reversion of arcs di-
rections is sufficient to perform backward reachabil-
ity. However in R-TNCESs, where the dynamic of
this high level Petri net is different and contains more
constraints, the inversion of arcs directions is not suf-
ficient. We propose some complementary methods to
R-TNCESs reversion method to consider the adapta-
tion of token’s evolution in this special Petri net, e.g.,
cases of, condition/event arcs, reconfigurations,.. etc.
We consider that the reverse of a non marked
R-TNCES RT N(B
RT N
, R
RT N
) is an imaginary non
marked R-TNCES given by
RT N
−1
(B
−1
RT N
, R
−1
RT N
)
where,
• B
−1
RT N
is a set of reversed non marked TNCESs
generated from original non marked TNCESs in
B
RT N
by using arcs inversion generic algorithm
and reversed firing rules as in Table 2,
• R
−1
RT N
is a set of reversed reconfiguration rules that
are generated from original ones in R
RT N
using
Tables 3 and 4.
Table 2: R-TNCESs reversed firing rules.
Arcs RT N RT N
−1
Flow
. . .
. . .
. . .
. . .
Event
. . .
. . .
Condition
. . .
. . .
Table 3: Reconfiguration rules inversion.
r RT N RT N
−1
cond c c
−1
S S S
−1
X T N(
•
r) → T N(r
•
) T N(r
•
) → T N(
•
r)
Table 4: S
−1
: Reversed structure modification instructions.
N° RT N: S RT N
−1
: S
−1
1 Cr(cn(x, y)) De(cn(x, y))
2 Cr(ev(y, y)) De(ev(y, y) )
3 Cr(CC) De(CC)
4 De(cn(x, y)) Cr(cn(x, y))
5 De(ev(y, y) ) Cr(ev(y, y) )
6 De(CC) Cr(CC)
7 Cr(x, m(x)) De(x)
8 Cr(y) De(y)
9
Cr( f a(x, y)) / De( f a(x, y)) /
Cr( f a(y, x)) De( f a(y, x))
10 De(x) Cr(x, 1) or Cr(x, 0)
11 De(y) Cr(y)
12
De( f a(x, y)) / Cr( f a(x, y)) /
De( f a(y, x)) Cr( f a(y, x))
13 Mo(AND(y)) Mo(Or(y))
14 Mo(OR(y)) Mo(And(y))
2.4 Mu Method
As reported in (Hafidi et al., 2018), Mu function im-
proves the generation of accessibility graphs by re-
ducing redundancies and unnecessary computations.
Let RS(B
RS
, R
RS
) be an R-TNCES, where (1) B
RS
=
{
C
1
, ..., C
n
}
is the behavior module containing n > 1
configurations C
1
, .., C
n
, and (2) R
RT N
is the con-
trol module containing k > 1 reconfiguration rules:
r
i j
, 1 ≤ i, j ≤ n that transforms the system from con-
figuration C
i
to configuration C
j
. µ(AG(C
i
), r
i j
) is the
function that takes the accessibility graph of a config-
uration AG(C
i
) and transforms it into another accessi-
bility graph of another configuration AG(C
j
) accord-
ing to the structure-modifications in the applied re-
configuration rule r
i j
, i.e., r
i j
.s is a list containing one
or more structure-modification instructions defined in
Table 1. Function Mu, generates new accessibility
graphs of new configurations from already generated
ones. Rather than computing each graph from zero,
Mu helps to avoid repetitive computation and keep
similar already computed parts of the state space. Mu
function uses a set of rewriting rules on an already
computed graph to transform it to a new graph. Ta-
ble 5 presents some rewriting rules of Mu function.
Other rewriting rules of all possible reconfiguration
scenarios are presented and explained in (Hafidi et al.,
2018). A set of rewriting rules for each possible
structure-modification instruction SMI
m
∈ r
i j
.s, i.e.,
SMI
m
denotes the structure-modification instruction
symbol number m. We denote by (1) a and a
0
: ac-
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs
133
cessibility graph edges, (2) y, y
1
, and y
2
: R-TNCESs
transitions, (3) y
1
v y
2
an event signal from y
1
to y
2
,
(4) enb(s, y) a boolean function that returns 1 if the
transition t is enabled in the state s or 0 otherwise, (5)
src: A → S the function that returns the state repre-
senting the source node of the edge e and tg: A → S
the function that returns the state representing the tar-
get node of the edge e, and (6) SimulateFrom(s) the
function that continues the simulation from a non-
complete graph (i.e., a set of states and a set of edges),
eventual enabled transitions are fired to compute the
additional reachable states on the new structure, start-
ing from the state s.
3 METHODOLOGY
This section presents: our motivation in this paper,
new proposed backward reachability methodology,
algorithm and complexity.
3.1 Motivation
Model-based diagnosis (MBD) of systems (Hamscher
et al., 1992) has attracted many interest since it en-
sures systems safety (Berghout and Bennoui, 2019;
Bennoui et al., 2009; Liu et al., 2016; Bhandari et al.,
2018). Some of diagnosis abilities is explaining the
appearance of an observed system’s misbehavior, de-
termining the faulty components of the system, and
defining what additional information need to be gath-
ered to identify faulty components (De Kleer and
Kurien, 2003). Backward reachability analysis is very
important in model based diagnosis, i.e., it represents
the principal function that backtracks the system pro-
cess. Unfortunately, BRA is a complex function that
is expensive in terms of computing time and memory.
One of BRA high complexity reasons is that it gener-
ates branches of all possible systems. BRA function
is important in complex systems diagnosis and it de-
serves to be improved.
Despite its long success in systems diagnosis,
BRA has a number of problems in use such as
1. Consideration of reconfigurable systems: the pro-
posed algorithms in literature lacks from the con-
sideration of some complex systems like recon-
figurable ones. Contrarily to non-reconfigurable
systems, reconfigurable ones have their own spe-
cial dynamic behavior that needs to be particularly
considered when they are backtracked.
2. Improvement of required time/memory: less re-
search interests focus on optimizing the backward
reachability function. Such an expensive func-
tion needs to include some optimization technique
to improve required time and memory. This is
beneficial because it makes backward reachability
analysis easy and possible for complex systems
such as reconfigurable ones.
Petri nets (Murata, 1989) and their extensions are
ones of the most widely used formalisms (Khawla and
Moln
´
ar, 2018) that have been extensively exploited
for modeling and analyzing concurrent, parallel and
dynamic system. In this paper, we address the prob-
lem of reconfigurable systems backward reachability
using Petri nets extension called R-TNCESs formal-
ism (Zhang et al., 2017b; Zhang et al., 2013; Zhang
et al., 2015; Hafidi et al., 2018).
3.2 Backward Reachability with Mu
Method
In this subsection, we propose a new methodology
for an efficient verification of reconfigurable systems.
Foremost, we use a non marked R-TNCESs formal-
ism for modeling reconfigurable systems. Then, spec-
ify as R-TNCESs states the set of system’s situa-
tion(s) to be checked. Systems situations may rep-
resent undesirable states such as failures, or desirable
ones such as required results. Therefore, situations
are defined according to the problem and the type of
the studied system (i.e., a detailed example that ex-
plains that on Subsection 4.1). The suggested method
in this paper uses the proposed backward reachability
analysis method to generate the backward accessibil-
ity graph of the initial configuration. Then, it uses Mu
method (Hafidi et al., 2018) to improve the computa-
tion of other backward accessibility graphs.
Í
ELs
J
?KJB
E
BRA
Í
ELs
J
)N=LD
E
Mu
?KJB
5
?KJB
Ü
i •
i n
CN=LD
Ü
CN=LD
Ü?5
CN=LD
5
Figure 3: BRA with Mu (the proposed methodology).
The proposed methodology represents a combi-
nation between Mu method and the suggested back-
ward reachability analysis of R-TNCESs to generate
backward reachability graphs. Let us have a reconfig-
urable system with n configurations such that n ∈ N
and n > 1. The proposed method, as depicted in Fig.
3, uses the proposed BRA for R-TNCESs to compute
ICSOFT 2019 - 14th International Conference on Software Technologies
134
Table 5: Mu Rules.
m SMI
m
Rewriting rules on accessibility graphs Comments
(1) Cr(cn(x, y))
a) ∀a ∈ A, Label(a) = y ∧¬enb(src(a), y) ::= a) For each edge labeled
by y: if y is not enabled,
A ← A \
{
a
}
. then delete it.
(2) Cr(ev(y
1
, y
2
))
a) ∀a ∈ A, Label(a) = y
2
::= A ← A \
{
a
}
. a) Delete all edges
labeled by y
2
.
b) ∀a ∈ A, Label(a) = y
1
∧ enb(src(a),y
1
v y
2
)::= b) For each edge
labeled by y
1
, check
A ← A \
{
a
}
∪
{
a
0
}
∧ Label(a
0
) = y
1
v y
2
∧ from its source state if
y
1
v y
2
is enabled, then
src(a
0
) = src(a) ∧tg(a
0
)= src(a)
y
1
vy
2
−→ . delete the edge labeled
by y
1
and add a new
edge labeled
by y
1
v y
2
.
(3) De(cn(x, y)) a) ∀s ∈ S, enb(s, y) ::= SimulateFrom(s).
a) In each state: if y
is enabled, then
continue simulation
from this state.
(4) De(ev(y
1
, y
2
))
a) ∀a ∈ A, Label(a) = (y
1
v y
2
) ::= A ← A \
{
a
}
a) Delete all edges
labeled by y
1
v y
2
.
b) In each state if y
1
b) ∀s ∈ S, enb(s, y
1
) ::= SimulateFrom(s). is enabled, then
continue the simulation
from this state.
c) ∀s ∈ S, enb(s, y
2
) ::= SimulateFrom(s). c) In each state if y
2
is enabled, then
continue the simulation
from this state.
backward accessibility graph graph
1
of initial con-
figuration con f
1
. After that, it employs Mu method
to generate other graphs of the other configurations.
Old methods as explained in Fig. 4 should gener-
ate all graphs using BRA algorithm. Therefore, the
difference between the proposed and the old methods
is that the suggested one generates only one graph.
Other graphs are generated from the initial one, and
then, graph from another until the end of all system’s
configurations. However, in old methods, each graph
is generated independently from others. In addition,
Mu method is used previously in (Hafidi et al., 2018)
with forward reachability analysis methods to gen-
erate forward reachability graphs. However, in this
paper, Mu method is used with the proposed back-
ward reachability analysis method to generate back-
ward reachability graphs. This combination between
both methods allows in one hand to backward ana-
lyze systems under reconfigurability constraints, and
in another hand, to improve time and memory while
generating all the graphs of such complex systems.
Í
ELs
J
?KJB
E
BRA
Í
ELs
J
)N=LD
E
?KJB
Ü
CN=LD
Ü
Figure 4: BRA without Mu (old methods).
3.3 Algorithm and Complexity
Algorithm 1 describes the proposed method of R-
TNCES backward reachability analysis. The al-
gorithm takes as inputs (1) RT a non marked
R-TNCES structure, (2) Con figurations a set of
TNCESs structures describing system’s configura-
tions, (3) Recon figurations a set of Rules describ-
ing system’s transformations, (4) Con f
0
a non marked
TNCES structure describing the initial configuration
of the system, and gives as output Graphs the set of
accessibility graphs of all the system.
Algorithm 1 uses some additional functions (1)
BRA function that takes the initial configuration as in-
put and returns its graph using the backward reach-
ability analysis method described in Subsection.2.2.
(2) AdaptingModel function that adapts RT so that
Mu function, which was proposed for forward analy-
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs
135

sis, can be applied within the current backward analy-
sis. (3) GetGraphsWithMu function that computes
other graphs using Mu. GetGraphsWithMu func-
tion as described in Algorithm 2, takes the same in-
puts as in Algorithm 1, besides the initial accessibility
graph Graph
0
that was already computed using BRA
method. The algorithm uses connections function to
get the set of next reachable configurations from the
graph of the current one. After that it recursively com-
putes each new graph from the previous one and stops
when (1) no next configurations are reachable, i.e.,
SetC = Nil, or (2) the graph is already computed, i.e,
Graph
i
∈ Graphs.
Algorithm 1: GenerateGraphs.
Input: RT (Con figurations : Set of
T NCESs; Recon figurations : Set of
Rules) : R − T NCES; Con f
0
:
T NCES;
Output: Graphs : Set of Accessibility
Graphs;
1 Graph
0
= BRA(Con f
0
);
2 AdaptingModel(RT , Con f
0
, Graph
0
);
3 Graphs = GetGraphsWithMu(RT , Con f
0
,
Graph
0
);
4 Graphs ← Graph
0
∪ Graphs;
Algorithm 2: GetGraphsWithMu.
Input: RT (Con figurations : Set of
T NCESs; recon f igurations : Set of
Rules) : R − T NCES; Con f
0
:
T NCES; Graph
0
: Accessibility
Graph;
Output: Graphs : Set of Accessibility
Graphs;
Variables: SetC: Set of T NCESs;
1 SetC ← connections(Graph
0
);
2 if SetC 6= Nil then
3 foreach Con f
i
∈ SetC do
4 Graph
i
= Mu(con f
i
, con f
0
, Graph
0
);
5 if graph
i
6∈ Graphs then
6 Graphs ← graph
i
∪ Graphs;
7 GetGraphsWithMu(RT , Con f
i
,
Graph
i
);
8 end
9 end
10 end
The time complexity of the entire algorithm: Al-
gorithm 1 in systems with at least 2 configurations is
computed as follows
O(1 ∗ e
m
+ (| Con figurations | −1) ∗ n)
where, (1) O(e
m
) is complexity of the BRA function
used only once for computing the graph of the initial
configuration, and (2) O(n) is complexity of Mu func-
tion (Hafidi et al., 2018) used to compute other acces-
sibility graphs, i.e., (| Con figurations | −1) times in
the worst case when all configurations are reachable.
4 EXPERIMENTATION
This section is composed of two subsections (1) a case
study where paper’s contributions are applied, and (2)
performance evaluation where proposed and related
methodologies are compared using different factors.
4.1 Case Study: FESTO MPS
FESTO MPS is a benchmark production system used
as real case study to apply paper’s contribution.
In next subsections, we first describe FESTO MPS
working process, then, formally model the system us-
ing a non marked R-TNCESs, and finally, verify it
using the proposed method. The same case study was
studied in (Hafidi et al., 2018; Zhang et al., 2013),
however in this paper, for model-based diagnosis pur-
poses, we use the suggested backward reachability
method to generate accessibility graphs rather than
the forward one that was used the previous paper. In
the end of this section, both case studies will be com-
pared to conclude benefits and limits of each method.
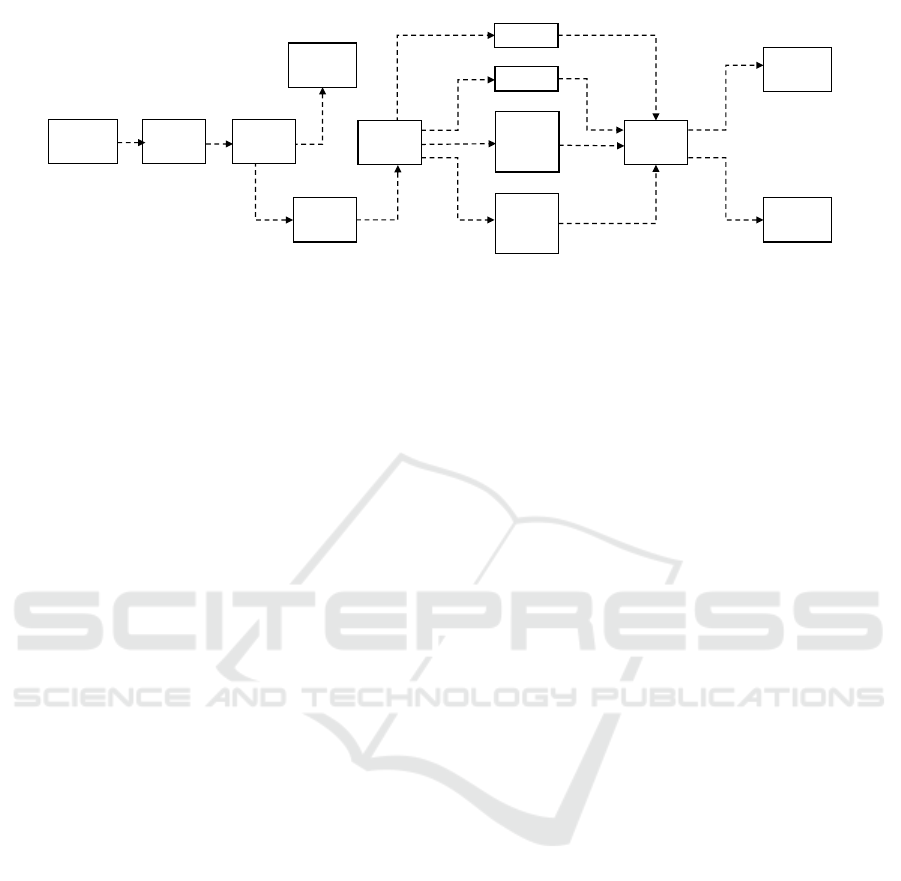
4.1.1 Working Process
FESTO MPS is composed of three main functions:
distributing, testing, and processing peace-works. In
this case study, the system contains two drilling ma-
chines Driller
1
and Driller
2
, and works in three pos-
sible production modes: High, Light
1
, and Light
2
.
First, the system is in High production mode, where
both drilling machines work simultaneously. In some
cases, FESTO MPS changes its behavior and switches
from a mode to another, i.e., when Driller
1
(respec-
tively, Driller
2
) breaks down, the system switches to
Light
2
(respectively, Light
1
) production mode where
only Driller
2
(respectively, Driller
1
) works. This
happens in order to prevent system from malfunctions
when partial hardware failures occur (i.e., a compo-
nent breaks down) or to respond to external instruc-
tions (i.e., user requirements). FESTO MPS main
working process is explained in Fig. 5
ICSOFT 2019 - 14th International Conference on Software Technologies
136
Piece
injection
Convert
Elevate
Evacuate
Driller
1
Test
Driller
1
or
Driller
2
Driller
1
and
Driller
2
Driller
2
Evacuate
Other
station
Rotate
Test
Mdl
1 :
Feeder
Mdl
2 :
Converter
Mdl
3 :
Tester
1
Mdl
4 :
Evacuator
1
Mdl
7
Mdl
6 :
Disc
Mdl
5 :
Elevator
1
Mdl
7
or Mdl
8
Mdl
8
Mdl
9
: Tester
2
Mdl
10
: Evacuator
2
Mdl
7
and Mdl
8
Figure 5: FESTO MPS main process. (Hafidi et al., 2018)
4.1.2 System Encoding
In order to apply formal analysis techniques, it is
necessary to mathematically model the studied sys-
tem FESTO MPS. We model FESTO MPS using R-
TNCES formalism already presented in Subsection
2.1. FESTO MPS is an R-TNCES
FT (B
FT
, R
FT
)
where,
• B
FT
=
{
c
1
, c
2
, c
3
}
: is the behavior mod-
ule that contains all possible configurations,
i.e., FESTO MPS production modes are rep-
resented by R-TNCESs configurations, where
C
1
, C
2
, and C
3
configurations respectively repre-
sent High, Light
1
, and Light
2
production modes.
Each configuration is presented by a set of inter-
connected modules (Mdl
i
) which are control com-
ponents communicating with signals.
• R
FT
=
{
r
c
1
−c
2
, r
c
1
−c
3
, r
c
2
−c
1
, r
c
3
−c
1
}
is the con-
trol module that involves all reconfiguration rules
that transforms the system from a configuration to
another.
The initial configuration c
1
of the studied system is
represented by the TNCES that is graphically shown
in Fig. 6. Other configurations c
2
and c
3
can be
obtained by applying possible reconfiguration rules
from R
FT
.
Considered reconfiguration rules are described as
follows,
• r
c
1
−c
2
= (Driller
2
breaks down;
De(Mdl
8
), De(t
20
), De(p
11
); (p
1
, C
1
) →
(p
1
, C
2
));
• r
c
1
−c
3
= (Driller
1
breaks down;
De(Mdl
7
), De(t
18
), De(p
10
); (p
1
, C
1
) →
(p
1
, C
3
)).
4.1.3 System Verification
We define a set of goal states from which we start
backward reachability: {goal
1
= (S
4
, C
1
), goal
2
=
(S
4
, C
2
)}. goal
1
and goal
2
are undesirable states that
represents tests failure in configurations C
1
and C
2
,
respectively.
We backtrack the system using the proposed R-
TNCESs reverse method, and obtain
FT
−1
(B
−1
FT
, R
−1
FT
)
where,
• B
−1
FT
= {C
−1
1
, C
−1
2
, C
−1
3
}, i.e., obtained using R-
TNCESs reversed firing rules 2 in each configura-
tion,
• R
−1
FT
= {r
−1
c
1
−c
2
, r
−1
c
1
−c
3
, r
−1
c
2
−c
1
, r
−1
c
3
−c
1
}, i.e., ob-
tained using Tables 3 and 3.
The set of considered FT
−1
reconfiguration rules are
described as follows,
• r
−1
c
1
−c
2
= (Driller
2
works;
Cr(Mdl
8
), Cr(t
20
), Cr(p
11
); (p
1
, C
2
) →
(p
1
, C
1
));
• r
−1
c
1
−c
3
= (Driller
1
works;
Cr(Mdl
7
), Cr(t
18
), Cr(p
10
); (p
1
, C
1
) →
(p
1
, C
3
)).
Now, we compute backward reachability graphs
starting from undesirable states goal
1
and goal
2
.
Obtained state space is a set of sub-graphs
{subG(C
1
), subG(C
2
)} from whole system acces-
sibility graphs. sub-graph subG(C
1
) (respectively,
subG(C
2
)) contains branches leading to the undesir-
able state goal
1
(respectively, goal
2
) in C
1
(respec-
tively, C
2
). In real, obtained branches correspond to
the critical executions that the system may pass by
during its working process. The sub-graph subG(C
2
)
is depicted in Fig. 7. The advantage of using back-
ward reachability, is that if focuses on explaining
the appearance of an undesirable behavior goal
1
and
goal
2
, i.e., other behavior of system is not included in
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs
137

the verification. By using the proposed methodology,
we were able to successfully apply backward reach-
ability analysis for the studied reconfigurable system
using R-TNCESs formalism.
Mdl
6
Mdl
5
Mdl
2
Mdl
3
Mdl
4
Mdl
1
Mdl
7
Mdl
8
Mdl
9
Next
station
P
1
P
2
P
3
P
4
P
5
P
6
P
7
P
8 P
9
t
1
t
2
t
3
t
4
t
5
t
7
t
6
t
8
t
9
t
10
t
11
t
12
t
13
t
14
t
15
t
16
t
17
t
18
t
19
t
21
P
12
t
22
t
23
Mdl
10
t
20
P
11
P
10
Figure 6: Initial configuration of FESTO MPS C
1
. (Hafidi
et al., 2018).
S
0
S
1
S
2
S
3
S
4
Figure 7: Backward reachability graph of goal
2
: subG(C
2
).
4.2 Performance Evaluation
In this section, we first study results obtained for the
same case study using different methodologies. Then,
we study the evaluation in large scale systems using
different factors. Finally, we summarize in a compar-
ison table limits and benefits of the proposed method
and previous related ones.
4.2.1 Case Study
In this subsection, we compare obtained results by the
paper’s case study with those of the previous work in
(Hafidi et al., 2018).
We notice that the total number of computed states
is almost the half in current methodology compared
to previous ones. Backward reachability helped to
identify only critical scenarios and their related states
rather than all possible system’s behavior. This can
serve the verification of systems with complex behav-
ior using less time and memory.
Table 6: Number of states current case study VS previous
case study.
Configuration
Number of states
previous current
works work
(Hafidi et al., 2018)
C
1
10 5
C
2
10 5
C
3
10 4
Total 30 14
4.2.2 Number of Computed States vs. Number
of Undesirable States
In this subsection, we apply proposed and related
methodologies in a large scale system using different
number of undesirable states. The curve depicted in
Fig. 8 shows that the number of computed states us-
ing the proposed methodology is less than the number
of states generated using related methodology. In the
best cases, backward reachability generates less states
starting from the undesirable states to the source (pos-
sible initial marking), however, forward methods gen-
erate all possible branches with all possible initial
markings.
5 CONCLUSION
This research work deals with the backward reach-
ability of reconfigurable systems such as reconfig-
urable discrete event control systems RDECSs. The
proposed method allows the applicability of backward
reachability methods on reconfigurable systems mod-
eled by R-TNCESs. The suggested methodology al-
lows to compute backward reachability graphs using
improvement methods that reduce repetitive compu-
tations.
ICSOFT 2019 - 14th International Conference on Software Technologies
138
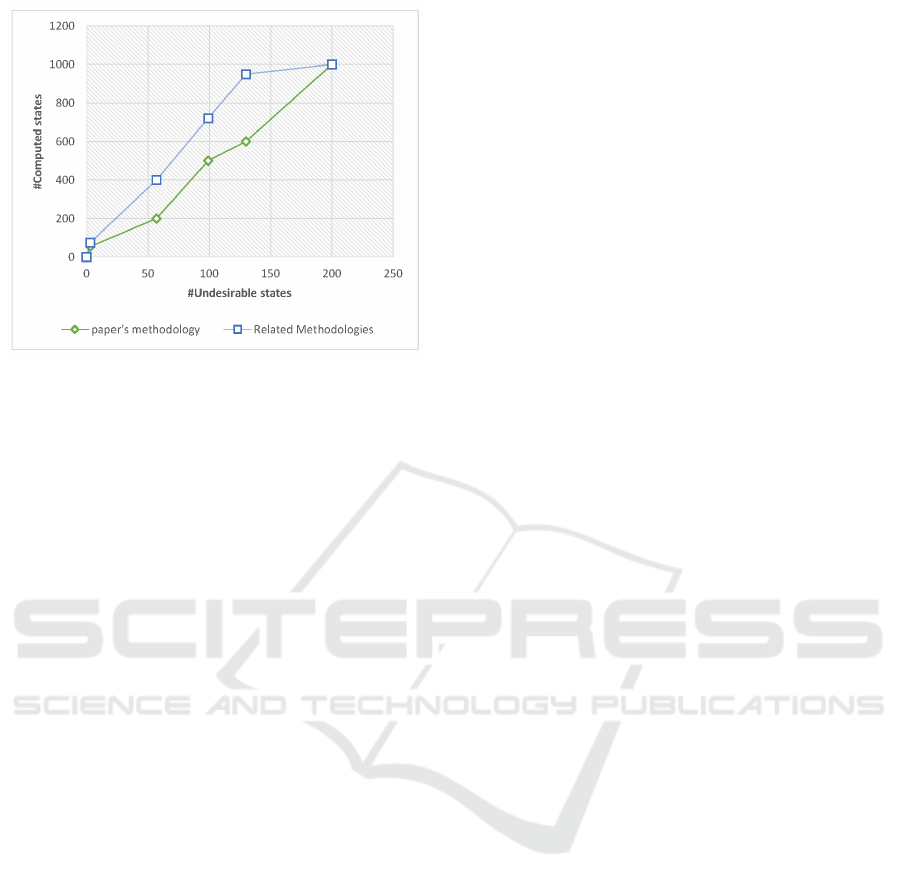
Figure 8: Computed states VS undesirable states.
According to the case study, and performance
evaluation, it is shown that backward reachability be-
comes possible. In addition, the proposed methodol-
ogy for RDECSs improved verification.
Future works will: (1) involve comparison with
tools and methods that use different models, (2) con-
sider probabilistic constraints in computing branches,
and (3) include the proposed improvement method in
a tool in order to automatize it and profit from its gain.
REFERENCES
Aissa, Y. B., Bachir, A., Khalgui, M., Koubaa, A., Li, Z.,
and Qu, T. (2019). On feasibility of multichannel re-
configurable wireless sensor networks under real-time
and energy constraints. IEEE Transactions on Sys-
tems, Man, and Cybernetics: Systems.
Aissa, Y. B., Mosbahi, O., Khalgui, M., and Bachir, A.
(2018). New scheduling mechanism in multi-channel
reconfigurable wsn under qos and energy constraints.
In 32nd annual European Simulation and Modelling
Conference 2018, pages 187–191.
Anglano, C. and Portinale, L. (1994). Bw analysis: a
backward reachability analysis for diagnostic prob-
lem solving suitable to parallel implementation. In
International Conference on Application and Theory
of Petri Nets, pages 39–58. Springer.
Baier, C., Katoen, J., and Larsen, K. (2008). Principles of
Model Checking. MIT Press.
Bennoui, H., Chaoui, A., and Barkaoui, K. (2009). Dis-
tributed causal model-based diagnosis based on inter-
acting behavioral petri nets. pages 99–106.
Berghout, Y. M. and Bennoui, H. (2019). Distributed di-
agnosis based on distributed probability propagation
nets. International Journal of Computational Science
and Engineering, 18(1):72–79.
Bhandari, G. P., Gupta, R., and Upadhyay, S. K. (2018).
Colored petri nets based fault diagnosis in service ori-
ented architecture. International Journal of Web Ser-
vices Research (IJWSR), 15(4):1–28.
Cong, X., Fanti, M. P., Mangini, A. M., and Li, Z. (2017).
Decentralized diagnosis by Petri nets and integer lin-
ear programming. IEEE Transactions on Systems,
Man, and Cybernetics: Systems.
De Kleer, J. and Kurien, J. (2003). Fundamentals of
model-based diagnosis. IFAC Proceedings Volumes,
36(5):25–36.
Dubinin, V., Vyatkin, V., and Hanisch, H.-M. (2015).
Synthesis of safety controllers for distributed au-
tomation systems on the basis of reverse safe
net condition/event systems. In Proc. Trust-
com/BigDataSE/ISPA, volume 3, pages 287–292.
IEEE.
Gharsellaoui, H., Gharbi, A., Khalgui, M., and Ahmed,
S. B. (2012). Feasible automatic reconfigurations of
real-time os tasks. In Handbook of Research on Indus-
trial Informatics and Manufacturing Intelligence: In-
novations and Solutions, pages 390–414. IGI Global.
Ghribi, I., Abdallah, R. B., Khalgui, M., Li, Z., Alnowi-
bet, K., and Platzner, M. (2018). R-codesign: Code-
sign methodology for real-time reconfigurable embed-
ded systems under energy constraints. IEEE Access,
6:14078–14092.
Hafidi, Y., Kahloul, L., Khalgui, M., Li, Z., Alnowibet, K.,
and Qu, T. (2018). On methodology for the verifica-
tion of reconfigurable timed net condition/event sys-
tems. IEEE Transactions on Systems, Man, and Cy-
bernetics: Systems, (99):1–15.
Hafidi., Y., Kahloul., L., Khalgui., M., and Ramdani., M.
(2019). On improved verification of reconfigurable
real-time systems. In Proceedings of the 14th Interna-
tional Conference on Evaluation of Novel Approaches
to Software Engineering - Volume 1: ENASE,, pages
394–401. INSTICC, SciTePress.
Hamscher, W., Console, L., and de Kleer, J., editors (1992).
Readings in Model-based Diagnosis. Morgan Kauf-
mann Publishers Inc., San Francisco, CA, USA.
Khalgui, M. and Mosbahi, O. (2010). Intelligent distributed
control systems. Information and Software Technol-
ogy, 52(12):1259–1271.
Khalgui, M., Mosbahi, O., Li, Z., and Hanisch, H. M.
(2011). Reconfigurable multiagent embedded control
systems: From modeling to implementation. IEEE
Transactions on Computers, 60(4):538–551.
Khalgui, M., Rebeuf, X., and Simonot-Lion, F. (2004). A
behavior model for iec 61499 function blocks. In Pro-
ceedings of the 3rd Workshop on Modelling of Ob-
jects, Components, and Agents, pages 71–88.
Khalgui, M., Rebeuf, X., and Simonot-Lion, F. (2007). A
deployment method of component based applications
on distributed industrial control systems. European
Jounal of Automated Systems, 41(6):707–732.
Khawla, B. and Moln
´
ar, B. (2018). An fsm approach for hy-
pergraph extraction based on business process model-
ing. In International Conference on Computer Science
and its Applications, pages 158–168. Springer.
Koszewnik, A., Nartowicz, T., and Pawluszewicz, E.
(2016). Fractional order controller to control pump
New Methodology for Backward Analysis of Reconfigurable Event Control Systems using R-TNCESs
139

in FESTO MPS PA compact workstation. In Proc.
17th International Carpathian Control Conference
(ICCC), pages 364–367.
Lakhdhar, W., Mzid, R., Khalgui, M., Li, Z., Frey, G., and
Al-Ahmari, A. (2018). Multiobjective optimization
approach for a portable development of reconfigurable
real-time systems: From specification to implementa-
tion. IEEE Transactions on Systems, Man, and Cyber-
netics: Systems.
Leveson, N. G. and Stolzy, J. L. (1985). Analyzing safety
and fault tolerance using time petri nets. In Inter-
national Joint Conference on Theory and Practice of
Software Development, pages 339–355. Springer.
Liu, B., Ghazel, M., and Toguy
´
eni, A. (2016). Model-
based diagnosis of multi-track level crossing plants.
IEEE Transactions on Intelligent Transportation Sys-
tems, 17(2):546–556.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Naidji, I., Smida, M. B., Khalgui, M., and Bachir, A.
(2018). Non cooperative game theoretic approach
for residential energy management in smart grid. In
The 32nd Annual European Simulation and Modelling
Conference, pages 164–170, Ghent, Belgium.
P
´
ozna, A. I., Gerzson, M., Leitold, A., and Hangos, K.
(2016). Colored petri net based diagnosis of process
systems.
Qin, M., Li, Z., Zhou, M., Khalgui, M., and Mos-
bahi, O. (2012). Deadlock prevention for a class of
petri nets with uncontrollable and unobservable tran-
sitions. IEEE Transactions on Systems, Man, and
Cybernetics-Part A: Systems and Humans, 42(3):727–
738.
Ramdani, M., Kahloul, L., and Khalgui, M. (2018). Au-
tomatic properties classification approach for guiding
the verification of complex reconfigurable systems. In
Proc. Proceedings of the 13th International Confer-
ence on Software Technologies - Volume 1: ICSOFT,,
pages 591–598. INSTICC, SciTePress.
Ramdani., M., Kahloul., L., Khalgui., M., and Hafidi., Y.
(2019). R-tnces rebuilding: A new method of ctl
model update for reconfigurable systems. In Proceed-
ings of the 14th International Conference on Eval-
uation of Novel Approaches to Software Engineer-
ing - Volume 1: ENASE,, pages 159–168. INSTICC,
SciTePress.
Wang, X., Khalgui, M., and Li, Z. (2011). Dynamic low
power reconfigurations of real-time embedded sys-
tems. In PECCS, pages 415–420.
Zhang, J., Frey, G., Al-Ahmari, A., Qu, T., Wu, N., and Li,
Z. (2017a). Analysis and control of dynamic recon-
figuration processes of manufacturing systems. IEEE
Access.
Zhang, J., Khalgui, M., Li, Z., Frey, G., Mosbahi, O.,
and Salah, H. B. (2015). Reconfigurable coordination
of distributed discrete event control systems. IEEE
Trans. Contr. Sys. Techn., 23(1):323–330.
Zhang, J., Khalgui, M., Li, Z., Mosbahi, O., and Al-Ahmari,
A. (2013). R-TNCES: A novel formalism for recon-
figurable discrete event control systems. IEEE Trans.
Systems, Man, and Cybernetics: Systems, 43(4):757–
772.
Zhang, S., Wu, N., Li, Z., Qu, T., and Li, C. (2017b). Petri
net-based approach to short-term scheduling of crude
oil operations with less tank requirement. Information
Sciences, 417:247–261.
ICSOFT 2019 - 14th International Conference on Software Technologies
140
