Vision-based Localization of a Wheeled Mobile Robot with a Stereo

Camera on a Pan-tilt Unit

A. Zde

sar

, G. Klan

car

and I.

Skrjanc

University of Ljubljana, Faculty of Electrical Engineering, Tr

ska 25, 1000 Ljubljana, Slovenia

Keywords:

Mobile Robots, Robot Vision, Optimal Filtering, Estimation Algorithms, Localization, System Observability.

Abstract:

This paper is about a vision-based localization of a wheeled mobile robot (WMR) in an environment that

contains multiple artiﬁcial landmarks, which are sparsely scattered and at known locations. The WMR is

equipped with an on-board stereo camera that can detect the positions and IDs of the landmarks in the stereo

image pair. The stereo camera is mounted on a pan-tilt unit that enables rotation of the camera with respect to

the mobile robot. The paper presents an approach for calibration of the stereo camera on a pan-tilt unit based

on observation of the scene from different views. Calibrated model of the system and the noise model are then

used in the extended Kalman ﬁlter that estimates the mobile robot pose based on wheel odometry and stereo

camera measurements of the landmarks. We assume that the mobile robot drives on a ﬂat surface. In order to

enforce this constraint, we transform the localization problem to a two-dimensional space. A short analysis

of system observability based on indistinguishable states is also given. The presented models and algorithms

were veriﬁed and validated in simulation environment.

1 INTRODUCTION

Autonomous mobile robots are one of the emerging

ﬁelds of technology that is not only expected to be-

come an inevitable part of smart factories of tomor-

row but will play an essential role in our cities and

homes of the future. Advances in the development

of intelligent and autonomous systems are paving the

way to a new breed of robotic systems that will be able

to work alongside humans in a non-intrusive, harm-

less and cooperative way. Nowadays, the self-driving

vehicles are being tested on roads in various trafﬁc

conditions daily and some self-driving technologies

are already implemented in the most modern con-

sumer vehicles.

Autonomous mobile systems perceive the envi-

ronment through sensors. Commonly used sensors

in mobile robotics are proximity and distance sensors

(e.g. ultrasonic distance sensors, laser range scan-

ners, etc.) that enable detection of obstacles, map

building and localization. The emergence of new sen-

sor technologies and contemporary computational ca-

pabilities broaden the range of available sensors that

https://orcid.org/0000-0002-2254-6069

https://orcid.org/0000-0002-1461-3321

https://orcid.org/0000-0002-0502-5376

are appropriate for environment perception. Cameras

are one of the most promising sensors in the ﬁeld of

mobile robotics and they are seldom used to solve

the mobile robot localization and mapping problems

(Se et al., 2001; Agrawal and Konolige, 2006; Du

and Tan, 2016; Fischer et al., 2016; Piasco et al.,

2016; Fuentes-Pacheco et al., 2015; Konolige and

Agrawal, 2008; Mei et al., 2011). The vision-based

environment mapping and localization problems are

commonly solved in the framework of Kalman ﬁlter

(Chen, 2012) or particle ﬁlter (Kim et al., 2017; Del-

laert et al., 1999).

In this paper a stereo camera is used as a sensor

for localization of a wheeled mobile robot (WMR).

The environment is sparsely scattered with artiﬁcial

landmarks at known locations that can be robustly de-

tected in each image of the stereo camera whenever

they are visible in the camera ﬁeld of view. In our case

we use square-based markers that can be detected ef-

ﬁciently with the ArUco image processing approach

(Garrido-Jurado et al., 2016). In order to extend

the tracking range of landmarks, even when the mo-

bile robot moves around the environment, the stereo

camera is mounted on a Pan-Tilt Unit (PTU) that

enables rotation of the camera around its vertical and

544

Zdešar, A., Klan

car, G. and Škrjanc, I.

Vision-based Localization of a Wheeled Mobile Robot with a Stereo Camera on a Pan-tilt Unit.

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 544-551

ISBN: 978-989-758-380-3

horizontal axis. This paper presents the models and

algorithm for localization of the WMR that drives on

a ﬂat ground and observes the landmarks with a stereo

camera. This is a reasonable assumption for many

WMRs in indoor environment, and since we take this

assumption implicitly into the model a better perfor-

mance of the pose estimation can be expected. The

presented approach is therefore not suitable for legged

robots and robots that operate on uneven terrain.

The rest of the paper is structured as follows. In

Section 2 a detailed description of the system is given,

along with mathematical model of the system and cal-

ibration procedure for estimation of the parameters

that describe the static transformation of the stereo

camera on the PTU. Section 3 is about mobile robot

localization, and it presents the stochastic modelling

of the system for the purpose of localization, analysis

of the system observability and localization approach.

In Section 4 some conclusions are drawn.

2 SYSTEM DESCRIPTION

The system is shown in Fig. 1. On the WMR Pioneer

3-AT a PTU with a stereo camera is mounted. The

mobile system is also equipped with other proximity

and distance sensors, but these are not considered in

this work.

Figure 1: WMR Pioneer 3-AT with a stereo camera on a

PTU.

Let us introduce the coordinate frames that we

use: world frame W ; robot frame R (origin is in the

intersection of the robot vertical rotation axis and the

ground plane); base frame S, pan frame U and tilt

frame V of the PTU; left (right) camera frame C

);

stereo camera frame C (between the left and right

camera frame); left (right) image frame P

). The

transformations between the frames are represented

graphically in Fig. 2.

Static transformation that describes the pose of the

Mobile

robot

Stereo

camera

Pan-tilt

unit

World W

Robot R

Pan-tilt S

Pan U

Tilt V

Stereo camera C

Left camera C

Left image P

Right camera C

Right image P

, t

= Rot

(ψ), t

= 0

= Rot

(θ), t

= 0

, t

Figure 2: Diagram of the static (solid arrows) and dynamic

(curly arrows) transformations between the frames.

PTU on the mobile robot is:

= I , t



0.154 0.023 0.563



, (1)

where I is an identity matrix.

The frames S, U and V have a common origin (in

the intersection of the pan and tilt rotation axes):

= t

= 0 ,

where 0 is the vector of zeros. Orientations of the

frames U and V , which are dependent on the pan and

tilt angles, ψ and θ, are given in (2) and (3).

= Rot

(ψ) =





cosψ −sinψ 0

sinψ cosψ 0

0 0 1





(2)

= Rot

(θ) =





cosθ 0 sinθ

0 1 0

−sin θ 0 cosθ





(3)

Notation Rot

(α) represents a rotation around the axis

a for the angle α.

In (4) the static transformations of the cameras

with respect to the tip of the PTU (tilt frame V ) are

given.

= R

= Rot

(−

)Rot

(−

)



0.002 0.032 0.057





0.002 −0.032 0.057



(4)

The values in (1) and (4) have been obtained using

the calibration procedure described in Section 2.1.

Vision-based Localization of a Wheeled Mobile Robot with a Stereo Camera on a Pan-tilt Unit

545

2.1 System Calibration

The intrinsic parameters (P

and P

) and the rel-

ative pose between the cameras (R

and t

) in

the stereo-camera setup can be determined using the

stereo camera calibration procedure (Bouguet, 2004).

Several images of the chessboard-like pattern from

different poses need to be captured. The pattern need

to be visible in both images. From the corresponding

points in the stereo image pairs and given the known

size of the pattern square, the stereo-camera parame-

ters can be obtained. If required, the calibration pro-

cedure can be extended in a way that lens distortions

are taken into account.

In our case we also need to determine the relative

pose of the stereo camera with respect to the tip of the

PTU, i.e. R

and t

. The relative pose of the stereo

camera with respect to the tip of the PTU could be

measured, but since the location of the camera frame

origin and also the location of the tip of the PTU are

not directly accessible, this is hard to do without an

error. Therefore we would like to estimate this pose

with an appropriate calibration procedure that is de-

scribed next.

Given a calibrated stereo camera we observe a set

of points on a static object in the environment (with

respect to the base frame of the PTU) from different

conﬁgurations (views) of the PTU. In the i-th conﬁg-

uration the pose of the tip with respect to the base of

the PTU is represented with rotation R

V,i

(the pan an-

gle is ψ

and the tilt angle is θ

). The triangulation

approach can be used to estimate the 3D positions (in

the stereo camera frame) p

C,i,l

, l = 1, 2, . . . , n, of the

observed n image points. Observing the same set of

points from m different views (conﬁgurations of the

PTU), the transformations R

C,0

C, j

, t

C,0

C, j

, j = 1, 2, . . . , m,

can be obtained from the set of points in views i = 0

and i = j in the following way. First the centres of the

points

C,i

∑

k=1

C,i,k

are evaluated for each view

i, and each set of the points is given with respect to its

centre:

C,i,k

= p

C,i,k

−

C,i

, (5)

for every point k in every view i. The rigid transfor-

mation p

C,0,k

= R

C,0

C, j

C, j,k

+ t

C,0

C, j

can be determined

with the minimization of the least squares error cost

function J:

J =

∑

k=1



C,0,k

− R

C,0

C, j

C, j,k

− t

C,0

C, j



. (6)

Taking into account the centred set of points (5), the

criterion (6) can be written as:

J =

∑

k=1



C,0,k

− R

C,0

C, j

C, j,k



, (7)

since

C,0

−R

C,0

C, j

−t

C,0

C, j

= 0. The cost function (7)

has minimum where the trace(R

C,0

C, j

) has maximum

(Eggert et al., 1997), and H

is deﬁned as:

∑

k=1

C, j,k

C,0,k

Rotation R

C,0

C, j

that maximizes the aforementioned

trace can be obtained from the Singular Value Decom-

position (SVD) of H

= U

C,0

C, j

= V

If the determinant detR

C,0

C, j

is −1 instead of +1, the

transformation represents a reﬂection rather than ro-

tation. In such a case the rotation can be determined

from R

C,0

C, j

= [v

j,1

, v

j,2

, −v

j,3

, where the columns

are obtained from the matrix V

= [v

j,1

, v

j,2

, v

j,3

Once the rotation is known, the translation vector t

C,0

C, j

can be estimated from:

C,0

C, j

C,0

− R

C,0

C, j

More closed-form approaches that can be used to

solve the presented rigid-motion estimation problem

can be found in (Eggert et al., 1997).

The orientation of the PTU tip in the view j =

1, 2, . . . , m with respect to the view i = 0 is R

V,0

V, j

V,0

V, j

. The static orientation R

that is view in-

variant can be obtained from the set of relations ( j =

1, 2, . . . , m):

V,0

V, j

= R

C,0

C, j

. (8)

At least two sets of (8) are required to estimate R

therefore the pattern of points need to be observed

from at least three different conﬁgurations of the

PTU. The system of equations (8) can be written as:



V,0

V, j

⊗ R

C,0

C, j

− I



vec





= 0 , (9)

where operator ⊗ represents the Kronecker matrix

product and vec(X) is a vector with stacked columns

of the matrix X. Several different pairs of matrices

V,0

V, j

and R

C,0

C, j

can therefore be stacked together into

the linear form (9) that can be solved using the SVD

algorithm. Once the estimate of the rotation R

obtained, the translation vector t

can be determined

from the linear system of equations:



V,0

V, j

− I



= R

C,0

− R

V,0

V, j

C, j

. (10)

At least two systems like (10) need to be stacked to-

gether in order to solve for the translation vector t

With an appropriate modiﬁcation, the presented

calibration procedure can also be used to determine

the static rotation R

and translation t

if the pose of

the mobile robot in the world coordinate frame can be

measured.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

546

3 LOCALIZATION

The problem of localization is about estimation of

the transformation between the world and robot frame

and t

in Fig. 2). In our case we would like to

achieve this based on fusion of wheel odometry and

measurement of multiple landmarks at known loca-

tions with a stereo camera. If the WMR motion is

constrained to the ground plane, the pose of the robot

with respect to the world can be given with the gener-

alized coordinates q

(k) = [x(k) y(k) ϕ(k)]:





cosϕ(k) −sin ϕ(k) 0

sinϕ(k) cosϕ(k) 0

0 0 1





, t





x(k)

y(k)





where the coordinates x(k) and y(k) represent po-

sition and the coordinate φ(k) is orientation of the

robot. This is a reasonable assumption for many in-

door spaces since we assume that the mobile system

drives on a ﬂat surface and that it does not tilt sig-

niﬁcantly. We also assume that the poses of all the

static and also moving sensors on-board of the mobile

system are known at all times. This means that both

states of the PTU are measurable. All the static trans-

formations can be determined with the procedure pre-

sented in the previous section. In the following sub-

section the modelling of the system with uncertainties

is presented that takes into account different simpli-

ﬁcations. Since the mobile robot only moves along

the ground plane, the estimation problem is also con-

verted to a pure 2D estimation problem. In this paper

we also assume that the PTU is not moving during the

localization, i. e. the PTU is in its home position all

the time.

3.1 System Modelling

3.1.1 Wheeled Mobile Robot

The WMR has a differential drive (the wheels on each

side are driven jointly). The kinematic model of the

differential drive in the discrete form with the sam-

pling time T can be written as:

q(k + 1) = q(k) +





T v(k)cosϕ(k)

T v(k)sinϕ(k)

T ω(k)





where v(k) and ω(k) are the WMR linear and angular

velocity, respectively.

Wheels on each side of the mobile robot are

equipped with incremental encoders, therefore the

odometry can be implemented. Given the true relative

encoder readings between one sample time for the left

and right wheel u

(k) = [∆λ

(k) ∆λ

(k)], we assume

the following odometry model in the discrete form:

q(k + 1) = q(k) + g







∆λ

(k)+w

(k)+∆λ

(k)+w

(k)

cosϕ(k)

∆λ

(k)+w

(k)+∆λ

(k)+w

(k)

sinϕ(k)

∆λ

(k)+w

(k)−∆λ

(k)−w

(k)







(11)

where g

is the constant that converts the encoder

readings into relative distances and L is the distance

between the wheels — both parameters are normally

determined with calibration. The encoder readings

include a normally distributed white noise w(k) =

(k) w

(k)] with zero mean. The covariance of

the noise w(k) is assumed to be increasing with the

magnitude of the encoder reading, which coincides

with the speed of the wheels, according to the model

(Tesli

c et al., 2011):

(k) =



∆λ

(k)σ

0 ∆λ

(k)σ



3.1.2 Stereo Camera

We assume that we have a calibrated stereo camera

system in canonical conﬁguration with the baseline

distance B and focal length of each camera f . The

origin of each camera image plane coincides with the

camera optical center and the axis x of the left im-

age frame is colinear with the axis x in the right im-

age frame. The projections of a single point in the

3-D space to the left and right camera image plane

are (x

, y

) and (x

, y

), respectively. Since the posi-

tions of landmarks are measured in each image with

a marker detection algorithm (Garrido-Jurado et al.,

2016), let us assume that the aforementioned variables

have normal distribution. They can be gathered in a

vector s:

s =





∈ N (

s, Q

), (12)

where

s is the expected value of the measurement vec-

tor s and Q

is the measurement noise covariance ma-

trix. The shape of the covariance matrix Q

is as-

sumed to be block diagonal, since the measurement

noises of the left and right camera are independent

of each other (shaking of the stereo camera rig is not

considered here):







0 0

0 0 σ







. (13)

In (13) the diagonal elements represent the variances

and the off-diagonal elements are the covariances.

Let us represent the position of a point in the 3D

camera frame. The origin of the stereo camera frame

Vision-based Localization of a Wheeled Mobile Robot with a Stereo Camera on a Pan-tilt Unit

547

C is in the middle of the line that connects the cam-

era focal points, z

-axis is perpendicular to the image

plane and it is pointing outwards to the scene, y

-axis

is parallel to the vertical image axis and x

-axis is

parallel to the horizontal image axis, pointing in the

direction that makes the camera frame right handed.

Here we introduce a special coordinate vector r for

presentation of the point in the stereo camera frame:



tanα tan β z







. (14)

This representation can uniquely represent only the

half-space in front of the camera (z

> 0) and it is

therefore suitable only for the cameras that have the

ﬁeld-of-view smaller that π.

The position of the point r in the camera frame can

be determined from the projection vector (12) using

triangulation:

2 f

B f

−x

The variance of this estimate is therefore:







+σ

4 f

+σ

4 f

−z

−σ

2B f

+σ

4 f

+σ

4 f

−z

−σ

2B f

−z

−σ

2B f

−z

−σ

2B f

+σ







If we assume that the measurement noises of the

left and right camera have the same properties, the

following equivalence of variances and covariances

holds: σ

= σ

and σ

= σ

; and the covari-

ance matrix Q

becomes block diagonal. If we fur-

ther assume that the covariances are zero (σ

= 0), the covariance matrix Q

becomes diag-

onal, where the diagonal elements are:

tanα

tanβ

2 f

2σ

. (15)

From (14) the position of the point in the stereo

camera frame p

can be obtained:







tanα z

tanβ z



Under the assumption (15), the measurement covari-

ance matrix Q

of the vector p

in the stereo camera

frame is:





tanα

+ (tan α)

tanαtanβσ

tanασ

tanαtanβσ

tanβ

+ (tan β)

tanβσ

tanασ

tanβσ





(16)

The transformation of the point p

in the stereo

camera frame to the point p

in the mobile robot base

frame is p

= R

+ t

as deﬁned in Section 2. The

covariance (16) can also be transformed to the mobile

robot base frame:

= R

)

Since we are dealing with estimation of the mobile

robot that can only move in the ground plane, we can

make the projection of the 3D points to the ground

plane (z

= 0), i.e. the point in the 2D ground plane

is therefore p

= P

, where P

is the parallel pro-

jection matrix:



1 0 0

0 1 0



The covariance matrix Q

that is the projection of the

covariance matrix Q

can be given as:

= P

)

. (17)

In the conﬁguration when the stereo camera is in

its home position, in which case the camera axis z

aligned with the robot axis x

and the camera axis x

is in the opposite direction of the robot axis x

, the p

simpliﬁes to:

B f

−x

+ x

−

−x

+ y

, (18)

where x

and y

are the ﬁrst and the second element

of the translation vector t

, respectively. The covari-

ance matrix (17) in this particular case is:



−tan ασ

tanα

+ (tan α)



. (19)

The covariance matrix (19) is strongly dependent on

the distance to the measured point due to the fact

that σ

∝ z

. Top row in Figure 3 shows covari-

ances (19) as ellipses for different positions of the

landmarks overlayed over simulated noisy data. The

proposed noise model was veriﬁed with real measure-

ments (bottom row in Figure 3) by temporal observa-

tion of landmarks at various positions from a static

WMR.

The (18) represents the measurement of the point

in the ground plane. This measurement can also be

given in polar coordinates z

= [d θ]:

+ y

arctan

+ jπ

, j ∈ {0, 1}.

The stereo camera sensor can therefore be considered

as the sensor that measures the distance and angle to

the landmark. In our case we considered that the vi-

sion system can also determine the ID of the measured

landmark, therefore we can distinguish between dif-

ferent landmarks. Let us express the measurement of

the landmark with the system state vector q(k):

z(k) =



d(k)

θ(k)



− x(k))

+ (y

− y(k))

arctan

−y(k)

−x(k)

− ϕ(k) + j(k)π

(20)

where x

and y

are the coordinates of the landmark

in the world frame.

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

548

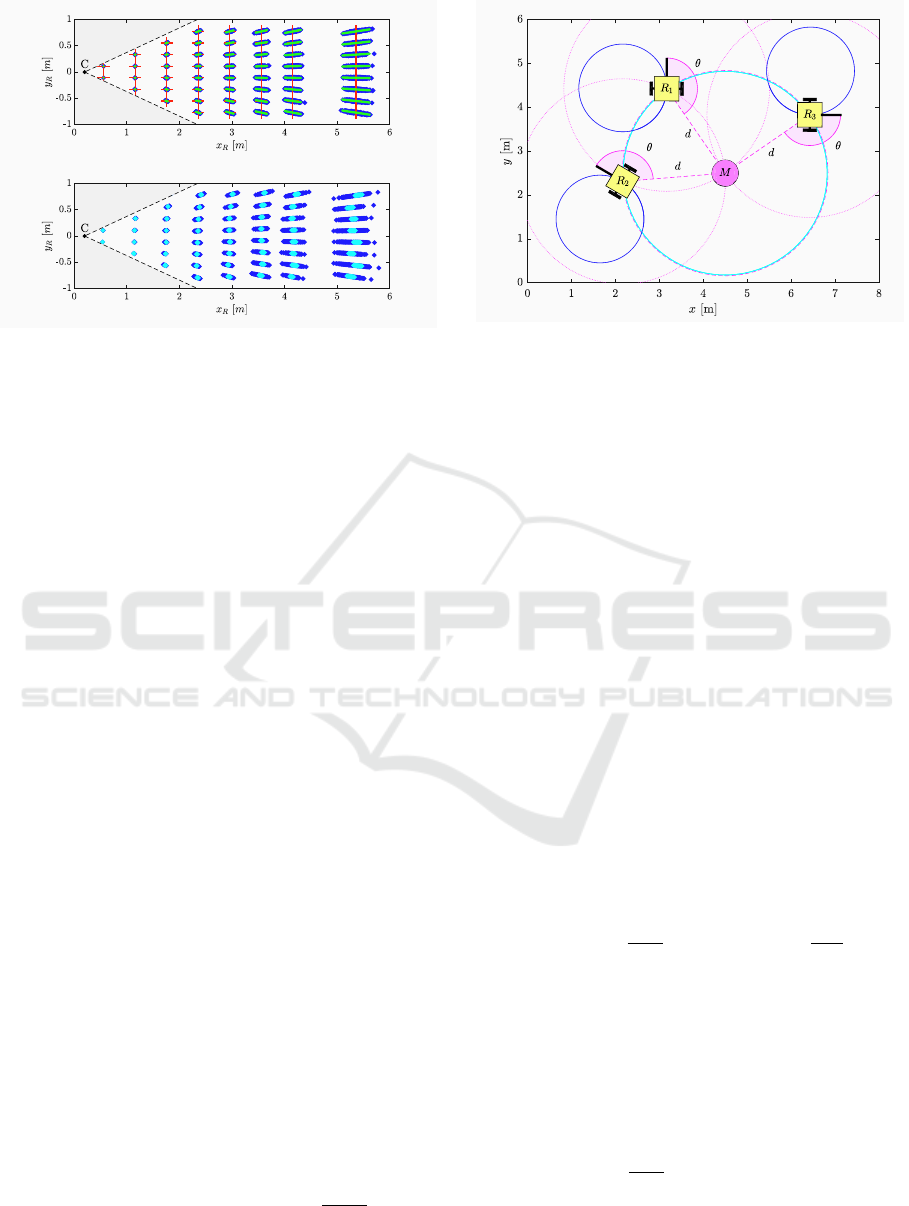
Figure 3: Top, simulation of the stereo camera measurement

noise for multiple landmarks that are in the stereo camera C

ﬁeld of view (red cross – real landmark position, blue – sim-

ulated noise, green – noise covariance ellipse). Bottom, real

measurements (cyan – static camera, blue – small shaking

of the camera).

3.2 System Observability

In order to estimate system states they need to be ob-

servable. The observability of the non-linear system

can be evaluated based on the analysis of indistin-

guishable states. Brieﬂy, two states are indistinguish-

able if for every input on a ﬁnite time interval, identi-

cal outputs are obtained. A system is observable if the

set of all the indistinguishable states of a state x con-

tains only the state x for every state x in the domain of

deﬁnition. For more detailed deﬁnition see (Hermann

and Krener, 1977).

Let us evaluate the observability of the system in

the case of only one landmark graphically. In Fig-

ure 4 we can see three robots in different poses that

all measured the same distance and angle to the land-

mark. Even if the robots move along any admissi-

ble trajectory (e.g. along the circle) there is no way

to distinguish between different robot poses based on

measured outputs. The pose of the robot q is clearly

not observable if only a single landmark is used. In a

similar way it is not hard to observe that the system is

observable if two or more landmarks are used, since

we have assumed that the IDs of the landmarks are

also known. If the later would not hold, three or more

landmarks would be required.

Now we introduce a new state vector q

(k) =

[d(k) θ(k)] that has all the states measurable directly.

The kinematic model of this system is:

(k + 1) = q

(k) +

−T v(k)cosθ(k)

T ω(k) + T v(k)

sinθ(k)

d(k)

. (21)

The system (21) gives only a partial information about

Figure 4: Three poses of the robots that are indistinguish-

able from the outputs in the case of a single landmark M.

the system pose (a subspace of possible robot poses),

but the system is completely observable already in the

case of a single landmark.

3.3 Extended Kalman Filter

We use Extended Kalman Filter (EKF) to solve the lo-

calization problem, which consists of a prediction and

a correction step. The pose of the mobile robot q(k)

could be estimated directly, if the model (11) would

be used in the prediction step of the EKF and the cor-

rection step would be made based on the measure-

ments (20) to all the visible landmarks.

In this paper we used a different approach, us-

ing multiple partial estimators that estimate the states

p,m

(k) for each visible landmark m independently.

Each partial estimator uses the model (21) in the pre-

diction step of the EKF:

p,m

(k + 1) = f

p,m

(k), u(k)),

p,m

(k + 1) = A

p,m

(k)P

p,m

(k)A

p,m

(k)+

+ F

p,m

(k)Q

p,m

(k)F

p,m

(k) ,

where A

p,m

(k) =

∂f

p,m

∂q

p,m



and F

p,m

(k) =

∂f

p,m

∂w



. The

measurement (20) of the associated landmark is then

used in the correction of each partial estimator:

p,m

(k) = C

p,m

(k)

p,m

(k)C

p,m

(k) + R

p,m

(k)

p,m

(k) =

p,m

(k)C

p,m

(k)L

−1

p,m

(k)

p,m

(k) =

p,m

(k) + K

p,m

(k)(z

p,m

(k) −

p,m

(k)) ,

p,m

(k) =

p,m

(k) − K

p,m

(k)C

p,m

(k)

p,m

(k) ,

where C

p,m

(k) =

∂h

p,m

∂q

p,m



. The Q

p,m

(k) and R

p,m

(k)

in the EKF are deﬁned according to the covariance

model developed in Section 3.1. In this way we do

not estimate the pose of the mobile robot, but only the

Vision-based Localization of a Wheeled Mobile Robot with a Stereo Camera on a Pan-tilt Unit

549

distances and headings of each landmark with respect

to the WMR. The estimates q

p,m

(k), m = 1, 2, . . . , M

are then merged into the estimate of the state q(k).

This can be achieved using a triangulation (or trilater-

ation) approach, e.g. using the approach presented in

(Betke and Gurvits, 1997).

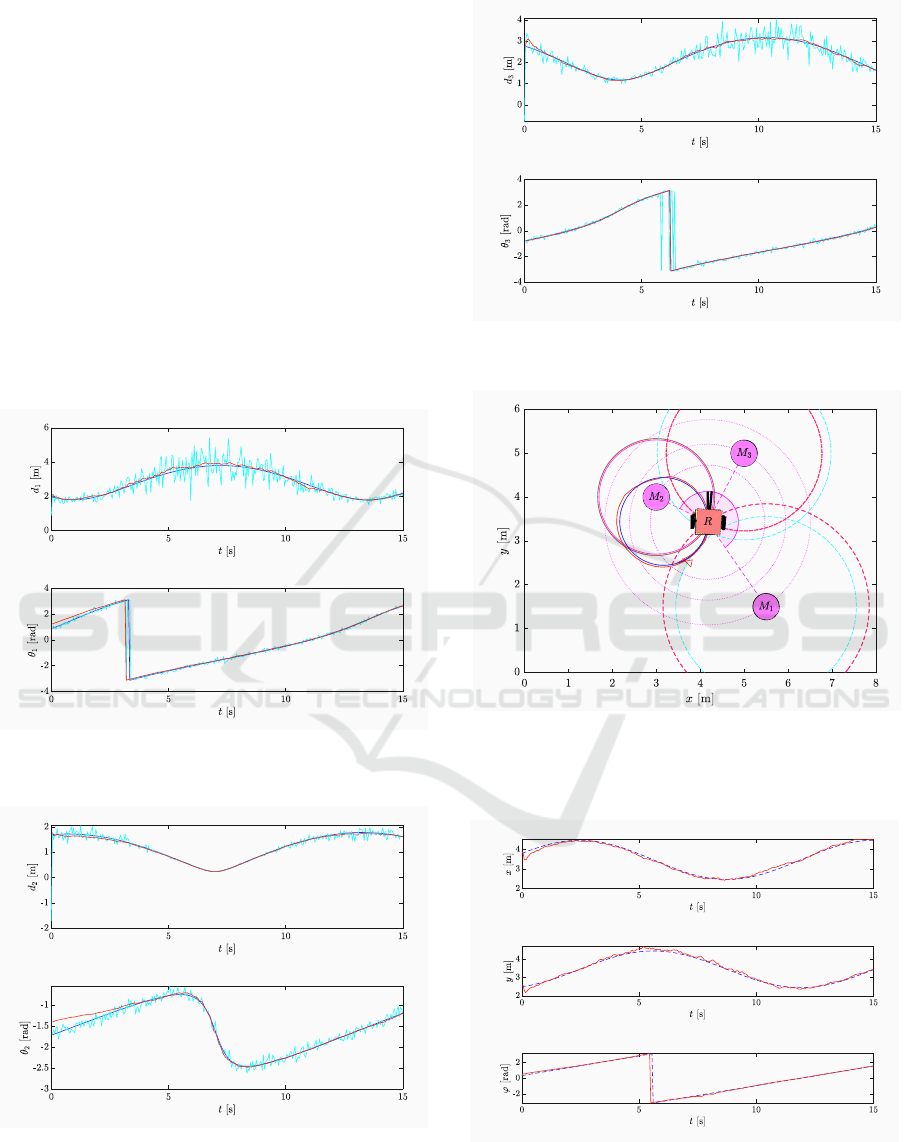
In the simulation we have used three landmarks

and the limited ﬁeld of view of the camera was not

taken into account . Figures 5 to 7 present the results

of all three partial estimators. It can be seen that the

distance measurement noise is largely dependant on

the distance to the landmark, but the output of each

partial estimator converges to the true value. Based

on the outputs of these estimators, the pose of the mo-

bile robot is calculated as an intersection of all three

solutions (circles) in the least squares sense (Figure

8). The pose estimate is shown in Figure 9.

Figure 5: Estimation of the landmark 1 state vector q

(blue

– true, red – estimate, cyan – measurement).

Figure 6: Estimation of the landmark 2 state vector q

(blue

– true, red – estimate, cyan – measurement).

Figure 7: Estimation of the landmark 3 state vector q

(blue

– true, red – estimate, cyan – measurement).

Figure 8: Estimation of the robot pose q at the end of

time (solid blue – true pose, solid red – estimated pose,

dashed cyan – measurements, dashed red – estimated mea-

surements).

Figure 9: Estimation of the robot state vector q (blue – true,

red – estimate).

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

550

4 CONCLUSION

Calibration of the system parameters is essential for

optimal performance of the localization algorithms.

We have showed a calibration procedure that can be

used to determine static transformation between the

camera and PTU coordinate frame. The procedure re-

quires only observation of the same set of points from

three different conﬁgurations of the PTU. This cali-

bration procedure is simple to deploy on a real set-

ting, without any special preparation of the environ-

ment solely for the calibration purposes.

In the development of the localization algorithm

system uncertainties were taken into account. Intro-

ducing the ﬂat ground surface constraint, the consid-

ered localization problem can be solved in the two

dimensional plane where the camera measures dis-

tances and angles to the visible landmarks. Assum-

ing normally distributed noise in image measurement

of landmark points, the standard deviation increases

predominantly in the direction of the image ray, pro-

portionally to the squared distance from the camera.

We have shown an approach that uses multiple

partial Kalman ﬁlters, where each ﬁlter estimates only

the distance and heading to the particular landmark,

and the outputs of these estimators are later used to

calculate the robot pose. Results demonstrate that

this is a feasible approach that converges to the true

pose of the mobile robot. The beneﬁt of this ap-

proach is computational efﬁciency, since the covari-

ance matrices are low dimensional. To reduce mem-

ory consumption during large-area localization, the

landmarks that have not been observed for a long time

can be made forgotten. The presented models are also

valid when the camera is moving. The proposed sys-

tem can be augmented with a control for tracking of

the nearest visible landmarks to reduce the time when

no landmarks are in the stereo camera ﬁeld of view.

ACKNOWLEDGEMENTS

The authors acknowledge the ﬁnancial support from

the Slovenian Research Agency (research core fund-

ing No. P2-0219).

REFERENCES

Agrawal, M. and Konolige, K. (2006). Real-time localiza-

tion in outdoor environments using stereo vision and

inexpensive GPS. In 18th Int. Conf. on Pattern Recog-

nition, volume 3, pages 1063–1068.

Betke, M. and Gurvits, L. (1997). Mobile robot localization

using landmarks. IEEE transactions on robotics and

automation, 13(2):251–263.

Bouguet, J.-Y. (2004). Camera calibration toolbox for Mat-

lab. [online] Available at: http://www.vision.caltech.

edu/bouguetj/calib doc [Accessed April 2019].

Chen, S. Y. (2012). Kalman ﬁlter for robot vision: a survey.

IEEE Trans. on Industrial Electronics, 59(11):4409–

4420.

Dellaert, F., Burgard, W., Fox, D., and Thrun, S. (1999).

Using the CONDENSATION algorithm for robust,

vision-based mobile robot localization. In IEEE Com-

puter Society Conf. on Computer Vision and Pattern

Recognition, volume 2, pages 588–594.

Du, X. and Tan, K. K. (2016). Comprehensive and

practical vision system for self-driving vehicle lane-

level localization. IEEE Trans. on Image Processing,

25(5):2075–2088.

Eggert, D. W., Lorusso, A., and Fisher, R. B. (1997). Esti-

mating 3-D rigid body transformations: a comparison

of four major algorithms. Machine vision and appli-

cations, 9(5–6):272–290.

Fischer, T., Pire, T.,

zek, P., Crist

oforis, P. D., and Faigl,

J. (2016). Stereo vision-based localization for hexa-

pod walking robots operating in rough terrains. In

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems, pages 2492–2497.

Fuentes-Pacheco, J., Ruiz-Ascencio, J., and Rend

on-

Mancha, J. M. (2015). Visual simultaneous localiza-

tion and mapping: a survey. Artiﬁcial Intelligence Re-

view, 43(1):55–81.

Garrido-Jurado, S., Munoz-Salinas, R., Madrid-Cuevas,

F. J., and Medina-Carnicer, R. (2016). Generation of

ﬁducial marker dictionaries using mixed integer linear

programming. Pattern Recognition, 51:481–491.

Hermann, R. and Krener, A. (1977). Nonlinear controlla-

bility and observability. IEEE Trans. on Automatic

Control, 22(5):728–740.

Kim, H., Liu, B., Goh, C. Y., Lee, S., and Myung, H. (2017).

Robust vehicle localization using entropy-weighted

particle ﬁlter-based data fusion of vertical and road in-

tensity information for a large scale urban area. IEEE

Robotics and Automation Letters, 2(3):1518–1524.

Konolige, K. and Agrawal, M. (2008). FrameSLAM: From

bundle adjustment to real-time visual mapping. IEEE

Trans. on Robotics, 24(5):1066–1077.

Mei, C., Sibley, G., Cummins, M., Newman, P., and Reid,

I. (2011). RSLAM: A system for large-scale mapping

in constant-time using stereo. International journal of

computer vision, 94(2):198–214.

Piasco, N., Marzat, J., and Sanfourche, M. (2016). Col-

laborative localization and formation ﬂying using dis-

tributed stereo-vision. In IEEE Int. Conf. on Robotics

and Automation, pages 1202–1207.

Se, S., Lowe, D., and Little, J. (2001). Vision-based mobile

robot localization and mapping using scale-invariant

features. In IEEE Int. Conf. on Robotics and Automa-

tion, volume 2, pages 2051–2058.

Tesli

c, L.,

Skrjanc, I., and Klan

car, G. (2011). EKF-based

localization of a wheeled mobile robot in structured

environments. Journal of Intelligent and Robotic Sys-

tems, 62:187–203.

Vision-based Localization of a Wheeled Mobile Robot with a Stereo Camera on a Pan-tilt Unit

551