Cryptanalysis of Homomorphic Encryption Schemes based on the
Aproximate GCD Problem
Tikaram Sanyashi
a
, Darshil Desai
b
and Bernard Menezes
c
Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Mumbai, India
Keywords:
Cloud Computing, Symmetric Key Encryption, Homomorphic Encryption, Approximate Greatest Common
Divisor Problem, Lattices, Orthogonal Lattice Attack.
Abstract:
Economies of scale make cloud computing an attractive option for small and medium enterprises. However,
loss of data integrity or data theft remain serious concerns. Homomorphic encryption which performs compu-
tations in the encrypted domain is a possible solution to address these concerns. Many partially homomorphic
encryption schemes that trade off functionality for lower storage and computation cost have been proposed.
However, not all these schemes have been adequately investigated from the security perspective. This paper
analyses a suite of such proposed schemes based on the hardness of the Approximate GCD problem. We show
that two of these schemes are vulnerable to the Orthogonal Lattice attack. The execution time of the attack
is a function of various parameters including message entropy. For the recommended set of parameters, the
execution time of the attack is no greater than 1 day on a regular laptop.
1 INTRODUCTION
Large scale cloud computing obviates the need for
significant investment in local computing resources.
However, storing sensitive information such as finan-
cial or medical data in the cloud environment may re-
sult in loss of data integity and/or data theft. One pos-
sible solution to maintaining data confidentiality is to
store user data in encrypted form. To perform opera-
tions on the data, it would need to be decrypted in the
cloud. This would expose the plaintext to the cloud
service provider and could compromise the privacy
of the data. Another possibility is to communicate the
encrypted data to the client who would decrypt it and
then perform the necessary computations on the data.
But that would defeat the goal of outsourcing com-
putation to the cloud. An attractive alternative is to
perform the operations on the cloud in the encrypted
domain. Cryptography offers a solution to this prob-
lem in the form of homomorphic encryption.
The notion of homomorphic encryption dates back
to 1978 when Rivest et al. (Rivest and Dertouzos,
1978) proposed it and called it “Privacy Homomor-
phism”. Through time, several encryption schemes
a
https://orcid.org/0000-0002-7434-0468
b
https://orcid.org/0000-0003-3283-3560
c
https://orcid.org/0000-0003-2997-9286
were introduced. These were partially homomorphic
- some were homomorphic with respect to addition
and some with respect to multiplication. Examples
include (Goldwasser and Micali, 1982), (ElGamal,
1985) (Benaloh, 1994) and (Paillier, 1999).
In 2009, the problem was finally addressed and
solved by Craig Gentry (Gentry et al., 2009) using
ideal lattices. Implementation of the solution required
very high storage and computation time. Even for a
single bit encryption, 2.3 Gigabytes and a bootstrap-
ping time of 30 minutes were required with lattice di-
mension over 32,000 making it impractical.
Many homomorphic schemes were proposed
based on the hardness of the Learning With Er-
ror (LWE) and Ring-Learning With Error (R-LWE)
problems. These include (Fan and Vercauteren,
2012; Brakerski, 2012; Bos et al., 2013; Brakerski
and Vaikuntanathan, 2014; Brakerski et al., 2014;
Costache and Smart, 2016). Also, some schemes
were constructed based on the hardness assumption
of integer GCD problem (Van Dijk et al., 2010; Coron
et al., 2011).
A drawback of many homomorphic encryption
schemes is the bit-by-bit encryption - each block of
ciphertext corresponds to a single bit of plaintext.
Moreover, computation tasks need to be converted to
binary addition and multiplication making the encryp-
tion scheme even more complicated. To reduce com-
Sanyashi, T., Desai, D. and Menezes, B.
Cryptanalysis of Homomorphic Encryption Schemes based on the Aproximate GCD Problem.
DOI: 10.5220/0008071605170522
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 517-522
ISBN: 978-989-758-378-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
517

plexity ciphertext packing techniques were studied.
For example, Peikert’s SIMD technique (Peikert et al.,
2008), Yasuda’s ideal lattice technique (Yasuda et al.,
2013), Cheon’s preprocessing of binary vector before
encryption technique (Cheon et al., 2013), Smart and
Vercuteren’s polynomial-CRT technique (Smart and
Vercauteren, 2014) etc. However, these schemes are
still not efficient enough to be acceptable in practice.
Somewhat Homomorphic Encryption (SHE)
schemes support a limited set of homomorphic
computations. One such SHE scheme was proposed
by Dyer et al. (Dyer et al., 2017). They presented
a suite of four symmetric key encryption schemes
- HE1 and HE2 are suitable for large entropy data
while their variants, HE1N and HE2N are appropriate
for small entropy data. The entropy represents the
number of bits present in the message. HE2N also
has the flexibility to be generalized to l-dimensions
with an increased level of security.
The encryption scheme is based on the hardness
of the Approximate Greatest Common Divisors prob-
lem (AGCD) (Howgrave-Graham, 2001). Given m
approximate multiples of p, c
i
= pq
i
+r
i
with small r
i
,
the approximate greatest common divisor p needs to
be recovered. The usual way to recover p is to guess
any two of r
1
, ··· , r
m
then compute greatest common
divisor of them as GCD(c
i
−r
i
,c
j
−r
j
). If the r
i
’s are
sufficiently small then the secret p can be recovered
easily using brute force search. However, if the per-
turbation r
i
is in the vicinity of p, then it is clearly
impossible to reconstruct p from the given informa-
tion.
The main contribution of this work is to demon-
strate that two of the four proposed schemes, HE1 and
HE1N are insecure. Even with a fairly small number
of ciphertexts, the plaintext and secret key can be de-
duced using the Orthogonal Lattice attack. The ex-
ecution time of the attack is a function of two main
parameters - the entropy of the message, ρ and the
maximum number of homomorphic operations, d that
can be performed on a given message before decryp-
tion fails. For small parameter settings, the execution
time is a few minutes and increases to a few hours for
larger parameter values.
Notations: In this paper, uppercase bold letters are
used to represent matrices, lowercase bold are for vec-
tors and regular lowercase are for constants.
x
$
←− Q denotes x is chosen uniformly at random
from space Q. lg denotes log base 2.
The paper is organized as follows. Section 2 con-
tains background material related to lattices. Section
3 summarizes the encryption schemes presented in
(Dyer et al., 2017) including the variants targeted in
our attack. In section 4, we present the cryptanalytic
attack on two of those schemes. We also include the
time to execute the attack. Section 5 concludes the
paper.
2 BACKGROUND
A lattice is a discrete (additive) subgroup of R
n
.
In particular, any subgroup of Z
n
is a special kind
of lattice referred to as an integer lattice. Let
b
1
, ··· , b
m
∈ Z
n
, n ≥ m be linearly independent. The
lattice, L , spanned by integer linear combinations of
b
1
, b
2
, ··· , b
m
is
L (b
1
, b
2
, ··· , b
m
) =

m
∑
i=0
x
i
b
i
: x
i
∈ Z

The set of vectors B = (b
1
, b
2
··· , b
m
) is called a basis
of lattice L, n, rank of lattice and m, dimension of
lattice. A full-rank lattice is one for which m = n.
The determinant of a lattice is n-dimensional vol-
ume of its fundamental parallelepiped, computed as
det(L)=
p
det(BB
T
), where B
T
is the transpose of B.
A lattice can have multiple bases spanning the same
lattice. The determinant of a lattice is independent of
the choice of basis.
Lattice reduction is often a key step in solving
problems based on lattices. It is used to find a basis
with short and nearly orthogonal vectors. The qual-
ity of the basis obtained from a reduction algorithm is
determined by the Hermite factor δ
n
0
where
||b
0
|| = δ
n
0
vol(L)
1
n
Here, b
0
represents the shortest non-zero vector after
lattice reduction. The smaller the Hermite factor, the
higher is the quality of the reduced basis.
The two main lattice reduction algorithms are
LLL and BKZ. BKZ2.0 is an optimized version of
BKZ. BKZ behaves differently based on block size k.
For k = 2 the algorithm runs in polynomial time and
outputs a basis equivalent to an LLL-reduced basis.
An increase in block size improves the quality of the
reduced basis but takes more time. In practice, the run
time of BKZ increases rapidly with block size and be-
comes practically infeasible for k > 30 or so. BKZ2.0
can handle a much larger block size and results in a
greatly reduced basis compared to BKZ.
Implementations of LLL, BKZ and BKZ 2.0 are
available in many software packages. In our imple-
mentations we have used SageMath and the fplll li-
braries.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
518

3 ENCRYPTION SCHEMES
TARGETED FOR ATTACK
The homomorphic encryption scheme presented in
(Dyer et al., 2017) is a 5-tuple (KeyGen, Enc, Dec,
Add, Mult). Based on its entropy, ρ, there are two
ways to encrypt a message, m, - HE1 and HE2. If ρ
is less than 32 bits, then HE1N or its more secure ver-
sion, HE2N, is used. A message with entropy greater
than 32 bits is encrypted with HE1 or its more secure
version HE2.
In the KeyGen step, two distinct large primes p
and q are employed. A security parameter, λ =
3dρ
2
,
(measured in bits) is selected and η is calculated as
η =
3dλ
2
−λ. The ranges of p and q are determined
by p ∈ [2
λ−1
, 2
λ
] and q ∈ [2
η−1
, 2
η
] . pq is publicly
known while p is the secret key. To prevent the fac-
torization of pq via Coppersmith’s method (Copper-
smith, 1997) or any other, a large value of λ is used.
The ciphertext, c of an integer, m, in HE1 is ob-
tained by computing
Enc(m, p) = m + rp (mod pq) (1)
where r
$
←− [1, q) is an ephemeral key.
Decryption involves a simple modulo p operation
Dec(c, p) = c (mod p)
It is clear from 1 that a message with small en-
tropy, ρ, is vulnerable to a brute force attack. There-
fore to encrypt such a message, a modified scheme,
HE1N, is used - this adds an extra noise term during
encryption to increase entropy and thereby thwart a
possible brute force attack. The secret key for the en-
cryption scheme is now the pair, (k, p). Here, k is an
integer and its size is a security parameter. Key gen-
eration for HE1N is as in HE1 but with the following
modification
λ =
3dρ
0
2
η =
3dλ
2
−λ where ρ
0
= ρ + lg k .
Encryption of an integer, m using HE1N is com-
puted using
c = Enc(m, p, k) = m + [p, k]

r
s

(mod pq)
where r
$
←− [1, q) and s
$
←− [0, k).
Message m is obtained from the ciphertext c by
performing the following two modulo computations
in sequence
Dec(c, sk) = (c mod p) mod k
HE2 and HE2N are the more secure counterparts
of HE1 and HE1N respectively. Encryption of mes-
sages with HE2 and HE2N is similar to that with HE1
and HE1N but the new ciphertext is a vector of two
components with added randomness to make it more
secure.
The key generation process of HE2 and HE2N is
also similar to that of HE1 and HE1N. It involves
sampling of two prime numbers, a
i
$
←− [1, pq), i ∈
{1, 2} with a
1
, a
2
, (a
1
− a
2
) 6= 0 (mod p and mod
q). It computes a re-encryption matrix R (for homo-
morphic multiplication) as

1 −2α
1
α
1
α
1
−α
2
α
2
+ 1 α
2

where,
α
1
= β
−1
(σa
1
+ ρp −a
2
1
),
α
2
= β
−1
(σa
2
+ ρp −a
2
2
),
with β = 2(a
2
−a
1
)
2
, ρ
$
←− [0, q] and σ
$
←− [0, pq)
The ciphertext of an integer m in HE2 is a vector
of two components calculated as
c = Enc(m, sk) = m

1
1

+

p a
1
p a
2

r
s

(mod pq)
Here r
$
←− [1, q) and s
$
←− [1, pq) are independent
ephemeral secrets for each encryption resulting in dif-
ferent ciphertexts for the same message m.
Decryption of ciphertext c = (c
1
, c
2
) involves
computation of
Dec(c, sk) = γ
T
∗c (mod p),
where γ
T
= (a
2
−a
1
)
−1
[a
2
, − a
1
].
The ciphertext with HE2N is a vector of two com-
ponents computed as
c = Enc(m, sk) = m

1
1

+

p k a
1
p k a
2

"
r
s
t
#
(mod pq)
Here r
$
←− [1, q), s
$
←− [1, k) and t
$
←− [1, pq).
Decryption of ciphertext c = (c
1
, c
2
) involves
computation of
Dec(c, sk) = γ
T
c (mod p) mod k
where γ is defined as in the case of HE2. The encryp-
tion scheme can be generalized to l−dimensions as





c
1
c
2
.
.
.
c
l





=





m
m
.
.
.
m





+





p a
11
··· a
1(l−1)
p a
21
··· a
2(l−1)
.
.
.
.
.
. ···
.
.
.
p a
l1
··· a
l(l−1)










r
s
1
.
.
.
s
(l−1)





(mod pq)
c = m + As (mod pq)
The above equality resembles LWE but there are
some major differences. In LWE, the cipher c and
matrix A are known but here A itself is a secret and s
is an ephemeral key which makes it even harder.
Cryptanalysis of Homomorphic Encryption Schemes based on the Aproximate GCD Problem
519

The hardness increases as dimension l increases
but increasing l progressively makes the encryption
scheme impractical. Therefore there is a tradeoff be-
tween hardness and practicality. When l = 1 the prob-
lem converges to AGCD problem which can be solved
for the parameter setting provided in (Dyer et al.,
2017). In the next section, we show how HE1 and
its low entropy version HE1N may be compromised.
4 CRYPTANALYSIS
In this section, we focus on attacking HE1 and HE1N
using the Orthogonal Lattice Attack.
4.1 Attacking HE1 and HE1N
We explored two lattice-based techniques to recover
the secret key of the encryption scheme viz. Orthogo-
nal Lattice attack (OLA) and Simultaneous Diophan-
tine Approximation Attack (SDA). In each case, we
recovered the plaintext and this further leads to re-
covery of the secret key p.
Both of these attacks perform well in practice
though OLA runs comparatively faster compared to
SDA. In the interest of brevity, we focus on the OLA
Attack here.
The notion of the Orthogonal Lattice was first in-
troduced by Nguyen and Stern (Nguyen and Stern,
2001) to crack the Qu-Vanstone cryptosystem. Since
then it has been used for cryptanalysis of various
other cryptosytems. Appendix B.1 of (Van Dijk
et al., 2010) also mentioned a way to recover vec-
tors orthogonal to cipher text (c
1
, ··· , c
z
), where
(c
1
, ··· , c
z
) represents ciphertext corresponding to
message (m
1
, ··· , m
z
). The idea is that a lattice or-
thogonal to (c
1
, ··· , c
z
) contains a sublattice orthog-
onal to both (m
1
, ··· , m
z
) and (q
1
, ··· , q
z
). We used
techniques of (Van Dijk et al., 2010) to break the en-
cryption schemes, HE1 and HE1N.
4.2 Attack Details
Construct a lattice, L spanned by the rows of follow-
ing z ×(z + 1) basis matrix T.
T =




c
1
M
1
c
2
M
2
.
.
.
.
.
.
c
z
M
z




c
i
is the ciphertext corresponding to message m
i
and
M
i
is an upper bound on the value of m
i
. Any vector
u = (u
0
, u
1
, ··· , u
z
) in the lattice T can be represented
by
u = (α
1
, ··· , α
z
)T
= (
z
∑
i=1
α
i
c
i
, α
1
M
1
, ··· , α
z
M
z
)
for some integer values α
i
. The main observation is
that
u
0
−
z
∑
i=1
u
i
M
i
.m
i
=
z
∑
i=1
α
i
.c
i
−
z
∑
i=1
α
i
M
i
M
i
.m
i
(mod p)
=
z
∑
i=1
α
i
(c
i
−m
i
) (mod p)
= 0
As the value of p is not known beforehand, we
want a vector that satisfies
u
0
−
z
∑
i=1
u
i
M
i
.m
i
≤ |u
0
|+ |
z
∑
i=1
u
i
M
i
.m
i
|
≤
z
∑
i=0
|u
i
| ≤
p
2
The determinant of the Gram matrix TT
T
is
bounded by product of the norms of the columns of
matrix T, which is M
z
.
q
c
2
1
+ c
2
2
+ ···+ c
2
z
. Accord-
ing to Gaussian heuristic the shortest vector is as short
as
√
zM.
z
q
c
2
1
+ c
2
2
+ ···+ c
2
z
. To obtain the shortest
vector u, we need this to be as short as p. The condi-
tion to obtain such a vector can be formulated as
M.
z
√
c < p
where c = c
2
1
+ c
2
2
+ ···+ c
2
z
,
The above gives a lower bound on the number
of ciphertexts, z, needed for plaintext recovery as
z >
γ
λ−ρ
. Here, γ, λ, ρ represent the number of bits
in ciphertext c secret key p and message m respec-
tively. When z >
γ
λ−ρ
, then lattice reduction is able
to recover the short vectors in T subject to constraints
on computation time.
Lattice reduction is performed on the basis matrix,
T. The first row of T is (1, −
m
1
M
1
, ··· , −
m
z
M
z
). From this
we recovered the plaintexts, m
i
. The secret key, p, is
obtained by computing GCD(c
i
−m
i
, c
j
−m
j
).
4.3 Results
We implemented the attack of the previous section
and ran it for several parameter sets including those
mentioned in (Dyer et al., 2017). All experiments
were performed on Intel i5 Gen 4, with 3.5 GHz clock
and 8 GB DRAM running Ubuntu 16.04 64-bit LTS.
We were successful in recovering the message and
later the secret key itself for all parameter values in
SECRYPT 2019 - 16th International Conference on Security and Cryptography
520

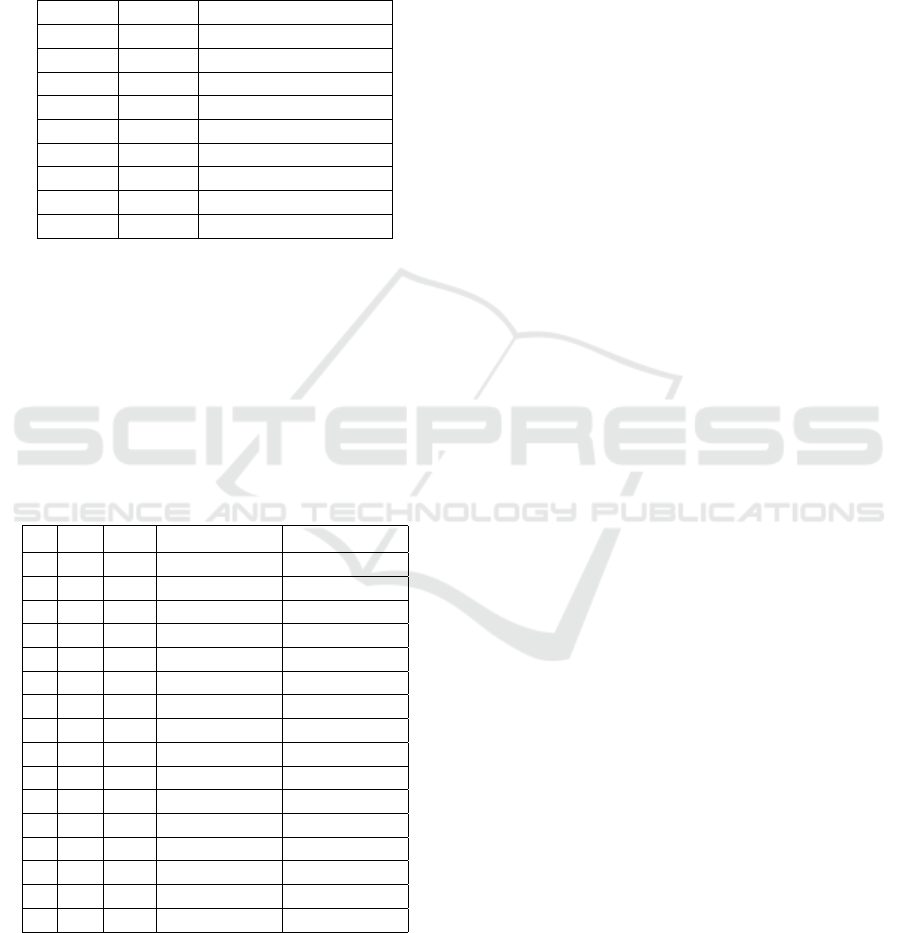
Table 1. The total time is dominated by the time for
lattice reduction and increases greatly with message
size and d. For the highest parameter setting in (Dyer
et al., 2017), we could recover the message and the
key in about 18 hours.
Table 1: Attack time for recovering plaintext in HE1 en-
cryption scheme.
d ρ Attack time(Min)
2 32 .25
2 64 3.5
2 128 75
3 32 .25
3 64 4
3 128 430
4 32 .5
4 64 20
4 128 1070
For attacking HE1N, we followed the same tech-
nique as for HE1. We first used the Orthogonal Lat-
tice attack to recover m + ks from c = m + ks + pr
(Attack 1) and later the same technique to recover m
from m + ks (Attack 2).
For the highest parameter setting mentioned in
(Dyer et al., 2017) we could recover the message and
hence the secret key p in about 20 hours as shown in
Table 2.
Table 2: Attack time for recovering plaintext in HE1N en-
cryption scheme.
d ρ ρ
0
Attack1(Min) Attack2(Sec)
2 1 32 .25 .0106
2 1 64 13 .0103
2 1 128 460 .0359
2 8 32 .30 .0122
2 8 64 16 .0134
2 8 128 470 .0133
2 16 64 20 .0122
2 16 128 490 .0125
3 1 32 .28 .0126
3 1 64 22 .0105
3 1 128 510 .0125
3 8 32 .32 .0125
3 8 64 22 .0142
3 8 128 520 .0144
3 16 64 30 .0502
3 16 128 1195 .0508
5 CONCLUSION
In this paper, we studied the security of the encryp-
tion schemes presented in (Dyer et al., 2017). These
schemes are based on the hardness of the AGCD prob-
lem. We investigated the possible application of the
Orthogonal Lattice attack to crack these schemes. Our
experiments indicate that the parameter values rec-
ommended for the HE1 and HE1N schemes are too
small to resist attack. The plaintext and key for these
schemes may be recovered within a day on a regular
laptop even for the highest parameter settings.
Encryption schemes HE2 and HE2N are also
based on the hardness of the AGCD problem. How-
ever, as of now, we are unable to find any attack tech-
niques to crack these and its subsequent versions.
REFERENCES
Benaloh, J. (1994). Dense probabilistic encryption. In Pro-
ceedings of the workshop on selected areas of cryp-
tography, pages 120–128.
Bos, J. W., Lauter, K., Loftus, J., and Naehrig, M. (2013).
Improved security for a ring-based fully homomor-
phic encryption scheme. In IMA International Con-
ference on Cryptography and Coding, pages 45–64.
Springer.
Brakerski, Z. (2012). Fully homomorphic encryption
without modulus switching from classical gapsvp.
In Annual Cryptology Conference, pages 868–886.
Springer.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014).
(leveled) fully homomorphic encryption without boot-
strapping. ACM Transactions on Computation Theory
(TOCT), 6(3):13.
Brakerski, Z. and Vaikuntanathan, V. (2014). Efficient fully
homomorphic encryption from (standard) lwe. SIAM
Journal on Computing, 43(2):831–871.
Cheon, J. H., Coron, J.-S., Kim, J., Lee, M. S., Lepoint,
T., Tibouchi, M., and Yun, A. (2013). Batch fully ho-
momorphic encryption over the integers. In Annual
International Conference on the Theory and Appli-
cations of Cryptographic Techniques, pages 315–335.
Springer.
Coppersmith, D. (1997). Small solutions to polynomial
equations, and low exponent rsa vulnerabilities. Jour-
nal of Cryptology, 10(4):233–260.
Coron, J.-S., Mandal, A., Naccache, D., and Tibouchi, M.
(2011). Fully homomorphic encryption over the inte-
gers with shorter public keys. In Annual Cryptology
Conference, pages 487–504. Springer.
Costache, A. and Smart, N. P. (2016). Which ring based
somewhat homomorphic encryption scheme is best?
In Cryptographers’ Track at the RSA Conference,
pages 325–340. Springer.
Cryptanalysis of Homomorphic Encryption Schemes based on the Aproximate GCD Problem
521

Dyer, J., Dyer, M., and Xu, J. (2017). Practical homomor-
phic encryption over the integers for secure computa-
tion in the cloud. In IMA International Conference on
Cryptography and Coding, pages 44–76. Springer.
ElGamal, T. (1985). A public key cryptosystem and a signa-
ture scheme based on discrete logarithms. IEEE trans-
actions on information theory, 31(4):469–472.
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. IACR Cryptology ePrint
Archive, 2012:144.
Gentry, C. et al. (2009). Fully homomorphic encryption
using ideal lattices. In Stoc, volume 9, pages 169–178.
Goldwasser, S. and Micali, S. (1982). Probabilistic en-
cryption & how to play mental poker keeping secret
all partial information. In Proceedings of the four-
teenth annual ACM symposium on Theory of comput-
ing, pages 365–377. Academic Press, New York.
Howgrave-Graham, N. (2001). Approximate integer com-
mon divisors. In International Cryptography and Lat-
tices Conference, pages 51–66. Springer.
Nguyen, P. Q. and Stern, J. (2001). The two faces of lattices
in cryptology. In International Cryptography and Lat-
tices Conference, pages 146–180. Springer.
Paillier, P. (1999). Public-key cryptosystems based on com-
posite degree residuosity classes. In International
Conference on the Theory and Applications of Cryp-
tographic Techniques, pages 223–238. Springer.
Peikert, C., Vaikuntanathan, V., and Waters, B. (2008).
A framework for efficient and composable oblivious
transfer. In Annual international cryptology confer-
ence, pages 554–571. Springer.
Rivest, R., A. L. and Dertouzos, M. (1978). Paper. In On
Data Banks and Privacy Homomorphisms. Founda-
tions of Secure Computation, ed. by RA DeMillo, et.
al. Academic Press, New York.
Smart, N. P. and Vercauteren, F. (2014). Fully homomor-
phic simd operations. Designs, codes and cryptogra-
phy, 71(1):57–81.
Van Dijk, M., Gentry, C., Halevi, S., and Vaikuntanathan, V.
(2010). Fully homomorphic encryption over the inte-
gers. In Annual International Conference on the The-
ory and Applications of Cryptographic Techniques,
pages 24–43. Springer.
Yasuda, M., Shimoyama, T., Kogure, J., Yokoyama, K., and
Koshiba, T. (2013). Packed homomorphic encryption
based on ideal lattices and its application to biomet-
rics. In International Conference on Availability, Re-
liability, and Security, pages 55–74. Springer.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
522