A Fast Level Set Based on New Signed Pressure Force Function
for Nuclei Images Segmentation
Ru Xu
1,*
, Wei Zhang
2
, Guangfang Yang
3
1,*
College of Big Data and Intelligent Engineering, Yangtze Normal University, Chongqing 408100, China
2
College of Computer Science, Chongqing University, Chongqing 400030, China
3
College of Mathematics and Statistics, Chongqing University, Chongqing 400044, China
Keywords: Image Processing, Level set method, Signed pressure force, Legendre polynomials, Edge stopping function.
Abstract: In the paper, a fast level set for nuclei images is proposed. It is performed with a novel method, mainly
combining idea of signed pressure force function with Legendre polynomials. The advantages of the
proposed method are as follows. On the one hand, a controlled signed pressure force function based on 1-D
Legendre polynomials (LPSPF
+
) can stop the final contours at blurred and multiple objects edges, especially
for nuclei images segmentation. On the other hand, we set multiple ball contour as initial contour to
automatically detect the exterior and interior boundaries in the image. Ultimately, an improved edge
stopping function is applied to fast and robustly capture the edge of multiple regions of interest (ROI).
Experimental results demonstrate that our method is higher and faster accuracy than other models on nuclei
images and other images with large size, or low-contrast.
1 INTRODUCTION
Image segmentation is an essential problem, which
is applied to divide the given image into several
sections, including ROI and background, especially
for the clinical diagnosis from medical images. To
execute nuclei images segmentation well, a variety
of research has been done and many excellent
methods have been presented, like watershed-based
segmentation and active contour models (ACM).
However, the former has limitation that is prone to
over-segmentation. To catch final ROI, the basic
thought of ACM is to evolve a curve for the detected
target according to energy-minimizing theory.
The established ACM can be widely classified
into two categories: region-based models and edge-
based models. Besides, some models which combine
edge-based models with region-based models have
been presented in recent years. And edge-based
models mainly rely on the gradient image to stop the
evolution of variation curve. Nevertheless, region-
based models almost employ statistical characteristic
inside and outside the active contour to restrict the
evolution of curves.
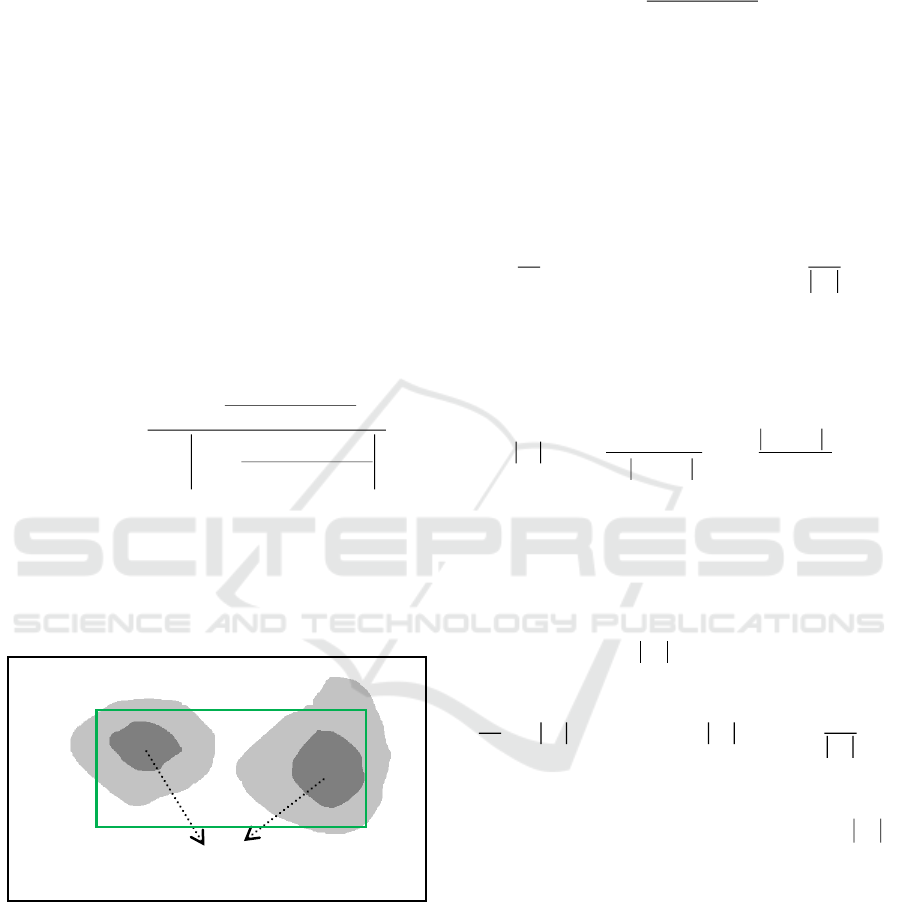
Figure 1: Segmentation results of our method on polynuc
-lear images. (Blue curves are the final evolving curves.)
In recent years, many high efficient and accuracy
solutions have been proposed to amend the weak-
ness of Chan-Vese model (Chan, T. F., 2001). Li et
al. (Li Chunming, 2008) proposed the LBF model
that can accurately extract the local images, but its
calculations take a long time. Li et al. (Li Chunming,
2010) presented the idea of the Bias field, and it can
deal with intensity inhomogeneity problem by
calculating and correcting the bias field. Zhang et al.
(Zhang Kaihua, 2010) proposed a region-based
10
Xu, R., Zhang, W. and Yang, G.
A Fast Level Set Based on New Signed Pressure Force Function for Nuclei Images Segmentation.
DOI: 10.5220/0008096000100017
In Proceedings of the International Conference on Advances in Computer Technology, Information Science and Communications (CTISC 2019), pages 10-17
ISBN: 978-989-758-357-5
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ACM which is performed with a novel level set
method, described as SBGFRLS method. And it can
reduce the costly re-initialization of the previous
level set method to make it more efficient. Based on
the idea of SBGFRLS method, various approaches
about improved signed pressure force function were
proposed successively. An edge independent
segmentation approach Legendre Level Set (L2S)
which is robust to variations in intensity levels was
proposed (Suvadip Mukherjee, 2014). Zhang et al.
proposed an improved ACM which is driven by the
region-scalable and local Gaussian-distribution
fitting energy for image segmentation, named the
RSLGD model (Zhang Wei, 2017). He et al.
proposed a promotional local or global ACM that is
driven by Legendre polynomials to optimize
SBGFRLS method (He Guanghui, 2018). And Hai et
al. (Min H, 2018) proposed a unique level set
method that is a nonlinear approximation method to
solve the nonconvex optimization problem, named
Local Approximation of Taylor Expansion (LATE) .
The purpose of the paper is to segment nuclei
images (Wu Z, 2012, Park C, 2013) in Figure 1,
which have several characteristics including multiple
objects, large size, low-contrast and some small
regions of interest. To tackle these problems, a
controllable level set method driven by pressure
force function based on 1-D Legendre polynomial is
proposed. Meanwhile, we introduce an edge
stopping function (ESF) to fast get edge information
of nuclei images. Experiments show that our model
can enhance efficiency, accuracy and generalization
performance of final segmentation results.
The remainder of this paper is planned as follows.
Section 2 briefly reviews of the SBGFRLS and L2S
method. Section 3 demonstrates the proposed model.
In addition, we perform various experiments, make a
comparison and explore the quantitative analysis
with other models in the Section 4. Eventually, in
Section 5, we give a summary for the above work.
2 THE RELATED WORK
2.1 The SBGFRLS Method
On the base of GAC model and CV model, K.
Zhang et al. presented selective binary and Gaussian
filtering regularized level set (SBGFRLS), which
developed a region based on the singed pressure
force function (SPF) to effectively stop the contour
at weak or blurred edges. This SPF function can
control the evolutionary direction. Besides, the
opposite symbols around the edges of ROI in the
function can make the contour to shrink when it is
outside the boundary and to expand when it is inside
the boundary. And the SPF function is defined as
follows:













2
)(
2
)(
))((
21
21
cc
xIxma
cc
xI
xIspf
(1)
Where the range of
))(( xIspf
values is
]1,1[
, and
21
,cc
are to mainly approximate two dynamic image
average intensity in the regions inside and outside
the active contour
C
(i.e. the zero level set function

). Then
21
,cc
are expressed as equation (2).





dxH
dxHxI
c
)(
)()(
1


,





dxH
dxHxI
c
))(-1(
))(-1)((
2


(2)
Thus, the gradient descent flow equation of
SBGFRLS model can be donated as follows:









))(())(())(( xIspfdivxIspf
t
(3)
Where

is a adjustable parameter that can be
changed with regard to different images. Moreover,
the regular term

 )/(div
can be abandoned,
because we can use Gaussian filter to smooth the
level set function to keep the evolutionary contours
regular. Besides, the term

 ))(( xIspf
can be
removed because the method utilizes the statistical
in formation of the regions. Thus the final gradient
descent flow equation is given as in equation (4).





))(( xIspf
t
(4)
Experiments show it can distinctly reduce costly
computing of previous methods. But the method has
a drawback which can’t segment images with intensi
-ty inhomogeneity.
2.2 The L2S Method
In 2014, Suvadip et al. presented a novel region-
based segmentation method by employing Legendre
polynomials to approximate image region intensity,
and it can effectively solve the image with intensity
inhomogeneity problem. The significant contribution
of the L2S method is to formalized and generalize
the classical CV model, which can replaced the two
scalars
21
,cc
with two continuous derivable functions
A Fast Level Set Based on New Signed Pressure Force Function for Nuclei Images Segmentation
11

)(),(
21
xcxc
nn
defined in equation (5). And the two fun
-ctions are assumed to be a linear combination of a
few Legendre basis functions, respectively.
)()(
1
xLxc
k
k
k
n



,
)()(
2
xLxc
k
k
k
n



(5)
Where
k
L
is a multidimensional Legendre
polynomi -al. Its meaning is the outer product of the
1-D counterparts which can be written easily.
However, we can get the 2-D Legendre polynomial
by computing
)()(),( ylxlyxL
kkk

,
2
]1,1[),( yx
.
Then
k
l
is a simple 1-D Legendre polynomial which
can be written as:
iik
k
i
k
k
xx
i
k
xl )1()1(
2
1
)(
0













(6)
Therefore, we can write the energy functional of
the L2S model as the following formula:
dx
x
x
x
BdxxHBxLxI
AdxxHAxLxIE
T
TSL











)(
)(
))((
)))((1()()(
))(()()()(
2
2
2
2
2
2
1
2
2





(7)
Where
0,0,0
21
 
are three adjustable para
-meters. And the regularized Heaviside function
)(  H
can be defined as equation (8). The derivative
of
)(

H
is on behalf of the dispersed Dirac function
expressed as follows.
))arctan(
2
1(
2
1
)(


x
xH 
(8)
)(
)(
22
x
x






(9)
In order to compute optimal
A
and
B
, we can
perform
0/  AE
and
0/  BE
, then the symbolic
solution
A
ˆ
and
B
ˆ
can be caught by computing the
equation (10) and (11).
 



 dxxHxIxLMPA ))(()()(
ˆ
1
1

(10)
 
dxHxIxLMQB



 ))(1)(()(
ˆ
1
2

(11)
Where
PM,
and
Q
are defined in (Suvadip Mukherjee,
2014), and discretization of expression are written as:
 

ji
ji
ddxHP ,))((
,

(12)
 

ji
ji
ddxHQ ,)))((1(
,

(13)
Where
 ,
indicates the Euclidean inner product
operator and
Nji  ,0
. Then, the following
gradient descent flow equation can be deduced.
)()(
ˆ
)()(
ˆ
)()()(
22





















div
BxLxIAxLxI
t
TT
(14)
Note that the initial boundary value conditions
are expressed as the following equation.
0
0
 
t
,
0
ˆ
)(



 n




(15)
Ultimately, it commendably segments images
with intensity inhomogeneity. However, the CPU
time of results take a long time because of Legendre
basis functions. And it can’t deal with images
including multiple objects, like nuclei images.
3 THE PROPOSED METHOD
Like existing level set methods, we still hypothetical
-ly reflect on a image, like nuclei images. For each
pixel
x
in the given image, let
 
0)(:
0
 xx

is the
zero level set function that partitions image
I
into
two parts
}0)(:{
1
 xx

and
}0)(:{
2
 xx

. In
fact, we can minimize the entire energy functional of
I
to get the ideal segmentation results.
First of all, the gradient descent flow equation of
L2S model can be reworded as equation (16) by
deducing the equation (14) .
)()(
)
2
)
ˆ
ˆ
)((
)(()
ˆ
ˆ
)((2)(




















div
BAxL
xIBAxL
t
TT
TT
(16)
Where
),,,(
21 N
aaaA 
and
),,,(
21 N
bbbB 
are
the coefficient vectors for two regions
1

and
2

,
while
2
)1(  mN
is the number of basis functions
and
m
is the degree of Legendre polynomial (i.e. m-
D Legend -re polynomial). Note that 0-D Legendre
polynomial reduces to the famous CV model, thus
CTISC 2019 - International Conference on Advances in Computer Technology, Information Science and Communications
12

the proposed model presents a generalized
framework.
In practice, we often use 1-D Legendre polyno
-mials, i.e.
1m
. Particularly, we assume that the
purpose is to segment an image
I
with
300300
size.
By computing and analyzing the parameters, the size
of
)(,
ˆ
,
ˆ
xLBA
TT
,
)
ˆ
ˆ
)((
TT
BAxL 
and
)
ˆ
ˆ
)((
TT
BAxL 
are
14
,
14
,
4300
2

,
1300
2

and
1300
2

. However, in
our experiments, the term
)
ˆ
ˆ
)((
TT
BAxL 
is resized as
)
ˆ
ˆ
)((
TT
BAxL 
with
300300
size, according to the
original image size.
Inspired by (Zhang kaihua, 2010, Suvadip
Mukherjee, 2014, and He Guanghui, 2018), on the
one hand, we combine advantage of L2S model with
SBGFRLS model to develop a new SPF function
based on Legendre polynomial with signed pressure
force function (LPSPF
＋
), which can be donated as
follows.




















1
)
ˆ
ˆ
)((
)(
1
)
ˆ
ˆ
)((
)(
))((
TT
TT
BAxL
xIxma
BAxL
xI
xIlpspf
(17)
Where
))(( xIlpspf

combines
))(( xIspf
with 1-D
Legendre polynomial to overcome the problems of
SBGFRLS model that is not good for images with
intensity inhomogeneity. Different from SBGFRLS
model, we add a parameter

to effectively restrain
convergence scale inside or outside of ROI.
Figure 2: The labels of the SPF function inside and outside
the object are opposite.
The significance of
))(( xIlpspf

can be explained
as follows. With regard to Figure 2, we assume that
the intensities inside and outside the
C
are homogene
-ous. It is intuitive that
)(,)(
21
IMaxccIMin 
in the
SBGFRLS model. Since we substitute scalars
21
,cc
by two continuous derivable functions
)(),(
21
xcxc
nn
, it
is similar that
))(()(),())((
21
xIMaxxcxcxIMin
nn

, and
equal labels cannot be caught synchronous wherever
the contour is. So,we can deduce equation (18).
))((
2
)
ˆ
ˆ
)((
))(( xIMax
BAxL
xIMin
TT



(18)
Obviously, the signs of the SPF function in
equation (1) are identical to what Figure 2 shows, so
equation (17) can serve as an SPF function.
Meanwhile, we utilize a constant

to replace
)
ˆ
ˆ
)((2
TT
BAxL 
for simplicity. Substituting the SPF
function in equation (16) for the ESF in equation (5),
the level set formulation of the proposed model is as
follows:
)()())(()(










divxIlpspf
t
(19)
On the other hand, to capture the edges of ROI
and speed up the segmentation for images with
multiple objects, we employ the edge indicator
function
)( Ig 
expressed as equation (20):
2
2
2
1
( ) ,
1
GI
g I min exp
GI








  


  



(20)
Where

and
IG *

are the gradient operator and
the convolution of image
I
with Gaussian function

G
. The purpose is to converge smaller values at
edges.
Finally, to speed up the convergence, we
substitute
)( 
with
 
. Thus, the gradient flow
equation of our model can be donated as:
))(())((











IgdivxIlpspf
t
(21)
Where
0,0 

are two adjustable parameters.
And the curvature of level-curve

is
( / )div


.

is the parameter of the second term in equation
(20). And it’s significant that initial boundary value
conditions are equation (15). The nature of equation
(21) is to solve a partial differential equation with a
finite difference method.
Max(I) +
Min(I) -
2
c
1
c
A Fast Level Set Based on New Signed Pressure Force Function for Nuclei Images Segmentation
13

4 EXPERIMENTAL RESULTS
4.1 Data Set and Algorithm of The Pro
-posed Model
To demonstrate the efficacy of the proposed method,
we have performed experiments on 664 images in
2018 Data Science Bowl. The nuclei data set of
stage1_train chiefly can be categorized into 4
classes：107 colorized and multicellular images, 89
low contrast and multicellular images, 16 polynucle
-ar images and 452 gray multicellular images. Note
that it contains the segmented masked image of all
nucleus for each image (i.e. ground truth).
In the paper, we have proposed a fast level set
based on combining Legendre Polynomial with
signed pressure force function (LPSPF
+
). Its main
implementation can be described at Algorithm 1.
Algorithm 1: The implementation of the proposed method
Input: a nuclei image
)(xI
Initialization:

,,,,,,,,
0
MaxIter
Output: level set function
)(x

1. for i = 1:
MaxIter
2. compute
BA
ˆ
,
ˆ
,
))(( xIlpspf

and
))(( xIg 
3. update
1i

by solving equation (21)
4. optimize

with

 G*
to enhance the
efficiency
5. if
MaxIteriter 
or


)(/)()(
1 iii
lenlenlen

6. stop the iteration
7. else
8. repeat step 2 - 4
9. end
10. end
Where
)(len
is to catch the length of
))((

H
in
Algorithm 1. In the paper, we choose the Gaussian
filter to optimize level set function

. To accelerate
the evolution, we utilize multiple ball contour to
replace
0

. Its advantage is to catch gray value and
gradient about the target objects as much as possible,
so that multiple objects in a image can be segmented
fast and automatically. Besides, the parameter

can
restrain the gray value of the object to be segmented.
And

is proportion to gray value, and the range of

is
0

.
4.2 Results of the Proposed Method
In this section, a variety of nuclei images are used to
valid the robustness and performance of our model
and its experimental results are shown in Figure 1,
Figure 3 and Figure 6. Some recent methods referred
in L2S, RSLGD, SBGFRLS, and LGLP are tested
on synthetic and real images and above data set to
demonstrate advantages of the proposed model. And
the whole works are performed in Matlab R2014a on
a personal computer with Inter Xeon CPU E3-
1226 3.30 GHz and 8GB RAM. By default, those
parameters are set as
80,


,1

1,


,4

,001.0
2,


,100MaxIter
.1

The initial con
-tour is set as multiple balls which are equally
distributed with
25r
in the whole image.
Figure 3: Segmentation results of our proposed method on
low-contrast and multicellular images. Col 1: input images.
Col 2:segmentation results. Col 3: ground truth. (Blue
curves are the final evolving curves.)
On the one hand, according to the segmentation
results in Figure 1, Figure 3 and Figure 5, we can
observe that the proposed model can accurately get
multiple objects boundaries, especially with regard
to multicellular or polynuclear images. Adding and
adjusting the constraint parameter

can effectively
catch polynuclear contour in Figure 1. And the range
of

is
]4,5.2[
in our experiment for images in
Figure 1.
The low contrast and multicellular images of
2018 Data Science Bowl can be segmented shown in
Figure 3. The first column is input image, and we
can find the difference which the second image in
the first row is different from the first image. The
reason is that using 1-D Legendre polynomials can
effectually increase the contrast of image, like
histogram equalization. Then, we get multicellular
boundaries with ESF in equation (20).
CTISC 2019 - International Conference on Advances in Computer Technology, Information Science and Communications
14

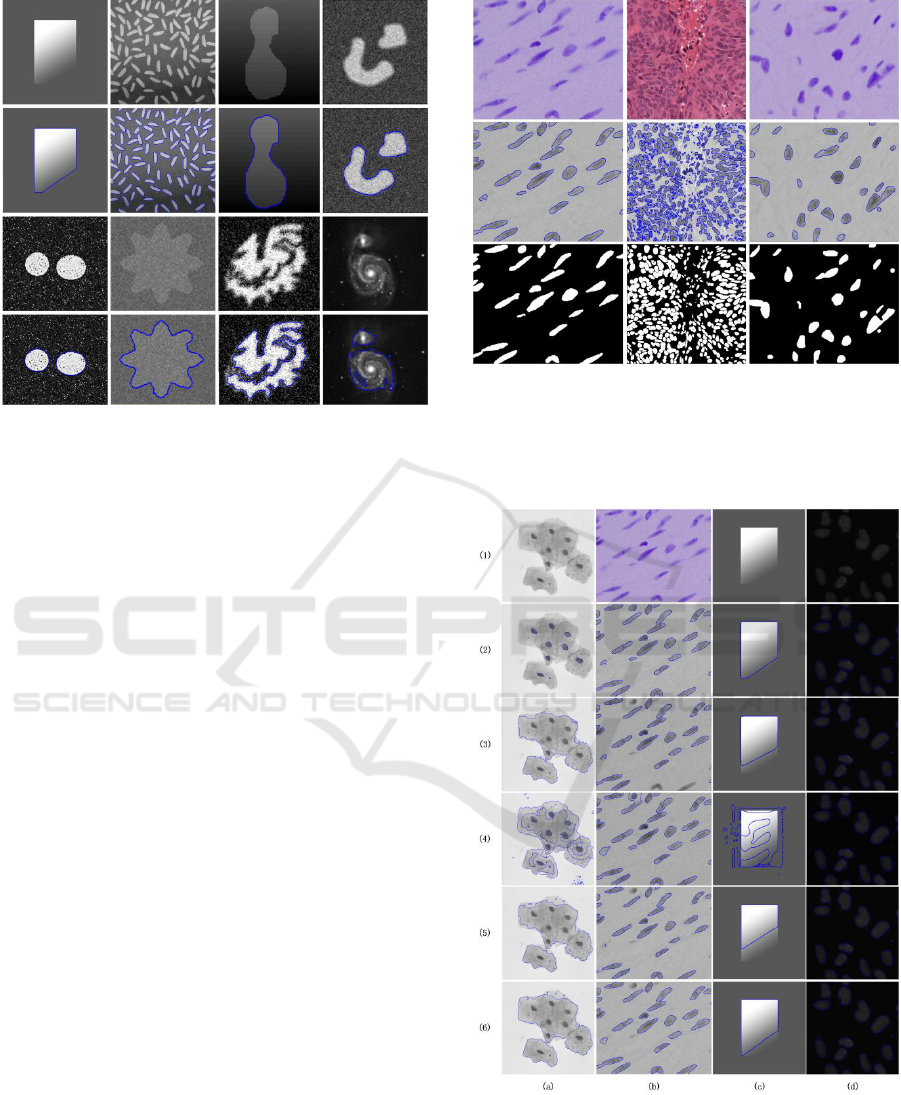
Figure 4: Segmentation results of our proposed method on
synthetic and real images. (Blue curves are the final
evolving curves.)
Similar to other existing methods, we conduct
some experiments on synthetic and real images to
prove greater generalization ability of our model in
Figure 4. Large amounts of experiments show that
our proposed model can take less time to converge
and fewer iterations to converge. For example, the
result of the first image in Figure 4 can be changed
by adjusting

and
g
. If we set
0m
,
1

and
0g
,
it reduces to the SBGFRLS model. If we only set
1

, the result is parallel to result of the LGLP
model. Moreover, the proposed method can deal
with noise images by adjusting

. The value of

is
greater, and the final contour is more smooth.
To show the robustness of our model, we still
make some experiments on colorized and multicellu
-lar images in Figure 5. Especially for the second
image in the first row, the size is
10001000
and our
model can segment it faster than other models. In
addition, we can see that the segmentation results of
the second row is extremely accurate, comparing to
ground truth in the third row. Note that the initial
contour is set as multiple balls which are equally
distributed with
30r
in the whole image.
Figure 5: Segmentation results of our proposed method on
colorized and multicellular images. Row 1: input images.
Row 2: segmentation results. Row 3: ground truth. (The
second image is one of the stage2_train data set, which is
size of
10001000
.)
Figure 6: Comparison results on images with polynuclear,
gray and multicellular, intensity inhomogeneity, and low-
contrast multicellular. Row 1: input images. Row 2: results
of the proposed method. Row 3: results of the L2S model.
Row 4: results of the RSLGD model. Row5: results of the
SBGFRLS model. Row 6: results of the LGLP model.
(Blue curves are the final evolving curves.)
A Fast Level Set Based on New Signed Pressure Force Function for Nuclei Images Segmentation
15

4.3 Performance Evaluation
From the above, the proposed model has three
advantages, including the capability of catching
multiple objects boundaries fast, dealing with noise
and intensity inhomogeneity images effectively, and
great generalization by adjusting

. In the paper, we
choose 4 different type models to make comparison
in Figure 6. They are L2S, RSLGD, SBGFRLE, and
LGLP respectively. As we see in Figure 6, images
with polynuclear, gray and multicellular, intensity
inhomogeneity, and low-contrast multicellular are
chosen to support the above advantages. In a while,
we utilize two quantitative analysis indexes, i.e. the
iterations and required CPU time of
segmentation results, to highlight the strengths
of our model in Figure 7-8.
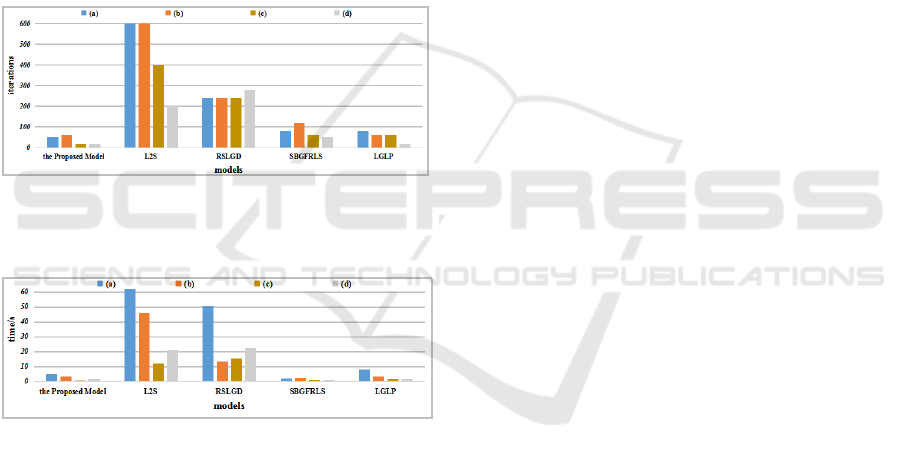
Figure 7: The iterations of different models in Figure 6.
(From left to right: the proposed model, L2S, RSLGD,
SBGFRLS, and LGLP.)
Figure 8: The CPU time of different models in Figure 6.
(From left to right: the proposed model, L2S, RSLGD,
SBGFRLS, and LGLP.)
In details, we still analyze the results of contrast
experiments in Figure 6-8. The L2S model is one of
region-based models. Even though we set a global
initial level set function, we can’t segment the whole
objects like row 3. But 1-D Legendre polynomials in
the model can efficaciously overcome intensity inho
-mogeneity. Next, the RSLGD model can combine
region and edge information by a new ESF to
capture the object boundaries as far as possible.
However, it has limitations that the gray value of
image is Gaussian distribution like row 4 and col 3.
A new region-based signed pressure force function
is proposed in the SBGFRLE model, which can
efficiently stop the contours at weak or blurred
edges, but the model can’t segment images with
intensity inhomogeneity. Finally, the LGLP model
combines L2S with SBGFRLE, and employs an
ESF to capture the object boundaries fast. But it
can’t deal with polynuclear images.
Finally, the Figure 7-8 respectively explain the
iterations and CPU time about the selected images in
Figure 6. We can obtain that the proposed model is
comparatively superior to other models.
5 CONCLUSIONS
In this paper, we has proposed a fast level set
method which combines signed pressure force
function with 1-D Legendre polynomial. To segment
polynuclear images, we set a constrained parameter
to adjust degree of convergence with regard to
signed pressure force function. Besides, we set
multiple ball contours for each image to reduce the
costly re-initialization of the previous methods and
possesses the characteristic of global segmentation.
Meanwhile, we employ an ESF to capture the edge
information and speed up the segmentation. Finally,
compared with L2S, RSLGD, SBGFRLS and LGLP,
our model not only enhances the ability of generali
-zation, but also improves the efficiency and accura
-cy of segmentation results for various nuclei images,
especially for large size images.
ACKNOWLEDGEMENTS
The work is supported by Ministry of The "ChunHui
Plan" Fund Project of The Ministry of Education
(Z2014085) and Chongqing Municipal Education
Commission Project (KJ1601210) in College of Big
Data and Intelligent Engineering, Yangtze Normal
University.
REFERENCES
Kass M, Witkin A, & Terzopoulos D. (1988). Snakes:
Active contour models[J]. International Journal of
Computer Vision, 1(4), 321-331.
Caselles V, Kimmel & R, Sapiro G. (1997). Geodesic
active contours[J]. International Journal of Computer
Vision, 22(1), 61-79.
CTISC 2019 - International Conference on Advances in Computer Technology, Information Science and Communications
16

Chan, T. F., & Vese, L. A. (2001). Active contours
without edges[J]. IEEE Transactions on Image
Processing, 10(2), 266‐277.
Li, Chunming, Xu, Chenyang, Gui, Changfeng & Fox,
M.D.. (2005). Level set evolution without re-
initialization: A new variational formulation[C].
Proceedings of the IEEE Computer Society
Conference on Computer Vision and Pattern
Recognition. 1(1), 430- 436.
Li C L C , Kao C Y , & Gore J C , et al. (2007). Implicit
Active Contours Driven by Local Binary Fitting
Energy[C]. IEEE Conference on Computer Vision &
Pattern Recognition, 1(1), 1-7.
Li C , Kao C Y , & Gore J C , et al. (2008). Minimization
of Region-Scalable Fitting Energy for Image
Segmentation[J]. IEEE Transactions on Image
Processing, 17(10), 1940-1949.
Lankton S, & Tannenbaum A. (2008). Localizing Region-
Based Active Contours[J]. IEEE Transactions on
Image Processing, 17(11), 2029-2039.
Zhang K, Song H, & Zhang L. (2010). Active contours
driven by local image fitting energy[J]. Pattern
Recognition, 43(4), 1199-1206.
Li C , Xu C , & Gui C , et al. (2011). Distance Regularized
Level Set Evolution and Its Application to Image
Segmentation[J]. IEEE Transactions on Image
Processing, 19(12), 3243-3254.
Zhang K , Zhang L , Song H , et al. (2010). Active
contours with selective local or global segmentation:
A new formulation and level set method[J]. Image and
Vision Computing, 28(4), 668-676.
Wang X F, Huang D S, & Xu H. (2010). An efficient local
Chan-Vese model for image segmentation[J]. Pattern
Recognition, 43(3), 603-618.
Dai L , Ding J , & Yang J . (2015). Inhomogeneity-
embedded active contour for natural image
segmentation[J]. Pattern Recognition, 2015, 48(8),
2513-2529.
Abdelsamea, M. M. , & Tsaftaris, S. . (2013). Active
contour model driven by globally signed region
pressure force[C]. International Conference on Digital
Signal Processing. IEEE.
Akram, F., Kim, J. H., & Choi, K. N.. (2013). Active
Contour Method with Locally Computed Signed
Pressure Force Function: An Application to Brain MR
Image Segmentation[C]. Seventh International
Conference on Image & Graphics. IEEE Computer
Society, 1(1), 154-159.
Saini K , Dewal M L , & Rohit M. (2013). Level set based
on new Signed Pressure Force Function for
Echocardiographic image segmentation[J].
International Journal of Innovation & Applied Studies,
3(2), 560-569.
Wu Z, Gurari D, & Wong J Y , et al. (2012). Hierarchical
Partial Matching and Segmentation of Interacting
Cells[C]. International Conference on Medical Image
Computing & Computer-assisted Intervention.
Springer Berlin Heidelberg, 1(1), 389-396.
Park C , Huang J Z , & Ji J X , et al. (2013). Segmentation,
Inference and Classification of Partially Overlapping
Nanoparticles[J]. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 35(3), 1-1.
Mukherjee S, & Acton S T. (2014). Region Based
Segmentation in Presence of Intensity Inhomogeneity
Using Legendre Polynomials[J]. IEEE Signal
Processing Letters, 22(3), 298-302.
Dai L, Ding J, & Yang J. (2015). Inhomogeneity-
embedded active contour for natural image
segmentation[J]. Pattern Recognition, 48(8), 2513-
2529.
Sarkar R, Mukherjee S, & Acton S T. (2015). Dictionary
Learning Level Set[J]. IEEE Signal Processing Letters,
22(11), 2034-2038.
Xing F, Xie Y, & Yang L. (2016). An Automatic
Learning-Based Framework for Robust Nucleus
Segmentation[J]. IEEE Transactions on Medical
Imaging, 35(2), 550-566.
Zheng, S. , Fang, B. , Wang, P. S. P. , Li, L. , & Gao, M..
(2016). Multi-scale B-spline level set segmenta -tion
based on Gaussian kernel equalization[C]. IEEE
International Conference on Image Processing, 1(1),
4319-4323.
Zheng S , Fang B , & Li L , et al. (2017). Automatic Liver
Lesion Segmentation in CT Combining Fully
Convolutional Networks and Non-negative Matrix
Factorization[J]. Imaging for Patient-Customized
Simulations and Systems for Point-of-Care Ultrasound,
1(1), 44-51.
Zhang, Wei, Fang, Bin, Wu, Xuegang, Qian, Jiye, Yang,
Weibin & Zheng, Shenhai. (2017). An improved
active contour model driven by region-scalable and
local Gaussian-distribution fitting energy[C].
International Conference on Security, Pattern Analysis,
and Cybernetics, 1(1), 417-422.
Zhang, Kaihua, Zhang Lei, Lam Kin-Man, & Zhang David.
(2016). A Level Set Approach to Image Segmentation
With Intensity Inhomogeneity. 1(1), 546-557.
Chen G , Chen M , & Li J , et al. (2017). Retina Image
Vessel Segmentation Using a Hybrid CGLI Level Set
Method[J]. Biomed Research International, 1(1), 1-11.
Lee C H , Soomro S , & Akram F , et al. (2017).
Segmentation of Left and Right Ventricles in Cardiac
MRI Using Active Contours[J]. Computational and
Mathematical Methods in Medicine, 1(1), 1-16.
Min H , Jia W , & Zhao Y , et al. (2018). LATE: A Level-
Set Method Based on Local Approximation of Taylor
Expansion for Segmenting Intensity Inhomogeneous
Images[J]. IEEE Transactions on Image Processing A
Publication of the IEEE Signal Processing Society,
27(10), 5016-5.31.
He, Guanghui, Yang, Guangfang, Fang, Bin & Zhang,
Wei. (2018). An Improved Local or Global Active
Contour Driven by Legendre Polynomials[C].
International Conference on Wavelet Analysis and
Pattern Recognition, 1(1), 23-28.
A Fast Level Set Based on New Signed Pressure Force Function for Nuclei Images Segmentation
17