
Trading Memory versus Workload Overhead in Graph Pattern Matching
on Multiprocessor Systems
Alexander Krause
1 a
, Frank Ebner
2 b
, Dirk Habich
1 c
and Wolfgang Lehner
1 d
1
Technische Universit
¨
at Dresden, Database Systems Group, Dresden, Germany
2
University of Applied Sciences W
¨
urzburg-Schweinfurt, Faculty of Computer Science and Business Information Systems,
W
¨
urzburg, Germany
Keywords:
Graph Processing, In-memory, Bloom Filter, Multiprocessor System, NUMA.
Abstract:
Graph pattern matching (GPM) is a core primitive in graph analysis with many applications. Efficient process-
ing of GPM on modern NUMA systems poses several challenges, such as an intelligent storage of the graph
itself or keeping track of vertex locality information. During query processing, intermediate results need to
be communicated, but target partitions are not always directly identifiable, which requires all workers to scan
for requested vertices. To optimize this performance bottleneck, we introduce a Bloom filter based workload
reduction approach and discuss the benefits and drawbacks of different implementations. Furthermore, we
show the trade-offs between invested memory and performance gain, compared to fully redundant storage.
1 INTRODUCTION
To satisfy the ever-growing computing power de-
mand, hardware vendors improve their single hard-
ware systems by providing an increasingly high de-
gree of parallelism. In this direction, large-scale sym-
metric multiprocessor (SMP) are the next parallel
hardware wave (Borkar et al., 2011). These SMP sys-
tems are characterized by each processor having the
same architecture e.g. a multicore and all multipro-
cessors share a common memory space. This SMP
type can be further classified into SMP with uniform
memory access (UMA) and SMP with non-uniform
memory access (NUMA), with the latter being the
dominant approach. Both allow all processors to ac-
cess the complete memory, but with different connec-
tivity. This is a completely different hardware ap-
proach, since former processor generations got more
performant by increasing their core frequency, lead-
ing to a higher performance at a free lunch. This effect
came to an end due to power and thermal constraints.
Thus, speedups will only be achieved by adding more
parallel units. However, these have to be utilized in an
appropriate way (Borkar et al., 2011; Sutter, 2005).
In addition to a very high number of cores, these
large-scale NUMA-SMP systems also feature main
a
https://orcid.org/0000-0002-2616-8739
b
https://orcid.org/0000-0002-4698-8232
c
https://orcid.org/0000-0002-8671-5466
d
https://orcid.org/0000-0001-8107-2775
memory capacities of several terabytes (Borkar et al.,
2011; Kissinger et al., 2014). For applications like
graph processing, this means that large graphs can
be stored completely in memory and efficiently pro-
cessed in parallel. Fundamentally, the meaning of
graphs as data structure is increasing in a wide and
heterogeneous spectrum of domains, ranging from
recommendations in social media platforms to ana-
lyzing protein interactions in bioinformatics (Paradies
and Voigt, 2017). Based on that, graph analytics is
also increasingly attractive to acquire new insights
from graph-shaped data. In this context, graph pat-
tern matching (GPM) is an important, declarative,
topology-based query mechanism and a core primi-
tive. The pattern matching problem is to find all pos-
sible subgraphs within a graph that match a given pat-
tern. The calculation of graph patterns can get pro-
hibitively expensive due to the combinatorial nature.
To efficiently compute graph patterns on such large-
scale systems, we already proposed a NUMA-aware
GPM infrastructure in (Krause et al., 2017a; Krause
et al., 2017b), which is based on a data-oriented ar-
chitecture (DORA) (Kissinger et al., 2014; Pandis
et al., 2010). As Figure 1 shows, our infrastructure
is characterized by implicitly partitioning graphs into
small partitions and each partition is placed in the lo-
cal memory of a specific NUMA node. Moreover,
we use a thread-to-data mapping, such that each local
hardware thread runs a worker. These are limited to
operate exclusively on local graph partitions. Based
on that, the calculation of pattern matching flows from
400
Krause, A., Ebner, F., Habich, D. and Lehner, W.
Trading Memory versus Workload Overhead in Graph Pattern Matching on Multiprocessor Systems.
DOI: 10.5220/0008116904000407
In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 400-407
ISBN: 978-989-758-377-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Data-oriented graph partitioning with thread as-
signment.
thread to thread depending on the data being accessed.
Our previous work shows good scalability, whereby
the graph partitioning has a high performance impact.
This is remedied by a set of indicators, which we use
to select the optimal partitioning strategy for a given
graph and workload in (Krause et al., 2017a).
Our Contribution. DORA enables us to fully uti-
lize all cores to efficiently process a pattern query in
a highly parallel way. However, since we need to ex-
plicitly exchange intermediate results between work-
ers, our whole approach depends on how we store
the graph. If we only consider outgoing edges in a
directed graph, we cannot always determine exactly
to which partition (workers) the intermediate results
have to be sent for further processing. In this case,
we have to send them to all workers using a broad-
cast. This can be mitigated by also storing incom-
ing edges as full redundancy. The consequence is
doubled memory consumption, but we can send uni-
casts, because target vertices can be directly looked
up. We propose to employ a Bloom filter based solu-
tion, which reduces broadcasts to a couple of unicasts,
while only requiring a fraction of the memory over-
head compared to full redundancy. Thus, our trade off
for memory vs. workload overhead remains bearable.
Outline. This paper is structured as follows: In
section 2, we briefly introduce our graph data model
including an illustration of GPM. Then, we introduce
our Bloom filter-based approach to efficiently trade
memory versus workload overhead for GPM on large-
scale NUMA-SMP systems in Section 3. Based on
that, Section 4 describes selected evaluation results.
Finally, we close the paper with related work and a
short conclusion in Sections 5 and 6.
2 DATA MODEL AND PATTERN
MATCHING
Within this paper, we focus on edge-labeled multi-
graphs (ELMGs) as a general and widely employed
graph data model (Pandit et al., 2007; Otte and
Rousseau, 2002). An ELMGs G(V,E, ρ, Σ, λ) con-
sists of a set of vertices V, a set of edges E, an inci-
dence function ρ : E → V ×V , and a labeling function
λ : E → Σ that assigns a label to each edge. Hence,
ELMGs allow any number of labeled edges between
a pair of vertices, with RDF being a prominent exam-
ple (Decker et al., 2000). This model does not im-
pose any limitation, since e.g. property graphs can
also be expressed as directed ELMGs through intro-
ducing additional vertices and edges for properties.
Storing a graph can be done manifold. One of
the most intuitive and straightforward ways is to store
all outgoing edges of a vertex as an edge list, which
we call outgoing edge storage (OES). This way, the
topology of the graph can be represented precisely
and lossless. To conform with DORA, we store all
outgoing edges of one vertex within the same parti-
tion. Measures for balanced partitioning are neces-
sary and applied, but out of scope of this work.
As mentioned in Section 1, GPM is a declara-
tive topology-based querying mechanism. The query
is given as a graph-shaped pattern and the result is
a set of matching subgraphs (Tran et al., 2009). A
well-studied mechanism for expressing such query
patterns are conjunctive queries (CQs) (Wood, 2012),
which decompose the pattern into a set of edge pred-
icates each consisting of a pair of vertices and an
edge label. Following this, the example query (A) →
(RedVertex) → (B) is decomposed into the conjunc-
tive query {(V
A
) → (V
red
), (V
red
) → (V
B
)}. Answer-
ing this query is easy using OES for Figure 1, since
we only need to lookup all matches for V
A
first and
do the same for all found (V
red
) subsequently. This
is done by sending a single unicast message between
two workers, communicating the intermediate results.
This is straightforward, since the OES is partitioned
by the vertex ids, which can be directly looked up to
find their corresponding partition. Adding edge labels
speeds up this process, as they increase the queries se-
lectivity. However, reversing one of the edges, e.g. as
in (A) → (RedVertex) ← (B), the process gets com-
plicated. The first step remains the same, but finding
all vertices (V
B
) now requires a broadcast message
targeting all partitions. The OES does not allow di-
rect lookup of target vertices, thus we need to activate
all workers to scan their partitions, if there is a (V
B
),
which has (V
red
) as target vertex. Hence, the work-
ers processing the grey and yellow partition perform
unnecessary work which should be avoided.
Trading Memory versus Workload Overhead in Graph Pattern Matching on Multiprocessor Systems
401

3 TRADING MEMORY VERSUS
WORKLOAD OVERHEAD
Processing GPM on NUMA-SMP systems poses sev-
eral challenges. With the data partitioning being a
prominent example, another obstacle is the available
vertex locality information, based on the edge stor-
age. In our previous work (Krause et al., 2017b),
we have shown the influence of incomplete vertex lo-
cality information, due to OES. We found, that an-
swering queries with backward edges results in the
activation of all workers (i.e. sending a broadcast),
to find out, which partition actually contains the re-
quested vertices.The resulting workload overhead can
have significant performance impact and should thus
be avoided; i.e. the reduction of messages in the sys-
tem is highly desirable. A straightforward solution
for this problem is to simply store full redundancy,
i.e. reversing all edges and store them partitioned by
the target vertex as incoming edges. This incoming
edge storage (IES) adds a twofold storage overhead,
but can increase the system performance dramatically.
That is, since workers, which do not contain a re-
quested vertex from a broadcast, do not get stalled
with excess calls and can perform their actual work in
time. However, when the stored graph grows or when
there is a tighter memory budget, this approach is not
feasible anymore. The consequence is to find a trade
off between the invested memory for the gained per-
formance. There is one direct fit for this requirement:
A Bloom filter. The probabilistic data structure can
be scaled in its size, which implicates varying accu-
racy and thus allows us to trade invested memory for
workload.
Bloom Filter Design Aspects. Instead of storing
each element completely and as-is, requiring large
amounts of storage capacity, the Bloom filter refers
to a few bits to remember a vertex’ presence. Filling
is performed by a hash function, which is applied to
the vertex id, with the result denoting the slot number
into a bitfield, denoting the bit to set to 1. To check
whether a vertex id is present, its hash is calculated
and the bitfield is checked, whether it contains a 1 or 0
at the index given by the hash. By not fully describing
each vertex, this represents a probabilistic data struc-
ture with a false positive rate, i.e. returning true, even
if a vertex is not present. Yset, false negatives, i.e. re-
turning a false for a vertex which is actually present,
are forbidden. Due to collisions, using just one bit
per vertex, usually yields false positive rates above
an acceptable level. Hence implementations use more
than one hash per element, where H
0
i
(x)6=
!
H
0
j
(x) ∀x
and i 6= j. For each hash, a 1 is stored within the cor-
responding bit. When querying, the element might
exist, if all bitfield indices contain a 1. The false pos-
itive rate p thus depends on the number K of hashes
used per vertex, and the number of bits M within the
bitfield. The approximate number of bits required for
storing N vertices at a desired false positive rate, is
given by (Bloom, 1970; Broder and Mitzenmacher,
2003), cf. (1). This yields a space requirement of
≈10 bits per vertex for a false positive rate of 1 %,
which is much less compared to fully redundant stor-
age. Similar rules hold true for the optimal number
of hashes, (Broder and Mitzenmacher, 2003), see (2).
With the number of stored bits being dynamic, we can
adjust the Bloom filter size to yield a reasonable false
positive rate.
M ≈ −1.44N log
2
(p) . (1)
K =
M
N
ln2 ≈ −1.44 ln(2)log
2
(p) . (2)
The computational cost of the Bloom filter mainly de-
pends on the performance of the hash algorithms, con-
verting arbitrary data into a numeric value, uniformly
throughout the whole range, that is, the size of the bit-
field. While 64 bit unsigned integer vertex ids already
are numeric values, ids can not be used as-are, since
the bitfield will be much smaller than 2
64
bits. Yet, a
hash function for this kind of input data is much sim-
pler, as it just needs to distribute all potential vertex
ids uniformly among the available bitfield slots. This
is commonly achieved by multiplying the id x with
some number a
i
, limiting the result to the number of
slots using the modulo operator:
H
0
i
(x) = y = a
i
· x (mod M), x ∈ N, a
i
∈ N
>0
. (3)
However, this operator is known to be very costly
(Granlund, 2017). Thus we exploit the residue class
ring property (4). For 64 bit unsigned integer ver-
tex ids, which are of base 2, the last k digits of (x)
2
are given by applying a bitmask, or bitwise and, of
(2
k
− 1) to (x)
2
. Following this approach, we can
alter (3) by replacing the modulo operator with bit-
wise and while selecting prime numbers for a
i
, since
they yield best uniformity results (Hull and Dobell,
1962). Therefore, we limit our Bloom filter sizes to
2
k
, k ∈ N and use (5) as our hash algorithm, which we
call PrimeHash henceforth.
(x)
base
(mod base
k
) = last k digits of (x)
base
. (4)
H
0
i
(x) = y = (a
i
· x) ∧ (M − 1) . (5)
Besides returning false positives, Bloom filters suf-
fers from additional drawbacks that need to be con-
sidered: As only single bits are stored, collisions can
not be tracked, and vertices can not be deleted from
the filter. For dynamic graphs, where many deletions
occur, the false positive rate might reach unacceptable
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
402

levels over time. To overcome collisions ambiguities,
the counting Bloom filter stores the number of ele-
ments contributing to each slot. This enables deletion
by decreasing the corresponding number, but requires
additional memory to store counters instead of bits.
Similar to the missing support for deletion, is the lack
of runtime scalability. The more vertices are added to
the filter, the more bits are set to 1. Eventually, all bits
will be set and the filter is useless. As the Bloom fil-
ter does not store the vertices themselves, growing is
not supported by the data structure on its own, but re-
quires re-scanning the whole graph, rehashing all ver-
tices. To reach an acceptable false positive rate for a
given graph, the Bloom filters size, and thus the num-
ber of to-be-added vertices, must be known before-
hand. Scalable Bloom filters can mitigate this issue,
but within this paper we concentrate on static graphs
and static Bloom filters, to reduce complexity. This
does not limit the applicability of our approach, since
static and dynamic graphs share the same messaging
procedure, and processing GPM on dynamic graphs
would equally benefit from our optimization. A scal-
able Bloom filter with a dynamic graph would only
add to computational complexity, but not to the mes-
saging issue, and is thus ignored.
4 EVALUATION
Our developed GPM engine is a research prototype,
which builds upon the DORA, targeting NUMA-SMP
systems as mentioned in Section 1. We have tested
our GPM engine against three different graphs. One
is a bibliographical network, the second represents a
social network and the third graph stands for a protein
network, where the three are called biblio, social and
uniprot respectively henceforth. All three graphs are
generated with gMark (Bagan et al., 2017) to consist
of approx. 1 M edges each. For our experiments, we
store the graphs both with OES and fully redundant
(OES+IES), as described in Sections 2 and 3. Our
evaluation hardware consists of a four socket NUMA
system, each equipped with an Intel(R) Xeon(R) Gold
6130 CPU @ 2.10GHz, resulting in 128 hardware
threads with a total of 384 GB of main memory. With
this system, we want to examine the messaging be-
havior between a large number of workers, even if its
main memory is a bit over-provisioned for the gen-
erated datasets. This section is structured as follows:
First, we want to emphasize the necessity of a care-
ful Bloom filter design. Second, we show the benefits
and drawbacks of both fully redundant storage versus
the Bloom filter optimized storage. Third, we conduct
extensive experiments and run the example queries
against the aforementioned storage settings, with and
without an additionally applied Bloom filter in differ-
ent parts of our GPM engine. To underline the impor-
tance of an appropriate Bloom filter design, we show
its read/write performance in Figure 2. Figure 2(a)
shows the write results for our testing machine. As
can be seen, the counting filter from Section 3 yields
the same insertion performance as storing only one bit
in a larger type, since their points almost overlap for
32 bit or 64 bit data types. Using packed data storage,
where each hashed bit is stored using an actual bit
within a larger scalar value, proves to be the fastest
storage solution. This is most likely due to reduced
storage requirements, fitting the internal caches of the
CPU. Figure 2(b) proves the superiority of our bitwise
and based PrimeHash against the traditional modulo
operator. In terms of fairness, we ran our experi-
ments for the modulo operator against Bloom filters
using the same size as required for PrimeHash (2
x
,
see Eq. (4)) as well as the exactly calculated size ac-
cording to Eq. 1. The figure shows, that using bitwise
and clearly outperforms the modulo variants within
both scenarios: always calculating all hash functions
according to Eq. (2), or returning after the first false
(early-out).
For our graph related experiments, we have used
the partitioning strategies as explained in (Krause
et al., 2017a). From that paper, we have chosen
HashVertices, RoundRobinVertices and Multilevel k-
Way partitioning. In summary, the first two parti-
tion the graph following their names and the k-Way
partitioning is a sophisticated graph partitioning al-
gorithm, which first partitions the graph very coarse
grained but later refines the result in subsequent steps.
In this paper, we use the METIS 5.1 implementation
of that algorithm (Karypis and Kumar, 1998). Fur-
thermore, we have chosen two different graph pat-
terns for our analysis. The query Q1 forms a rectan-
gle consisting of four vertices and four edges and the
query Q2 represents a V shaped pattern consisting of
five vertices and four edges. Both queries have a dif-
ferent amount of backward edges at significant eval-
uation steps to emphasize their impact. This leads to
diverse communicational behavior, which allows us
to show the effect of both full redundancy and Bloom
filter usage standalone and in combination.
Figure 3(a) depicts the general memory invest-
ment for the previously mentioned improvements.
The figure shows the relative storage overhead for full
redundancy, which is obviously always twice as much
as OES, compared to the standard storage. Adding a
Bloom filter to the raw storage does not add much
in terms of memory needed, however its performance
gain can be remarkable. Figure 3(b) shows the result-
Trading Memory versus Workload Overhead in Graph Pattern Matching on Multiprocessor Systems
403

0
20
40
60
80
2
16
2
17
2
18
2
19
2
20
2
21
2
22
2
23
2
24
time [ms]
BitSet size [number of bits]
Counting 64
Single 64
Counting 32
Single 32
Single 8
Packed 8
Packed 32
Packed 64
(a) Insert 5 million entries.
0
0.5
1
1.5
2
4 6 8 10 12 14 16
time [s]
Bits per item [number of bits]
BF AND (e-out)
BF MOD1 (e-out)
BF MOD2 (e-out)
BF AND (all)
BF MOD1 (all)
BF MOD2 (all)
(b) Query 1 million items.
Figure 2: Time to perform different actions, based on the Bloom filter storage strategy (left) and comparing bitwise and [BF
AND] vs. the modulo operator [BF MOD1/2] (right). While [BF MOD1] uses the size required by Eq. (4), [BF MOD2] refers
to the size from Eq. (1) instead.
(a) Relative storage overhead.
(b) Relative query performance for Q1.
Figure 3: Invested memory vs. gained performance for full
redundancy against a Bloom filter within the data partitions,
M = 2
20
, k-Way partitioning.
ing query run times for all storage strategies. The raw
storage is only the slowest and adding redundancy or a
Bloom fitler increases the performance. Interestingly,
for the Biblio use case, the Bloom filter outperforms
even the redundant storage. The reason is, that the
Bloom filter can sort out edge requests for target ver-
tices, that are not stored in the partition, which is not
covered by redundant storage.
When implementing the Bloom filter, we can do
that on multiple locations. Obvious candidates are the
data partitions themselves, which makes the Bloom
filter behave more like a secondary index. By doing
this, the system still needs to activate all workers to
find out, if a partition contains a requested vertex. On
the other hand, we still exploit all cores to perform
the filtering process in parallel. A second possibility
is to place the Bloom filter together with the partition-
ing information. This allows us to directly check, if a
certain partition possibly contains a requested vertex.
The routing based workload reduction can give an-
other performance increase as shown in Figure 4(a),
since workers are not unnecessarily activated. How-
ever, looking up target partitions is an inherently se-
rial code segment. Thus, iterating over all partition re-
lated Bloom filters leads to increased local overhead,
which linearly increases with the amount of partitions
in the system.
Besides varying the Bloom filter location, we can
also swap the underlying partitioning. Figure 4(b)
depicts the relative query runtime for routing based
workload optimization using the RoundRobinVertices
(RRV) partitioning strategy. We observe completely
different query performance for both the redundant
and Bloom filter supported query execution. In addi-
tion, neither the RRV nor the k-Way partitioning strat-
egy yield globally optimal results, which supports our
findings from previous work (Krause et al., 2017a).
Yet, the Bloom filter approach increases the query
performance for both underlying partitionings.
After showing the performance gain for Q1, we
now discuss selected results for Q2 in Figure 4. As
for Q1, we achieve a performance gain with both the
redundant storage as well as the Bloom filter employ-
ment. However, here we see a significant difference
between the two, at least for the Uniprot graph. We
identified, that an extraordinarily high amount of in-
termediate results occurs right before evaluating the
backward edge and thus, the aforementioned serial
checking of Bloom filter becomes a bottleneck.
Based on these observations, we can state that em-
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
404
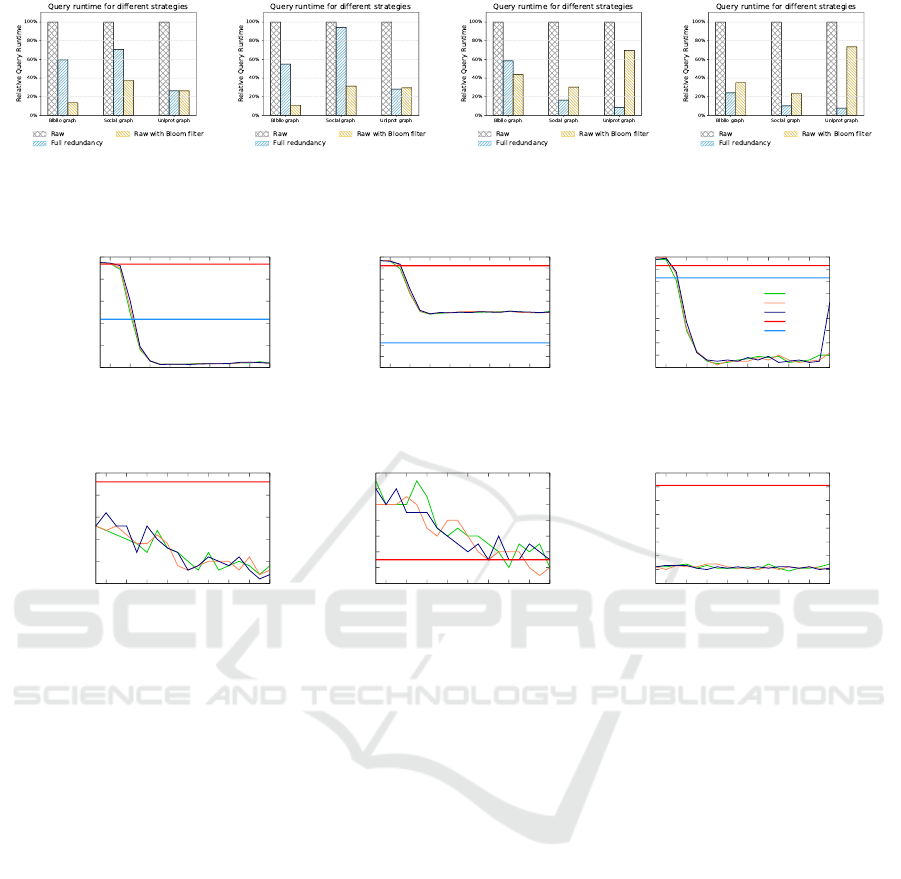
(a) Q1, k-Way partitioning. (b) Q1, RRV partitioning. (c) Q2, k-Way partitioning. (d) Q2, RRV partitioning.
Figure 4: Relative query performance for different partitioning strategies using the routing based workload reduction, M = 2
20
.
1000
1500
2000
2500
3000
3500
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
Hash partitioning
(a) Bib, Q1, BC
0
100
200
300
400
500
600
700
800
900
1000
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
RRV partitioning
(b) Bib, Q2, BC
90
100
110
120
130
140
150
160
170
180
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
RRV partitioning
7 Hashes
8 Hashes
9 Hashes
Unoptimized
Full Redundancy
(c) Social, Q1, BC
675
680
685
690
695
700
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
RRV partitioning
(d) Uni, Q2, UC
192
194
196
198
200
202
204
206
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
Hash partitioning
(e) Bib, Q2, UC
110
120
130
140
150
160
170
180
190
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
Hash partitioning
(f) Social, Q1, UC
Figure 5: Query Performance with varying Bloom filter parameters, Bloom filter implemented in the data partitions. The
baseline denotes the performance without a Bloom filter. BC = Broadcasts with ’OES’ as Unoptimized, UC = Unicasts with
’Fully redundant’ as Unoptimized
ploying a fixed sized Bloom filter can help to improve
query performance with low memory overhead. How-
ever, as the performance of the Bloom filter varies
with its size M, we conducted various experiments
with both partition and routing based Bloom filter im-
plementations. For the experiments in Figure 5, we
examined both queries on all mentioned data sets. We
have tested the impact of a different number of hash
functions against the baseline, where no Bloom filter
was used and thus always all workers need to be ac-
tivated. We will only present selected experiments,
due to the large amount of possible experiments. Pre-
sented runtimes are the average of 10 runs, without
the fastest and the slowest runtime. The first row of
Figures 5 and 6 shows selected experiments for the
raw storage with only outgoing edges, and the second
row applies our Bloom filter on top of the fully redun-
dant storage, to show that combining both strategies
can improve our performance even further. Because
of the varying runtime between the testing queries and
on different graphs, we scaled the Y-axis accordingly
for every experiment in Figures 5 and 6.
All figures from Figure 5, except Figure 5(e),
clearly show the desired results. That is, the big-
ger the Bloom filter, the bigger is the performance
benefit. Increasing the Bloom filter size is indirectly
proportional to the expected false positive rate, thus
leading to less unnecessary work. In detail, Fig-
ure 5(b) behaves like anticipated. Adding a Bloom
filter will increase the performance to allow query
runtimes somewhere between the raw storage and the
fully redundant storage. On top of that, Figures 5(a)
and 5(c) show an improved performance even beyond
the fully redundant storage. The same holds true for
Figures 5(d) and 5(f). Applying our Bloom filter tech-
nique on top of the fully redundant storage leads to an
additional performance boost, since the Bloom filter
acts as a secondary index structure. By blooming all
target vertices for every source vertex in a partition,
the Bloom filter can most certainly reject requests for
edges with a target vertex, which is not present in the
respective partition.
Figure 5(e) is a special case. For smaller Bloom
filters, the systems performance is slower than us-
Trading Memory versus Workload Overhead in Graph Pattern Matching on Multiprocessor Systems
405

0
500
1000
1500
2000
2500
3000
3500
4000
4500
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
RRV partitioning
(a) Bib, Q1, BC
0
200
400
600
800
1000
1200
1400
1600
1800
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
HV partitioning
7 Hashes
8 Hashes
9 Hashes
Unoptimized
Full Redundancy
(b) Bib, Q2, BC
50
100
150
200
250
300
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
RRV partitioning
(c) Social, Q1, BC
690
695
700
705
710
715
720
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
RRV partitioning
(d) Uni, Q2, UC
600
610
620
630
640
650
660
670
680
690
700
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
KWay partitioning
(e) Bib, Q2, UC
110
120
130
140
150
160
170
180
190
2
14
2
16
2
18
2
20
2
22
2
24
2
26
2
28
2
30
Query runtime [ms]
Bloom Filter size [bit]
Hash partitioning
(f) Social, Q1, UC
Figure 6: Query Performance with varying Bloom filter parameters, Bloom filter implemented with the partitioning infor-
mation. The baseline denotes the performance without a Bloom filter. BC = Broadcasts with ’OES’ as Unoptimized, UC =
Unicasts with ’Fully redundant’ as Unoptimized
ing the raw storage. Although the query runtime is
consistently decreasing, it barely reaches the baseline
performance, where no Bloom filter is used. This be-
havior can be explained with the amount of broadcasts
in the system, when only a small number of partitions
contains actual data. Since the Bloom filter is only
active, after the messages have been sent, we still see
the same amount of messages in the system and the
overhead of checking the Bloom filter is added on top
of it.
For better comparability, Figure 6 shows the same
experiments as Figure 5, but with the adjusted Bloom
filter location. Most surprising is the observation, that
avoiding messages is not generally better. For exam-
ple, the experiments of Figures 5(d) and 6(d) show a
better performance, when messages are filtered out in
parallel, instead of avoiding them; the same holds for
Figures 5(e) and 6(e) respectively. This effect can be
explained with the large serial code segment, which
is executed, whenever the Bloom filter is probed. On
the other hand, the experiments in Figures 6(a) to 6(c)
greatly benefit from the reduced message load. As for
Figure 6(f), we can clearly see that there is an optimal
Bloom filter size, after which the performance drops,
possibly reasoned by the bigger bitfields, which get
less cache friendly.
5 RELATED WORK
Graph processing is a wide field with continuously
ongoing research. Because of the plethora of use
cases, many systems are built to solve a specific prob-
lem. A comparable system might be Pregel+ (Yan
et al., 2015), which was considered as the fastest
graph engine (Lu et al., 2014). In that system, ev-
ery worker is an MPI process and exchanges mes-
sages. Pregel+ leverages vertex mirroring to distribute
workload for improved performance, which is orthog-
onal to our approach of reducing workload. In our
evaluation, we showed that redundancy introduces a
huge memory overhead for the achieved performance,
compared to our Bloom filter approach. A more re-
cent system is Turbograph++ (Ko and Han, 2018),
which distributes vertices and edges among multi-
ple machines, where each machine stores the data
on disk. The main difference between our system
and TurboGraph++ is our processing model. Because
of the inherent messaging, our model resembles a
streaming engine, where the data flows from one op-
erator to the next, where invalid intermediate results
get pruned on the fly. The authors of (Neumann and
Weikum, 2009) use a Bloom filter to avoid construct-
ing full semi-join tables on RDF data graphs, whereas
our approach uses a Bloom filter to completely elimi-
nate the need to touch a whole data partition.
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
406

6 CONCLUSION
In this paper we have presented measures for trad-
ing storage overhead for workload reduction. Our
key findings were, that despite being more accu-
rate, fully redundant storage does not yield propor-
tional performance gain, compared to the memory in-
vested. We could show in our evaluation, that our
hand tuned Bloom filter approach can save a tremen-
dous amount of main memory and still provide rea-
sonable speedups. Considering the huge experimen-
tal space, we envision to continue this research and
combine these findings with (Krause et al., 2017a),
to built an adaptive system, which can adapt both the
partitioning and the employed Bloom filter to achieve
optimal performance.
REFERENCES
Bagan, G., Bonifati, A., Ciucanu, R., Fletcher, G. H. L.,
Lemay, A., and Advokaat, N. (2017). gMark:
Schema-driven generation of graphs and queries.
IEEE Transactions on Knowledge and Data Engineer-
ing, 29(4).
Bloom, B. H. (1970). Space/time trade-offs in hash coding
with allowable errors. Communications of the ACM,
13(7).
Borkar, S. et al. (2011). The future of microprocessors.
Commun. ACM, 54(5).
Broder, A. Z. and Mitzenmacher, M. (2003). Survey: Net-
work applications of bloom filters: A survey. Internet
Mathematics, 1(4).
Decker, S., Melnik, S., van Harmelen, F., Fensel, D., Klein,
M. C. A., Broekstra, J., Erdmann, M., and Horrocks,
I. (2000). The semantic web: The roles of XML and
RDF. IEEE Internet Computing, 4(5).
Granlund, T. (2017). Instruction latencies and
throughput for AMD and Intel x86 processors.
https://gmplib.org/˜tege/x86-timing.pdf.
Hull, T. E. and Dobell, A. R. (1962). Random Number Gen-
erators. SIAM Review, 4.
Karypis, G. and Kumar, V. (1998). A fast and high quality
multilevel scheme for partitioning irregular graphs.
Kissinger, T., Kiefer, T., Schlegel, B., Habich, D., Molka,
D., and Lehner, W. (2014). ERIS: A numa-aware in-
memory storage engine for analytical workload. In In-
ternational Workshop on Accelerating Data Manage-
ment Systems Using Modern Processor and Storage
Architectures - ADMS, Hangzhou, China, September
1.
Ko, S. and Han, W. (2018). Turbograph++: A scalable and
fast graph analytics system. In Proceedings of the In-
ternational Conference on Management of Data, SIG-
MOD Conference, Houston, TX, USA, June 10-15.
Krause, A., Kissinger, T., Habich, D., Voigt, H., and Lehner,
W. (2017a). Partitioning strategy selection for in-
memory graph pattern matching on multiprocessor
systems. In Euro-Par 2017: Parallel Processing -
23rd International Conference on Parallel and Dis-
tributed Computing, Santiago de Compostela, Spain,
August 28 - September 1, Proceedings.
Krause, A., Ungeth
¨
um, A., Kissinger, T., Habich, D., and
Lehner, W. (2017b). Asynchronous graph pattern
matching on multiprocessor systems. In New Trends
in Databases and Information Systems - ADBIS 2017
Short Papers and Workshops, AMSD, BigNovelTI,
DAS, SW4CH, DC, Nicosia, Cyprus, September 24-
27, Proceedings.
Lu, Y., Cheng, J., Yan, D., and Wu, H. (2014). Large-scale
distributed graph computing systems: An experimen-
tal evaluation. PVLDB, 8(3).
Neumann, T. and Weikum, G. (2009). Scalable join pro-
cessing on very large RDF graphs. In Proceedings of
the ACM SIGMOD International Conference on Man-
agement of Data, Providence, Rhode Island, USA,
June 29 - July 2.
Otte, E. and Rousseau, R. (2002). Social network analysis:
a powerful strategy, also for the information sciences.
J. Information Science, 28(6).
Pandis, I., Johnson, R., Hardavellas, N., and Ailamaki, A.
(2010). Data-oriented transaction execution. PVLDB,
3(1).
Pandit, S., Chau, D. H., Wang, S., and Faloutsos, C. (2007).
Netprobe: a fast and scalable system for fraud detec-
tion in online auction networks. In Proceedings of the
16th International Conference on World Wide Web,
Banff, Alberta, Canada, May 8-12.
Paradies, M. and Voigt, H. (2017). Big graph data ana-
lytics on single machines - an overview. Datenbank-
Spektrum, 17(2).
Sutter, H. (2005). The free lunch is over: A fundamental
turn toward concurrency in software. Dr. Dobb’s jour-
nal, 30(3).
Tran, T., Wang, H., Rudolph, S., and Cimiano, P. (2009).
Top-k exploration of query candidates for efficient
keyword search on graph-shaped (RDF) data. In Pro-
ceedings of the 25th International Conference on Data
Engineering, ICDE, March 29 - April 2, Shanghai,
China.
Wood, P. T. (2012). Query languages for graph databases.
SIGMOD Record, 41(1).
Yan, D., Cheng, J., Lu, Y., and Ng, W. (2015). Effec-
tive techniques for message reduction and load bal-
ancing in distributed graph computation. In Proceed-
ings of the 24th International Conference on World
Wide Web, Florence, Italy, May 18-22.
Trading Memory versus Workload Overhead in Graph Pattern Matching on Multiprocessor Systems
407
