
Visual Predictive Control of Robotic Arms with Overlapping Workspace
E. Le Fl
´
echer
1,2 a
, A. Durand-Petiteville
3
, V. Cadenat
1,2
and T. Sentenac
1
1
CNRS, LAAS, 7 Avenue du Colonel Roche, F-31400 Toulouse, France
2
Univ. de Toulouse, UPS, F-31400, Toulouse, France
3
Mechanical Department of Federal University of Pernambuco (UFPE), Recife, Brazil
Keywords:
Agricultural Robotics, Multi-arms, Non-linear Model Predictive Control, Image based Visual Servoing.
Abstract:
This paper deals with multi-arms fruits picking in orchards. More specifically, the goal is to control the arms
to approach the fruits position. To achieve this task a VPC strategy has been designed to take into account
the dynamic of the environment as well as the various constraints inherent to the mechanical system, visual
servoing manipulation and shared workspace. Our solution has been evaluated in simulation using on PR2
arms model. Different models of visual features prediction have been tested and the entire VPC strategy has
been run on various cases. The obtained results show the interest and the efficiency of this strategy to perform
a fruit picking task.
1 INTRODUCTION
To meet the increasing food demands from a grow-
ing world population, agriculture will need to double
its production by 2050. Alternatively, it will need to
reduce its environmental impact to fight against cli-
mate change and avoid to harm soils. Among the so-
lutions presented in (Foley et al., 2011; Grift et al.,
2008), robotics has been designated as one of the most
promising strategies.
Agriculture robotics may operate in various envi-
ronments such as open fields, orchards, green houses,
... In this work, one focuses on robots perform-
ing weeding, spraying, trimming, or harvesting in
orchards. The autonomous achievement of any of
these tasks requires the same capacities for the robotic
system: (i) autonomously navigate in an orchard;
(ii) detect and localize a set of natural landmarks
of interest; (iii) approach the landmarks with some
robotic manipulators; (iv) manipulate/interact with
the landmarks of interest without damaging them. Af-
ter addressing the autonomous navigation problem in
(Durand-Petiteville et al., 2017; Le Flecher et al.,
2017), the focus is now on the landmark approach
problem when considering a couple of robotic ma-
nipulators embedded on a mobile platform. This
topic has already been addressed during the design
of systems harvesting cucumbers (Van Henten et al.,
a
https://orcid.org/0000-0002-2683-8675
2003) or tomatoes (Zhao et al., 2016b). Despite
the promising results, the harvesting efficiency needs
to be increased to meet the viability demand from
farmers (Zhao et al., 2016a). To do so, one of the
most adopted approach consists of embedding several
robotics arms on the mobile platform, as it is done
in (Zhao et al., 2016a) for a melon harvester. How-
ever, it is pointed in (Vougioukas et al., 2016) that
fruits are not uniformly distributed on commercial or-
chards trees. Indeed, to maximize the fruits accessi-
bility, growers use specific trees with high fruits den-
sity, thus facilitating the manual harvesting. For this
reason, during the design of a harvesting system, it
seems then interesting to consider the use of several
arms whose workspace overlap. Thus, even if the
arms do not collaborate to manipulate one single ob-
ject, they share a common workspace. It is then possi-
ble to use several arms to pick fruits in the same high
density area, which decreases the overall harvesting
time.
Regarding the control of the robotics arms, it
seems interesting to focus on reactive controllers.
Thus, when considering the harvesting problem, a tree
is a highly dynamic environment because of the flex-
ibility of the branches and the weight of the fruits:
each time a fruit is harvested, the local distribution of
fruits and branches is modified. It is then proposed
to use an image based visual servoing (IBVS) scheme
for its reactive capabilities (Chaumette and Hutchin-
son, 2006). This kind of controller will track the fruit
130
Flécher, E., Durand-Petiteville, A., Cadenat, V. and Sentenac, T.
Visual Predictive Control of Robotic Arms with Overlapping Workspace.
DOI: 10.5220/0008119001300137
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 130-137
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of interest and use its coordinates in the image to con-
trol the arm. However, IBVS schemes working in the
image space, they do not provide any guarantee re-
garding the trajectory of the camera in the workspace.
This represents a major issue when considering arms
sharing a common workspace. A well adopted solu-
tion to take into account constraints on position, ve-
locity, or workspace is the model predictive control
scheme. Indeed, when minimizing the cost function,
the solver can deal with numerous constraints (Diehl
and Mombaur, 2006). Thus, to obtain a reactive con-
troller dealing with constraints, it is proposed to de-
sign an IBVS-based NMPC (nonlinear model predic-
tive control) controller, also named Visual Predictive
Control (VPC). For this particular case, the cost func-
tion is defined as the error between the image coordi-
nates of the visual features representing the landmark
of interest at the current pose and the desired one.
Similar control schemes have been already pro-
posed. For example, in (Allibert et al., 2010) several
prediction models are used to simulate the control of
a 6 DOF camera subject to visibility constraints. In
(Sauvee et al., 2006), the designed controller deals
with torques, joints and image constraints and is eval-
uated in simulations. In (Hajiloo et al., 2015) an
IBVS-based MPC controller using a tensor product
model is developed. It also takes into account actua-
tors limitations and visibility constraints.
In this paper, it is proposed to extend the VPC
case to the control of two arms sharing a common
workspace. Thus, in addition to drive the two end-
effectors to their desired pose using the image space,
the controllers have to guarantee the non-collision be-
tween both arms.
A non-linear predictive control strategy to perform
a reactive control based on IBVS method is simulated
on a robot equipped of multiple arms with eye-in-
hand cameras. Each arm needs to achieve separate
tasks sharing the same workspace. These tasks are
subject to constraints such as the restricted field of
view, the kinematic (joints limits in position and ve-
locity) but also the self collision constraints.
The paper is organized as follows. In section II
the robot model to estimate the location of visual fea-
tures is defined. In section III, the control strategy is
explained, as well as the cost function described and
the diverse constraints designed. Section IV is dedi-
cated to the simulation results obtained while section
V summarizes and develops the expectations for the
future.
2 MODELING
In this section, one first focuses on the modeling of
the system, i.e., the robotic arms, the cameras and the
targets. Then, two models to predict the visual feature
coordinates of a point are presented. One ends with a
discussion regarding the viability of these models for
the visual predictive control problem.
2.1 System Modeling
The robotic system considered in this work is com-
posed of n
a
identical arms, each of them contain-
ing m
q
revolute joints. A camera is attached to the
end effector of each arm. To model, the system,
let us first define a global frame F
b
= (O
b
,x
b
,y
b
,z
b
)
attached to the system base. Moreover, n
a
frames
F
c
i
= (O
c
i
,x
c
i
,y
c
i
,z
c
i
), with i ∈ [1, ...,n
a
], are used to
represent the pose of the camera attached to the i
th
arm.
One denotes q
i j
and ˙q
i j
, with j ∈ [1,...,m
q
],
respectively the angular position and velocity of
the j
th
joint of the i
th
arm. Thus, for the i
th
arm, one obtains the configuration vector Q
i
=
[q
i1
,q
i2
,...,q
im
q
]
T
and the control input vector
˙
Q
i
=
[ ˙q
i1
, ˙q
i2
,..., ˙q
im
q
]
T
. Finally, we define for the whole
system Q = [Q
T
1
,...,Q
T
n
a
]
T
and
˙
Q = [
˙
Q
T
1
,...,
˙
Q
T
n
a
]
T
.
The cameras mounted on the end effectors are
modeled using the pinhole model. Thus, the pro-
jection matrices H
I
i
/c
i
mapping the 3D coordinates
(x,y,z) of a point in the camera frame F
c
i
to its 2D
projection (X,Y ) on the image plan F
I
i
is defined as
follows:
X
Y
z
1
=
f /z 0 0 0
0 f /z 0 0
0 0 1 0
0 0 0 1
x
y
z
1
(1)
In this work, the arms are controlled to make each
camera reach a pose defined by the coordinates of
point visual features in the image space. To do so, one
uses n
a
landmarks made of four points. When consid-
ering the i
th
camera/target couple, the coordinates of
the projection of each point on the image is denoted
S
il
= [X
il
,Y
il
]
T
, with i ∈ [1,...,n
a
] and l ∈ [1, 2,3,4].
Thus, the visual feature vector for each camera is de-
fined as S
i
= [S
i1
,S
i2
,S
i3
,S
i4
]
T
, whereas the system
one is given by S = [S
T
1
,...,S
T
n
a
]
T
. In the same way,
a vector for the visual feature desired coordinates of
each camera is defined as S
∗
i
= [S
∗
i1
,S
∗
i2
,S
∗
i3
,S
∗
i4
]
T
.
Visual Predictive Control of Robotic Arms with Overlapping Workspace
131

2.2 Prediction Models
A visual predictive control scheme requires to be able
to predict the values of the visual features for a given
sequence of control inputs. In (Allibert et al., 2010),
the authors present two ways to perform the predic-
tion step for a flying camera: the local and global ap-
proaches. This section is devoted to the presentation
of both methods for the case of a 6 degrees of freedom
camera embedded on a robotic arm.
2.2.1 The Global Model
The global approach is based on the robot geomet-
ric model and the camera projection matrix. The idea
consists of computing the 3D coordinates of the fea-
tures in the next camera frame, then to project them
onto the camera image plan. To do so, let us con-
sider a discrete time system with a sampling period
T
s
, where t
k+1
= t
k
+ T
s
, and the notation .(k) = .(t
k
).
The configuration Q
i
(k + 1) of the i
th
arm, with i ∈
[1,...,n
a
], at the next iteration obtained after applying
the control inputs
˙
Q
i
(k) is given by:
Q
i
(k +1) = Q
i
(k) +
˙
Q
i
(k)T
s
(2)
Knowing the arm configuration at instants t
k
and t
k+1
,
it is then possible to compute the homogeneous trans-
formation matrices between the camera frame F
c
i
and
the base one F
b
.
¯o
F
b
(.) = H
b/c
i
(.) ¯o
F
c
i
(.) (3)
where ¯o are the homogeneous coordinates of a point
feature expressed in the base or camera frame. Fi-
nally, coupling (3) with (1), one obtains a predic-
tion of the coordinates of a point feature in the image
space.
S
il
(k +1) =
H
I
i
/c
i
(k +1)H
−1
b/c
i
(k +1)H
b/c
i
(k)H
−1
I
i
/c
i
(k)S
il
(k)
(4)
2.2.2 The Local Model
The local approach relies on the differential equation
mapping the derivative of the visual feature coordi-
nates
˙
S
il
to the robot control input vector
˙
Q
i
. To ob-
tain this equation, one uses the robot’s Jacobian J
i
,
mapping the camera kinematic screw T
c
i
and
˙
Q
i
(5),
and the interaction matrix L
il
, mapping
˙
S
il
to T
c
i
(6).
T
c
i
= J
i
˙
Q
i
(5)
˙
S
il
= L
il
T
c
i
(6)
where
L
il
=
"
−
1
z
l
0
X
l
z
l
X
l
Y
l
−(1 + X
2
l
) Y
l
0 −
1
z
l
Y
l
z
l
1 +Y
2
l
−X
l
Y
l
X
l
#
(7)
By combining equations (5) and (6), one obtains the
following local model for each arm/camera couple:
˙
S
il
= L
il
J
i
˙
Q
i
(8)
2.2.3 Usability of the Models
When considering using one of the models on an ex-
perimental system, several aspects have to be taken
into account. First, both models require a mea-
sure/estimate of the visual feature depth z (see equa-
tions (1) and (7)). However, when using a monocular
camera, this value can only be retrieved by estimation.
Another widely adopted option, consists of using a
constant value, such as the depth value at the initial
or desired pose (Chaumette and Hutchinson, 2006).
The second issue is related to the integration of the
local model to obtain the prediction equation. A first
option consists of using an advanced numeric scheme
to accurately compute the integration, whereas a sec-
ond one relies on a linear approximation of the model,
such as:
S
il
(k +1) = S
il
(k) +L
il
J
i
˙
Q
i
(k)T
s
(9)
Thus, depending on the user choices regarding these
issues, the prediction feature coordinates will be more
or less accurate. In section 4, different configurations
will be evaluated for our specific application in order
to select the most appropriate and realistic solution.
3 CONTROLLER DESIGN
In this section the control of the arms motion to reach
their own targets and compounding necessary con-
straints are presented. To achieve these goals, NMPC
control has been implemented to find the optimal in-
puts vector which minimizes a cost function subjects
to constraints. To do so, we first present the cost func-
tion to be minimized in order to reach the desired tar-
gets. Then, the expression of each constraint will be
defined.
3.1 Visual Predictive Control
The proposed VPC scheme couples NMPC (Nonlin-
ear Model Predictive Control) with IBVS (Image-
Based Visual Servoing). Thus, similarly to NMPC,
it consists of computing an optimal control sequence
¯
˙
Q(.) that minimizes a cost function J
N
P
over a pre-
diction horizon of N
P
steps while taking into account
a set of user-defined constraints C(
¯
˙
Q(.)). Moreover,
similarly to IBVS, the task to achieve is defined as an
error in the image space. Thus, the cost function to
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
132

minimize is the sum of the quadratic error between
the visual feature coordinates
ˆ
S(.) predicted over the
horizon N
p
and the desired ones S
∗
. It then possible
to write the VPC problem as:
¯
˙
Q(.) = min
˙
Q(.)
J
N
P
(S(k),
˙
Q(.))
(10)
with
J
N
P
(S(k),
˙
Q(.)) =
k+N
p
−1
∑
p=k+1
[
ˆ
S(p) − S
∗
]
T
[
ˆ
S(p) − S
∗
]
(11)
subject to
ˆ
S(.) = (4) or (8) (12a)
ˆ
S(k) = S(k) (12b)
C(
¯
˙
Q(.)) ≤ 0 (12c)
As mentioned in the previous section, the visual fea-
ture coordinates can be predicted either using the
global or local models (equation (12a)). To compute
the prediction, one uses the last measured visual fea-
tures (equation (12b)). Finally, equation (12c) defines
the set of constraints to be taken into account when
minimizing the cost function (11).
Thus, solving equation (10) leads to the optimal
sequence of control inputs
¯
˙
Q(.). In this work, and
as it is usually done, only the first element
¯
˙
Q(1) of
the sequence is applied to the system. At the next
iteration, the minimization problem is restarted, and a
new sequence of optimal control inputs is computed.
This loop is repeated until the task is achieved, e.i.,
the cost function (11) is vanished.
3.2 Constraints
As seen in the previous section, it is possible to add a
set of constraints in the minimization problem. In this
section, one presents the constraints related to the ge-
ometry of the robot, the velocity of the joints, and the
field of view of the camera. One finishes with defining
a set of constraints that guarantee the non-collision of
the arms despite sharing a common workspace.
3.2.1 System Constraints
The joint velocity lower and upper bounds are respec-
tively denoted
˙
Q
min
and
˙
Q
max
. They are two N
˙
Q
long
vector, with N
˙
Q
= n
a
m
q
N
p
. They allow to define the
lower and upper limit of each joint of each arm over
the prediction horizon. Consequently, the constraint
on
˙
Q(.) is described in the domain κ = [
˙
Q
min
,
˙
Q
max
],
and the velocity constraint is then written as:
˙
Q −
˙
Q
max
˙
Q
min
−
˙
Q
≤ 0 (13)
Mechanical limits follow the same principle. The
lower and upper bounds of the angular values are de-
noted Q
min
and Q
max
. They are two N
Q
long vector,
with N
Q
= n
a
m
q
N
p
. These constraints are then given
by:
Q − Q
max
Q
min
− Q
≤ 0 (14)
Finally, the visual constraints are defined by the
image dimension. Ones denotes the bounds by S
min
and S
max
. They are two N
S
long vector, with N
S
=
8n
a
N
p
. Thus, all the predicted visual features coor-
dinates need to be kept into this space, and the con-
straints can then be written as:
S − S
max
S
min
− S
≤ 0 (15)
3.2.2 Overlapping Workspace Constraint
Due to the overlapping workspace, it is mandatory
to guarantee the non-collision between the arms. To
do so, one computes the shortest distance d
i, j|i
0
, j
0
be-
tween the j
th
joint of the i
th
arm and the j
0th
joint of
the i
0th
arm. The closest distance is evaluated as the
norm of the segment perpendicular to both assessed
links as it is illustrated in figure 1. Finally, in order to
avoid collision, one defines the following constraint:
d
min
− d
≤ 0 (16)
where d = [d
1,1|2,1
,...,d
n
a
−1,m
q
|n
a
,m
q
] and d
min
is a pre-
defined distance.
Figure 1: Computation of the shortest distance d
i, j|i
0
, j
0
be-
tween links L
i j
and L
i
0
j
0
.
3.2.3 Terminal Constraint
To make the system converge, it is mandatory to guar-
antee that the predictive control problem is feasible
(Lars and Pannek, 2016). To check the feasability, one
adds a final constraint in the optimization problem. It
is defined as the error between the prediction of the vi-
sual feature coordinates
ˆ
S(k + N
p
− 1) obtained at the
Visual Predictive Control of Robotic Arms with Overlapping Workspace
133

end of the prediction horizon, and the desired ones S
∗
.
If the solver cannot compute a sequence of control in-
puts
¯
˙
Q that respects this constraint, then the problem
is not feasible, and there is no guarantee regarding the
system convergence.
ˆ
S(k + N
p
− 1) − S
∗
≤ 0 (17)
All the constraints are now defined and can be in-
tegrated into the non-linear function C(
¯
˙
Q(.)):
C(
¯
˙
Q) ≤ 0 ⇒
˙
Q −
˙
Q
max
˙
Q
min
−
˙
Q
Q − Q
max
Q
min
− Q
S − S
max
S
min
− S
ˆ
D
min
− D
ˆ
S(k + N
p
− 1) − S
∗
≤ 0 (18)
Thus, the optimal input must belong to the domain
defined by C(
¯
˙
Q(.)).
4 SIMULATION
In this section, one presents the results obtained by
simulating the control of two arms with MATLAB
software. A 7 DOF model has been selected, based on
the arms embedded on the PR2 robot. In these simu-
lations the task consists of positioning the cameras at-
tached to each end-effector with respect to two given
targets. Each desired position is defined in the image
space by S
i
= [x
1
,y
1
,x
2
,y
2
,x
3
,y
3
,x
4
,y
4
], which are
the coordinates of four points representing the corre-
sponding target. Moreover, the prediction horizon is
set up at N
p
= 5. Regarding the constraints, the an-
gular velocity limits for the first prediction step are
given by κ = [−0.2 0.2] for each joint, whereas it
is extended to κ = [−5 5] for the rest of the predic-
tion step. This allows to decrease the computation
while guaranteeing a feasible control input for the
first step. The size of the image is S
min
= [−4 − 4]
and S
max
= [4 4]. The angular constraints on each
joint are setup as described in the PR2 documenta-
tion (Garage, 2012). Finally the minimum collision
avoidance distance is fixed to D
min
= 0.1. The ini-
tial coordinate of the visual features are computed
based on the initial configuration of the robot given
by q
init
= [0
π
2
0 0 0 0 0 0
π
2
0 0 0 0 0]
T
for every
simulation. Finally, one fixes T
s
= 50ms.
4.1 Comparison between Different
Prediction Methods
The first set of simulation assesses the accuracy of
different predictive models presented in section 2.2.
To do so, one drives the arms from q
init
to q
∗
=
[−
π
8
π
2
0 0 0 0 0 0
π
2
0 0 0 0 0]
T
. During this motion,
the coordinates of the visual features predicted over
the prediction horizon, are compared with a ground
truth. In this case, it consists of the prediction ob-
tained with the global model computed with the real
depth of each visual feature.
Figure 2 shows the evolution over the simulation
of the quadratic error between the predicted coordi-
nates of one visual feature and the ground truth. Six
models are compared by combining the global model
(solid lines), local Euler approximation (dashed lines)
and local Runge Kutta approximation (dotted lines)
with the depth values real z (black) and desired z
∗
(blue). It can be seen that the global models and
the local Runge Kutta are significantly more accu-
rate than the local Euler one. Indeed, using this latter
prediction scheme introduces a large error, and might
not allow the system to converge toward the desired
configuration. In a second figure 3, the previous er-
rors were summed over the simulation to offer a bet-
ter view of model performances. When considering
the use of the real depth, the global model is the most
accurate. However, this result is obtained in a sim-
ulation, and its use in a real context would require
an estimator of the depth. Thus, one now considers
one more realistic case where the depth is approxi-
mated with the constant value z
∗
. In this case, the
local Runge Kutta is the most accurate model. Thus,
for the rest of the simulations the local Runge Kutta
model with z
∗
is used to evaluate the performances in
a more realistic scenario.
Figure 2: Quadratic errors of prediction over the simulation
-Solid: Global model -Dashed: Local Euler -Dotted: Local
Runge Kutta -Black: Real z -Blue: Desired z.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
134
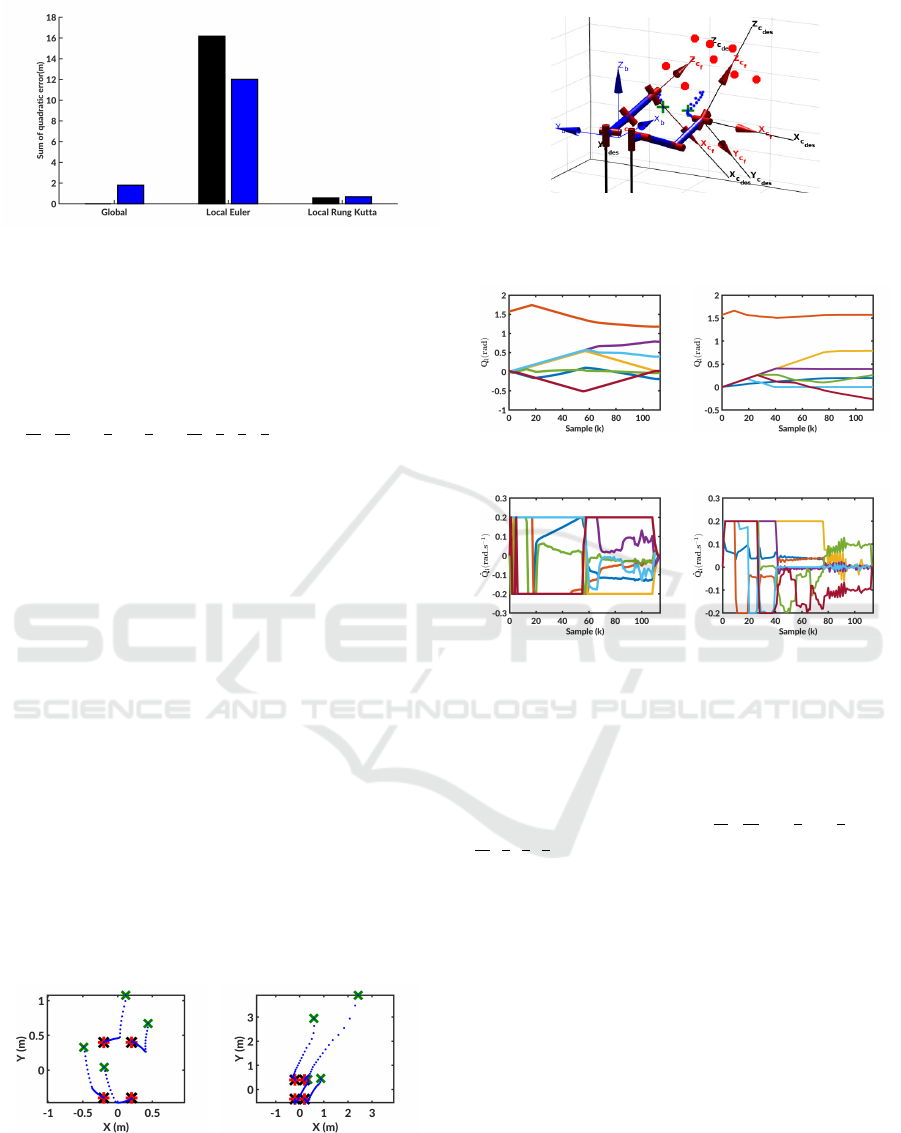
Figure 3: Sum of the quadratic errors of prediction for
global, local Euler and local Runge-Kutta methods -Black:
Real z -Blue: Desired z.
4.2 First Validation
For the second simulation, the system has
to reach the desired configuration q
∗
=
[−
π
16
3π
8
0
π
4
0
π
8
0
π
16
π
2
π
4
π
8
0 0 0]
T
from the
initial one q
init
while dealing with the previously
presented constraints. This visual predictive control
was performed using the local model with Runge
Kutta approximation and the desired depth z
∗
. The
trajectories in the images of visual features are
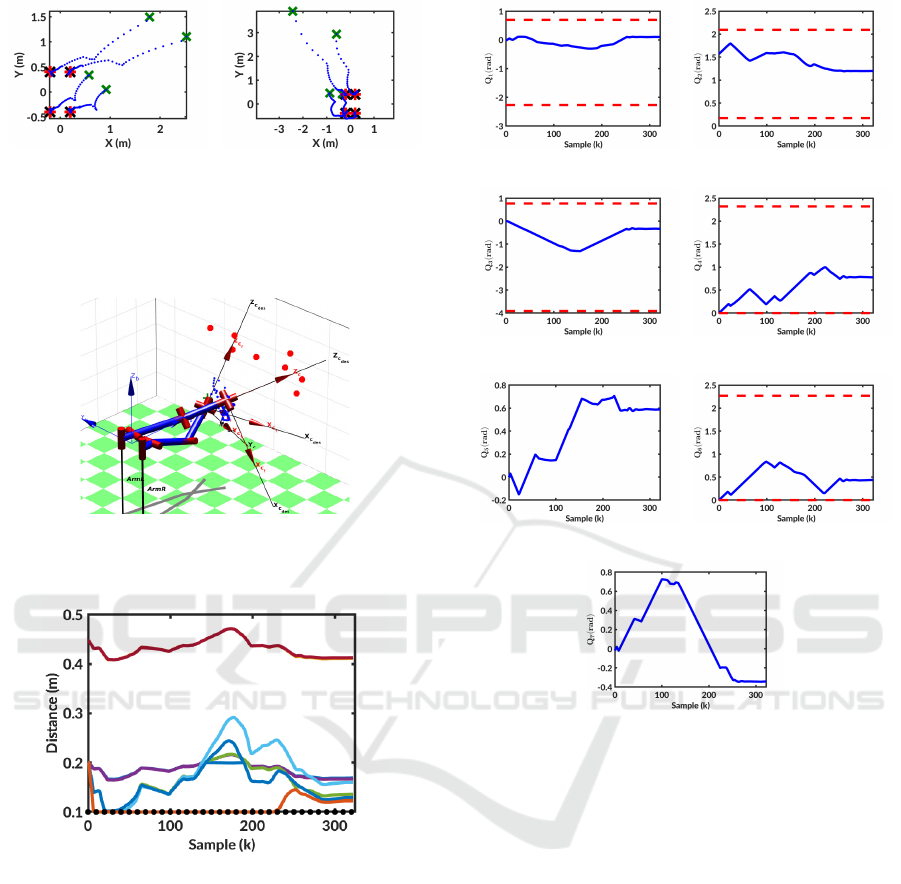
displayed in figure 4 and show the achievement of
the task for both cameras. Indeed, the proposed
controller was able to drive both arms to make the
cameras converge towards the desired features from
the initial ones (respectively represented by the
red and green crosses in figures 4(a) and 4(b)). To
achieve the task in the image space, the arms had
to reach the poses presented in figure 5. During the
realization of this task, the image limits were never
reached. Similarly there was no risk of collision
during the servoing. Moreover, it can be seen in
figures 6(a) and 6(b) that the constraints on the joint
configurations were taken into account. Similarly, in
figures 6(c) and 6(d), one can see that the constraints
on the joint velocities were taken into account to
achieve the task. Indeed, the applied commands stay
within the given range κ = [−0.2 0.2] all along the
simulation.
(a) Left camera - Local
model
(b) Right camera - Local
model
Figure 4: Visual features location using local Runge-Kutta
model and real z - Blue dotted: Trajectories - Red crosses:
Final locations - Green crosses: Initial locations.
Figure 5: Final poses of the arms - Red dots represent the
two targets - Green crosses are the initial poses of the end
effectors.
(a) Right arm joints angular
values
(b) Left arm joints angular
values
(c) Right arm joints angular
velocities
(d) Left arm joints angular
velocities
Figure 6: Joint configurations and velocities.
4.3 Collision Avoidance
In this last simulation, the system has to reach the
desired configuration q
∗
= [
π
16
3π
8
0
π
4
0
π
8
0 −
π
16
π
2
π
4
π
8
0 0 0]
T
. This set is run using the Runge
Kutta local model with the desired depth values. One
more time the desired visual features are reached from
the initial poses (figure 7). However, as it can be seen
in figure 8, the arms had to cross each other to reach
the desired poses. Thanks to the shared environment
constraint included in the control problem, the colli-
sion was avoided. Indeed, figure 9 shows that the dis-
tance between the different links was never smaller
than the fixed value D
min
= 0.1. In addition, the con-
straints on the joints angular values are respected. In
figure 10, it can be seen that the right arm joints never
reach their angular limits represented by red dashed
lines (the joints represented in figures 10(e) and 10(g)
do not have limits on PR2 robot). Similarly, the con-
trol inputs of the right arm present saturations due to
the angular velocity constraints, represented by red
dashed lines in figure 11, but never goes beyond.
Visual Predictive Control of Robotic Arms with Overlapping Workspace
135
(a) Visual features in image
left
(b) Visual features in image
right
Figure 7: Visual features location using local Runge-Kutta
model and real z - Blue dotted: Trajectories - Red crosses:
Final locations - Green crosses: Initial locations.
Figure 8: Final poses of the arms - Red dots represent the
two targets - Green crosses are the initial poses of the end
effectors.
Figure 9: Collision distance d - Solid: Distances between
links, Dotted: Minimal allowed distance.
5 CONCLUSION
In this paper, we have addressed the problem of fruit
picking in orchards performed by a multi-arms robot.
The goal is to bring the different end-effectors close
to their designated fruits while taking into account the
dynamic environment as well as the constraints in-
herent to the system mechanics, the visual manipu-
lation and the shared workspace. The proposed solu-
tion relies on a VPC strategy to fulfill these require-
ments. First, several prediction models were pre-
sented. Next, the visual servoing task and the con-
straints were described including them in a NMPC
(a) q
11
joint angular values (b) q
12
joint angular values
(c) q
13
joint angular values (d) q
14
joint angular values
(e) q
15
joint angular values (f) q
16
joint angular values
(g) q
17
joint angular values
Figure 10: Configuration of the right arm over the simu-
lation - Blue solid: Angular joint value q
1 j
- Red dashed:
Maximum angles.
strategy. Finally, simulations based on PR2 manip-
ulators were performed to assess the performance of
each predictive model and to validate the completion
of the servoing. The obtained results show the effi-
ciency of this approach to perform various tasks in a
shared workspace. However, multiple steps still need
to be accomplished. First, this method must be inte-
grated on a real robot. This step will require to opti-
mize the computational time to run it in real time. In
addition, a constraint avoiding the target occlusions
in the image must be integrated. Finally, this manip-
ulation controller will be coupled with our previous
works about the autonomous navigation in orchards
to perform a complete fruits picking task.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
136
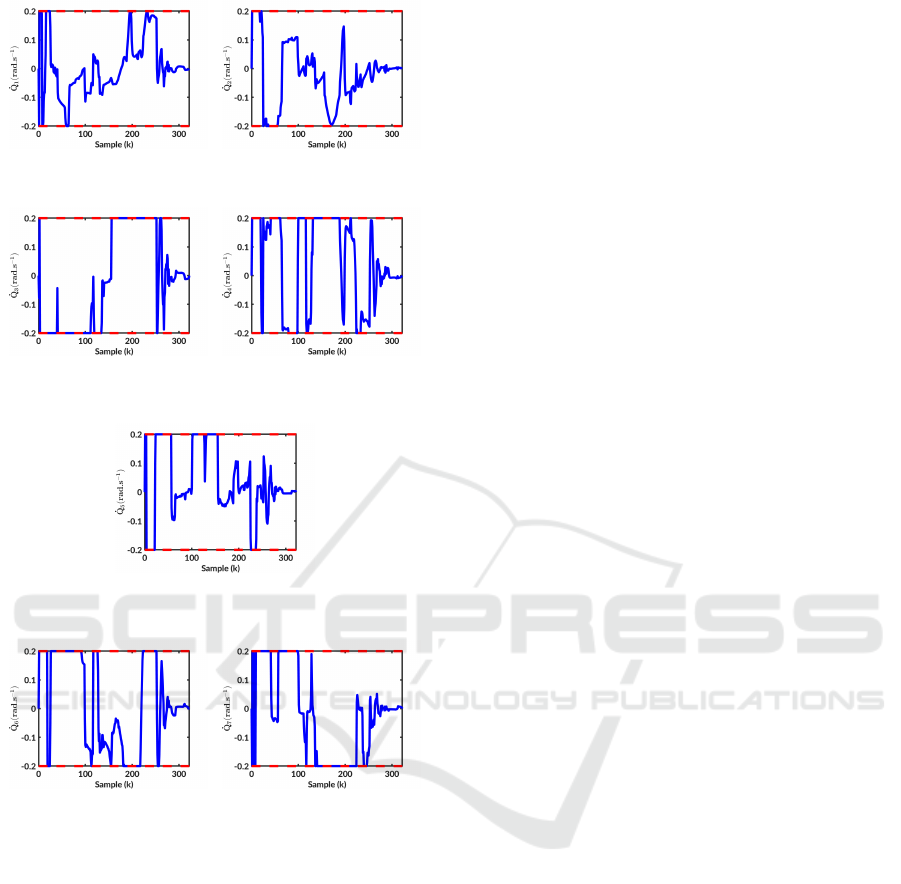
(a) ˙q
11
joints angular veloc-
ity
(b) ˙q
12
joints angular veloc-
ity
(c) ˙q
13
joints angular veloc-
ity
(d) ˙q
14
joints angular veloc-
ity
(e) ˙q
15
joints angular veloc-
ity
(f) ˙q
16
joints angular veloc-
ity
(g) ˙q
17
joints angular veloc-
ity
Figure 11: Right arm joints velocities - Blue solid: Joint
velocity value - Red dashed: Maximum velocities.
REFERENCES
Allibert, G., Courtial, E., and Chaumette, F. (2010). Pre-
dictive Control for Constrained Image-Based Visual
Servoing. IEEE Transactions on Robotics, 26(5):933–
939.
Chaumette, F. and Hutchinson, S. (2006). Visual servo con-
trol. i. basic approaches. IEEE Robotics & Automation
Magazine, 13(4):82–90.
Diehl, M. and Mombaur, K., editors (2006). Fast motions
in biomechanics and robotics: optimization and feed-
back control. Number 340 in Lecture notes in con-
trol and information sciences. Springer, Berlin ; New
York. OCLC: ocm71814232.
Durand-Petiteville, A., Le Flecher, E., Cadenat, V., Sen-
tenac, T., and Vougioukas, S. (2017). Design of a
sensor-based controller performing u-turn to navigate
in orchards. In Proc. Int. Conf. Inform. Control, Au-
tomat. Robot., volume 2, pages 172–181.
Foley, J. A., Ramankutty, N., Brauman, K. A., Cassidy,
E. S., Gerber, J. S., Johnston, M., Mueller, N. D.,
O’Connell, C., Ray, D. K., West, P. C., Balzer, C.,
Bennett, E. M., Carpenter, S. R., Hill, J., Monfreda,
C., Polasky, S., Rockstr
¨
om, J., Sheehan, J., Siebert,
S., Tilman, D., and Zaks, D. P. M. (2011). Solutions
for a cultivated planet. Nature, 478:337–342.
Garage, W. (2012). Pr2 user manual.
Grift, T., Zhang, Q., Kondo, N., and Ting, K. C. (2008). A
review of automation and robotics for the bio- indus-
try. Journal of Biomechatronics Engineering, 1(1):19.
Hajiloo, A., Keshmiri, M., Xie, W.-F., and Wang, T.-T.
(2015). Robust On-Line Model Predictive Control for
a Constrained Image Based Visual Servoing. IEEE
Transactions on Industrial Electronics, pages 1–1.
Lars, G. and Pannek, J. (2016). Nonlinear model predictive
control. Springer Berlin Heidelberg, New York, NY.
Le Flecher, E., Durand-Petiteville, A., Cadenat, V., Sen-
tenac, T., and Vougioukas, S. (2017). Implementa-
tion on a harvesting robot of a sensor-based controller
performing a u-turn. In 2017 IEEE International
Workshop of Electronics, Control, Measurement, Sig-
nals and their Application to Mechatronics (ECMSM),
pages 1–6. IEEE.
Sauvee, M., Poignet, P., Dombre, E., and Courtial, E.
(2006). Image Based Visual Servoing through Non-
linear Model Predictive Control. In Proceedings of
the 45th IEEE Conference on Decision and Control,
pages 1776–1781, San Diego, CA, USA. IEEE.
Van Henten, E., Hemming, J., Van Tuijl, B., Kornet, J., and
Bontsema, J. (2003). Collision-free Motion Planning
for a Cucumber Picking Robot. Biosystems Engineer-
ing, 86(2):135–144.
Vougioukas, S. G., Arikapudi, R., and Munic, J.
(2016). A Study of Fruit Reachability in Orchard
Trees by Linear-Only Motion. IFAC-PapersOnLine,
49(16):277–280.
Zhao, Y., Gong, L., Huang, Y., and Liu, C. (2016a). A
review of key techniques of vision-based control for
harvesting robot. Computers and Electronics in Agri-
culture, 127:311–323.
Zhao, Y., Gong, L., Liu, C., and Huang, Y. (2016b). Dual-
arm Robot Design and Testing for Harvesting Tomato
in Greenhouse. IFAC-PapersOnLine, 49(16):161–
165.
Visual Predictive Control of Robotic Arms with Overlapping Workspace
137
