Low-cost Sonar based on the Echolocation

Thiago Moreira

1 a

, Jos

e Lima

2,3 b

, Paulo Costa

3 c

and M

arcio Cunha

1 d

Academic Department of Electronic, Federal University of Technology, Paran

a, Brazil

CeDRI - Research Centre in Digitalization and Intelligent Robotics, Polytechnic Institute of Braganc¸a, Braganc¸a, Portugal

INESC TEC - INESC Technology and Science and Faculty of Engineering of University of Porto, Porto, Portugal

Keywords: Object Detection, Echolocation, Sonar, Mobile Robot Navigation.

Abstract:

In the world of mobile robot navigation, the ultrasonic sensors stand out for presenting attractive features at

an affordable cost. The main problem in the use of these devices lies in the difﬁculty of correctly interpreting

the obtained data, which means that their efﬁciency is limited. This paper focuses on the improvement and

implementation of a low cost location system based on ultrasonic sensors. Through the combination of math-

ematical techniques and signal processing it is possible to make the system more accurate and reliable. The

developed system includes the data acquisition, the signal ﬁltering, and the trigonometric methods to estimate

the coordinates of a target and can be assembled in a mobile robot.

1 INTRODUCTION

One of the great challenges of mobile robot naviga-

tion is the detection of targets and their location. Most

systems used to solve this task are vision based and

sensor (non-vision) based. In the ﬁrst one, detec-

tion through cameras and image processing are sub-

ject to a lack of precision, which can arise as a result

of variation in environmental conditions like dark-

ness, foggy or low visibility (Patkar and Tasgaonkar,

2016). Moreover, the computational consumption and

the price of these systems are still high (Kreczmer,

2010).

The cost-effective of robots is an important fea-

ture to consider before the building process. To keep

their cost down, expensive sensors and devices should

be evaluated. In this way, ultrasonic sensor seems to

be suitable to deal with this problem (Wu and Tsai,

2001; Kim and Choi, 2008). It has proven to be very

efﬁcient, economical and accurate (Lim et al., 2014).

Systems based on ultrasonic sensor have many

advantages over other methods. For example, in

applications that require reduced size the modules

can be very small without interfering in their perfor-

mance. In addition, it is capable of operating in sev-

https://orcid.org/0000-0002-6132-2914

https://orcid.org/0000-0001-7902-1207

https://orcid.org/0000-0002-4846-271X

https://orcid.org/0000-0001-7506-4488

eral environments in which other devices can not be

used (Kim and Choi, 2008).

In robotic applications, ultrasonic sensing is rarely

used beyond simple functions such as obstacles avoid-

ance. However, some works show just how useful

the sensor can be (Schillebeeckx et al., 2011; Popelka

et al., 2016). The best known example that use ul-

trasonic navigation are the bats. They’re able to

avoid obstacles even at high speeds when ﬂying in the

dark (Cheeke, 2016). The main difference between

an ultrasonic range ﬁnder and the bat is that it has two

ears, which allows them to detect which direction the

echo comes from (Kreczmer, 2010).

The major drawback of this technique occurs due

to the wide beam of an emitted signal, causing a mis-

interpretation of the object’s real reﬂection. When

irregularities of the object surface are much smaller

than the wavelength of the signal, there is also the

called multiple reﬂection effect. The last event can

be noticed when successive measurements are per-

formed in a regular short time. In an attempt to avoid

this problem, a system containing two receivers and a

transmitter is required (Kreczmer, 2010).

Inspired by the echo location of the animals, this

paper proposes a low cost ultrasonic binaural system

based on accuracy techniques and discusses the difﬁ-

culties associated with the use of ultrasonic measure-

ments in indoor environments.

In section 2, the main distance estimation methods

are brieﬂy described. In section 3, a review is made

818

Moreira, T., Lima, J., Costa, P. and Cunha, M.

Low-cost Sonar based on the Echolocation.

DOI: 10.5220/0008119108180825

In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 818-825

ISBN: 978-989-758-380-3

about the conventional ultrasonic range system and

the binaural sensor system. In section 4, the architec-

ture of the proposed system is presented. In section 5,

the method of triangulation using ultrasonic sensors is

introduced. In section 6, the results of the experimen-

tal tests are reported. Finally, in section 7 the results

are discussed and conclusions drawn.

2 DISTANCE ESTIMATION

METHODS

The main approaches to determine the distance

through ultrasonic waves are given by the phase shift

and time-of-ﬂight (TOF). The ﬁrst strategy comprises

the continuous calculation of the phase shift between

the transmitted and received signal. However, this

strategy has a very narrow measurable range. The sec-

ond strategy, unlike the ﬁrst one, allows to measure

greater distances and consists in determining the time

that a wave takes to reach the receiver. The transmit-

ter sends the sound waves to an object or obstacle and,

when it is detected, returns to the receiver (Huang and

Huang, 2009; Queir

os et al., 2006).

There are several methods for estimating the TOF,

in the following subsections the most common tech-

niques are presented.

2.1 Threshold Detection

This form is the simplest and fastest way to calcu-

late the TOF. It involves transmitting and detecting

the arrival of an ultrasonic wave when the received

signal exceeds, for the ﬁrst time, a predeﬁned thresh-

old level, as seen in Figure 1. There are some bene-

ﬁts to using this method, it requires no complex com-

putation and can be performed with simple circuitry.

The main problem of this method is that it typically

estimates a higher TOF compared to the actual one.

This happens due to the long rise time of the signal,

added to other factors, such as low signal-to-noise

ratio (SNR) and inherent bias (Jackson et al., 2013;

Queir

os et al., 2006).

As noise increases the likelihood of incorrect

readings also increases, and systems that use thresh-

old as a reference value are vulnerable to this type

of error. In low SNR conditions, it is recommended

to amplify the signal, or equivalently, adjust the de-

tection threshold in order to reduce the system uncer-

tainty. According to (Jackson et al., 2013), the inher-

ent bias occurs for two reasons: the ﬁrst is that no

matter how good the transducer performance is, there

will always be a rise time when a signal is detected;

Figure 1: Threshold detection method (Kuc and Siegel,

1987).

the second and most crucial is the threshold level set-

ting, this is a critical factor for the bias, because if a

low threshold is set the occurrence of false positives

tends to increase.

2.2 Cross-correlation

The TOF estimation can be considered as a time de-

lay issue, for instance, suppose an ultrasonic signal

(t) is generated, so when it propagates in the air

and is reﬂected, the time between the transmission

and the reception of the signal is given by a delay τ.

Thus, techniques for calculate the time delay should

be used. Among them, cross-correlation has been

highlighted (Marioli et al., 1992). Cross-correlation

is a quantitative operation in the time domain to re-

late two signals, when applied between the transmit-

ted and received signal, the result is a peak at the time

delay t

, as shown in Figure 2. The cross-correlation

c(t) is calculated by:

c(t) =

+∞

−∞

(t)s

(t + τ)d(τ) (1)

where s

(t) is the transmitted signal, s

(t + τ) is

the signal received and shifted in time.

Figure 2: Cross-correlation method. Adapted from (Jack-

son et al., 2013).

Low-cost Sonar based on the Echolocation

819

The main disadvantage is that it requires a high

computational consumption, and second (Xu et al.,

2009) this method is only suitable for slightly disper-

sive waves, otherwise the method is not so efﬁcient.

2.3 Envelope Detection

Envelope detection is an alternative to the other meth-

ods mentioned above, which can be assumed as an

intermediary version between threshold detection and

cross-correlation. In (Xu et al., 2009) a comparison

made from the most commom procedures of TOF

estimation demonstrated that envelope detection ob-

tained satisfactory results, only losing to the cross cor-

relation. However, in terms of computational process-

ing this technique is most convenient.

The envelope detector makes use of the Hilbert

Transform to generate an analytical signal, whose ab-

solute value represents the envelope of the measured

signal. The analytical signal y(t) of a real signal x(t)

is deﬁned by:

y(t) = x(t) + j h(t) (2)

where h(t) is the Hilbert Transform of x(t) and j =

√

−1. The magnitude of the analytic signal, which

is identical to the real signal, is called envelope as

seen in Figure 3. Thus, from the envelope extraction

it is possible to locate the peaks and determine the

time between sending and receiving the echo signal.

Hence, the problem of setting the threshold level is

eliminated.

Figure 3: The envelope extraction of the echo signal.

3 SENSOR SYSTEM

In the present work the binaural sensor system was

adopted to improve the system perfomance, but be-

fore studying how it works in the following subsec-

tions a brief analysis of the traditional use of the ul-

trasonic sensor is presented in order to clarify the dif-

ference between these two types.

3.1 Conventional Ultrasonic Ranging

System

This scheme is basically a conventional TOF sys-

tem. The standard mode of operation is to transmit

an acoustic signal through the air and measure the du-

ration until it is reﬂected by some object. The distance

d can be obtained from

d =

c ·T

(3)

where c is the sound velocity and T

is the

TOF (Kuc and Siegel, 1987).

As previously mentioned, the beam width of these

sensors is large, which makes it unfeasible to lo-

cate the object using just one sensor. Furthermore,

only the ﬁrst reﬂection is measured in this conﬁgura-

tion, making the amount of information obtained ex-

tremely limited (Peremans et al., 1993).

Figure 4: The beam width of a single sensor. Adapted

from (Peremans et al., 1993).

3.2 The Binaural Sensor System

The binaural sensor arrangement, presented in Fig-

ure 5, aims to combine the use of two ultrasonic

sensors to provide more detailed spatial information

and map the environment. Conforming to (Kreczmer,

2010) the disadvantages of a single sensor are reduced

when a multi-sonar system is used. The proposed sys-

tem consists in three conventional ultrasonic sensors,

one of which acts as a transmitter and the other two

as a receiver. In this work it is assumed that the prop-

agation of sound waves occurs in a horizontal plane,

equivalent to the two-dimensional space. Thus, the

location of an object is deﬁned by the region of inter-

section with the horizontal plane through the sensors

A and B, called detection area, as shown in Figure 6.

The receivers, sensors A and B, are separated by

a known baseline (l) that allows locating the detected

objects in a planar environment, estimating the TOF

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

820

Figure 5: The Binaural sensor arrangement.

between the object and each sensor through the en-

velope detection. Then, the distance calculation is

solved by trigonometric techniques. Fixing the angle

and baseline it is also possible to change the detection

ﬁeld when the two ultrasonic beam patterns overlap.

The ideal positioning of the system was deﬁned

by the baseline and the α angle, as can be seen in Fig-

ure 6. The maximum width of the detection area oc-

curs when the beam patterns overlap completely, that

is, with a close distance and α = 90

◦

. When the width

is small, as in Figure 7b, the behavior is similar to sys-

tem mentioned in Subsection 3.1. When the width is

larger, as shown in Figure 7a, it is possible to expand

the coverage area. By adjusting the angle of rotation

the points of intersection can increase or decrease, and

the mapping of all valid positions for the detection can

be made by tracing arcs with ﬁxed distances in the lo-

cating cone.

Figure 6: Detection area formed by the beam patterns.

Adapted from (Gearhart et al., 2009).

4 SYSTEM ARCHITECTURE

The system is composed by three low-cost ul-

trasonic sensors HY-SRF05 and a microcontroller

STM32F103C8T ARM Cortex-M3 with two built-in

analog to digital (A/D) converters. The ultrasonic

burst is performed by sensor C and the raw echo sig-

nal received by sensors A and B is sent to the 12

bits A/D converters of the microcontroller with a sam-

pling rate of 320 kHz. Assuming the sound velocity

as approximately 340 m/s, it can be stated that the dis-

tance is covered 0.034 cm/µs. The reciprocal is equal

to 29.412 µs/cm, and considering a round trip cor-

responds to 58.824 µs/cm. Using this constant it is

possible to simplify the determination of the distance

and substitute the Equation (3) by the equation below:

d =

, (4)

where K ≈ 59.

Four thousand readings are stored from each sen-

sor, which if multiplied by the sampling period,

T s = 3.125 µs, corresponds to a sample space of

12500 µs. Using the Equation (4) we can estimate that

the proposed system has a maximum range of about

212 cm depth, that is, along the y-axis. The x-axis is

bounded by the established baseline.

After the data acquisition, the samples are trans-

mitted over RS-232 protocol to the MATLAB, where

the envelope extraction and the TOF estimation of

sensors A and B are performed. Finally, the calcu-

lation of the object coordinates is executed. In order

to reduce the noise, a second-order Butterworth band-

pass ﬁlter was applied in the echo signal. The phase

delay produced by the ﬁlter was negligible. The sys-

tem overview is shown in Figure 8.

5 TRIANGULATION

Triangulation is the process of determining the lo-

cation of a target from known points using trigono-

metric techniques. Currently, triangulation is applied

(a) Wide overlap region.

(b) Thin overlap region.

Figure 7: Adapted from (Gearhart et al., 2009).

Low-cost Sonar based on the Echolocation

821

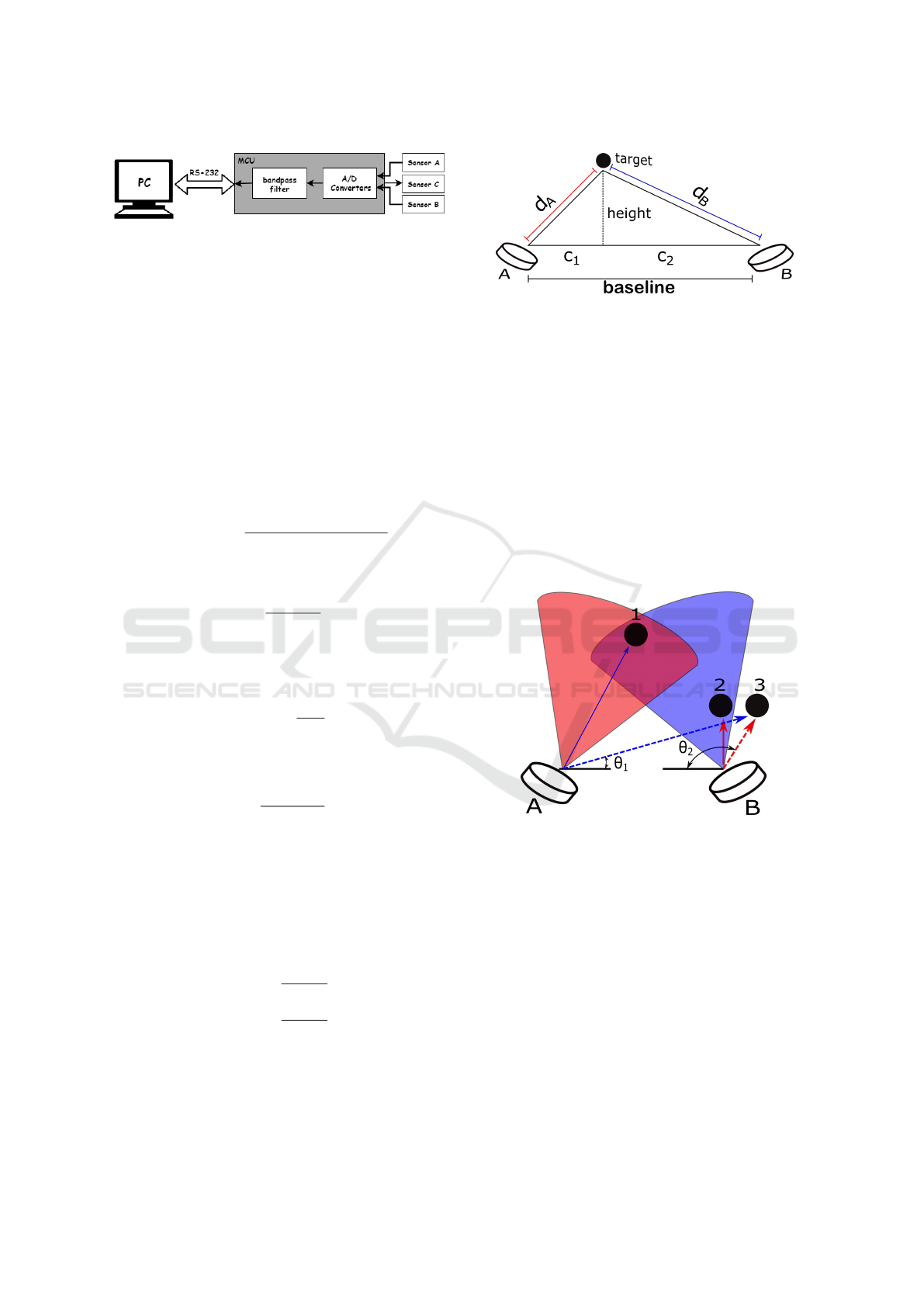
Figure 8: Hardware Implementation.

in several areas, including navigation, metrology and

astrometry. Generally, the number of sensors corre-

sponds to the number of dimensions of the estimated

position of the object, for example, two sensors can

indicate a location in 2D, while three in 3D (Gearhart

et al., 2009).

In geometry, there is a formula that allows to cal-

culate the area of any triangle when the lengths of the

three sides are known. This approach was discovered

by the mathematician Heron of Alexandria (B

enyi,

2003). Knowing the distance from the baseline be-

tween the sensors and the distance calculated by them,

it can be computed the area of the triangle formed us-

ing Heron’s formula, as shown in Equation 5:

∆(abc) =

p(p −a)(p −b)(p −c), (5)

p =

a + b +c

(6)

whose a,b,c are the known sides.

Alternatively, the area of a triangle is also given

by Equation 7:

∆(abc) =

b · h

(7)

where b is the base and h is the height of the triangle.

Rearranging the Equation (7), results in:

h =

∆(abc) · 2

(8)

If the area calculated in Equation 5 is replaced in

Equation 8 and the base by the known baseline, it is

possible to determine the y-coordinate of the object.

Figures 9 and 11 show the nomenclatures adopted for

the geometric parameters. The x coordinate can now

be calculated if the original triangle is separated into

two right triangles and after that the Pythagoras The-

orem is applied, according to the Equations 9 and 10:

−h

(9)

−h

(10)

where h, C

, C

, d

and d

can be seen in Figure 9.

If the Equation (9) is used, the system reference

for the coordinates on the x-axis will originate from

sensor A otherwise, from sensor B.

Figure 9: Typical triangulation.

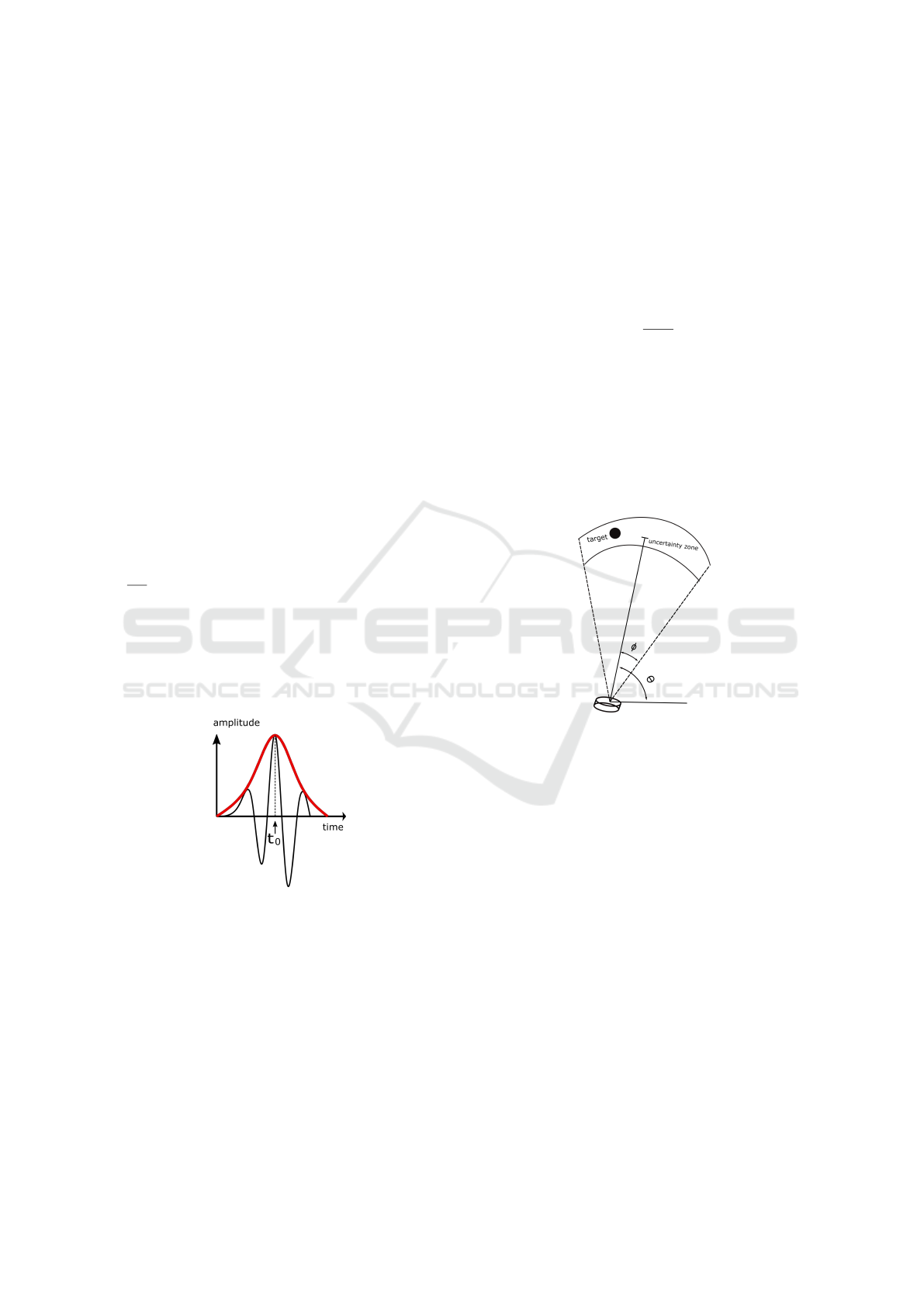
In Figure 4 it is possible to get a perspective of

the systems that use a single ultrasonic sensor. Ob-

jects can be detected anywhere into uncertainty zone.

However, without additional information the system

is not able to make a decision to avoid a collision,

only that there is an object present in the detection

ﬁeld.

Valid mathematical events but nonsense physical

can occur using the equations described previously,

such as when two objects are separate but are only

detected as one. Therefore, some constraints were de-

ﬁned in order to avoid incoherent data. To prevent the

error shown in Figure 10, it was observed that θ

and

angles are outside of the detection area.

Figure 10: Typical triangulation error. Adapted

from (Gearhart et al., 2009).

Figure 10 demonstrates that sensor A detects tar-

get 1 and sensor B detects target 2. However, θ

and

are outside the triangulation area, which causes a

misinterpretation resulting in a wrong coordinate (tar-

get 3).

The next equations and the proposed analysis

were also established by (Gearhart et al., 2009). Fig-

ure 11 demonstrates how θ

and θ

should be for a

valid detection region and evidence that θ

= α

±φ.

The α

is the angular position of the sensor n relative

to the x-axis. The φ is half the angle of the detection

beam, and is a value speciﬁc to each sensor model.

The angular limiting interval can be given by:

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

822

cos(α

−φ) ≤ cos θ

≤ cos(α

+ φ), which

cosθ

+ d

−d

2ld

(11)

Analogously to sensor B, the angular limiting range

is given by: cos(α

−φ) ≤ cos θ

≤ cos(α

+ φ), and

cosθ

+ d

−d

2ld

(12)

The α

, α

and φ are constant, so it is necessary to

calculate only cos θ

and cosθ

. Readings outside this

range are discarded.

Figure 11: Triangulation created from the sensors. Adapted

from (Gearhart et al., 2009).

6 RESULTS

The objective of the experimental tests was to analyze

the accuracy of the proposed method and the behavior

of the developed system. The tests were divided into

two situations: the ﬁrst with only one object and the

second with two objects. The following subsections

describe the procedures and results obtained.

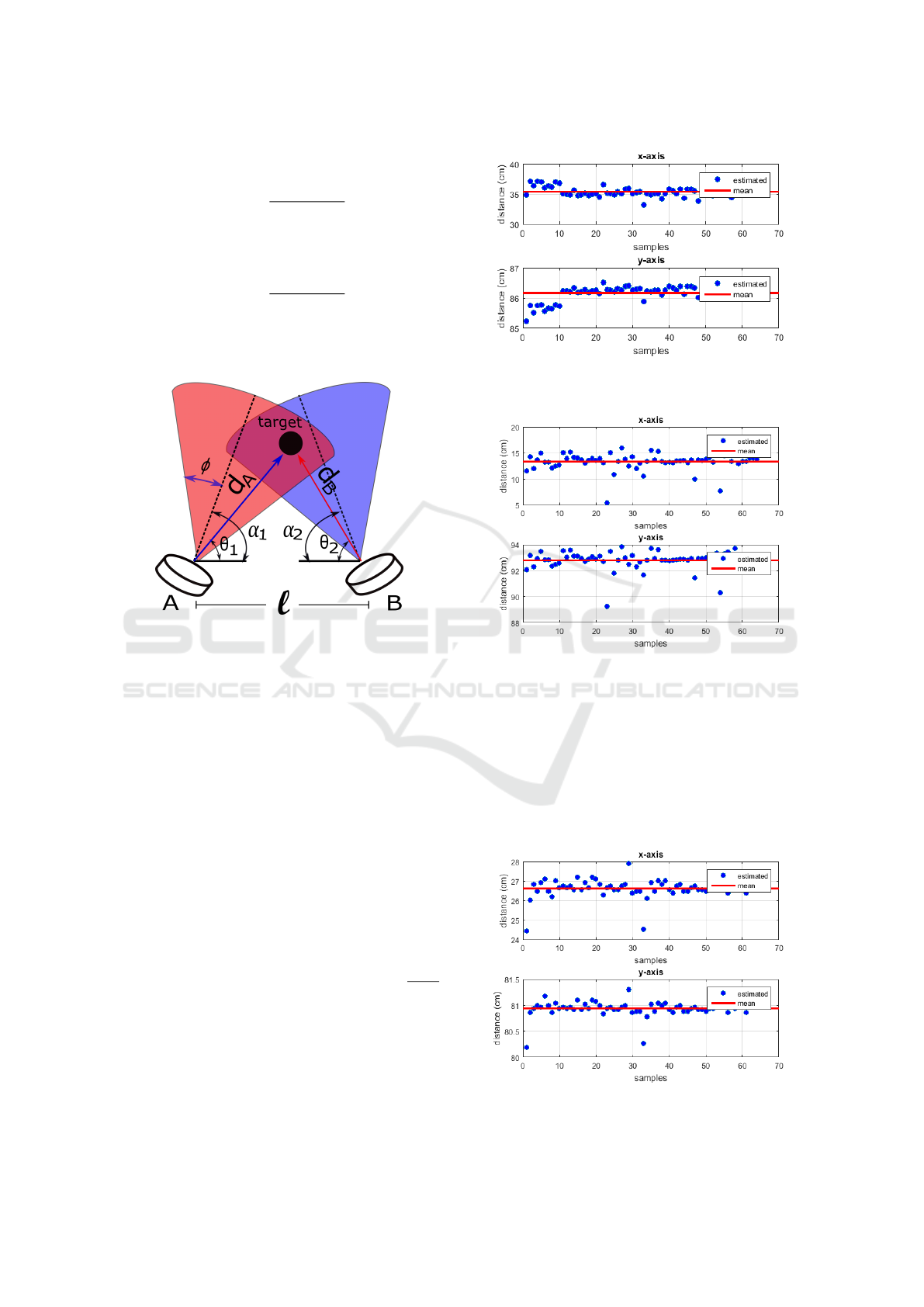
6.1 First Scenario

To perform the tests a small cardboard box was used

and the receivers were positioned with θ

1,2

= 45

◦

and

l = 51cm. Measurements were made with the object

positioned to the right, left and center of the detec-

tion area. Sixty-four samples of each position were

collected and the standard deviation (σ), mean ((x,y))

and variance (σ

) of each were calculated, as can be

seen in Table 1. Figures 12, 13 and 14 shows the vari-

ation of the samples in relation to the mean of each

measurement.

Figure 12: Dispersion of the x-axis and the y-axis samples

about the mean value of the box positioned in the right.

Figure 13: Dispersion of the x-axis and the y-axis samples

about the mean value of the box positioned in the left.

6.2 Second Scenario

Due to the fact that the raw echo signal is used, a

deeper analysis of the environment is possible. When

more than one object is present in the scene it is pos-

sible to detect it through the peaks of the envelope, as

shown in Figure 17. If two objects are very close the

Figure 14: Dispersion of the x-axis and the y-axis samples

about the mean value of the box positioned in the center.

Low-cost Sonar based on the Echolocation

823

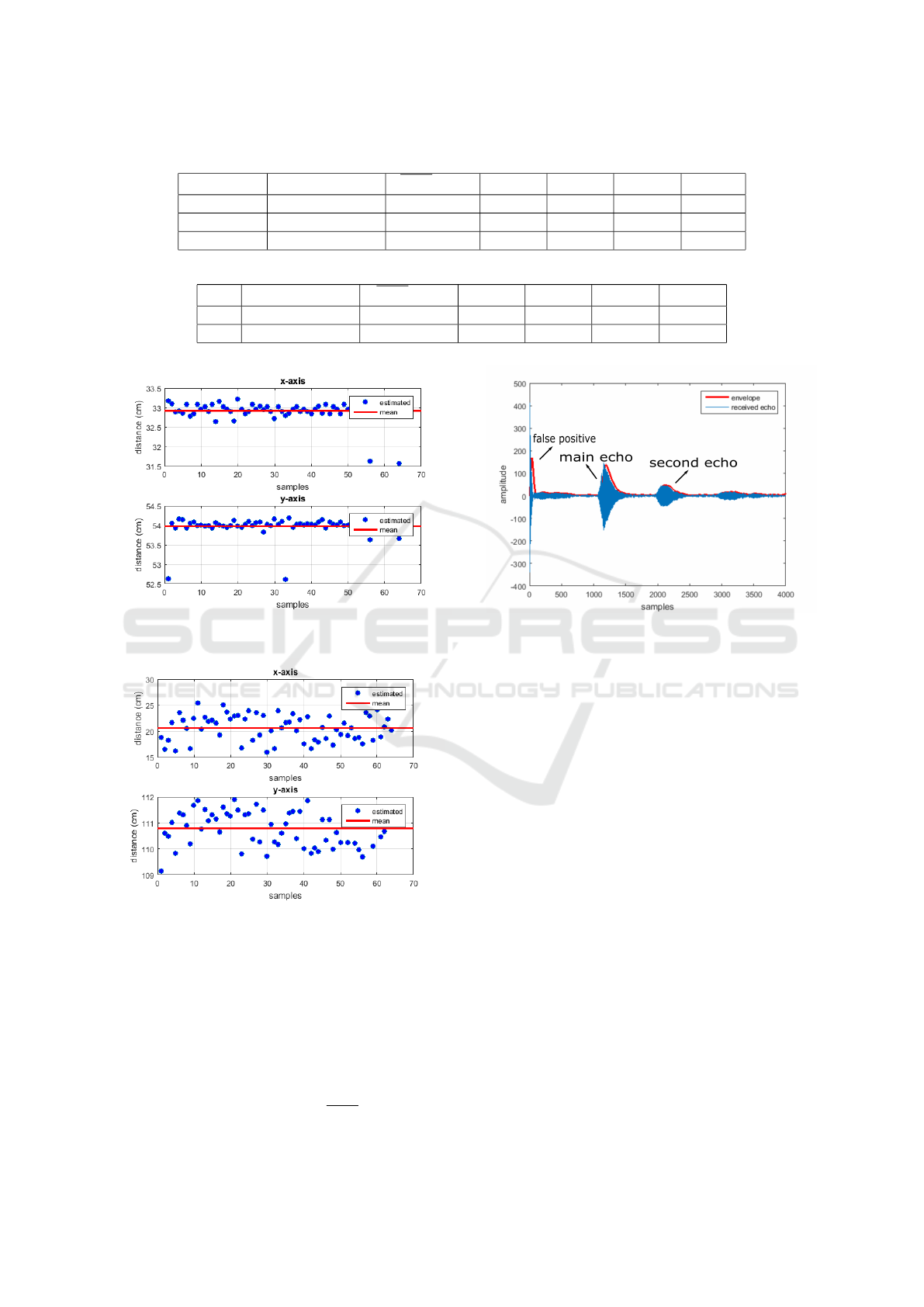
Table 1: Mean, standard deviation and variance of the ﬁrst tests.

Positioning (x,y)real* (cm) (x,y) (cm) σ

(cm) σ

(cm)

Left (11.5, 91.8) (13.3, 92.8 ) 1.66 0.71 2.76 0.50

Center (25.6, 84.5) (26.6, 80.9) 0.48 0.15 0.23 0.02

Right (35.0, 86.4) (35.3, 86.1) 0.75 0.25 0.57 0.06

Table 2: Mean, standard deviation and variance of the further tests.

Box (x,y)real* (cm) (x, y) (cm) σ

(cm) σ

(cm)

1 (35.5, 54.0) (32.9, 53.9) 0.27 0.26 0.07 0.06

2 (19.0, 111.2) (20.6, 110.8) 2.47 0.65 6.10 0.43

*Coordinates based on the object’s center.

Figure 15: Dispersion of the x-axis and the y-axis samples

about the mean value of the ﬁrst box.

Figure 16: Dispersion of the x-axis and the y-axis samples

about the mean value of the second box.

system can recognizes them as a single object. In this

way, in our test the objects were positioned far from

each other. One of the objects used was the same

one described in Subsection 6.1 and the other was a

medium cardboard box. The procedures in Subsec-

tion 6.1 were repeated. The positioning of both ob-

jects was random, the smaller box (Box 1) was closer

to the sensors and the larger box (Box 2) further away.

The standard deviation (σ), mean ((x, y)) and variance

Figure 17: Example of an echo signal received.

(σ

) of each situation are presented in Table 2. Fig-

ures 15, 16 shows the variation of the samples in rela-

tion to the mean of each measurement.

Figure 17 shows a frequent error in the receivers.

The target was more than 1 cm apart, however the sys-

tem indicated that the object was at a smaller distance.

The problem seems to occur because the echo signal

interferes with a signal that travels directly from the

transmitter to the receiver, without reﬂecting on the

object. Then, in an attempt to reduce the direct signal,

tubes were added at the receivers and at the transmit-

ter.

7 CONCLUSION AND FUTURE

WORK

The use of sonar devices is a common approach in

mobile robotics. The difﬁculty of correctly interpret-

ing the acquired data, is actually a problem. This pa-

per focused on the improvement and development of a

low cost obstacle location system based on ultrasonic

sensors and signal processing techniques.

The selection of an appropriate method to deter-

mine the accuracy of the system was one of the difﬁ-

ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics

824

culties encountered in the execution of this work. Due

to the wide beam of the sensor, the point at which

the ultrasonic wave reﬂects on the object is unknown,

made the comparison of coordinates calculated by the

system with the real coordinates a complex deﬁnition.

In Tables 1 and 2 the x and y coordinates of the

center of the object were used as real only to have a

comparison reference with the mean of the samples.

After the tests were carried out, it was veriﬁed that

all the coordinates estimated by the system were con-

tained in the established perimeter. From results, it is

clear that the system had good performance, the mean

error for the ﬁrst and second scenario was 1.68% and

1.19% respectively. The worst case occurred in the

detection of the second object, because the distance

was greater and consequently the dispersion of the

points as well.

As future work, it is intended to optimize the pro-

cessing time with another microcontroller or even a

Digital Signal Processor (DSP) for real-time applica-

tions, and embed all to some mobile navigation device

for testing and system validation. In general, the bin-

aural sensor system through the envelope extraction

can be an attractive alternative to the traditional mod-

els of ultrasonic detection, presenting good accuracy

and repeatability of the measurements.

ACKNOWLEDGEMENTS

This work is ﬁnanced by the ERDF — Euro-

pean Regional Development Fund through the Op-

erational Programme for Competitiveness and In-

ternationalisation — COMPETE 2020 Programme

within project POCI-01-0145-FEDER-006961, and

by National Funds through the FCT — Fundac¸

para a Ci

encia e a Tecnologia (Portuguese Founda-

tion for Science and Technology) as part of project

UID/EEA/50014/2013.

REFERENCES

enyi,

A. (2003). 87.47 a heron-type formula for the trian-

gle. The Mathematical Gazette, 87(509):324–326.

Cheeke, J. D. N. (2016). Fundamentals and applications of

ultrasonic waves. CRC press.

Gearhart, C., Herold, A., Self, B., Birdsong, C., and

Slivovsky, L. (2009). Use of ultrasonic sensors in

the development of an electronic travel aid. In 2009

IEEE Sensors Applications Symposium, pages 275–

280. IEEE.

Huang, K.-N. and Huang, Y.-P. (2009). Multiple-frequency

ultrasonic distance measurement using direct digital

frequency synthesizers. Sensors and Actuators A:

Physical, 149(1):42–50.

Jackson, J. C., Summan, R., Dobie, G. I., Whiteley, S. M.,

Pierce, S. G., and Hayward, G. (2013). Time-of-ﬂight

measurement techniques for airborne ultrasonic rang-

ing. IEEE transactions on ultrasonics, ferroelectrics,

and frequency control, 60(2):343–355.

Kim, H.-S. and Choi, J.-S. (2008). Advanced indoor local-

ization using ultrasonic sensor and digital compass. In

2008 International Conference on Control, Automa-

tion and Systems, pages 223–226. IEEE.

Kreczmer, B. (2010). Objects localization and differentia-

tion using ultrasonic sensors. In Robot Localization

and Map Building. IntechOpen.

Kuc, R. and Siegel, M. W. (1987). Physically based simula-

tion model for acoustic sensor robot navigation. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, (6):766–778.

Lim, J., Lee, S. J., Tewolde, G., and Kwon, J. (2014).

Ultrasonic-sensor deployment strategies and use of

smartphone sensors for mobile robot navigation in in-

door environment. In IEEE International Conference

on Electro/Information Technology, pages 593–598.

IEEE.

Marioli, D., Narduzzi, C., Offelli, C., Petri, D., Sardini, E.,

and Taroni, A. (1992). Digital time-of-ﬂight measure-

ment for ultrasonic sensors. IEEE Transactions on In-

strumentation and Measurement, 41(1):93–97.

Patkar, A. R. and Tasgaonkar, P. P. (2016). Object recog-

nition using horizontal array of ultrasonic sensors.

In 2016 International Conference on Communication

and Signal Processing (ICCSP), pages 0983–0986.

IEEE.

Peremans, H., Audenaert, K., and Van Campenhout, J. M.

(1993). A high-resolution sensor based on tri-aural

perception. IEEE transactions on Robotics and Au-

tomation, 9(1):36–48.

Popelka, M., Stru

ska, J., and Stru

ska, M. (2016). Using ul-

trasonic sensors to create 3d navigation model of area

with ultrasonic sensors. International Journal of Cir-

cuits, Systems and Signal Processing.

Queir

os, R., Martins, R., Girao, P. S., and Serra, A. C.

(2006). A new method for high resolution ultrasonic

ranging in air. Proc. international measurement con-

federation, Rio de Janeiro.

Schillebeeckx, F., De Mey, F., Vanderelst, D., and Pere-

mans, H. (2011). Biomimetic sonar: Binaural 3d lo-

calization using artiﬁcial bat pinnae. The International

Journal of Robotics Research, 30(8):975–987.

Wu, C.-J. and Tsai, C.-C. (2001). Localization of an au-

tonomous mobile robot based on ultrasonic sensory

information. Journal of Intelligent and Robotic Sys-

tems, 30(3):267–277.

Xu, B., Yu, L., and Giurgiutiu, V. (2009). Advanced meth-

ods for time-of-ﬂight estimation with application to

lamb wave structural health monitoring. In Proc. In-

ternational Workshop on SHM, pages 1202–1209.

Low-cost Sonar based on the Echolocation

825