Reducing Computational Cost in IoT Cyber Security: Case Study of

Artiﬁcial Immune System Algorithm

Idris Zakariyya

, M. Omar Al-Kadri

, Harsha Kalutarage

and Andrei Petrovski

School of Computing Science and Digital Media, Robert Gordon University, AB10 7JG, U.K.

Keywords:

Computational Cost, IoT Security, Feature Reduction, Resource Consumption, Machine Learning.

Abstract:

Using Machine Learning (ML) for Internet of Things (IoT) security monitoring is a challenge. This is due to

their resource constraint nature that limits the deployment of resource-hungry monitoring algorithms. There-

fore, the aim of this paper is to investigate resource consumption reduction of ML algorithms in IoT security

monitoring. This paper starts with an empirical analysis of resource consumption of Artiﬁcial Immune System

(AIS) algorithm, and then employs carefully selected feature reduction techniques to reduce the computational

cost of running the algorithm. The proposed approach signiﬁcantly reduces computational cost as illustrated

in the paper. We validate our results using two benchmarks and one purposefully simulated data set.

1 INTRODUCTION

IoT is expected to usher in an era of increased connec-

tivity, with an estimated 50 billion devices expected to

be connected to the Internet by 2020 (Aazam et al.,

2018). At its core, the aim of the IoT is to con-

nect previously unconnected devices to the Internet.

Thus, creating smart devices capable of collecting,

storing and sharing data, without requiring human in-

teraction. Many of these IoT devices, made up of

tiny electronic units that consume much of the avail-

able system resources, are aimed at nontechnical con-

sumers, who value low cost and ease of deployment.

This has led to some IoT manufacturers omitting criti-

cal security features, and producing insecure Internet-

connected devices. Such insecurities are often derived

and epitomized by inherent limitations of computa-

tional resources, lack of convenient user interface, use

of default credentials and insecure protocols. By com-

prising multitudes of these vulnerable IoT devices, at-

tackers can now perform large scale attacks such as

spamming, phishing and Distributed Denial of Ser-

vice (DDoS), against resources on the Internet (Mo-

ganedi and Mtsweni, 2017). IoT technology has the

potential to become a new playground for future cyber

attacks and therefore presents a number of challenges.

https://orcid.org/0000-0002-7983-1848

https://orcid.org/0000-0002-1146-1860

https://orcid.org/0000-0001-6430-9558

https://orcid.org/0000-0002-0987-2791

Several Machine Learning (ML) techniques had

been proposed for security monitoring in the spec-

trum of cyber security; however, due to the resource-

constrained nature of IoT, most of these techniques

cannot be directly deployed on these devices, mak-

ing resource management a considerably challenging

issue for IoT devices. The aim of this paper is to in-

vestigate how to reduce resource consumption of ML

algorithms in security monitoring of IoT devices. For

this purpose, we employ carefully selected feature re-

duction techniques in ML, and then empirically val-

idate our approach using the Artiﬁcial Immune Sys-

tem (AIS) algorithm utilizing two benchmark security

data sets (Meidan et al., 2018; Al Tobi and Duncan,

2018) and one carefully tailored data set. The pro-

posed approach has reduced the memory usage and

running time of the ML technique chosen in this pa-

per for security monitoring.

The rest of this paper is organized as follows. Re-

lated work is presented in Section 2. Then the the-

oretical background is presented in Section 3. The

practical experiments and results are then presented

in Section 4 and 5, respectively. Finally, a conclusion

is presented in Section 6.

2 RELATED WORK

There are various works in the ﬁeld of IoT from the

perspectives of security, architecture, deployment op-

Zakariyya, I., Al-Kadri, M., Kalutarage, H. and Petrovski, A.

Reducing Computational Cost in IoT Cyber Security: Case Study of Artiﬁcial Immune System Algorithm.

DOI: 10.5220/0008119205230528

In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 523-528

ISBN: 978-989-758-378-0

523

portunities and resources management (Farooq et al.,

2015). Authors in (Nskh et al., 2016) have employed

dimensional reduction technique with a Support Vec-

tor Machine (SVM) classiﬁer for intrusion detection

based on the KDD 99 data sets. Pajouh in (Pajouh

et al., 2016) proposed a similar method, but based on

the NSL-KDD 99 data set, and described a theoretical

approach for determining computational complexity.

Authors in (Fekade et al., 2018) and (Lopez-Martin

et al., 2017) have implemented the IoT data recovery

methods for intrusion detection. Reducing the num-

ber of features within the data set has shown an im-

proved performance. Their scheme was capable of

saving memory requirement among sensors at the ar-

chitecture level. Also, Memos in (Memos et al., 2018)

proposed an algorithm for IoT security.

An enhancement of an AIS algorithm has been

proposed in (Li

skiewicz and Textor, 2010) without

generating detectors, and the run time complexity ex-

panded from polynomial to exponential. In (Nskh

et al., 2016), there is neither experimental record for

calculating the computational complexity, nor a the-

oretical description. Most of the previous implemen-

tations were conducted using the oldest KDD 99 data

set that has been regarded as an outdated data sets.

From the literature, only a few researchers tested the

overall records of the KDD 99 data using the AIS al-

gorithm due to the implementation complexity. In this

paper, we focus on reducing the overall computational

cost of running monitoring algorithms using AIS as a

case study. The integrated resource reduction tech-

niques are capable of reducing the required memory

resources and processor running time in an embedded

IoT devices.

3 THEORETICAL

BACKGROUND

Recent development in IoT cyber security and higher

dimensionality of data resulted to the increase in vol-

ume, velocity, and variety requires careful deploy-

ment of feature reduction techniques. Promisingly,

feature reduction method can improve the efﬁciency

of ML algorithms.

3.1 Artiﬁcial Immune System

Computer scientists have been inspired by the bio-

logical systems in developing techniques for solving

problems. Pamukov in (Pamukov and Poulkov, 2017)

applied Negative Selection Algorithm (NSA) from an

AIS for IoT intrusion while, Zhuo in (Zhu et al., 2017)

employed NSA for classiﬁcation task. This algorithm,

trains a population of antibodies called detectors us-

ing a normal sample from the population. A Real

Value Negative Selection Algorithm (RNSA) gener-

ates random detectors and tests them against the sam-

ple of the self-class for afﬁnity measure. Afﬁnity is

measured based on distances as Euclidean, Manhat-

tan, or Cosine. There is no perfect shape for an an-

tibody as long as it can be implemented; however,

RNSA has been implemented using a hypersphere an-

tibody. In this work, we employed RNSA as the se-

lected AIS algorithm.

In the implementation of RNSA using real value

data sets, it makes sense to view every vector as its

location within the shape space. While working with

the data, each element in a vector corresponds to a

speciﬁc feature in the data sets. This makes it easier

to normalize the values in the data within the range of

[0, 1]; thus, each feature vector is now associated with

a point in the shape space. In the case of the RNSA al-

gorithm that handles numerical data, the shape space

(as well as the feature vector values) are continuous.

Formally, Eq. 1 has notated the RNSA.

X = R

(1)

where X ∈ {x

, x

, ..., x

} is the total sample, R

is the real valued data ﬁeld, and d is the number of

dimensions. Moreover, Y ∈ {y

, y

, ..., y

} repre-

sents the class label of the sample in a space having n

dimension.

3.2 Resource Reduction

Resource reduction is important before passing the

data to a ML algorithm. The rationale is to extract

useful features only from a huge amount of available

data, in order to alleviate over-ﬁtting and noise.

(i) Principal Component Analysis (PCA)

PCA, known as the Karhunen-Loeve, is a statis-

tical procedure that transform an observed set of

possibly correlated variables into a set of values

of linearly uncorrelated variables, called principal

components. The number of decomposed princi-

pal components are fewer than, or equal to, the

original number of variables. The rational for

PCA is to identify the subspace in which the data

clusters. For instance, an n dimensional data ob-

servation might be conﬁned into into an n −1 dis-

tinct principal components. Such capability in

data reduction, while retaining most of the vari-

ation presents in the original data, has made PCA

useful. Hong in (Hoang and Nguyen, 2018) ap-

plied PCA using substantial data sample for IoT

anomaly detection.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

524

In this research, PCA has been integrated with the

RNSA algorithm as an approach of reducing re-

source consumption in processing IoT data. The

argument raised is whether the computational cost

of applying PCA data brings any advantage in

comparison with processing the original data.

(ii) Gini Index (GI)

GI is an inductive decision tree algorithm based

on impurity function, called gini index, for ﬁnd-

ing the best split. GI method explores the rela-

tives distribution of a feature among classes and

it is a useful resource reduction method. This

technique was developed by an Italian sociologist

and statistician called Corrado Gini in 1912. The

main idea is to measure the statistical dispersion

of income across various populations. The meth-

ods has been widely adapted in the IoT research

for purifying important features as in (Liu et al.,

2018). The Gini, G for a data set S having m sub-

set S ∈ {s

, s

, ..., s

} with j different classes

C ∈ {c

, c

, ..., c

}, is deﬁned in Eq. 2.

G(S) = 1 −

∑

j=1

(2)

where, P

is the rate of class C

in S; S can be

split into n subsets, as described in Eq. 3. The

split with the best value among classes is chosen -

this process is referred to as feature impurity gain

score. The range of the splits of G

split

(S) is be-

tween [0, 1].

split

(S) =

∑

i=1

Gini(S

) (3)

In this work we integrate GI with the RNSA al-

gorithm as an approach to extract highly relevant

features in the IoT and KDD 99 data.

4 EXPERIMENTAL PROCEDURE

In the presented paper the integrated resource reduc-

tion approach has been implemented along with the

RNSA algorithm using a hypersphere. In this im-

plementation, each hypersphere present in the shape

space has the same number of dimensions as the

data. The hypersphere has been parameterized by

the length of a vector representing a record in space.

Each hypersphere is deﬁned with a real-valued radius

as well as the class label that represent the class of

a detector. The benchmark data sets investigated in

this research are real-valued and have been normal-

ized within the range of [0,1] by the Min-Max nor-

malization formula presented in Eq. 4.

Norm(x) =

x − X

min

max

− X

min

(4)

where x ∈ X represents the value of vector X ,

while X

max

and X

min

represents the maximum and

minimum values of the vector X . The normalization

helps in selecting the detector radius as the threshold

parameter used to separate normal and abnormal data.

The GI was implemented with a random forest clas-

siﬁer in selecting higher ranking features, while the

PCA implementation was designed to observe rele-

vant features with a signiﬁcant variance ratio.

The simulated artiﬁcial data, IoT-Doorbell in

(Meidan et al., 2018) and KDD-99 data sets in

(Al Tobi and Duncan, 2018), were tested and exam-

ined. The KDD and IoT data sets are publicly avail-

able for downloading from the UCI repository. The

IoT-Doorbell data set is one of the recent cyber secu-

rity data sets released in 2018 as described in (Meidan

et al., 2018). This data set has 1,572,333 data samples

and 116 features, including the class label - attacks as

’0’s, and the normal as ’1’. The records are for both

benign and malicious trafﬁc, and each record repre-

sents a trafﬁc ﬂow from a real network. The KDD-99

data set presented in has 494,022 different records for

both types of trafﬁc. The artiﬁcial data set was ran-

domly generated with 1,000 records, using the normal

distribution, and it has 2 features. A series of exper-

iments have been conducted to analyze the computa-

tional complexity with respect to the features’ contri-

bution to the resource reduction implemented in this

paper. The IoT-Doorbell data set was tested using the

full and sub-feature samples. The data set has been

checked for missing values and duplicates before the

implementation and it was splits into two portions,

80% and 20% for training and testing, respectively.

Experimental records are investigated based on

the deterministic properties of the IoT features in

terms of resource minimization, the overall amount

of IoT data, and the reductions achieved. The test

was carried out on Xeon E5 processor at 3GHz, and

the memory utilization has been observed using the

memory proﬁler of the Python module adopted. All

experiments described in this paper were conducted

using the Spyder scientiﬁc integrated Python environ-

ment.

A series of experiments have been conducted to

analyze the performance of the integrated resource re-

duction approach in terms of detection accuracy. Ex-

periments were performed ten times with the radius

varied from 0 to 1, with an increase step of 0.1. Ini-

tially, an experimental results with the artiﬁcial data

set have been examined and recorded under differ-

ent threshold values. Then, the IoT and the KDD-99

data were also tested and evaluated. The test with the

Reducing Computational Cost in IoT Cyber Security: Case Study of Artiﬁcial Immune System Algorithm

525

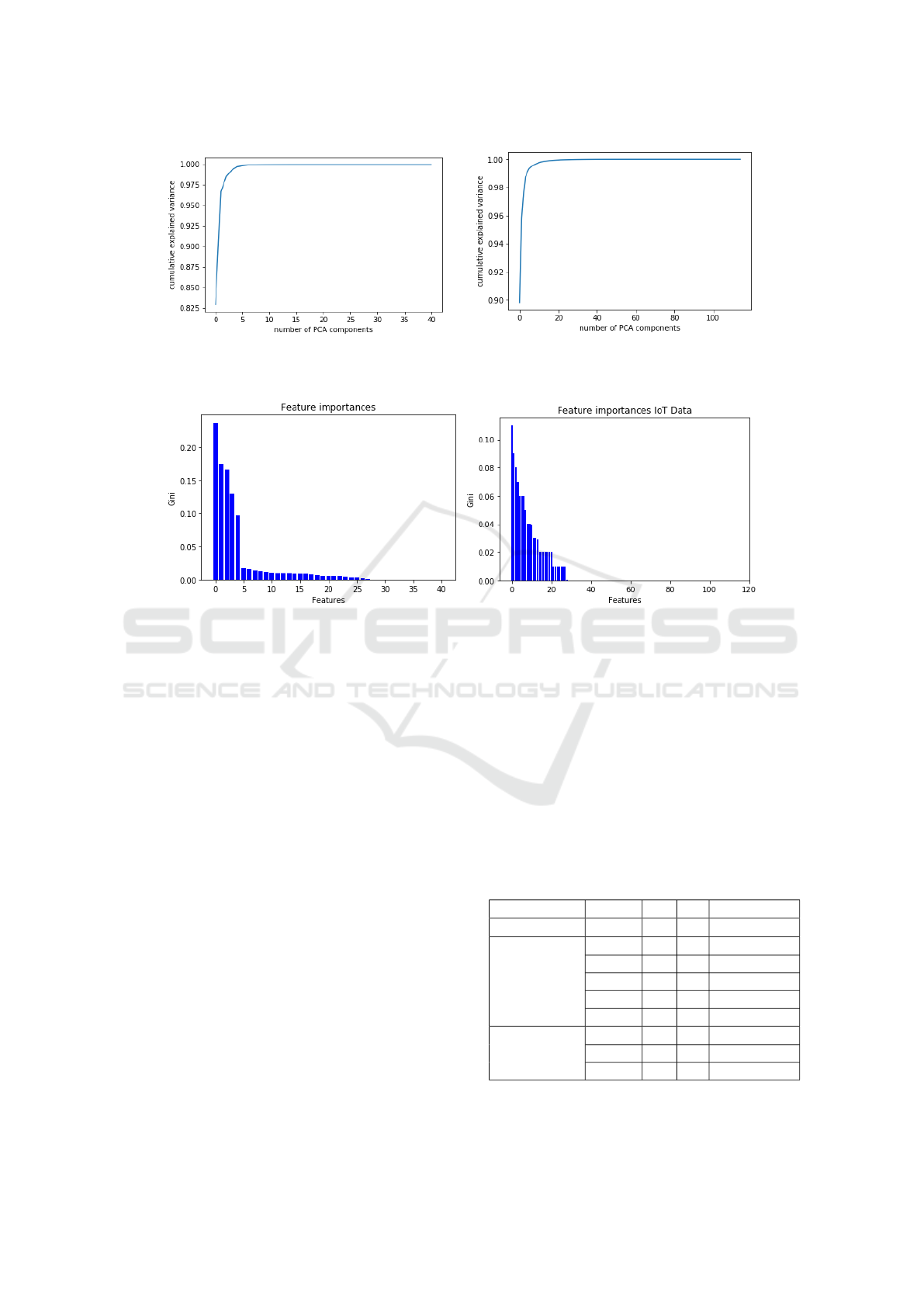
(a) (b)

Figure 1: PCA Components for (a) KDD Data and (b) IoT Data.

(a) (b)

Figure 2: Gini Index feature importance for (a) KDD Data and (b) IoT Data.

KDD-99 data was compared with the rest, where the

normal trafﬁc samples are labelled as ’1’ and all other

attack trafﬁc data are labelled as ’0’.

5 EXPERIMENTAL RESULTS

This section presents the results of the experiments

run for the implementation of the resource reduction

techniques described in this paper. Fig.1a and b il-

lustrate the PCA variance ratio of the KDD and IoT

data sets, respectively. The PCA transformation has

indicated that using only 10 to 20 principal compo-

nents from the IoT data, about 99% of the variance

ratio was retained. Moreover, Fig.2a and b illustrate

the GI features of the KDD and IoT data sets, respec-

tively. It is apparent that using only 26 GI features

from the entire IoT data can be sufﬁcient to build our

ML model.

Results in Table 1 provide the accuracy values of

the anomaly detection using the data sets considered

in this paper, with and without feature reduction. The

results reveal that the artiﬁcial data set with 2 features

has the highest accuracy of 100%. This is because the

two features are highly distinctive from each other.

Interestingly, the feature reduction techniques used on

both IoT and KDD data sets do not decrease the accu-

racy of detection compared with using the entire data

set. An equal detection accuracy of 68% is achieved

using the full data set, 10-20 PCA, and 26 GI for the

IoT data set, and an accuracy of 80% is achieved us-

ing the full data set, 5 PCA, and 11 GI for the KDD

data set. This validates the results presented in Fig. 1

and 2 and supports the argument of using feature re-

duction for resource utilization the detection accuracy

is not decreased.

Table 1: Experiments and Data Sets.

Data Sets Features PCA Gini Accuracy (%)

Synthetic Data 2 N/A N/A 100

Ba IoT

115 N/A N/A 68.30

20 X N/A 68.80

15 X N/A 68.50

10 X N/A 68.60

26 N/A X 68.50

KDD 99

41 N/A N/A 80.00

11 N/A X 80.10

5 X N/A 80.25

Table 2 provides results of the training and test-

ing memory consumption, with and without using

SECRYPT 2019 - 16th International Conference on Security and Cryptography

526

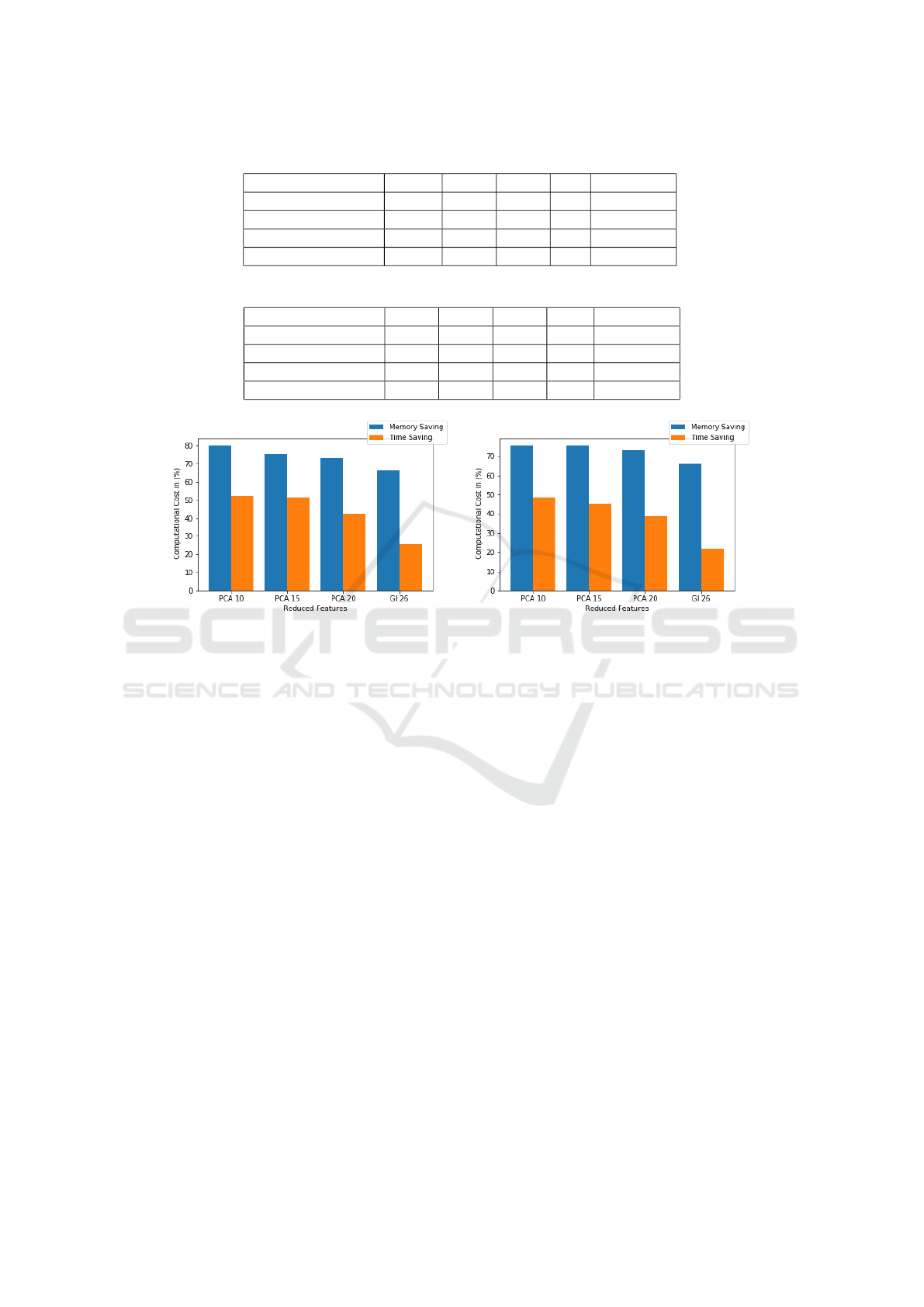
Table 2: Computational Memory Comparisons.

Computation PCA 10 PCA 15 PCA 20 GI 26 Full Features

Training in MB/Sec 233.2 285.8 317.0 393.9 1169.4

Testing in MB/Sec 233.4 286.2 317.5 396.3 1172.7

Training Saved in % 80.06 75.56 72.89 66.32 N/A

Testing Saved in % 80.09 75.59 72.93 66.21 N/A

Table 3: Computational Time Comparisons.

Computation PCA 10 PCA 15 PCA 20 GI 26 Full Features

Training in minutes 1920.2 2100.4 2340.1 3040.2 4080.2

Testing in minutes 960.6 1020.2 1140.5 1450.6 1860.2

Training Saved in % 52.0 51.4 42.6 25.5 N/A

Testing Saved in % 48.4 45.2 38.7 22.0 N/A

(a) (b)

Figure 3: Computational cost saving comparison in (a) Training and (b) Testing.

feature reduction of the IoT data set. The mem-

ory consumption for the AIS training phase using

the complete IoT data set is 1,169.4 MB/sec, com-

pared to 233.2 MB/sec using 10 PCA components,

and 393.9 MB/sec using 26 GI features. Moreover,

the memory consumption for the AIS testing using

the complete data set is 1172.7 MB/sec, compared

with 233.4 MB/sec using 10 PCA components, and

396.3 MB/sec using 26 GI features. Therefore, the

highest saving of 80% for both training and testing is

achieved by using 10 PCA, which is due to using the

lowest amount of features that capture all the variance

in the data set.

The running time of AIS algorithm, with and with-

out feature reduction, is presented in Table 3. Consid-

ering the 10, 15, and 20 PCA components and the 26

GI features, the running time is lowest in the case of

using 10 PCA components compared with the remain-

ing feature reduction approaches, with a total saving

of 52% and 48% for the training and testing phases,

respectively. The resulting saving of both memory

consumption and processing time is presented in Fig.

The analyzed results reveal considerable reduc-

tions in the memory consumption and processing

time when using smaller data features. These results

demonstrate the capability of the proposed approach

in utilizing and managing ML resources.

6 CONCLUSION

In this paper, resource utilization for lower computa-

tional cost of ML algorithms in IoT security monitor-

ing is investigated. This is based on feature reduction

methods, particularly the principal component anal-

ysis and Gini index techniques. An empirical vali-

dation of the proposed approach was presented using

the Artiﬁcial Immune System (AIS) algorithm, utiliz-

ing two benchmark security data sets, which are the

KDD 99 and IoT-Doorbell, and one carefully tailored

data set.

Results have demonstrated that feature reduction

techniques have lead to signiﬁcant savings on both

memory consumption and processing time. The high-

est saving occurred by using 10 PCA components,

compared with 15 and 20 PCA components, and GI

techniques. The savings have reached up to 80%

and 52% for memory consumption and processing

time, respectively. Providing recommendation of us-

Reducing Computational Cost in IoT Cyber Security: Case Study of Artiﬁcial Immune System Algorithm

527

ing PCA over GI for further feature reduction and

computational cost savings for the considered scenar-

ios.

REFERENCES

Aazam, M., St-Hilaire, M., Lung, C.-H., Lambadaris, I.,

and Huh, E.-N. (2018). Iot resource estimation chal-

lenges and modeling in fog. In Fog Computing in the

Internet of Things, pages 17–31. Springer.

Al Tobi, A. M. and Duncan, I. (2018). Kdd 1999 genera-

tion faults: A review and analysis. Journal of Cyber

Security Technology, 2(3-4):164–200.

Farooq, M. U., Waseem, M., Khairi, A., and Mazhar, S.

(2015). A critical analysis on the security concerns

of internet of things (iot). International Journal of

Computer Applications, 111(7).

Fekade, B., Maksymyuk, T., Kyryk, M., and Jo, M. (2018).

Probabilistic recovery of incomplete sensed data in

iot. IEEE Internet of Things Journal, 5(4):2282–2292.

Hoang, D. H. and Nguyen, H. D. (2018). A pca-based

method for iot network trafﬁc anomaly detection. In

IEEE 20th ICACT, pages 381–386.

skiewicz, M. and Textor, J. (2010). Negative selection

algorithms without generating detectors. In ACM

GECCO, pages 1047–1054. ACM.

Liu, H., Zhou, M., Lu, X. S., and Yao, C. (2018). Weighted

gini index feature selection method for imbalanced

data. In IEEE ICNSC, pages 1–6.

Lopez-Martin, M., Carro, B., Sanchez-Esguevillas, A., and

Lloret, J. (2017). Conditional variational autoencoder

for prediction and feature recovery applied to intru-

sion detection in iot. Sensors, 17(9):1967.

Meidan, Y., Bohadana, M., Mathov, Y., Mirsky, Y., Shab-

tai, A., Breitenbacher, D., and Elovici, Y. (2018). N-

baiot—network-based detection of iot botnet attacks

using deep autoencoders. IEEE Pervasive Computing,

17(3):12–22.

Memos, V. A., Psannis, K. E., Ishibashi, Y., Kim, B.-G.,

and Gupta, B. B. (2018). An efﬁcient algorithm for

media-based surveillance system (eamsus) in iot smart

city framework. Future Generation Computer Sys-

tems, 83:619–628.

Moganedi, S. and Mtsweni, J. (2017). Beyond the conve-

nience of the internet of things: Security and privacy

concerns. In IEEE IST-Africa, pages 1–10.

Nskh, P., Varma, M. N., and Naik, R. R. (2016). Princi-

ple component analysis based intrusion detection sys-

tem using support vector machine. In IEEE RTEICT,

pages 1344–1350.

Pajouh, H. H., Javidan, R., Khayami, R., Ali, D., and Choo,

K.-K. R. (2016). A two-layer dimension reduction and

two-tier classiﬁcation model for anomaly-based intru-

sion detection in iot backbone networks. IEEE TETC.

Pamukov, M. E. and Poulkov, V. K. (2017). Multiple

negative selection algorithm: Improving detection er-

ror rates in iot intrusion detection systems. In IEEE

IDAACS, volume 1, pages 543–547.

Zhu, F., Chen, W., Yang, H., Li, T., Yang, T., and Zhang,

F. (2017). A quick negative selection algorithm for

one-class classiﬁcation in big data era. Mathematical

Problems in Engineering, 2017.

SECRYPT 2019 - 16th International Conference on Security and Cryptography

528