Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space

Exploration: A* Tie-breaking

Thomas Rathfux

, Hermann Kaindl

, Ralph Hoch

and Franz Lukasch

Institute of Computer Technology, TU Wien, Austria

Robert Bosch AG, Goellnergasse 15-17, Vienna, Austria

Keywords:

Design Space Exploration, Best-ﬁrst Search, A* Tie-breaker.

Abstract:

Using design space exploration (DSE), certain real-world problems can be made solvable through (heuristic)

search. A meta-model of the domain and transformation rules deﬁned on top of it specify the search space.

For example, we previously (meta-)modeled speciﬁc problems in the context of reusing hardware/software

interfaces (HSIs) in automotive systems, and deﬁned transformation rules that lead from a model of one

speciﬁc HSI to another one. Based on that, a minimal number of adaptation steps can be found using best-ﬁrst

A* searches that lead from a given HSI to another one fulﬁlling new requirements. A closer look revealed

that these problems involved a few reconﬁgurations, but often no reconﬁguration is necessary at all. For such

trivial problem instances, no real search should be necessary, but in general, it is. After it became clear that a

good tie-breaker for the many nodes with the same minimal value of the evaluation function of A* was the key

to success, we performed experiments with the tie-breakers recently found best in the literature, all based on a

last-in-ﬁrst-out (LIFO) strategy in contrast to the previous belief that using minimal h-values would be the best

tie-breakers. However, our experiments provide empirical evidence in our real-world domain that tie-breakers

based on minimal h-values can indeed be (statistically signiﬁcantly) better than a tie-breaker based on LIFO.

In addition, they show that the best tie-breakers for the more difﬁcult problems are also best for the trivial

problem instances without reconﬁgurations, where they really make a difference.

1 INTRODUCTION

In previous work (Rathfux et al., 2019), we presented

an experimental evaluation of design space explo-

ration (DSE) of Hardware/Software Interfaces (HSIs)

in automotive systems based on the VIATRA2 tool

as-is (Bergmann et al., 2015). We used the best-ﬁrst

search algorithm A* (Hart et al., 1968) to ﬁnd opti-

mal solutions for problems stated through given real-

world requirements, after having intuitively deﬁned

an admissible heuristic. According to our best knowl-

edge, this was the ﬁrst search approach based on de-

sign space exploration in the automotive domain.

A closer look revealed that these problems in-

volved a few reconﬁgurations, but often no reconﬁg-

uration is necessary at all. However, for such trivial

problem instances, no real search should be necessary,

but in general, it is.

The question arose how to handle problems where

sometimes search is required and often not. First,

we considered special-purpose approaches for these

kinds of problems, including iterative-deepening

depth-ﬁrst search using bounds determined through

the admissible heuristic that we deﬁned.

Reconsidering the optimality results for A*

(Dechter and Pearl, 1985), we had a closer look into

different tie-breakers of A* for nodes with the same

minimal value of its evaluation function. In fact, our

problems involve unit costs, so that there are usu-

ally many nodes with the same value. In particu-

lar, we conjectured that a last-in-ﬁrst-out (LIFO) tie-

breaker could improve on the default tie-breaker of

the VIATRA2 tool. This led us to our ﬁrst research

question addressed in this paper:

RQ1: Can a LIFO tie-breaker signiﬁcantly im-

prove the search efﬁciency of A* as compared to the

default tie-breaker of the VIATRA2 tool?

Since recent work in the literature (as reviewed

below) showed renewed interest in A* tie-breaking as

well, we made experiments with different tie-breakers

for A* for investigating this research question as well

as statements found in the literature. The latter led to

our second research question:

RQ2: Is a LIFO tie-breaker generally better in

Rathfux, T., Kaindl, H., Hoch, R. and Lukasch, F.

Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space Exploration: A* Tie-breaking.

DOI: 10.5220/0008119405950604

In Proceedings of the 14th International Conference on Software Technologies (ICSOFT 2019), pages 595-604

ISBN: 978-989-758-379-7

595

terms of A* search efﬁciency than a tie-breaker using

minimal heuristic values?

In order to systematically study the difﬁculty of

randomly determined problem instances, we deﬁned

(simple) metrics for problem difﬁculty. For making

sure that chance ﬂuctuations may not lead to wrong

interpretations of the results, we also used the sign

test for testing statistical signiﬁcance.

The remainder of this paper is organized in the fol-

lowing manner. First, we sketch some background on

the real-world domain and the search space deﬁned

as well as on the DSE tool providing the search in-

frastructure, and on heuristic search for optimal solu-

tions using A*. Then we specify the goal condition

in this speciﬁc application domain. Based on that, we

formally specify the admissible heuristic function re-

quired for A* to ﬁnd and guarantee optimal solutions.

Having explained all the prerequisites, we present our

experiment and its results, with a focus on problem

difﬁculty and different tie-breakers for A*. Finally,

we relate this to previous work on A* tie-breaking

and discuss interesting observations on differences

between our results and those in previous work.

2 BACKGROUND

First, in order to make this paper self-contained, we

sketch the domain of Electronic Control Units (ECUs)

that our HSIs are implemented on, and the essence of

the HSIs themselves as far as needed, as well as the

resulting search space. Then we refer to the model-

driven tool VIATRA2, which we use for design space

exploration. Since we perform this exploration using

heuristic search, we also explain it here brieﬂy.

2.1 Domain and Search Space

Our DSE approach is used for ﬁnding optimal so-

lutions for Hardware/Software Interfaces (HSIs) on

ECUs in the automotive domain. Each ECU provides

an HSI through which external hardware components

can communicate with internal software functions.

The software of these ECUs runs on a microcontroller

with internal resources, and the external hardware

components require some of them for functioning as

needed. In addition, hardware components may be

placed on the ECU to pre-process signals from exter-

nal hardware, so that they can be mapped to or access

resources. The external hardware is connected to the

ECU via pins, and the ECU-pins are routed through

hardware components on the ECU to pins of the mi-

crocontroller (µC-pin). Each µC-pin is internally con-

nected to several resources, e.g., an Analog-Digital-

Converter (ADC). The hardware components together

with selected resources on connected µC-pins provide

a speciﬁc interface type on an ECU-Pin, which an ex-

ternal hardware can use. All the selected interface

types together specify the HSI.

External hardware requires certain functionality

on ECU-pins for functioning as needed. Thus, they

specify requirements that an ECU and its HSI have

to fulﬁll. An ECU is only satisfactory for the cus-

tomer if all requirements of all external hardware are

met. To fulﬁll requirements, speciﬁc types of re-

sources in the microcontroller (µC-Resources) have

to be made available to ECU-pins via hardware com-

ponents. The connections of ECU-pins to hardware

components and from hardware components to µC-

pins are ﬁxed. Each µC-pin is connected to several

µC-Resources, but only one of them can be used at

the same time. However, which µC-Resource is se-

lected on a speciﬁc ECU is variable and can be conﬁg-

ured. Hence, this variability provides options to fulﬁll

requirements. In essence, this variability deﬁnes the

search space.

Figure 1 illustrates schematically how this search

space is deﬁned. It shows the requirements on the left,

e.g., R1, the ECU-pins, e.g., 0, the hardware com-

ponents, e.g., HWC1, and the available types of µC-

Resources on the right, e.g., DS

ADC. The ACSx and

ACx layers can be ignored for now, as they depict in

our model what kind of interface types can be made

available to external hardware. In essence, only the

selection of concrete µC-Resources on a speciﬁc µC-

pin is variable and can be changed. Thus, the selec-

tion of a concrete µC-Resource deﬁnes a transforma-

tion from one state in our search space to another one.

This domain knowledge is captured in the meta-

model published in our previous work (Rathfux et al.,

2019).

2.2 VIATRA2

VIATRA2 is a model-driven framework for design

space exploration. Based on such a meta-model,

this framework supports deﬁning search strategies for

traversing the design space, starting from an initial

model by applying transformation rules. VIATRA2

also allows deﬁning such rules based on the meta-

model used. They are applied throughout the search

to explore the design space. Goals are deﬁned as con-

ditions that must be satisﬁed for a solution.

VIATRA2 as used in our work presented here, is

actually just one tool of a set of tools developed over

time, where different tools provide different tech-

niques for design space exploration (Bergmann et al.,

2015).

ICSOFT 2019 - 14th International Conference on Software Technologies

596

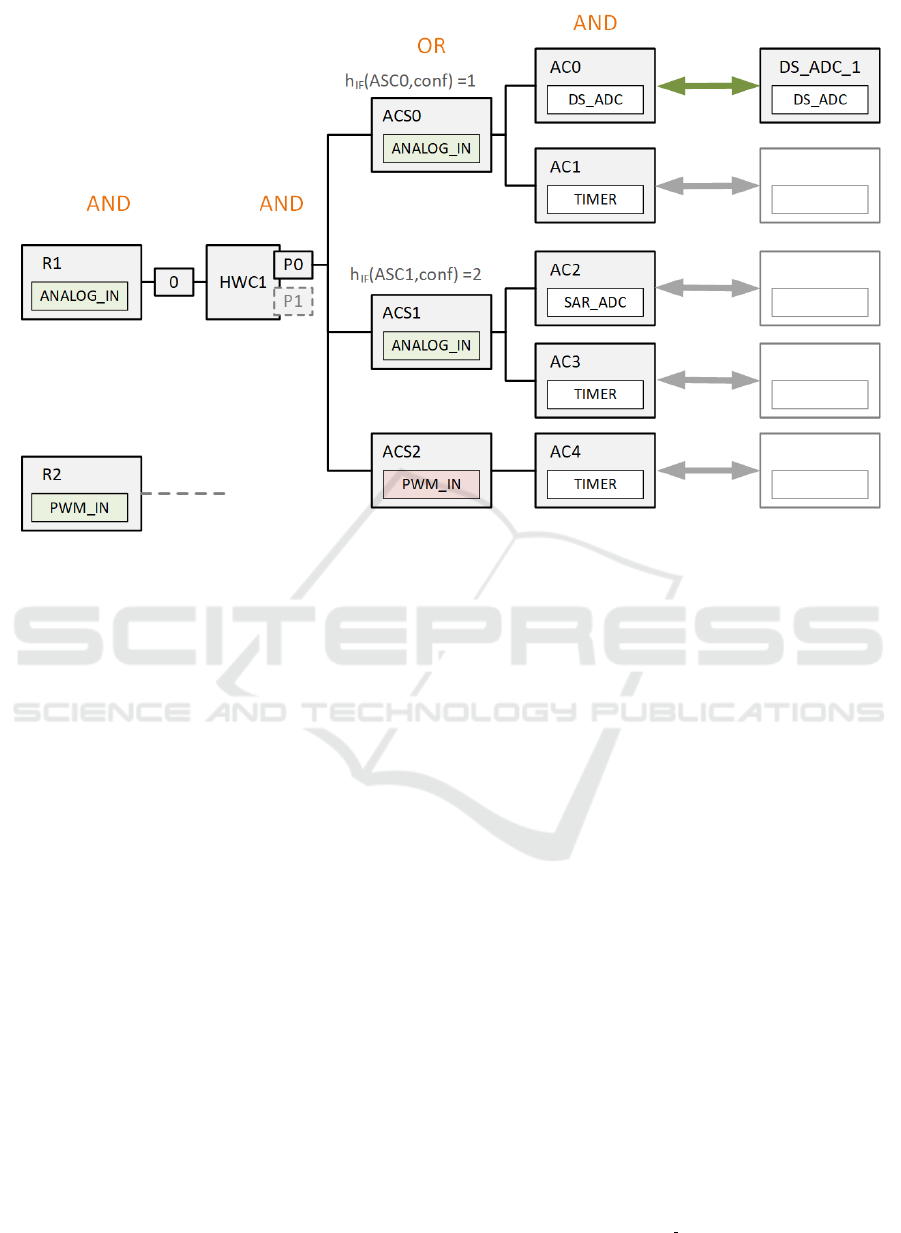
Figure 1: A requirement condition and its possible fulﬁllments based on a partial conﬁguration.

2.3 Heuristic Search for Optimal

Solutions

Many search algorithms have been presented in the

literature, so it would be prohibitive to review all of

them here. Rather, we focus on the one used in the ex-

periment reported in this paper, A*, a (unidirectional)

search algorithm with certain optimality guarantees.

The traditional best-ﬁrst search algorithm A*

(Hart et al., 1968) maintains the set OPEN of so-called

open nodes that have been generated but not yet ex-

panded, i.e., the frontier nodes. Much as any best-

ﬁrst search algorithm, it always selects a node from

OPEN with minimum estimated cost, one of those it

considers “best”. This node is expanded and moved

from OPEN to CLOSED. A* speciﬁcally estimates the

cost of some node n with an evaluation function of

the form f (n) = g(n) + h(n), where g(n) is the (sum)

cost of a path found from s to n, and h(n) is a heuris-

tic estimate of the cost of reaching a goal from n, i.e.,

the cost of an optimal path from s to some goal t. If

h(n) never overestimates this cost for all nodes n (it

is said to be admissible) and if a solution exists, then

A* is guaranteed to return an optimal (minimum-cost)

solution (it is also said to be admissible). Under cer-

tain conditions, A* is optimal over admissible unidi-

rectional heuristic search algorithms using the same

information, in the sense that it never expands more

nodes than any of these (Dechter and Pearl, 1985).

3 GOAL CONDITION

A formal speciﬁcation of goal conditions can be given

in ﬁrst order logic. As each requirement is speci-

ﬁed as a speciﬁc interface type IF(i f ) at a speciﬁc

ECU-pin p, we introduce a requirement predicate

REQ(p, IF(i f )).

Each hardware component may support several in-

terface types on its ports. Hence, we introduce a pred-

icate HW (p, IF(i f ), port), which connects an ECU-

pin to the hardware component and the supported in-

terface at a speciﬁc port. At each port, there may be a

variety of supported interface types. If a speciﬁc inter-

face type is supported, then an assignment constraint

set has to be deﬁned for it, i.e., ACS(port, IF(i f )).

These assignment constraint sets are or-connected:

port

∈Port

(ACS(port

, IF(i f ))) (1)

One assignment constraint set is speciﬁed by

and-connected assignment constraints, i.e.,

AC(RType(RT ), SR(R)), where RType denotes

the requested resource type and SR speciﬁes if a

resource has been selected:

ACS(port, IF(i f )) =

rt∈REQ RES

i f

AC(RType(RT

), SR(R

))

(2)

Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space Exploration: A* Tie-breaking

597

A port supports an interface type if there exists at

least one ACS that fulﬁlls its requirements. Hence,

the interface types of all ports of a hardware compo-

nent are deﬁned as:

port

∈Port

(ACS(port

, IF(i f )) (3)

Hence, a speciﬁc interface type at a port of a hard-

ware component is deﬁned as:

HW (p, IF(i f ), port) =

acs∈port

(ACS

acs

(port, IF(i f ))

(4)

Using these formulas, we can formally specify

that a requirement is fulﬁlled if a connected hardware

component exists that provides the interface type on a

port:

REQ(p, IF(i f )) = HW (p, IF(i f ), port) (5)

Based on this formula, our goal condition is a

conjunction of all requirements and all ports on con-

nected hardware components for a speciﬁc interface

type.

i f ∈Req IF

p∈HW P

i f

(

port

∈Port

ACS(port

, IF(i f ))) (6)

4 ADMISSIBLE HEURISTIC

FUNCTION

For A*, admissibility of the heuristic function is im-

portant for guaranteeing the optimality of solutions

found. For evaluating a conﬁguration in such a func-

tion with respect to its goal achievement, the number

of not (yet) fulﬁlled conjunctively related goal condi-

tions is counted. In case of disjunctively related con-

ditions, the minimum is taken. The resulting number

can be used as the heuristic value, since each condi-

tion needs at least one application of a transformation

rule. In fact, these can only be activation rules. De-

activation rules may additionally be necessary, in or-

der to deactivate some connection so that another one

needed can be activated at this particular pin. Conse-

quently, this number is less than or equal to the num-

ber of minimal steps to achieve the goal condition,

i.e., this is an admissible heuristic.

This can also be explained more theoretically

based on the meta-heuristic of problem relaxation, see

(Pearl, 1984). A relaxed problem would only need ac-

tivation rules for its solution, i.e., the number calcu-

lated by our heuristic function.

Let us illustrate this in detail using a speciﬁc ex-

ample. As already mentioned in the introduction, in

an automotive system like a car, a pedal position sen-

sor is connected to the corresponding ECU. We elab-

orate on the calculation of our heuristic function for

the case of an analogue signal delivered by the sen-

sor. Figure 1 illustrates this example through a re-

quirement condition R1 (at the left) and its possible

fulﬁllments (in the middle) based on a partial conﬁg-

uration (at the right).

The heuristic function optimistically estimates the

distance from a given conﬁguration to a goal by cal-

culating the minimal number of transformation steps

necessary to reach a conﬁguration that fulﬁlls the goal

condition. We explain this using a part of a goal

condition, where the clause of its conjunction corre-

sponding to R1 (as shown in Figure 1) is deﬁned for

this example as

REQ(0, IF(ANALOG IN))

Formally, this means a disjunction of

ACS(P0, IF( )) instantiated for ACS0, ACS1

and ACS2. However, ACS2 has to be discarded,

since its interface type PWM IN is different from the

required ANALOG IN. Of course, only assignment

constraint sets with matching interface types are

taken into account.

The remaining formula can be written as follows,

according to the concrete example shown in Figure 1:

(AC(RType(DS ADC), SR(DS ADC 1))∧

AC(RType(T IMER), SR(Empty)))

∨

(AC(RType(SAR ADC), SR(Empty))∧

AC(RType(T IMER), SR(Empty)))

(7)

SR(DS ADC 1) means that the concrete resource

DS ADC 1 is selected for the assignment constraint

AC0 as shown in the ﬁgure. Since the type of the

selected resource matches the required resource type

of the assignment constraint, the predicate AC evalu-

ates to true for this example. Empty as given for the

other assignment constraints in this example means

that no resource is selected (yet) for them. Therefore,

the predicate AC for these examples evaluates to false.

This deﬁnes the current partial conﬁguration in the

course of the search that is evaluated heuristically.

For such a partial conﬁguration, the correspond-

ing formula evaluates to false. In order to fulﬁll the

goal condition, all the remaining and-connected parts

need to evaluate to true as well. This requires certain

transformation steps, and for calculating the admissi-

ble heuristic, we determine the minimum number of

such steps.

ICSOFT 2019 - 14th International Conference on Software Technologies

598

In fact, for making a single AC from false to

true, at least a single transformation step is necessary.

Note, that a single step cannot make more than one

AC true according to the deﬁnition of the transforma-

tion rules based on the meta-model.

We deﬁne a heuristic function h

of a spe-

ciﬁc interface type for a given conﬁguration

(ASCS

,CONF)) in such a way, that it never

over-estimates the minimum number of steps for ful-

ﬁlling the requirements of the interface type. Hence,

for or-connected parts, it is necessary to take the min-

imum, so that the heuristic estimate is optimistic. In

the example, therefore, h

(ASC0, con f ) = 1 must be

taken for port P0.

For calculating the complete heuristic function for

a given conﬁguration con f , all requirements and as-

sociated ports must be taken into account. A conﬁgu-

ration is speciﬁed by all currently selected resources.

Therefore, the heuristic function can be calculated as

follows:

h(con f ) =

∑

r∈Req

∑

p∈Ports(r)

min

acs∈ACS(p,IF(r))



(acs, con f )



(8)

5 EXPERIMENT

First, we present our design of the experiment, and

then its results.

5.1 Experiment Design

Since statistical ﬂuctuation was to be expected for dif-

ferent problem instances in the experiment, we de-

ﬁned several ones and included some randomness into

their creation, in order to avoid bias. In addition, we

wanted to systematically get data on the average run-

ning times for different (optimal) solution lengths, in

order to evaluate the effect of scaling with increasing

problem difﬁculty.

Then we created problem instances with different

solution lengths by generating requirements randomly

(again). This resulted in 75 problem instances for

each solution length, with different starting conﬁgura-

tions and different target requirements. From this set,

ten problem instances each were selected randomly

and used for the searches in the experiment. Since we

experienced some variation in the runs of VIATRA2

also regarding the ordering during design space ex-

ploration (i.e., some indeterminism coming from the

tool), which inﬂuences the running time depending

on when a solution is found, we ran each problem in-

stance ten times.

The problems created randomly had different dif-

ﬁculty in terms of reconﬁgurations required. For sys-

tematically studying the effect of problem difﬁculty

on the search efﬁciency, we deﬁne two difﬁculty met-

rics as given in Equations 9 and 10. These metrics

can only be calculated in hindsight, of course, after

both the heuristic value h(s) of the start node s and the

real optimal length C

is known, but this is sufﬁcient

for studying the results of various searches. These

metrics do not purely measure the difﬁcult of a given

problem per se, but relative to a given heuristic h and,

of course, the problem difﬁculty also depends directly

on the optimal solution length C

as investigated be-

low. Still, we prefer such measures to the approach of

sorting problem instances according to the effort that

a particular algorithm has to solve them. In the fol-

lowing, we only make use of d

abs

in absolute terms,

since it appears to ﬁt better in our context, but for

other problems, d

rel

in relative terms may be more

appropriate.

abs

(s) = C

− h(s) (9)

rel

(s) =

abs

(s)

C∗

(10)

Since our research questions are about search efﬁ-

ciency, we deﬁned dependent variables for measuring

it:

• running time,

• number of states visited.

In order to perform statistical tests, we may con-

sider the null hypothesis that two algorithms to be

compared perform equally well (according to a given

criterion). The resulting p-value gives the probabil-

ity that the data are consistent with the null hypoth-

esis that each method is equally good. Therefore,

only small numbers (below 0.05, for example), indi-

cate that the difference is unlikely to be from chance

ﬂuctuation (the null hypothesis is to be rejected).

We may say that algorithm A “wins” against B

in experiment i when for the corresponding depen-

dent variables a

< b

holds. For testing the statistical

signiﬁcance of results about the number of cases in

which one algorithm wins, we consider the null hy-

pothesis that the number of wins is a random event

with probability

. The sign test is appropriate here,

especially since it requires no speciﬁc assumptions

about distributions of the samples. Much as for our

previous search experiments, e.g., in (Kaindl et al.,

1995) for unidirectional search and in (Kaindl and

Kainz, 1997) for bidirectional search, we apply the

sign test for our current experiments as well.

Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space Exploration: A* Tie-breaking

599

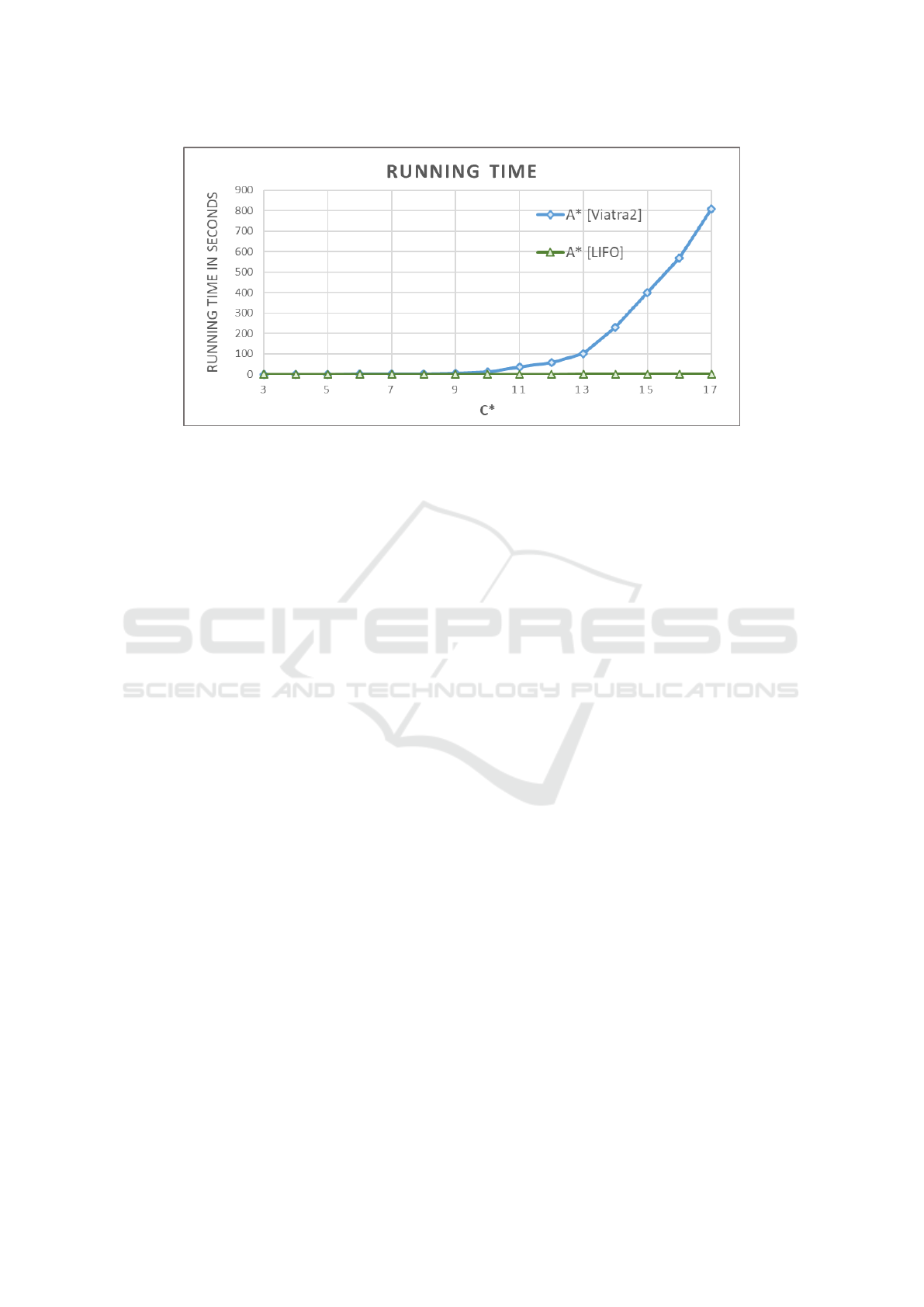
Figure 2: Running times for trivial problems with d

abs

(s) = 0.

We executed the experiment runs on a standard

Windows laptop computer with an Intel Core i7-

8750H Processor (9MB Cache, up to 4.1 GHz, 6

Cores). It has a DDR4-2666MHz memory of 32GB.

The disk does not matter, since all the experimental

data were gathered using the internal memory only.

5.2 Results

On the laptop computer used, we ﬁrst addressed RQ1

and collected the results of searches with optimal so-

lution lengths (costs) C* for A* with two different

tie-breakers involved, the default one implemented

in VIATRA2, and another one selecting strictly ac-

cording to LIFO from the list of currently minimal f -

values. All the searches found optimal solutions and

guaranteed that they are optimal (in terms of solution

length).

Figure 2 shows the mean running times in

seconds (when no other processes were running

on the laptop computer used) for trivial problems

without any reconﬁgurations, i.e., d

abs

(s) = 0.

A* [VIATRA2] is the standard implementation in

VIATRA2. It mimics an “arbitrary” selection from

all the ties as indicated in the original deﬁnition

of A* by using the PriorityQueue described at

https://docs.oracle.com/javase/10/docs/api/java/util/

PriorityQueue.html. Its scaling behavior is a bit

strange, given that these problems are actually trivial.

A* [LIFO], in contrast, can exploit that fact and

is very efﬁcient on this class of problems. Note,

that A* [FIFO] (using a ﬁrst-in-ﬁrst-out strategy

for tie-breaking) is even much worse than A*

[VIATRA2].

Of course, A* [LIFO] (abbreviated in the follow-

ing ﬁgures and tables as [LIFO]) cannot have such

an excellent search efﬁciency with increasing prob-

lem difﬁculty. This is clearly shown in Figure 3 (with

the broken lines) for d

abs

= 0, 1, 2, and a mix that tries

to model the distribution of problem difﬁculty in prac-

tice. More precisely, it means that 60 percent would

have d

abs

= 0, 20 percent d

abs

= 1, and 20 percent

abs

= 2. d

abs

is abbreviated in all the ﬁgures as d.

Generally, the LIFO tie-breaker makes A* also

more efﬁcient than A* [VIATRA2] (the default tie-

breaker in VIATRA2) on more difﬁcult problems, as

indicated by the red square in Figure 3. Hence, we

claim that our experiments provide enough evidence

for answering RQ1 afﬁrmatively. That is, a LIFO

tie-breaker can signiﬁcantly improve the search efﬁ-

ciency of A* as compared to the default tie-breaker of

the VIATRA2 tool.

For practical purposes, this improvement through

the simple LIFO tie-breaker seemed already sufﬁcient,

and the latest literature (Asai and Fukunaga, 2017)

on tie-breakers for non-zero-cost domains even sug-

gested that it could be the best strategy, anyway. Still,

we found it interesting to investigate on the efﬁciency

of h-based tie-breakers, which have been heavily used

in the past (see below for this related work). This is

what our RQ2 is all about.

Hence, we also compared A* using LIFO with an-

other tie-breaker that ﬁrst uses smallest h-values to

break ties (as a primary tie-breaker), and applies a

LIFO tie-breaking policy only as a second-level cri-

terion. Figure 3 also shows a comparison of these tie-

breakers. It indicates that A* [h, LIFO] could be even

more efﬁcient than A* [LIFO] for our problems and

using this heuristic.

This result indicated to answer our RQ2 with no.

However, simply comparing the mean values may have

been misleading, since the results could have come

from chance ﬂuctuation. Hence, as sketched above,

we employed the sign test (using SPSS) for investi-

ICSOFT 2019 - 14th International Conference on Software Technologies

600

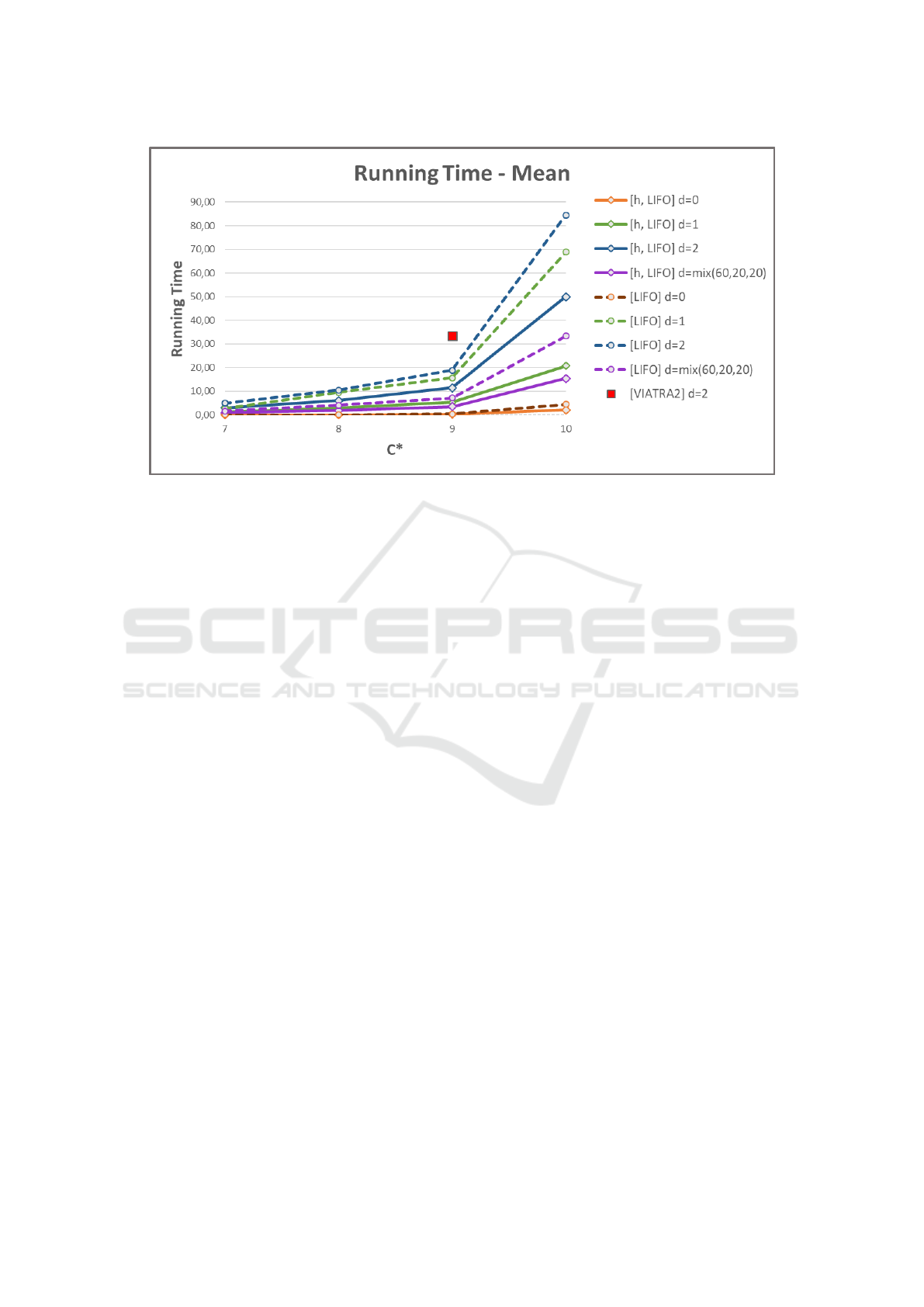
Figure 3: Mean running times of using LIFO as a primary vs. a secondary tie-breaker after minimal h-values on problems

with d

abs

(s) ≥ 0.

gating that. More precisely, we tested the null hy-

pothesis that the median of the differences between

the running times of A* [h, LIFO] and A* [LIFO] is

0, on a signiﬁcance level of .05. This null hypothe-

sis can be rejected. Therefore, it is unlikely that the

difference comes from chance ﬂuctuation.

Since tie-breaking using h-values did so well here,

the question remained how well it would do with FIFO

or the default VIATRA2 tie-breaker as a secondary

tie-breaker each. The differences between the running

times when using different secondary tie-breakers are

small, as long as the primary h-based tie-breaker is

used. This may be a result of ﬂuctuations regarding

running times on the system or even be inﬂuenced by

the used implementations. Hence, we evaluated the

visited states instead to study the relative effective-

ness of the different secondary tie-breakers. Tables 1

and 2 show the mean and median data, respectively.

Still, these numbers are close, and the question

remains whether any of these secondary tie-breakers

makes a real difference when the primary tie-breaker

is based on the h-values. Since the results could have

come from chance ﬂuctuation, we employed the sign

test again for investigating that. More precisely, we

tested a null hypothesis for each problem difﬁculty:

the median of the pair-wise differences between the

visited states of A* [h, LIFO], A* [h, VIATRA2] and

A* [h, FIFO] is 0, on a signiﬁcance level of .05, for

abs

(s) = 0, 1, 2. Since these null hypotheses cannot

be rejected, it seems as though secondary tie-breakers

do not really matter in our domain when the primary

tie-breaker is based on the h-values.

Overall, it seems clear that the answer to our RQ2

is no. That is, a LIFO tie-breaker is not generally bet-

ter in terms of A* search efﬁciency than a tie-breaker

using minimal heuristic values, as the recent results

in the literature suggest for non-zero-cost domains,

see (Asai and Fukunaga, 2017). At least in our do-

main and for unit-costs, it is most likely even worse.

6 RELATED WORK ON A*

TIE-BREAKING

Recently, there was increasing interest in tie-breaking

strategies for A*, but primarily for zero-cost domains.

(Asai and Fukunaga, 2016) discussed tie-breaking

strategies for zero-cost actions and showed that a

custom tie-breaking strategy can have signiﬁcant im-

pact on the search algorithm performance. (Asai and

Fukunaga, 2017) expanded on their previous results

and introduced two new classes of tie-breaking strate-

gies. They demonstrated that their approach signif-

icantly outperformed standard strategies on domains

with zero-cost actions. (Corrła et al., 2018) proposed

a tie-breaking strategy using cost adaptation that guar-

antees optimal expansion for zero-cost domains. In

contrast, our problems have unit costs for transforma-

tion steps (greater than zero), where these new ap-

proaches for zero-cost domains are not applicable.

For non-zero-cost domains, such as ours with unit-

costs, which A* was originally deﬁned for, there was

for a long time some rumor on how to tie-break most

effectively, but there were no really founded general

results. (Helmert, 2006) used a FIFO tie-breaking

Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space Exploration: A* Tie-breaking

601

Table 1: Mean numbers of visited states of A* searches using different tie-breaking strategies on problems with different

abs

(s).

[h, LIFO] [h, VIATRA2] [h, FIFO]

C* 0 1 2 0 1 2 0 1 2

7 131 2,676 6,043 210 2,603 6,024 177 2,665 6,156

8 110 7,001 12,159 107 7,138 12,065 120 7,058 12,132

9 603 12,267 22,968 947 12,668 22,529 854 12,640 22,918

10 4,526 46,506 95,242 2,911 47,084 95,625 4,528 47,209 94,927

Table 2: Median numbers of visited states of A* searches using different tie-breaking strategies on problems with different

abs

(s).

[h, LIFO] [h, VIATRA2] [h, FIFO]

C* 0 1 2 0 1 2 0 1 2

7 89 2,531 6,349 90 2,565 6,259 92 2,640 6,539

8 107 7,440 14,157 99 7,346 13,834 108 7,435 14,121

9 131 11,276 26,670 129 12,351 27,022 128 12,411 25,962

10 150 48,175 88,406 152 50,016 87,816 147 47,108 87,227

strategy in his A*-based planner named Fast Down-

ward. In contrast, (Hansen and Zhou, 2007) stated

that “It is well-known that A* achieves best perfor-

mance when it breaks ties in favor of nodes with least

h-cost”. (Holte, 2010) stated that “A* breaks ties in

favor of larger g-values, as is most often done”, and

this is equivalent to tie-breaking according to smallest

h-values. (R

oger and Helmert, 2010) also used small-

est h-values to break ties, and applied for still remain-

ing ties a FIFO tie-breaking policy as a second-level

criterion. Also (Burns et al., 2013) used smallest h-

values to break ties, but applied a LIFO tie-breaking

policy (instead of FIFO) as a second-level criterion.

Recently, (Asai and Fukunaga, 2017) reported

on experiments using the IPC Planning Competition

Benchmarks and concluded that breaking ties using

smallest h-values is not necessarily the best strat-

egy in such non-zero-cost domains, while simply us-

ing LIFO may even be better. This also depends,

however, on the second-level criterion used after tie-

breaking using smallest h-values. Their experiments

measured the number of problems solvable with given

resources, while our experiments compared node ex-

pansions and running times on problems that all the

compared variants solved (in the HSI domain). We

also investigated statistical signiﬁcance of the key re-

sults.

7 DISCUSSION

Interestingly, our results in our real-world domain as

shown above are more conformant to previous rumor

than to the results of (Asai and Fukunaga, 2017). Af-

ter all, our data indicate a statistically signiﬁcant su-

periority of using minimal h-values as a tie-breaker

(independently of using LIFO or FIFO as a secondary

tie-breaker) over directly using LIFO as a tie-breaker.

This is in contrast to Asai and Fukunaga’s statement

based on their experiments using IPC domains (Asai

and Fukunaga, 2017, p. 69):

“Tie-breaking according to the heuristic value

h, which is frequently mentioned in the heuris-

tic search literature, has little impact on the

performance as long as lifo default criterion

is used — in other words, a lifo tie-breaking

policy is sufﬁcient for most IPC domains.”

The fact that using minimal h-values was better

than LIFO as a tie-breaker in our experiments may be

the result of several contributing factors. First, our

problems have unit costs, and transformation steps

are only included into the search if they contribute to

achieving the given goal condition. Thus, while each

step costs one unit, it also gets one step closer to a goal

state, which reduces the h-value by one. Therefore,

the resulting nodes from this node expansion have

ICSOFT 2019 - 14th International Conference on Software Technologies

602

now the smallest h-value for the h-based tie-breaker.

Given that, secondary tie-breakers such as LIFO or

FIFO do not have much inﬂuence on the search per-

formance. In contrast, LIFO as a tie-breaker (without

consideration of h-values) implements a strict depth-

ﬁrst search among the nodes with the same f -values,

and it may not always lead to an optimal path towards

a goal node when starting it from a node with a greater

than minimal h-value. This is especially the case with

abs

> 0, where reconﬁguration is necessary.

8 CONCLUSION

Some real-world domains appear to have special

kinds of problems. In the case of HSIs, they show

a mix of trivial problems (without an actual need

for search) with problems including reconﬁguration

(which require search for ﬁnding optimal solutions).

While previous theoretical work indicated the need

for a tie-breaker of A* instead of random selection

from several nodes with the minimum value, we are

not aware of such dramatic differences that we have

observed through using different tie-breakers. They

appear to be due to the problems having unit costs

and that they are often — but not always — easy.

Summarizing, the contributions of this paper are

• A more theoretical treatment of deﬁning an ad-

missible heuristic in this HSI domain,

• A dramatic improvement over such HSI searches

with the default implementation of A* in the

VIATRA2 tool, especially for trivial problems,

• Deﬁnitions of metrics for measuring the difﬁculty

of problems,

• Analysis of statistical signiﬁcance for the cases

with relatively close results from different tie-

breakers, and

• New results and insights on tie-breaking using

minimum h-values vs. LIFO in a real-world do-

main with unit-costs.

Based on our results on h-based tie-breaking vs.

the recent results on LIFO-based tiebreaking by (Asai

and Fukunaga, 2017), and considering the diversity

of statements in the previous related work about such

tie-breakers, we conjecture that there is no generally

best tie-breaker for A* in non-zero-cost domains. It

seems as though this is domain-speciﬁc, and future

work should ﬁnd out the criteria for the preference of

one such tie-breaker over others.

ACKNOWLEDGEMENTS

We would like to thank Oszkar Semerath from the

VIATRA team for having pointed us to the place

in the implementation where the tie-breaker can be

changed.

The InteReUse project (No. 855399) is funded

by the Austrian Federal Ministry of Transport, In-

novation and Technology (BMVIT) under the pro-

gram “ICT of the Future” between September 2016

and August 2019. More information can be found at

https://iktderzukunft.at/en/.

REFERENCES

Asai, M. and Fukunaga, A. (2017). Tie-Breaking Strategies

for Cost-Optimal Best First Search. J. Artif. Intell.

Res., 58:67–121.

Asai, M. and Fukunaga, A. S. (2016). Tiebreaking Strate-

gies for A* Search: How to Explore the Final Fron-

tier. In Schuurmans, D. and Wellman, M. P., editors,

Proceedings of the Thirtieth AAAI Conference on Ar-

tiﬁcial Intelligence, February 12-17, 2016, Phoenix,

Arizona, USA., pages 673–679. AAAI Press.

Bergmann, G., D

avid, I., Heged

us,

A., Horv

ath,

A., R

ath, I.,

Ujhelyi, Z., and Varr

o, D. (2015). Viatra 3: A Reactive

Model Transformation Platform. In Kolovos, D. and

Wimmer, M., editors, Theory and Practice of Model

Transformations, pages 101–110, Cham. Springer In-

ternational Publishing.

Burns, E., Ruml, W., and Do, M. B. (2013). Heuris-

tic Search when Time Matters. J. Artif. Int. Res.,

47(1):697–740.

Corrła, A. B., Pereira, A. G., and Ritt, M. (2018). Analyz-

ing Tie-Breaking Strategies for the A* Algorithm. In

Proceedings of the Twenty-Seventh International Joint

Conference on Artiﬁcial Intelligence, IJCAI-18, pages

4715–4721. International Joint Conferences on Artiﬁ-

cial Intelligence Organization.

Dechter, R. and Pearl, J. (1985). Generalized best-

ﬁrst strategies and the optimality of A

∗

. J. ACM,

32(3):505–536.

Hansen, E. A. and Zhou, R. (2007). Anytime Heuristic

Search. J. Artif. Int. Res., 28(1):267–297.

Hart, P., Nilsson, N., and Raphael, B. (1968). A formal

basis for the heuristic determination of minimum cost

paths. IEEE Transactions on Systems Science and Cy-

bernetics (SSC), SSC-4(2):100–107.

Helmert, M. (2006). The Fast Downward Planning System.

J. Artif. Int. Res., 26(1):191–246.

Holte, R. C. (2010). Common Misconceptions Concerning

Heuristic Search. In Felner, A. and Sturtevant, N. R.,

editors, Proceedings of the Third Annual Symposium

on Combinatorial Search, SOCS 2010, Stone Moun-

tain, Atlanta, Georgia, USA, July 8-10, 2010. AAAI

Press.

Efﬁciently Finding Optimal Solutions to Easy Problems in Design Space Exploration: A* Tie-breaking

603

Kaindl, H. and Kainz, G. (1997). Bidirectional heuristic

search reconsidered. Journal of Artiﬁcial Intelligence

Research (JAIR), 7:283–317.

Kaindl, H., Kainz, G., Leeb, A., and Smetana, H. (1995).

How to use limited memory in heuristic search. In

Proc. Fourteenth International Joint Conference on

Artiﬁcial Intelligence (IJCAI-95), pages 236–242. San

Francisco, CA: Morgan Kaufmann Publishers.

Pearl, J. (1984). Heuristics: Intelligent Search Strate-

gies for Computer Problem Solving. Addison-Wesley,

Reading, MA.

Rathfux, T., Kaindl, H., Hoch, R., and Lukasch, F. (2019).

An Experimental Evaluation of Design Space Explo-

ration of Hardware/Software Interfaces. In Damiani,

E., Spanoudakis, G., and Maciaszek, L. A., editors,

Proceedings of the 14th International Conference on

Evaluation of Novel Approaches to Software Engi-

neering, ENASE 2019, Heraklion, Crete, Greece, May

4-5, 2019., pages 289–296. SciTePress.

oger, G. and Helmert, M. (2010). The More, the Mer-

rier: Combining Heuristic Estimators for Satisﬁcing

Planning. In Brafman, R. I., Geffner, H., Hoffmann,

J., and Kautz, H. A., editors, Proceedings of the 20th

International Conference on Automated Planning and

Scheduling, ICAPS 2010, Toronto, Ontario, Canada,

May 12-16, 2010, pages 246–249. AAAI.

ICSOFT 2019 - 14th International Conference on Software Technologies

604