
A Simulation Approach based Project Schedule Assessment
Ruiping Wang
1
a
, Xu Li
2
, Xiao Song
2 b
, Lei Dai
2
and Yixin Li
2
1
School of Electronic and Information Engineering, Beihang University, Beijing, China
2
State Key Laboratory of Intelligent Manufacturing System Technology, Beijing Institute of Electronic System Engineering,
Beijing, China
Keywords: Project Schedule, Simulation, Petri Net.
Abstract: Traditional program evaluation and review technique lacks of complex task relation models. To tackle this,
this paper proposes a project schedule risk assessment model based on extended Petri net, in which the
characteristics of task duration, task overlap and sub-tasks are modelled. Based on the characteristics of
concurrent iteration in product development schedule, the influence of each sub-task relationship on the
simulation uncertainty is considered. In this case, several mathematical distributions are used to simulate the
schedule of the subtask based on its own characteristics and the relationship between them. Based on the
above modelling, the key path of the project schedule is selected, and the transition mechanism of state
change in the simulation is designed. Finally, simulation results show that the proposed project schedule risk
assessment method can provide specific reference for the development plan of the whole project and its sub-
projects. In addition, the model can also be used to evaluate the cost of the project and establish the cost
standard of the project according to the evaluation.
a
https://orcid.org/0000-0001-6234-3007
b
https://orcid.org/0000-0003-4279-426X
1 INTRODUCTION
Along with the high-speed progress of science and
technology, complex product development has
greater project scale and more task types in civilian
and military applications. This makes the project
schedule risk assessment a challenging problem. In
most cases, the development schedule of complex
product can be divided into several independent sub-
systems, which often have complex constraints on
their finish-start relations. These task correlations
among subsystems increase the risk of product
development.
Traditional program evaluation and review
technique lacks of complex task relation modelling.
For instance, Tian (Tian et al., 2008) established the
project schedule risk model on the basis of multiple
risk attribute analysis. Meantime, the distribution
function of task progress assessment method is
given, and various risk factors for time delay were
summarized. But the start-finish relations of tasks
are not considered and evaluated. Huang (Huang et
al., 2005) tried to simulate and analyse the whole
project progress by establishing a random network
schedule model with Monta Carlo simulation. These
works are useful, but the resource constraint relation
between tasks is neglected. This might lead to its
project schedule inaccuracies.
To tackle this problem, we will design a petri net
based modelling method to describe project
schedules and evaluate its timespan.
The paper is structured as follows. Section 2 will
establish the formal descriptions of extended petri
net. In Section 3, detailed project model is given.
Section 4 presents the simulation process and
Section 5 gives a case study.
2 PROGRESS MODELING
BASED ON EXTENDED PETRI
NET
Petri net is the network structure information flow
model proposed by C.A.Petri in 1962 in his doctoral
dissertation for the first time (Browning and
Eppinger, 2002). The basic Petri net is defined as a
422
Wang, R., Li, X., Song, X., Dai, L. and Li, Y.
A Simulation Approach based Project Schedule Assessment.
DOI: 10.5220/0008124204220428
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 422-428
ISBN: 978-989-758-381-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
triple net; The extended Petri net (Mok et al., 2001)
defined in this paper is as follows:
(1)
The meanings of each symbol are as follows:
is finite set of places;
is a finite set of transition
nodes; . Also, P and T can’t be zero at the
same time. , F is the flow
relationship on the PN, and its elements are called
arcs. And
, among them
.
L is a hierarchical relation set of hierarchical
Petri nets. Each of these elements contains
information such as the level of the Petri net model
in which it is located and its parent level.
C is a set of colors in a colored Petri net,
corresponding to the resources in project
management (Fehling, 1991). The attributes of each
color include quantity, unit value in a certain period
of time, and other information.
Petri is the priority set of Petri net transitions.
The priority here does not play a role in the normal
transition. When the transition is deadlocked, it will
play a role in breaking the deadlock.
3 EXTENDED PETRI NET
SCHEDULE MODELING
3.1 Project Schedule Management and
High-level Petri Net Modeling
(1) Petri net modeling of task duration (Barad,
2016):
The duration of complex product development tasks
can’t be specifically determined during the
development of schedules. Therefore, this paper
assumes that the duration of the development of
complex products is subject to the distribution of
certain parameters or a certain value. Taking into
account the characteristics of time-delay Petri nets
and random networks, it will be used to describe the
task duration in project management.
(2) Petri net modeling of summary tasks:
In view of the close relationship between certain
tasks in the development of complex products and
the large number of tasks, these tasks are often
regarded as a task body. Another "virtual task" is
abstracted to contain the task body (Hussin, 1992).
Project managers only need to model abstract virtual
tasks (also known as summary tasks) in the first
level of task planning (Zaitsev and Shmeleva, 2011).
The detailed task information under this virtual task
can find the corresponding detailed task plan
diagram at the second level, and the hierarchical
relationship of this task can be extended down as
needed. In view of the close relationship between
certain tasks in the development of complex
products and the large number of tasks, these tasks
are often regarded as a task body. Another "virtual
task" is abstracted to contain the task body. Project
managers need to model only abstract virtual tasks,
also known as summary tasks, in the first level of
task planning. The detailed task information under
this virtual task can find the corresponding detailed
task plan diagram at the second level, and the
hierarchical relationship of this task can be extended
down as needed. Due to the hierarchical network in
the structure and the demand of project management
is very close, so this paper put the virtual task of the
project management corresponds to the node, task
relationship under virtual tasks correspond to a
hierarchical subnet.
(3) Petri net modeling of task overlapping relation:
In real project management, there is often a time-
constrained relationship among tasks (Rickert and
Schreckenberg, 2013). Generally, it is the lap
network plan: finish-start (FS), finish- finish (FF),
start- start (SS) and start-finish(SF). The four
overlapping relationships are defined as follows
(Neumann and Burks, 2012):
Table 1: Four task relation types.
A
B
FS type
A
B
FF type
A
B
SS type
A
B
SF type
1) FS type: This type indicates that the B task cannot
be started until the A task is completed.
2) FF type: It Indicates that B can only be finished
after A has been finished.
3) SS type. SS indicates that B can only start after A
task starts.
4) SF type. SF indicates that task B can only be
finished after task A starts.
A Simulation Approach based Project Schedule Assessment
423
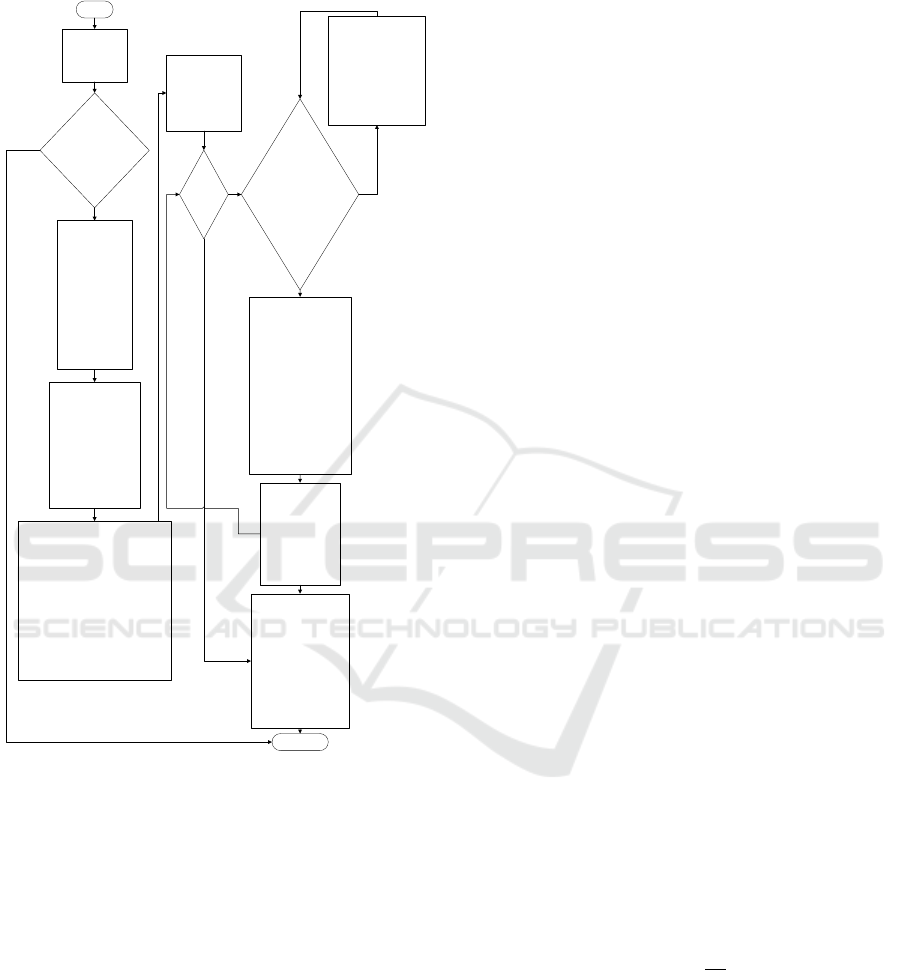
3.2 Project Progress Assessment
Method
Start
(1)Load
Project
xml file
(2)Whether
the xml file
format is
legal
(3)Store the
xml arc and
task
information
in link and
task table in
databases
respectively
(4)Increase the
resource
information
and save the
information to
resource and
resource_type
(5)Set priorities, duration
distribution functions and
their parameters,
restriction types, required
resources, etc. for each
task, and save the
information to task,
task_resource, and its
math_expression_arg
(6)Enter the
number of
simulations
N, let i=1
(7)
i N
(8)Examine
Whether
the currently
activated task
has a
deadlock
(10)Tasks
satisfiedresource
constraints
continue to be
simulated
according to
constraints and
overlap rules
until the end of
the simulation.
(11)Save the
data related
to the above
task
simulation
results, i=i+1
(12)At the
end of N
simulations, the
simulation
results were
processed,
counted and
reported
(9)Execute the
multi-task
competing
resource
deadlock
algorithm
(13)End
Y
Y Y
N
N
N
Figure 1: Project progress simulation flow.
(1) Load the project task relationship and structure
diagram files into memory;
(2) Check whether the task relationship and
attributes of the XML file are legal (including
whether or not there is a deadlock check caused by
the task associative relationship). If step 3 is
performed legally, go to step 2.
(3) Parse the arc information,task information and
other informations in the XML file, and store them
in the database link table, task table and other related
tables in the background. Then perform the step 4.
(4) In the resource management interface, the
number of resources required for the task, resource
type, and other information are added, and saved in
the resource tables and the resource type tables.
Then go to step 5.
(5) Setting the priority of task, the distribution
function types, parameters of the time limit and
other related information for a project in the task
management interface, and save to the task table,
task_resource table, math_expression_type table and
so on. Perform step 6.
(6) Input the times of simulation, and set i =1.
Perform step 7.
(7) Judge i≤N, if the condition is true, execute step 8,
or else execute step 11.
(8) Check whether the currently active task set S has
a deadlock due to resources. If it exists, execute the
"multitasking competitive resource deadlock"
algorithm (while saving related information to the
database), and perform step 9.
(9) Execute "transition node state transition"
algorithm for activated tasks.
(10) Save the relevant data of the above simulation
results, let i=i+1; go to step 7.
(11) When simulation is completed, the simulation
results are processed, counted, and reported. Perform
step 12.
(12) End of simulation.
The above process is shown in figure 1.
4 PROGRESS RISK ANALYSIS
BASED ON SIMULATION
RESULTS
In order to calculate the probability of schedule risk
in the development of complex products, the
correlation of schedule risk is now analyzed as
follows (Song and Gong, 2015):
Considering the simulation is run N times, the
simulation result shows that the production cycle p
is repeated np times (Song et al., 2018). Then the
probability of occurrence of the project duration P
(D = p) (Ma et al., 2016) is:
(2)
The risk probability P(D ≠ p) of the project's
simulation duration is not p (Song et al., 2013):
(3)
In the N simulations, the simulation result set with
the simulation duration less than or equal to p is {p
1
,
p
2
, ..., p
r
}, and the frequency set of the
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
424
corresponding simulation result is {c
1
, c
2
, ..., c
r
}, and
, so the project duration is less than or
equal to p of the probability (Shi et al., 2015) is:
(4)
The probability that the project duration is
greater than p is:
(5)
The risk probability of the project duration
between [p
a
, p
b
) (Song et al., 2010) is
:
(6)
According to the specific shape of the project
period (frequency) scatter plot obtained by N
simulations, the law of the scatter plots is searched,
and the cumulative probability distribution function
relationship of the complex product development
period can be obtained by using curve fitting, and
the hypothesis is F(x) (Suhariyanto et al., 2017). x is
the simulation period, then the corresponding
product development schedule risk probability
distribution function F
f
(x) is:
(7)
Based on the schedule risk probability
distribution function, the risk trend can be seen
intuitively, and the schedule risk duration of the
complex product development period being less than
a certain period of time or a certain period of time
interval can be calculated, thereby verifying the
designated project progress for the project manager.
The rationality of the plan provides the basis and
also provides a reference for the further decision-
making of the project schedule (Luz and Francisco,
2018).
5 SIMULATION AND ANALYSIS
OF CASE RESULTS
There are a total of 30 tasks in the selected project,
including six summary tasks. The remaining 24 task
durations are described below:
Table 2: Project task duration information. Task duration
is often stochastic in practice. Here we use triangular and
normal distribution to describe it.
ID
Task name
Task
duration
distribution
Task paras
Estimated
duration of
task (day)
2
The design of
the product
Triangular
distribution
(30,45,60)
45
3
Product
documentation
preparation
Triangular
distribution
(41,45,61)
49
4
Material
preparation
Triangular
distribution
(23,36,43)
33
5
Finalizing of
gland
Normal
distribution
(37,2)
37
7
Gland curing
Normal
distribution
(41,3)
41
8
Gland polishing
Normal
distribution
(43,2)
43
9
The setting and
curing of filter
Normal
distribution
(43,4)
43
10
Clean the
gland surface
Normal
distribution
(39,1)
39
11
Gland assembly
Normal
distribution
(37,2)
37
13
Welding ring
test assembly
Triangular
distribution
(90,100,140)
110
12
Welding
ring curing
Triangular
distribution
(110,130,150)
130
15
Skeleton test
and protection
Normal
distribution
(37,2)
37
17
Skeleton shell
blowing sand
Normal
distribution
(30,2)
30
18
Skeleton shell
set, curing
Normal
distribution
(38,4)
38
19
Skeleton
detection
Normal
distribution
(33,3)
33
20
End face of
skeleton shell
Normal
distribution
(36,2)
36
21
Skeleton
punching
Normal
distribution
(33,1)
33
22
Skeleton
shell paint
Normal
distribution
(34,3)
34
23
Pilot cone
production
Normal
distribution
(41,4)
41
25
Outlet nozzle
Normal
distribution
(37,2)
37
26
Filter assembly
Triangular
distribution
(44,56,62)
54
27
Filter test
Triangular
distribution
(35,45,52)
44
29
Physical accep-
tance of filter
Triangular
distribution
(24,46,50)
40
30
The Acceptance
review of filter
Triangular
distribution
(25,45,53)
41
Throughout the investigation of the real-world
data in this community, we find the relevant
parameters of the auto vehicle driving behavior at
the intersection of the cell structure, as shown in the
following figure. These data are our model input
parameters.
A Simulation Approach based Project Schedule Assessment
425
The following figure shows the relationship
diagram of 30 tasks. A round-cornered box
represents a task body. The virtual circle in the task
represents a summary task id. Due to the
complicated lapped relationship, no detailed
description is given here.
10
15
17
9
75
8
1918
11
21 20
16
22
1
2 3
4
12
14
13
2523 26
27
24
28 30
29
6
Figure 2: Mapping of product structure and development
project.
For FS type, it is widely used in practice. After
the previous task is finished generating specific
resource, the latter task can then begin.
Tasks 11 and 15 are FF type. Task 15 restricts
the completion time of Task 11. Task 11 can be
completed after Task 15 is completed.
Task 7 and Task 8 are SF type, which requires
Task 7 to be completed after Task8 begins. Since
Task 8 lasts longer than Task 7, Task 8 can be
divided into two subtasks named Task8.1 and
Task8.2, Task 8.1 has the same time limit with Task
7, and the remaining time is used to complete the
task 8.2. This task type can be transformed into FF
type. that is, when task 8.1 is completed, task 7 can
also be completed.
We can calculate the critical path from figure2:
According to the above analysis, the total
planned duration of Task 8 and Task 7 is 43 days,
and the planned duration of Task 11 and Task 15 is
39 days.
Path 1 (including task 5/7/8/9/10), the expected
completion time of the task is: 162 days.
Path 2 (including task 12/13), the expected
completion time of the task is: 240 days.
Path 3 (including task 11/15/17/18/19/20/21/22),
the expected completion time of the task is: 243 days
By analyzing the total duration of the three paths
above, the critical path of the project can be drawn
as:
Figure 3: The critical path of the project.
According to the calculation, the construction
period of the critical path of the project is 625 days.
Figure 4 shows the statistics of the number of
times each task becomes a critical task within 2000
simulations, so it can be more intuitive to see which
tasks have a greater impact on the whole
construction period. And we can determine the
critical path in Figure 5 from this figure.
Figure 4: Simulation results of critical tasks’ frequencies
within 2000 simulation.
Horizontal axis is the sequence number of the
task. Vertical axis is the number of a task observed
to be a critical task.
Figure 5: Average duration of the subtask simulation.
The figure 5 shows the average duration of each
subtask with 3000 simulations. It can be seen that
the task duration is very close to the expected value.
The figure 6 shows the frequency diagram of the
simulation period. It can be seen from the figure that
the distribution of the duration of the task presents a
middle concentration and the two ends gradually
decrease.
Figure 6: Frequency distribution of project duration.
2 3 4 15 1817 20 21 2219 23
2526272830
0
500
1000
1500
2000
2500
2 4 7 9 11 13 17 19 21 23 26 28
Frequency of key
tasks(d)
Task(ID)
0
50
100
150
200
2 3 4 5 7 8 9 10 11 12 13 15 17 18 19 20 21 22 23 25 26 27 28 30
Task time (d)
Task(ID)
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
426
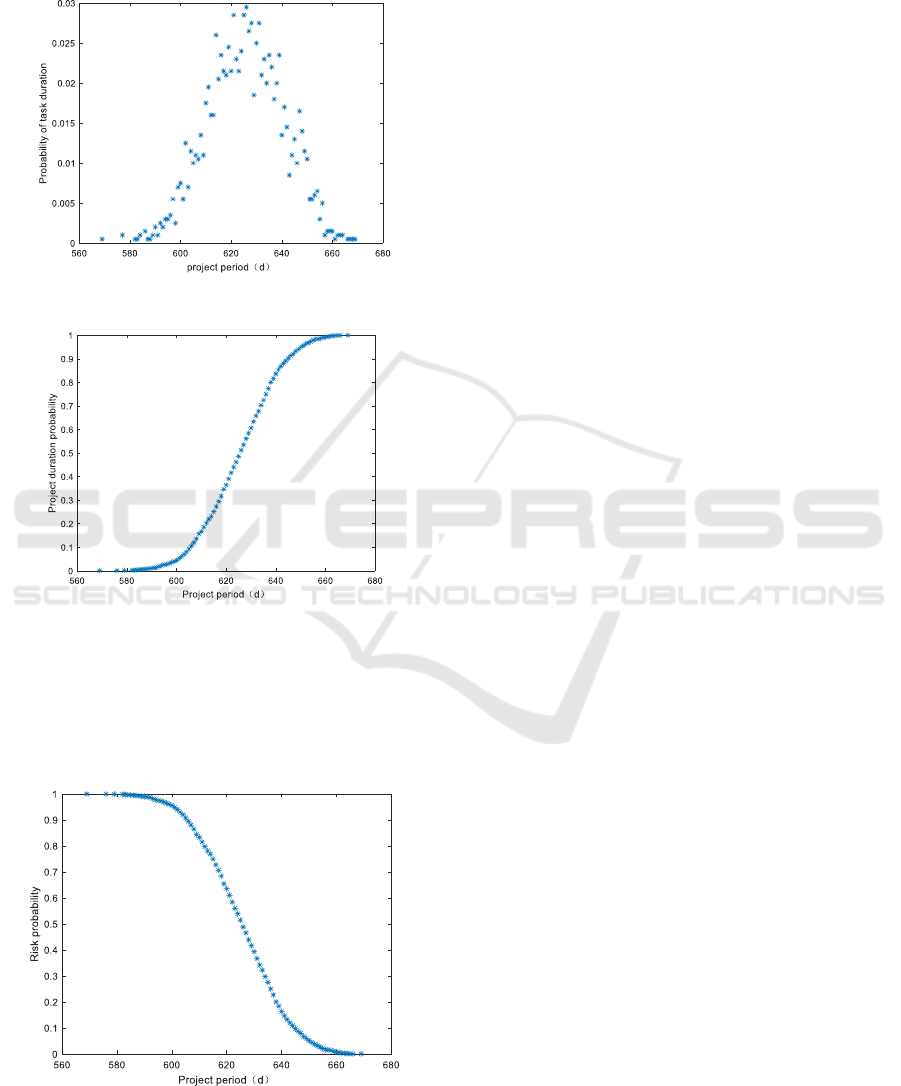
Figure 7 shows the probability of the project
construction period simulation. We can see that it is
most appropriate to set the project construction
period at around 620 days.
Figure 7: Probability distribution of project duration.
Figure 8: Probability of project duration cumulative.
Figure 8 shows the project simulation duration
accumulation probability. It can be concluded that
the maximum duration of the project development is
about 660 days, and the probability of the project
period is less than 640 days is more than 80%.
Figure 9: Project duration risk probability.
As can be seen from Figure 9, when the project
duration is set within 580 days, the project can’t be
completed on time.
6 CONCLUSIONS
A schedule risk assessment method based on
extended Petri nets is proposed. Based on the high-
level Petri nets (layered Petri nets, stochastic Petri
nets, colored Petri nets), Petri nets are modeled for
the task duration, mission affiliation, and task
restriction types in project management, which
extends Petri nets' changes. At the same time, the
scheduling simulation algorithm based on extended
Petri net is proposed. Based on the analysis of the
simulation results, a method for estimating the
progress risk of the development of complex
products is presented.
REFERENCES
Xinguang Tian, Zhiming Qiu etc. An Analysis of Progress
Risk of Naval Gun Weapons Development Based on
Multiple Risk Probability Model. Acta Armamentarii,
2008.5, 29(5): 521-525.
Zhaodong Huang, Yiyong Xiao etc. Schedule Risk
Random Network Modeling and Simulation Analysis.
Journal of Academy of Armored Force Engineering
2005.3, 19(1): 48-50.
Tyson R. Browning, Steven D. Eppinger. B Modeling
Impacts of Process Architecture on Cost and Schedule
Risk in Product Development. IEEE Transaction on
Engineering Management, (S0018-9391), 2002, 49(4):
428-442.
Mok C K, Chin K, Ho K L. An interactive knowledge-
based CAD system for mould design in injection
moulding processes. The International Journal of
Advanced Manufacturing Technology. 2001, 17(1)-45:
27-28.
Ralner Fehling. A concept of Hierarchical Petri Nets with
Building Blocks. The 12
th
International Conference on
Application and Theory of Petri Nets, 1991, 6, 370-
389.
Barad, M. Petri Nets-A Versatile Modeling Structure.
Applied Mathematics, 2016, 7, 829-839.
Abdul-Hussin, M.H. Elementary Siphons of Petri Nets and
Deadlock Control in FMS. Journal of Computer and
Communications, 1992, 3, 1-12.
Dmitry A, Zaitsev, Tatiana R. Shmeleva. A Parametric
Colored Petri Net Model of a Switched Network.
Network and System Sciences, 2011, 4, 65-76.
M. Rickert, K. Nagel, M. Schreckenberg, A. Latour.
Interrelation of Languages of Colored Petri Nets and
Some Traditional Languages. Open Journal of
Modelling and Simulation, 2013, 1, 27-29.
A Simulation Approach based Project Schedule Assessment
427

Von Neumann, J. and A. W. Burks. Modeling and
Simulation of Textile Supply Chain through Colored
Petri Nets. Intelligent Information Management, 2012,
4, 261-268.
Wu, Y, Song, X, Gong, G. Real-time load balancing
scheduling algorithm for periodic simulation models.
Simulation Modelling Practice and Theory, 2015,
52(1): 123-134.
X. Song, D. Han, J. Sun, Z. Zhang. A data-driven neural
network approach to simulate pedestrian movement.
Physica A-statistical mechanics and its applications,
2018, 509(11): 827-844.
L. Ma, X. Song, Y. Ma, et al. Selfishness- and
Selflessness-based Models of Pedestrian Room
Evacuation. Physica A-statistical mechanics and its
applications, 2016, 447(4): 455–466.
X. Song, Shaoyun Zhang, Lidong Qian. Opinion dynamics
in networked command and control organizations.
Physical A - statistical mechanics and its applications,
2013, 392(20): 5206-5217.
Wen Shi, X. Song, Yaofei Ma, Chen Yang. Impact of
Informal Networks on Opinion Dynamics in
Hierarchically Formal Organization. Physica A-
statistical mechanics and its applications, 2015,
436(10): 916-924.
Song, X, Chai, X, Zhang, L. Modeling Framework for
Product Lifecycle Information. Simulation Modelling
Practice and Theory, 2010, 18(8): 1080-1091.
Suhariyanto T T, Wahab D A, Rahman M N, et al. Multi-
Life Cycle Assessment for sustainable products. A
systematic review, Journal of Cleaner Production,
2017, 677-696.
Leila Mendes da Luz, Antonio Carlos de Francisco.
Integrating life cycle assessment in the product
development process. A methodological approach,
Journal of Cleaner Production, Journal of Cleaner
Production, 2018, 193, 28-42.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
428
