Algorithm and Software to Generate Code for
Wendland Functions in Factorized Form
Hjortur Bjornsson and Sigurdur Hafstein
a
Science Institute, University of Iceland, Dunhagi 3, 107 Reykjav
´
ık, Iceland
Keywords: Wendland Function, Lyapunov Functions, Radial Basis Functions, Code Generation.
Abstract:
In this paper we describe an algorithm to determine Wendland’s Radial Basis Functions in a specific factorized
form. Additionally, we present a software tool that uses this algorithm to generate a C/C++ library that
implements the Wendland functions with arbitrary parameters in factorized form. This library is more efficient
and has higher numerical accuracy than previous implementations. The software tool is written in Python and
is available for download.
1 INTRODUCTION
Interpolation and collocation using Radial Basis
Functions (RBF), in particular compactly supported
RBFs, has been the subject of numerous research
activities in the past decades (Wu, 1992; Floater
and Iske, 1996; Franke and Schaback, 1998; Wend-
land, 1998; Buhmann, 2003; Buhmann, 2000; Wend-
land, 2005; Wendland, 2017). They are well suited
as kernels of Reproducing Kernel Hilbert Spaces
and their mathematical theory is mature. The au-
thors and their collaborators have applied Wend-
land’s compactly supported RBFs for computing Lya-
punov functions for nonlinear systems, both deter-
ministic (Giesl, 2007; Giesl, 2008; Giesl and Haf-
stein, 2015) and stochastic (Bjornsson et al., 2019).
Lyapunov functions are a useful tool to analyse sta-
bility of various dynamical systems, either determin-
istic or stochastic, cf. e.g. (Khalil, 2002; Sastry, 1999;
Vidyasagar, 2002; Khasminskii, 2012; Mao, 2008).
Various numerical methods have been used to find
Lyapunov functions for the systems at hand (Giesl and
Hafstein, 2015; Hafstein et al., 2018). Meshless col-
location using RBFs is one such method and many
different families of RBFs have been studied (Wend-
land, 2005).
In the papers (Giesl and Hafstein, 2015; Bjorns-
son et al., 2019) meshless collocation with so called
Wendland functions is used. The Wendland functions
are compactly supported radial functions, that are
polynomials on their support. The Wendland function
a
https://orcid.org/0000-0003-0073-2765
family is defined in such a way that many tedious and
error prone calculations have to be done by hand in or-
der to obtain formulas for the functions to be used in
the software implementation in (Giesl and Hafstein,
2015; Bjornsson et al., 2019). In (Argaez et al., 2017)
an algorithm is proposed that determines the Wend-
land polynomials in expanded form, that is: for each
integer l,k ≥ 0 finds a list of numbers a
0
,a
1
,...a
d
such that the Wendland function ψ
l,k
(r) =
∑
d
i=0
a
i
r
i
on its compact support. However, it was shown in
(Bjornsson and Hafstein, 2018) that the evaluations of
these polynomials in this form using typical schemes,
such as Horner’s scheme, can lead to significant nu-
merical errors.
Evaluating the Wendland functions in factorized
form (Bjornsson and Hafstein, 2018) is more effi-
cient and numerically accurate, so we propose an al-
ternate algorithm to determine the functions in factor-
ized form. In addition to developing the algorithm,
we implemented it and created a software tool that
generates a reusable software library, which imple-
ments these Wendland polynomials in factorized form
in C/C++.
2 BACKGROUND
In the paper (Bjornsson et al., 2019), meshless collo-
cation using RBFs was used to calculate Lyapunov
functions for various Stochastic Differential Equa-
tions (SDE). This included computing, for a given do-
main Ω ⊂ R
n
and a boundary Γ ⊂ R
d
, a solution to the
Partial Differential Equation (PDE)
156
Bjornsson, H. and Hafstein, S.
Algorithm and Software to Generate Code for Wendland Functions in Factorized Form.
DOI: 10.5220/0008191901560162
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 156-162
ISBN: 978-989-758-380-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(
LV (x) = h(x) x ∈ Ω
V (x) = c(x) x ∈ Γ,
(1)
where L is a certain second-order differential op-
erator, and h and c are appropriately chosen functions.
A numerical solution to the above problem was deter-
mined by choosing points X
1
= {x
1
,...,x
N
} ⊂ Ω and
X
2
= {ξ
1
,...,ξ
M
} ⊂ Γ and solving the interpolation
problem
(
LV (x
i
) = h(x
i
) for all i = 1,...,N
V (ξ
i
) = c(ξ
i
) for all i = 1,...,M.
The solution to this interpolation problem is given by
V (x) =
N
∑
k=1
α
k
(δ
x
k
◦ L)
y
ψ(kx − yk)
+
M
∑
k=1
α
N+k
(δ
ξ
k
◦ L
0
)
y
ψ(kx − yk), (2)
where δ
y
V (x) = V (y), the superscript y denotes that
the operator is applied with respect to the variably y,
and the operator L
0
is the identity operator. Here the
function ψ is a compactly supported RBF (Wendland,
2017). The constants α
i
are determined as a solution
to the linear system Aα = γ, where A is the symmetric
and positive definite matrix
A =

B C
C
T
D

and the matrices B = (b
jk
)
j,k=1,...,N
, C =
(c
jk
)
j=1,...,N,k=1,...,M
and D = (d
jk
)
j,k=1,...,M
have
elements:
b
jk
= (δ
x
j
◦ L)
x
(δ
x
k
◦ L)
y
ψ(x − y)
c
jk
= (δ
x
j
◦ L)
x
(δ
ξ
k
◦ L
0
)
y
ψ(x − y)
d
jk
= (δ
ξ
j
◦ L
0
)
x
(δ
ξ
k
◦ L
0
)
y
ψ(x − y).
To compute such a Lyapunov function a large num-
ber of evaluations of the function ψ and its derivatives
is necessary. To verify the properties of a Lyapunov
function for the function computed, even more eval-
uations are necessary. Therefore, it turned out to be
essential that these evaluations could be carried out in
an efficient and accurate way.
3 WENDLAND FUNCTIONS
The Wendland functions are a family of functions, de-
pending on two parameters l,k ∈ N
0
defined by
ψ
l,0
(r) = [(1 − r)
+
]
l
(3)
and
ψ
l,k+1
(r) = C
l,k+1
Z
1
r
tψ
l,k
(t)dt, (4)
where (1 − r)
+
:= max{1 − r,0} and C
l,k+1
6= 0 is a
constant. For interpolation and collocation using a
particular Wendland function, the value of the con-
stant C
l,k+1
6= 0 is not of importance because the
Wendland function appears linearly on both sides of a
linear equation. Therefore, one can just fix values that
are convenient for the problem at hand and we will do
this in the following section. These functions satisfy
the relation
−C
l,k+1
ψ
l,k
(r) =
d
dr
ψ
l,k+1
(r)
r
. (5)
It is not difficult to verify that the functions
Φ
l,0
(r) = [(1 − r)
+
]
l
and (6)
Φ
l,k
(r) =
Z
1
r
Φ
l,0
(t)t(t
2
− r
2
)
k−1
dt for k > 0 (7)
also satisfy a relation of the form
−2(k − 1)Φ
l,k
(r) =
d
dr
Φ
l,k+1
(r)
r
,
for all integers k,l ≥ 0, i.e. a relation identical to equa-
tion (5) with C
l,k+1
= 2(k − 1). Just note that
d
dr
Z
1
r
Φ
l,0
(t)t(t
2
− r
2
)
k−1
dt
= −2r(k − 1)
Z
1
r
Φ
l,0
(t)t(t
2
− r
2
)
k−2
dt.
Therefore (7) delivers an alternative way to de-
fine the Wendland functions, see (Wendland, 2017).
Note that (Wendland, 2017) uses a different number-
ing scheme of the functions than we do.
The Wendland functions have several important
properties, cf. e.g. (Giesl, 2007, Prop. 3.10):
1. ψ
l,k
(r) is a polynomial of degree l + 2k for r ∈
[0,1] and supp(ψ
l,k
) = [0,1].
2. The radial function Ψ(x) := ψ
l,k
(kxk) is C
2k
at 0.
3. ψ
l,k
is C
k+l−1
at 1.
Frequently we fix the parameter l :=

n
2

+ k + 1,
where n is the space dimension we are working in, and
a constant c > 0 to fix the support. By the properties
stated above, the radial function Ψ(x) := ψ
l,k
(ckxk)
is then a C
2k
function with supp(Ψ) = B
d
(0,c
−1
) ⊂
R
n
, where B
n
(0,c
−1
) is the closed n-dimensional ball
around the origin with radius c
−1
.
Algorithm and Software to Generate Code for Wendland Functions in Factorized Form
157

4 ALGORITHM
We represent d-degree polynomials
∑
d
i=0
a
i
t
i
as a list
of coefficients (a
0
,a
1
,...,a
d
). Our implementation
uses Python with List objects. Addition and multipli-
cation of polynomials of this form are easily imple-
mented as:
d
1
∑
i=0
a
i
t
i
+
d
2
∑
j=0
b
j
t
j
=
max{d
1
,d
2
}
∑
i=0
(a
i
+ b
i
)t
i
,
where a
i
= 0 for i > d
1
and b
j
= 0 for j > d
2
. Multi-
plication is given by
d
1
∑
i=0
a
i
t
i
!
d
2
∑
j=0
b
j
t
j
!
=
d
1
+d
2
∑
i=0
c
i
t
i
,
where
c
i
=
∑
k+ j=i
a
k
b
j
.
An antiderivative of a polynomial is given by
(a
0
,a
1
,a
2
,...,a
d
) 7→ (0,a
0
,
a
1
2
,
a
2
3
,...,
a
d
d + 1
),
corresponding to
Z
d
∑
i=0
a
i
t
i
dt =
d
∑
i=0
a
i
i + 1
t
i+1
,
and differentiation by
(a
0
,a
1
,...,a
d
) 7→ (a
1
,2a
2
,3a
3
,...,da
d
).
In order to maximize exact calculations up to com-
puter limitations, we store the coefficients as tuples
of Integers, numerator and denominator, avoiding the
floating point approximation. Specifically, we used
the Rational class provided in Python. We can repre-
sent polynomials in two variables as a polynomial in
the first variable where each coefficient is a polyno-
mial in the second variable (of which each coefficient
is a rational number).
4.1 Construction
To calculate a polynomial representing the Wendland
function ψ
l,k
on the interval [0,1] we start by fixing
the derivative
p
0
(t) = (1 −t)
l
t(t
2
− r
2
)
k−1
,
see (7), which we represent as a polynomial in t with
each coefficient a polynomial in r. We integrate with
respect to t and obtain a new polynomial p(t) in t,
again with coefficients that are polynomials in r. We
evaluate the polynomial p at t = 1 and at t = r, which
in both cases result in a polynomial in r, and we obtain
the polynomial ψ(r) = p(1) − p(r). Note that ψ(r) =
C
1
ψ
l,k
(r) for some constant C
1
6= 0.
By using a long division algorithm we factor ψ
into the form
ψ(r) = C
2
(1 − r)
l+k
p
l,k
(r) (8)
such that p
l,k
(r) is a polynomial with integer coeffi-
cients with no common factors. This is possible since
ψ
l,0
has a zero of order l at 1, and by using the recur-
sive relation in equation (4), we see that ψ
l,k
has a zero
of order l + k at 1. Since ψ
l,k
is essentially only de-
fined up to a multiplicative non-zero constant, we dis-
card the constant C
2
and use ψ(r) = (1 − r)
l+k
p
l,k
(r),
a polynomial with integer coefficients, as a starting
point for our recursion.
Using the relation in (5), ignoring the constant
C
l,k
, we see that
ψ
l,k−1
(r) =
d
dr

(1 − r)
l+k
p
l,k
(r)

r
(9)
=
1
r
(1 − r)
l+k−1
((1 − r)p
0
l,k
(r) − (l + k)p
l,k
(r)).
Therefore we have
p
l,k−1
(r) :=
ψ
l,k−1
(r)
(1 − r)
l+k−1
(10)
=
1
r

(1 − r)p
0
l,k
(r) − (l + k)p
l,k
(r)

.
We know that ψ
l,k−1
is a polynomial, therefore
d
dr

(1 − r)
l+k
p
l,k
(r)

must by divisible by the mono-
mial r. Since (1 − r)
l+k−1
is not divisible by r, the
right-hand side of (10) must be a polynomial in r.
Therefore p
l,k−1
is a well defined polynomial.
By pulling out the common factor b
k−1
∈ Z of
the coefficients in p
l,k−1
we obtain a new polynomial
ˆp
l,k−1
and a constant b
k−1
such that
p
l,k−1
= b
k−1
ˆp
l,k−1
.
Repeating this step, until we arrive at p
l,0
, we get a
collection of polynomials in the form
ψ
i
(r) = b
1
···b
i
(1 − r)
l+k−i
ˆp
l,k−i
(r), i = 1, 2, . . . , k
(11)
where each of the polynomials ˆp
l,k−i
(r) has integer
coefficients and each of the constants b
i
is a negative
integer.
The above list follows the notation in (Giesl,
2007) were ψ
0
is the polynomial given in (8) and is
equal to the Wendland function ψ
l,k
, and ψ
1
,...,ψ
i
are the Wendland functions given by ψ
l,k−1
,...,ψ
l,k−i
respectively, see equation (4). It is important to keep
track of the constants b
1
,...,b
i
in (11) as they are nec-
essary for correct evaluation of formula (2).
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
158

4.2 Example
To see how the algorithm works let us consider how
it computes the Wendland function ψ
l,k
for l = 5 and
k = 4. Here p
0
(t) = (1 −t)
5
t(t
2
− r
2
)
3
and we obtain
ψ(r) =
Z
1
r
(1 −t)
5+4
t(t
2
− r
2
)
3
dt
= −
16
3003
r
13
+
1
24
r
12
−
32
231
r
11
+
1
4
r
10
−
16
63
r
9
+
1
8
r
8
−
1
42
r
6
+
1
168
r
4
−
1
924
r
2
+
1
10296
=
1
72072
(1 − r)
9
(384r
4
+ 453r
3
+ 237r
2
+ 63r + 7)
and set ψ
0
(r) = (1 − r)
9
(384r
4
+ 453r
3
+ 237r
2
+
63r + 7). For r ∈ [0,1] we have the formulas (recall
that ψ
l,k
(r) = 0 if r /∈ [0,1]):
ψ
5,4
(r) = ψ
0
(r)
= (1 − r)
9
(384r
4
+ 453r
3
+ 237r
2
+ 63r + 7)
ψ
5,3
(r) = ψ
1
(r) =
d
dr
ψ
0
(r)
r
= −156(1 − r)
8
(32r
3
+ 25r
2
+ 8r + 1)
ψ
5,2
(r) = ψ
2
(r) =
d
dr
ψ
1
(r)
r
= 3,432(1 − r)
7
(16r
2
+ 7r + 1)
ψ
5,1
(r) = ψ
3
(r) =
d
dr
ψ
2
(r)
r
= −82,368(1 − r)
6
(6r + 1)
ψ
5,0
(r) = ψ
4
(r) =
d
dr
ψ
3
(r)
r
= 3,459,456(1 − r)
5
Note that we have, indeed, computed a lot more useful
information than just a family of Wendland functions
ψ
5,i
, i = 0,1,...,4. In our algorithm, for a fixed l,k,
we have
ψ
l,k− j
= ψ
j
(r) =
d
dr
ψ
j−1
(r)
r
=
d
dr
ψ
l,k− j+1
(r)
r
, for j = 1,...,k,
and we have thus delivered all the radial basis func-
tions needed for a collocation problem. This corre-
sponds to computing a whole table as in (Giesl, 2007,
Table 3.1), but for a collocation problem with arbi-
trary high derivatives. In the software tool, discussed
in the next section, also the constant c > 0 used to fix
the support of the Wendland function, is included in
these computations.
5 SOFTWARE LIBRARY
We have implemented the above algorithm in a soft-
ware tool
1
that generates C/C++ code versions of the
Wendland functions in factorized form. In a previous
work (Bjornsson and Hafstein, 2018), we determined
that the most efficient and accurate way to evaluate
these Wendland functions was to use this factorized
form. Evaluating these polynomials in fully expanded
format using Horner’s scheme (Burrus et al., 2003),
can lead to very large numerical errors as shown in
(Bjornsson and Hafstein, 2018). Below is a part of the
library generated by our tool, which shows the family
of Wendland functions obtained when starting with
Ψ
0
(x) = ψ
5,4
(ckxk), where c > 0 is the constant that
controls the support of the radial function Ψ.
Listing 1: Generated code for the ψ
5,4
family.
1 d oub l e w e n d l a n d p s i 5 4 0 ( d oub l e x , ...
d oub l e c ) {
2 d oub l e t = i p ow ( ( 1 . 0 - x ) , 9 ) ;
3 t =1 . 0
*
t
*
( ( ( ( ( 3 8 4 )
*
x + 4 5 3 )
*
x + ...
23 7 )
*
x + 6 3 )
*
x + 7 ) ;
4 r e t u r n t ;
5 }
6 d o u b l e w e n d l a n d p s i 5 4 1 ( d o u b l e x , ...
d o u b l e c ) {
7 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 8 ) ;
8 t = - 156 . 0
*
t
*
i p o w ( c , 2 )
*
( ( ( ( 3 2 )
*
x ...
+ 2 5 )
*
x + 8 )
*
x + 1 ) ;
9 r e t u r n t ;
10 }
11 d o u b l e w e n d l a n d p s i 5 4 2 ( d o u b l e x , ...
d o u b l e c ) {
12 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 7 ) ;
13 t =3432 . 0
*
t
*
i p o w ( c , 4 )
*
( ( ( 1 6 )
*
x ...
+ 7 )
*
x + 1 ) ;
14 r e t u r n t ;
15 }
16 d o u b l e w e n d l a n d p s i 5 4 3 ( d o u b l e x , ...
d o u b l e c ) {
17 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 6 ) ;
18 t = -82 368 . 0
*
t
*
i p o w ( c , 6 )
*
( ( 6 )
*
x ...
+ 1 ) ;
19 r e t u r n t ;
20 }
21 d o u b l e w e n d l a n d p s i 5 4 4 ( d o u b l e x , ...
d o u b l e c ) {
22 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 5 ) ;
23 t =3459456 . 0
*
t
*
i p o w ( c , 8 )
*
( 1 ) ;
24 r e t u r n t ;
25 }
Note that wendlandpsi 5 4 j corresponds to
ψ
j
in the example, but with x = cr as argument.
When starting with Ψ
0
(x) = ψ
5,3
(ckxk) instead,
the relevant definitions are:
1
The tool is available at https://gitlab.com/hjortur/
wendland-function-generator/ with example outputs.
Algorithm and Software to Generate Code for Wendland Functions in Factorized Form
159

Listing 2: Generated code for the ψ
5,3
family.
1 d o u b l e w e n d l a n d p s i 5 3 0 ( d o u b l e ...
x , d o u b l e c ) {
2 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 8 ) ;
3 t =1 . 0
*
t
*
( ( ( ( 3 2 )
*
x + 2 5 )
*
x + ...
8 )
*
x + 1 ) ;
4 r e t u r n t ;
5 }
6 d o u b l e w e n d l a n d p s i 5 3 1 ( d o u b l e ...
x , d o u b l e c ) {
7 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 7 ) ;
8 t = -22 . 0
*
t
*
i p o w ( c , 2 )
*
( ( ( 1 6 )
*
x ...
+ 7 )
*
x + 1 ) ;
9 r e t u r n t ;
10 }
11 d o u b l e w e n d l a n d p s i 5 3 2 ( d o u b l e ...
x , d o u b l e c ) {
12 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 6 ) ;
13 t =528 . 0
*
t
*
i p o w ( c , 4 )
*
( ( 6 )
*
x ...
+ 1 ) ;
14 r e t u r n t ;
15 }
16 d o u b l e w e n d l a n d p s i 5 3 3 ( d o u b l e ...
x , d o u b l e c ) {
17 d o u b l e t = i p o w ( ( 1 . 0 - x ) , 5 ) ;
18 t = -2 217 6 . 0
*
t
*
i p o w ( c , 6 )
*
( 1 ) ;
19 r e t u r n t ;
20 }
Note that the polynomials wendlandpsi 5 3 1
and wendlandpsi 5 4 2 differ only by a multipli-
cation of a constant and a power of c, and both poly-
nomials are a representative of the Wendland function
ψ
5,2
.
The function ipow(x,i) evaluates x
i
where x is
a double and i is a positive integer. A possible efficient
implementation is given by:
Listing 3: Exponentiation routine.
1 / / F u n c t i o n f o r f a s t s q u a r i n g t o ...
i n t e g e r power
2 / / P o s t e d by u s e r E l i a s Y a rr k o v on ...
S t a c k o v e r f l o w .
3 s t a t i c d o u b l e i p o w ( d o u b l e b a s e , ...
i n t exp ) {
4 d o u b l e r e s u l t = 1 . 0 ;
5 f o r ( ; ; ) {
6 i f ( e xp & 1 )
7 r e s u l t
*
= ba s e ;
8 exp >>= 1 ;
9 i f ( ! e xp )
10 b r e a k ;
11 b a s e
*
= ba s e ;
12 }
13 r e t u r n r e s u l t ;
14 }
The functions wendlandpsi x y z have been
“flattened” in the sense that their domain is [0,1].
They require the user to premultiply the x value with
the chosen RBF-constant c > 0, that is for Ψ(x) =
ψ
l,k
(ckxk), the user needs to pass in the value ckxk
and c after ensuring that ckxk ∈ [0, 1]. A possible im-
plementation using the Armadillo library (Sanderson,
2010) could, for example, be:
Listing 4: Example usage.
1 d o u b l e p s i 3 ( c o n s t arma : : ve c &x , ...
d o u b l e c ) {
2 d o u b l e cx = c
*
arma : : norm ( x , 2 ) ;
3 r e t u r n ( cx < 1 . 0 ) ? ...
w e n d l a n d p s i 5 4 3 ( cx , c ) ...
: 0 . 0 ;
4 }
The tool is a simple Python script named wend-
landfunctions.py. When the script is run it outputs
text for code- and header-files, which contain the
Wendland function definitions. The user can supply
the script with a parameter --l and an integer value
m ≥ 2, in order to output code for Wendland functions
from ψ
2,1
up to ψ
m,i
for all 0 ≤ i < m.
5.1 Performance
In previous work (Bjornsson and Hafstein, 2018)
we have compared different method to evalute these
Wendland functions. The methods used for point
evaluation were:
• Having them in factorized form, as our software
tool provides, see Listing 1.
• Fully expanded polynomials and evaluated using
Horners Scheme, as in (Argaez et al., 2017).
• Precomputing the function in high precision (see
below) at 10
7
evenly spaced points on the interval
[0,1] and using them as a lookup table. That is,
look up the closes value.
• Using the same lookup table but additionally lin-
early interpolate between two nearest neighbours
to improve accuracy.
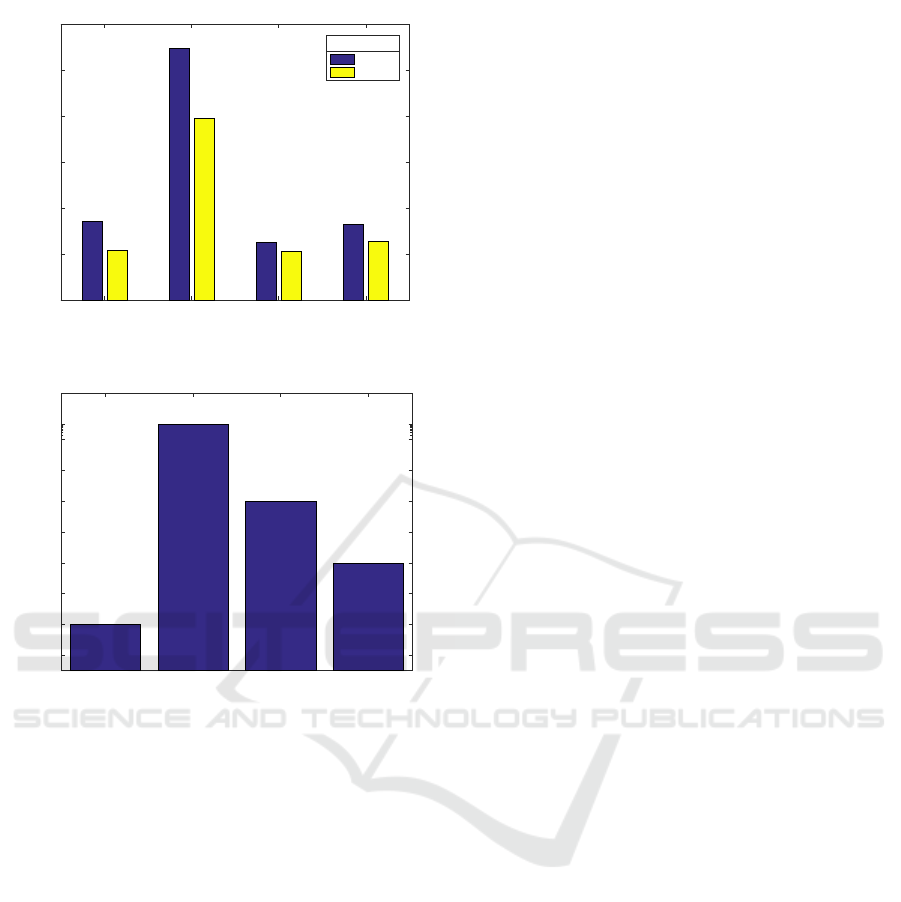
Figure 1 shows the performance of evaluating ψ
7,2
at 10
7
different points on the interval [0, 1], and Figure
2 shows the highest relative error at these points, with
these four different methods. To estimate the relative
error we calculated the value of the polynomial ψ
7,2
in
Matlab using variable precision arithmetic (VPA), up
to 32 significant digits, then rounded the value to the
closest double precision floating point number. Note
that the factorized form and Lookup-table are close
in speed, but the factorized form gives much greater
accuracy.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
160

Factorized Horner Lookup Lookup-interp
Method of evaluation
0
100
200
300
400
500
600
Time in ms
i5-8250U
i7-4790K
Processor
Figure 1: Running time of evaluating ψ
7,2
at 10
7
points.
Factorized Horner Lookup Lookup-interp
Method of evaluation
10
-15
10
-13
10
-11
10
-9
10
-7
10
-5
10
-3
10
-1
10
0
Relative error
Figure 2: Relative error of evaluations of ψ
7,2
. Note the
logarithmic scale of the y-axis.
6 CONCLUSION
We have developed an algorithm and created a tool to
generate a C/C++ library for Wendland’s compactly
supported Radial Basis Functions with arbitrary
parameters in a factorized form. This allows for the
efficient and numerically accurate evaluation of these
functions. This is desirable since previously they
were generated in a non-optimal form or had to be
evaluated by hand, which is a tedious and error prone
process. Additionally, the software generates a whole
family of Wendland functions suitable for solving
collocation problems for each initial Wendland
function ψ
l,k
and its support radius c
−1
. The tool
takes less than a second to output the .c and .h files
for all the Wendland function families up to and
including order 8.
ACKNOWLEDGEMENT
This research was supported by the Icelandic Re-
search Fund (Rann
´
ıs) in grant number 152429-051,
Lyapunov Methods and Stochastic Stability.
REFERENCES
Argaez, C., Hafstein, S., and Giesl, P. (2017). Wendland
functions - a C++ code to compute them. In Proceed-
ings of the 7th International Conference on Simulation
and Modeling Methodologies, Technologies and Ap-
plications - Volume 1: SIMULTECH,, pages 323–330.
INSTICC, SciTePress.
Bjornsson, H. and Hafstein, S. (2018). Verification of a nu-
merical solution to a collocation problem. In Proceed-
ings of the 15th International Conference on Informat-
ics in Control, Automation and Robotics - Volume 1:
CTDE,, pages 587–594. INSTICC, SciTePress.
Bjornsson, H., Hafstein, S., Giesl, P., Gudmundsson, S.,
and Scalas, E. (2019). Computation of the stochastic
basin of attraction by rigorous construction of a Lya-
punov function. Discrete and Continuous Dynamical
Systems-Series B (to appear).
Buhmann, M. (2000). Radial basis functions. In Acta nu-
merica, 2000, volume 9 of Acta Numer., pages 1–38.
Cambridge Univ. Press, Cambridge.
Buhmann, M. (2003). Radial basis functions: theory and
implementations, volume 12 of Cambridge Mono-
graphs on Applied and Computational Mathematics.
Cambridge University Press, Cambridge.
Burrus, C. S., Fox, J. W., Sitton, G. A., and Treitel, S.
(2003). Horner’s method for evaluating and deflating
polynomials. DSP Software Notes, Rice University,
Nov, 26.
Floater, M. and Iske, A. (1996). Multistep scattered data
interpolation using compactly supported Radial Basis
Functions. J. Comput. Appl. Math., 73(1-2):65–78.
Franke, C. and Schaback, R. (1998). Solving partial differ-
ential equations by collocation using radial basis func-
tions. Appl. Math. Comput., 93(1):73–82.
Giesl, P. (2007). Construction of Global Lyapunov Func-
tions Using Radial Basis Functions, volume 1904
of Lecture Notes in Mathematics. Springer-Verlag,
Berlin.
Giesl, P. (2008). Construction of a local and global Lya-
punov function using radial basis functions. IMA J.
Appl. Math., 73(5):782–802.
Giesl, P. and Hafstein, S. (2015). Computation and verifica-
tion of Lyapunov functions. SIAM Journal on Applied
Dynamical Systems, 14(4):1663–1698.
Hafstein, S., Gudmundsson, S., Giesl, P., and Scalas,
E. (2018). Lyapunov function computation for au-
tonomous linear stochastic differential equations us-
ing sum-of-squares programming. Discrete and Con-
tinuous Dynamical Systems - Series B, 23(2):939–950.
Khalil, H. (2002). Nonlinear systems. Pear, 3. edition.
Algorithm and Software to Generate Code for Wendland Functions in Factorized Form
161

Khasminskii, R. (2012). Stochastic stability of differential
equations. Springer, 2nd edition.
Mao, X. (2008). Stochastic Differential Equations and Ap-
plications. Woodhead Publishing, 2nd edition.
Sanderson, C. (2010). Armadillo: An open source C++
linear algebra library for fast prototyping and com-
putationally intensive experiments. Technical report,
NICTA.
Sastry, S. (1999). Nonlinear Systems: Analysis, Stability,
and Control. Springer.
Vidyasagar, M. (2002). Nonlinear System Analysis. Clas-
sics in applied mathematics. SIAM, 2. edition.
Wendland, H. (1998). Error estimates for interpolation by
compactly supported Radial Basis Functions of mini-
mal degree. J. Approx. Theory, 93:258–272.
Wendland, H. (2005). Scattered data approximation, vol-
ume 17 of Cambridge Monographs on Applied and
Computational Mathematics. Cambridge University
Press, Cambridge.
Wendland, H. (2017). Multiscale radial basis functions.
In Frames and other bases in abstract and function
spaces, Appl. Numer. Harmon. Anal., pages 265–299.
Birkh
¨
auser/Springer, Cham.
Wu, Z. (1992). Hermite-Birkhoff interpolation of scattered
data by radial basis functions. Approx. Theory Appl.,
8(2):1–10.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
162