The Problem of Finding the Best Strategy for Progress Computation in

Adaptive Web Surveys

Thomas M. Prinz, Jan Pl

otner and Anja Vetterlein

Course Evaluation Service, Friedrich Schiller University Jena, Am Steiger 3 Haus 1, Jena, Germany

Keywords:

Progress Indicator, Prediction Strategy, Fit Measure, Web Survey, Interaction.

Abstract:

Web surveys are typical web information systems. As part of the interface of a survey, progress indicators inform

the participants about their state of completion. Different studies suggest that the progress indicator in web

surveys has an impact on the dropout and answer behaviour of the participants. Therefore, researchers should

invest some time in ﬁnding the right indicator for their surveys. But the calculation of the progress is sometimes

more difﬁcult than expected, especially, in surveys with a lot of branches. Current related work explains the

progress computation in such cases based on different prediction strategies. However, the performance of these

strategies varies for different surveys. In this position paper, we explain how to compare those strategies. The

chosen Root Mean Square Error measure allows to select the best strategy. But experiments with two large

real-world surveys show that there is no single best strategy for all of them. It highly depends on the structure of

the surveys and sometimes even the best known strategy produces bad predictions. Dedicated research should

ﬁnd solutions for these cases.

1 INTRODUCTION

Web surveys present items (questions) in a paper-like

format with various input ﬁelds. The survey itself

interacts with a server application and transfers the

inserted answers of the participants to it. In other

words, web surveys are web information systems.

The interface of a web survey is intuitive and

straight-forward in the common case. Besides the

input ﬁelds for answers, web surveys consist usually

of buttons to precede and sometimes also to recede in

the survey. Headers inform the participant about the

context of the survey and usually Progress Indicators

(PIs) inform the participants about the state of com-

pletion. This paper focuses on the PIs as part of the

interface.

Typically, the PI displays the progress in percent-

age between

and

100%

. Unlike PIs of usual tasks in

general software, participants of web surveys have to

focus on the task (the survey), can inﬂuence the PI, and

do not necessarily have an interest on the result (Villar

et al., 2013). Therefore, PIs in web surveys are differ-

ent from those of other software (Villar et al., 2013),

e. g., for machine learning (Luo, 2017) and database

queries (Li et al., 2012).

Participants in web surveys prefer to have a PI

(Myers, 1983; Villar et al., 2013) to be aware of their

progress. However, the computation of the progress

can be difﬁcult in case of surveys with adaptivity

(branches). (Prinz et al., 2019) propose an equation to

compute the progress in adaptive surveys. The equa-

tion is based on the number of remaining items (ques-

tions) at each point of time. This number of remaining

items depends on a chosen prediction strategy. Such

a strategy tries to predict the number of remaining

items for each page since the participants may take

different paths in the survey with different numbers of

remaining items. For example, two known prediction

strategies are: 1) take the minimum or 2) maximum

number of remaining items (Kaczmirek, 2009). How-

ever, (Prinz et al., 2019) suspects that it depends on

the structure of the survey which prediction strategy is

the best. Furthermore, the comparison of the quality

of the strategies seems to be not trivial.

One goal of this paper is to have a measure to

select that prediction strategy, which guesses the true

number of remaining items and, therefore, the true

progress as well as possible. We support the idea of

displaying the true progress since research in Human-

Computer Interaction (HCI) reveals high probable side-

effects of PIs on the answer and dropout behaviour

of participants (Villar et al., 2013). Especially the

progress speed (the rate in which the PI increases)

seems to inﬂuence the decision whether a participant

Prinz, T., Plötner, J. and Vetterlein, A.

The Problem of Finding the Best Strategy for Progress Computation in Adaptive Web Surveys.

DOI: 10.5220/0008345403070313

In Proceedings of the 15th International Conference on Web Information Systems and Technologies (WEBIST 2019), pages 307-313

ISBN: 978-989-758-386-5

307

ﬁnishes a long survey (Myers, 1985; Villar et al., 2013).

PIs increasing faster at the start and slower at the end

seem to encourage the participant to ﬁnish the survey.

On the contrary, if a PI is slow at the beginning and gets

faster at the end seems to discourage and causes higher

dropout rates (Conrad et al., 2003; Matzat et al., 2009;

Conrad et al., 2010). A meta-analysis of PI speeds by

(Villar et al., 2013) supports these observations.

The long-term effects of different PI speeds are not

researched. Even though more participants complete

a survey by using a fast-to-slow increase of the PI, if

the participants become aware of the varying PI speed,

it might decrease their willingness to participate in

future surveys by the survey provider. Instead, PIs

which try to display the true progress are honest to the

participants and should reduce side-effects of PIs.

In this position paper, we argue that the Root Mean

Square Error (RMSE) is a useful measure to describe

the quality of prediction strategies for progress com-

putation. This measure allows to compare uses of

strategies and to choose the “best” one. Researchers

conducting surveys can use the RMSE to determine

the best known strategy for their surveys and can give

the participant a PI, which represents the true progress

as well as possible. Furthermore, this paper shows

that the yet known trivial prediction strategies lead to

bad predictions in some cases. Further research should

ﬁnd solutions for these cases.

The paper has the following structure: At ﬁrst, it

explains in Section 2 how we can compute the progress

in adaptive surveys and how we can apply the predic-

tion strategies. Based on this computation, the pa-

per presents four measures for the determination of

the quality of a prediction strategy in Section 3 and

shows their application in Section 4. Section 4 argues

further which measure is most suitable and explains

some disadvantages with current prediction strategies.

Section 5 ends the paper with a brief discussion and

conclusion.

2 PROGRESS COMPUTATION

Although a lot of studies consider the differences in PI

speeds, the computation of an accurate progress in web

surveys (especially in surveys with high adaptivity) is

not in the research focus. The thesis of (Kaczmirek,

2009) and the work of (Prinz et al., 2019) based on

it are the only available work to the best knowledge

of the authors, which try to answer how to calculate

the progress in web surveys with adaptivity. The lack

of knowledge about the “path” a participant takes in a

survey, is the main problem in progress computations.

Prinz et al. propose an algorithm, which supports

item

pageedge

start

page

end

page

branch

Figure 1: A simple questionnaire graph.

different prediction strategies. By applying one of

several strategies it is possible to approximate the true

progress as well as possible.

The approach with different prediction strategies

is based on an abstract survey model called the ques-

tionnaire graph (in short Q-graph). The Q-graph de-

scribes the structure of questionnaires. It is an acyclic,

connected digraph

Q = (P, E)

with a set of pages

P = P(Q)

and a set of edges

E = E(Q)

, which con-

nect the pages. The Q-graph

has exactly one page

without any incoming edge (the start page) and exact

one page without any outgoing edge (the end page).

A page

P ∈ P(Q)

is a ﬁnite set

,...}

of items

,. ..

. For this reason,

|P|

is the number of items

on page

. For reasons of simplicity, each item is

assumed to be unique. Figure 1 illustrates a simple

Q-graph.

The edges build paths throughout the Q-graph. A

path is a sequence

W = (P

,. .. ,P

)

m ≥ 0

, of pages,

,. .. ,P

∈ P(Q)

. For this sequence, there is an edge

for each two pages appearing consecutively:

∀0 ≤ i <

m: (P

i+1

) ∈ E(Q).

(Prinz et al., 2019) propose a general equation to

compute the progress for arbitrary Q-graphs. The equa-

tion is recursive and returns values between

and

(i. e., 0 and 100%):

ρ(P) = ρ(P

) + |P|

1 −ρ(P

)

rem(P)

(1)

The equation contains the following parts:

ρ(P)

de-

scribes the progress at the current page

. The com-

putation of the current progress needs the progress

ρ(P

)

of the previous page

. If the current page

is the ﬁrst page of the Q-graph, then it is assumed

that

ρ(P

)

. The equation adds the impact on

the progress of the current page,

|P|

1−ρ(P

)

rem(P)

, to the

progress of the previous page.

|P|

is the number of

items on the current page. The impact of a single item

on the progress on the current page is

1−ρ(P

)

rem(P)

. It

contains the remaining progress (

1 −ρ(P

)

) and the

number of remaining items (

rem(P)

). The usage of the

remaining progress in the equation allows the progress

to adopt to the number of remaining items. For exam-

ple, if a participant follows a branch, which reduces

the number of remaining items, then the impact of

each item increases, accelerating the growth of the PI.

WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies

308

Input: A Q-graph Q and a selection operator t.

Output: For each P ∈ P(Q) the remaining items rem(P).

Set rem(P) = 0 for each P ∈ P(Q)

worklist ←queue



P(Q)



,visited ←

while worklist 6=

0 do

P ←dequeue(worklist)

directSucc ← {succ : (P, Succ) ∈ E(Q)}

if directSucc ⊆ visited then

if directSucc =

0 then

rem(P) ← |P|

else if |directSucc|= |{Succ}| = 1 then

rem(P) ← |P|+ rem(Succ)

else

rem(P) ← |P|+

Succ∈directSucc

rem(Succ)

visited ←visited ∪{P}

else

enqueue(worklist,P)

Figure 2: The general algorithm for computing the number

of remaining items for arbitrary prediction strategies (taken

from (Prinz et al., 2019)).

Otherwise, if the number of remaining items increases,

the impact with each item decreases, decelerating the

growth of the PI.

At the beginning of an adaptive survey, the path,

a participant takes, is unknown which makes it neces-

sary to predict the number of remaining items

rem(P)

But different prediction strategies are possible making

the computation of the progress a challenge. (Prinz

et al., 2019) deﬁned a general algorithm for comput-

ing the number of remaining items

rem(P)

for each

page for arbitrary prediction strategies. A property of

the algorithm is the usage of a selection operator

representing these strategies. The algorithm receives

the selection operator as input making the algorithm

independent from the operator. Figure 2 shows the

algorithm. In this paper, we focus on the description

of the selection operator. For a more general overview,

see (Prinz et al., 2019).

There are exactly three situations during the com-

putation of the remaining items for a page

. Either

has 1) no successor, 2) exactly one direct successor,

or 3) more than one direct successor. The number

of remaining items for the ﬁrst both situations is the

sum of the number of items on

|P|

, and the number

of remaining items

rem(Succ)

of the direct successor

Succ

(or

in the case of situation 1)). In situation

3), different numbers of remaining items may reach

via the direct successors

Succ

.. .

Succ

n ≥ 2

The selection operator receives all those numbers as

input,



rem(Succ

),. .. ,rem(Succ

)



, and produces

a single prediction for

rem(P)

. The algorithm contains

these situations in the inner if-then-else-structure.

Typical examples of selection operators are the

minimum and maximum functions. Taking the mini-

mum, the number of remaining items is the smallest

number of items. The progress is fast at the beginning

and becomes slower if the participant takes a path con-

taining more items than the operator has detected. For

the maximum, it is vice versa. It represents the largest

number of items.

3 MEASURES TO COMPARE

PREDICTION STRATEGIES

Different prediction strategies usually result in differ-

ent predicted progresses. Since a survey needs a single

strategy, which provides the best prediction, we need

a measure to compare the precision of such strategies.

A PI in a survey should commonly represent the

true progress as well as possible. The computation

of the true progress needs the exact number of re-

maining items. However, a survey engine knows this

exact number only after the participant is ﬁnished. In

other words, only after a participant completes a path

W = (P

,. .. ,P

)

n ≥ 1

, then the computation knows

the exact number of remaining items on each page

,. .. ,P

and can compute the true progress ρ

∗

A strategy within a set of prediction strategies

,. .. ,t

}

n ≥ 1

, is the best one if it minimizes

the discrepancy between the predicted and the true

progress best. Many measures regarding prediction

accuracy are proposed in literature and a lot of recom-

mendations explain in which situations a speciﬁc mea-

sure should be used. (Hyndman and Koehler, 2006)

consider different measures of prediction accuracy in

detail and provide a good overview about them. All

the measures have in common that they are based on

the difference between the prediction and the actual

measured value (in our speciﬁc case, the true progress).

Our basic idea is that we set the true and pre-

dicted/displayed progress in relation. That means,

we have a value pair



∗

(P),ρ(P)



of the true and

displayed progress for each page

on a path a par-

ticipant has visited. The pair



∗

(P),ρ(P)



can be

read as “on page

the true progress was

∗

(P)

but

the progress

ρ(P)

was displayed”. If the predicted

progress differs from the true progress, it results in an

error

e(P) = ρ(P)−ρ

∗

(P)

. All the pairs



∗

(P),ρ(P)



can be computed for a prediction strategy and it results

in a set

, which contains all of these pairs. For the

comparison of different strategies

.. .

n ≥ 2

there is such a set for each strategy: M

, .. ., M

Notice that

∗

and

have percentage scales. That

means, measures based on percentage errors are ap-

plicable. (Hyndman and Koehler, 2006) mention four

typical measures of percentage errors:

1. Mean Absolute Error (MAE), |e|

The Problem of Finding the Best Strategy for Progress Computation in Adaptive Web Surveys

309

2. Median Absolute Error (MdAE), median(|e|)

3. Root Mean Square Error (RMSE),

Root Median Square Error (RMdSE),

median(e

Applying one of the measures produces a value

val

for each strategy

1 ≤i ≤n

. Since the true progress

is always the same for each strategy and all values are

on the percentage scale, statistics allows us to compare

the different values. The strategy with the lowest value

is the best one of the considered strategies.

A value of

is perfect for all measures, it means

that the error between the true and predicted progress

is zero. The RMSE and RMdSE have the disadvan-

tage that they are inﬁnite, undeﬁned, or skewed if

all observed values are

or near to

(Hyndman and

Koehler, 2006). Since the true progress has values in

the range from

100%

, this disadvantage does not

affect them.

The approach relies on the knowledge of the true

progress and, therefore, on empirical data. Unfortu-

nately, as with any empricial study, these data is usu-

ally not available before the survey starts. To overcome

this problem, data can be generated by pilot studies,

simulations, or path-explorations of the survey for ex-

ample. Pilot studies refer to conducting the survey

with a subset of the population, whereas in simulations

virtual participants answer the questionnaire. In a path-

exploration, an algorithm computes all (or most) paths

of the survey and computes sample progresses for each

path. But adaptive surveys may have a (exponential)

large number of such paths. Furthermore, all three

possibilities have in common that they should repre-

sent a “realistic” usage of the different paths. Different

weights exist for the paths and inﬂuence the measure.

The researcher should be aware of this.

4 EXPERIMENTS AND LESSONS

LEARNED

In our department, we conduct large surveys with hun-

dreds of variables and items and many adaptive paths.

The survey engine, that we use, stores the paths on

which the participants “walk” through the surveys. For

each participant, it is possible to compute the true num-

ber of remaining items for each visited page. Besides

the true progress, we can also compute the predicted

progress for different prediction strategies in retrospect

with Equation 1 and the algorithm of Figure 2. As a

result, we get data sets with the true and displayed

progresses for each strategy for each participant. With

these it is possible to determine the most suitable mea-

sure and the best strategy.

4.1 Experimental Settings

We took two of our surveys, survey A and survey B.

Table 1 describes the structure of the surveys based

on empirical data. In the table,

Branches

refers to the

number of pages with branches,

|Path|

is the number of

pages within a path, and

Items

refers to the number of

items a participant has seen. Both surveys have similar

characteristics except for

Participants

and

Branches

. For

survey A we have more available data sets, whereas

survey B has much more branches.

For both surveys, we produced data sets for three

different prediction strategies: minimum (min), mean,

and maximum (max). If a page has more than two

direct successor pages, the minimum strategy takes the

smallest number of remaining items. The maximum

strategy takes the largest number of remaining items

in such a case, whereas the mean strategy computes

the mean number. At this place, it is important that the

mean represents not the empirical mean of items on

all empirical paths. It represents the selection operator

mean used in the general algorithm. The expected

remaining items on the start page vary for both surveys

(cf. Table 1,

rem(start)

) and are higher for survey

B except for the min approach, which is very small

with a value of

. The values in parentheses represent

adjustments on the surveys explained in the following.

4.2 Lessons Learned

Screening paths are paths at the start of a survey in

which a participant receives a few key questions to

determine if they are part of the speciﬁc target popu-

lation. Depending on their answers, the survey either

continues to the main part or ends quickly. Therefore,

there is an exit path to the end without many items.

The ﬁrst lesson we learned was that the inclusion of

screening paths in the progress calculation usually pro-

duces bad predictions. By taking the min strategy, the

exit path has the fewest remaining items and, there-

fore, decreases the number of remaining items on all

paths at the beginning of the survey (cf.

rem(start)

Table 1). In survey B, this leads to progresses near

100%

after passing the page where the screening path

ends. For the strategies mean and max, the screening

path does not have a great impact.

Adaptive page chains are subpaths with many adap-

tive pages, however, each participant only sees a small

number of them. In survey B, there are a lot of such

pages, which contain items about special topics. In

general, each participant has only seen one or two of

these approx. 30 pages. For min, such chains dis-

appear which skews the results as most participants

see at least one page. The max strategy includes each

WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies

310

Table 1: Structure and important empirical properties of survey A and survey B.

Survey A Survey B Survey A Survey B

Participants

1041 193 N

Items

Branches

11 38 min 4 6

|Path| mean 246.70 290.97

min 2 2 max 339 377

mean 16.34 18.49 rem(start)

max 25 23 t = min 46 (167) 7 (258)

Var 48.56 24.63 t = mean 115 (241) 254 (495)

t = max 345 (288) 706 (700)

Participants

number of participants,

Branches

number of branching pages in Q-graph,

|Path| =

empirical length of

paths,

Items

empirical number of items seen,

rem(start) =

remaining items on the start page (values in parentheses

are adjustments explained in the text)

adaptive page resulting in a high number of remaining

items. The mean strategy smooths the high number

of remaining items, however, usually only by half. In

Table 1,

Branches

indicates long adaptive page chains

with a value of

in survey B instead of

in A. The

second lesson we learned was that such chains of adap-

tive pages produce bad predictions too.

As a consequence, we adjusted our experiments

with the surveys A and B by removing the screening

paths from the progress computation. Otherwise, it

is meaningless to compare the results of the different

strategies. The adjustments result in different numbers

of remaining items for each strategy (see

rem(start)

parentheses in Table 1). We left the chains of adaptive

pages as they contain important items.

4.3 Experimental Results

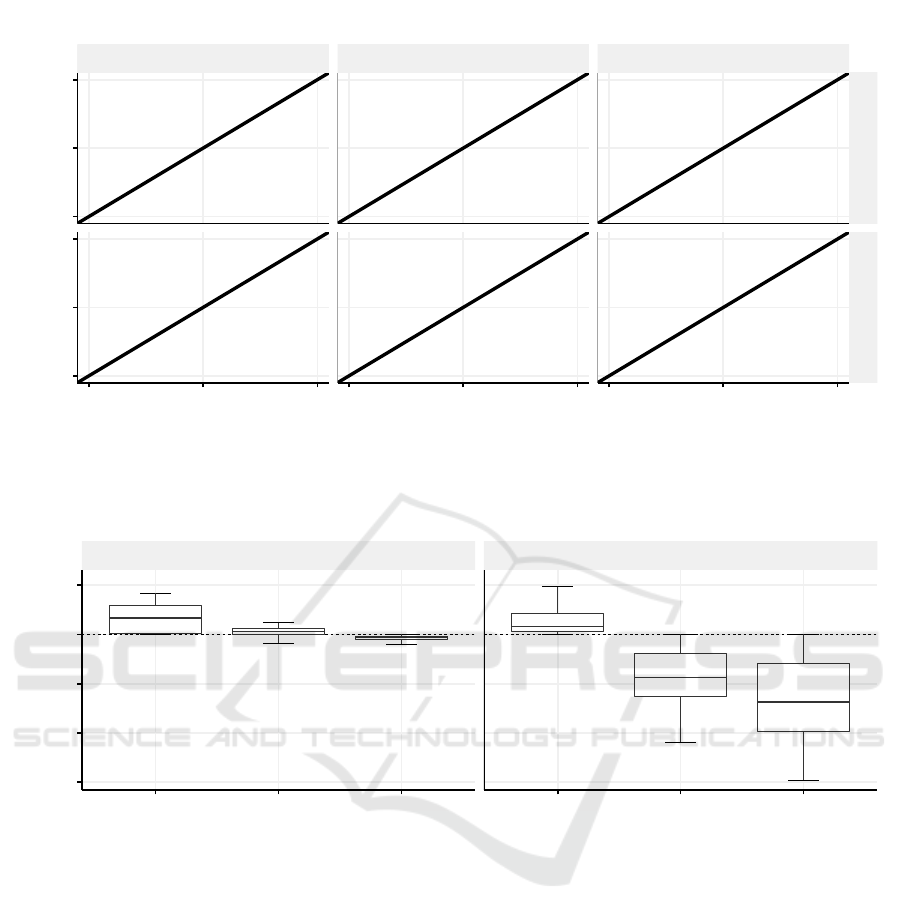
Figure 3 shows the results of our experiments. The

axis describes the true and the

axis the displayed

(predicted) progress for each strategy. The black line

illustrates a perfect prediction strategy and the true

progress, respectively. An observation is that the min

approach results in overestimations of the progress,

whereas the max approach results in underestimations.

For survey A, mean has values above and below the

true progress line. For survey B, the values of mean are

all below the line because of the mentioned adaptive

page chains.

Figure 3 contains the values for the four mea-

sures MAE, MdAE, RMSE, and RMdSE. Actually,

the MdAE and RMdSE result in nearly equivalent val-

ues. The Appendix explains why.

For survey A, the mean strategy has the lowest

MAE of

1.47

and RMSE of

2.13

, but the max strategy

has the lowest MdAE and RMdSE with both

1.08

The mean and max strategy seem to estimate the true

progress best. The min approach is the worst approach.

The distribution of the points supports the result.

For survey B, the strategies perform differently:

the min approach is the best and the max strategy is the

worst one for all four measures. However as a whole,

all strategies perform worse in survey B. There is no

strategy which predicts the true progress well. Even

though min is the best strategy of the three, a visual

inspection of the predicted values in Figure 3 shows

that for many participants the displayed progress is

near

100%

even though they still have around

25%

of the survey to go. A reason for this behaviour are

the adaptive page chains corresponding with a high

number of branching pages (cf. Table 1,

Branches

The poor ﬁt is supported by higher values instead of

those for survey A. The worse ﬁtting for survey B

could also be a result of the small number of available

participants.

In our application context, high errors should be

penalized more than smaller errors since higher errors

have a stronger impact on the overall progress calcu-

lation and can lead to noticeable deviations from the

true progress whereas small errors should be almost

invisible to the participant. The RMSE is, therefore, a

good choice, because it squares the error giving large

errors more weight. Like Figure 3 shows, the RMSE is

always the highest. Actually, the value of the RMdSE

is always close to the MdAE as mentioned before. The

squaring of the error in the RMdSE has not a great

effect on the resulting value, as also shown in the Ap-

pendix.

For survey A, the mean (MAE and RMSE) as well

as the max strategy (MdAE and RMdSE) have small

values as mentioned before. Figure 3 shows that the

max strategy has more outliers for survey A than the

mean strategy. Following the above argumentation, the

mean strategy should be used since the outliers may

lead to noticeable deviations. This is supported by a

higher RMSE.

Altogether, we recommend to use the RMSE for

comparing different prediction strategies for PIs. It is

most sensitive to high deviations.

Figure 4 shows the error distribution for all strate-

gies in both surveys. For survey A, the mean and max

strategies result in errors near zero with less variance

The Problem of Finding the Best Strategy for Progress Computation in Adaptive Web Surveys

311

●

●●

●

●●

●

●●●●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●●

●

●●●

●

●●

●

●●

●

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

●

●●

●

MAE = 6.64

MdAE = 6.69

RMSE = 8.38

RMdSE = 6.69

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

MAE = 5.46

MdAE = 3.36

RMSE = 7.91

RMdSE = 3.36

●

●●

●

●●

●

●●●●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●●

●

●●●

●

●●

●

●●

●

●●

●

MAE = 1.47

MdAE = 1.3

RMSE = 2.13

RMdSE = 1.3

●

MAE = 17.63

MdAE = 17.45

RMSE = 21.36

RMdSE = 17.45

●

●●

●

●●

●

●●●●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●

●

●●●

●

●●●

●

●●

●

●●

●

●●

●

MAE = 1.67

MdAE = 1.08

RMSE = 2.65

RMdSE = 1.08

●

MAE = 26.28

MdAE = 27.37

RMSE = 31.3

RMdSE = 27.37

min

mean

max

Survey A

Survey B

0 50 100 0 50 100 0 50 100

100

True Progress in %

Displayed Progress in %

Figure 3: Charts with displayed progresses and the computed measures MAE, MdAE, RMSE, and RMSE for the three

prediction strategies min, mean, and max for two surveys A and B. For survey A, the mean strategy has the lowest MAE and

RMSE and the max strategy has the lowest MdAE and RMdSE. For survey B, the min approach is the best and the max strategy

is the worst one for all four measures. But all strategies perform worse in survey B.

●

●●

●

Survey A

Survey B

min mean max min mean max

−0.6

−0.4

−0.2

0.0

0.2

Error

Figure 4: Error distribution of the strategies min, mean, and max for surveys A and B. For survey A, the mean and max strategies

result in errors near zero with less variance. The min strategy has a higher variance. In contrast, for survey B, the max and

mean strategies have a very high variance and the min approach has a small variance.

and only a minor number of outliers. Instead, the min

strategy has a higher variance of the error. The max

and mean strategies have a very high variance for sur-

vey B. The min approach has better results with a small

variance. Altogether, Figure 4 supports the previous

observations and the usage of the RMSE.

5 BRIEF DISCUSSION AND

CONCLUSION

In this paper, we argued for a measure to compare pre-

diction strategies for the computation of the progress in

adaptive surveys. Experiments suggest that the RMSE

is a good choice of measure. The measure is compa-

rable between different strategies for the same survey.

The strategy with the lowest RMSE is the best con-

sidered one. Our experiments with real-world surveys

accentuate the hypothesis that there is not a single best

prediction strategy for all surveys. The right strategy

depends on the survey.

Using the RMSE for comparing the strategies

needs empirical data. Further research has to ﬁnd ways

to generate this data precisely, e. g., by simulation or

path-weighting.

Although a prediction strategy has the best RMSE

within a set of strategies, another strategy may be bet-

ter, e. g., if the simulated data does not reﬂect the actual

population behaviour; or there is simply an yet un-

known strategy, which approximates the true progress

better. We presented three basic strategies, but fu-

ture research should focus on ﬁnding better strategies,

which can handle adaptive chains.

WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies

312

Furthermore, results of the state-of-the-art should

be considered for the decision of which strategy is

used. For example, if the min and max strategies per-

form similarly, it states to use the min strategy as it

may reduce the dropout rate. In future work, we want

to build a tool, which chooses the best of a set of strate-

gies and includes the state-of-the-art. It should also

provide a time estimate at each page of the survey.

Furthermore, we also want to consider how we can

inform the participants about variances in the progress

and how that information inﬂuences the participant’s

satisfaction.

REFERENCES

Conrad, F. G., Couper, M. P., and Tourangeau, R. (2003). Ef-

fectiveness of progress indicators in web surveys: It’s

what’s up front that counts. In Banks, R., editor, Survey

and statistical computing IV. The impact of technology

on the survey process, volume V, pages 1 – 10, London,

England. Association for Survey Computing.

Conrad, F. G., Couper, M. P., Tourangeau, R., and Peytchev,

A. (2010). The impact of progress indicators on task

completion. Interacting with computers, (5):417—427.

Hyndman, R. J. and Koehler, A. B. (2006). Another look at

measures of forecast accuracy. International Journal

of Forecasting, 22(4):679–688.

Kaczmirek, L. (2009). Human Survey-Interaction. Usability

and Nonresponse in Online Surveys. Number 6 in Neue

Schriften zur Online-Forschung. Herbert von Halem

Verlag, Cologne, Germany, 1 edition.

Li, J., Nehme, R. V., and Naughton, J. (2012). GSLPI: A

Cost-Based Query Progress Indicator. In 2012 IEEE

28th International Conference on Data Engineering,

pages 678–689.

Luo, G. (2017). Toward a Progress Indicator for Machine

Learning Model Building and Data Mining Algorithm

Execution: A Position Paper. SIGKDD Explor. Newsl.,

19(2):13–24.

Matzat, U., Snijders, C., and van der Horst, W. (2009). Ef-

fects of Different Types of Progress Indicators on Drop-

Out Rates in Web Surveys. Social Psychology, (40):43–

52.

Myers, B. A. (1983). INCENSE: A System for Display-

ing Data Structures. SIGGRAPH Comput. Graph.,

17(3):115–125.

Myers, B. A. (1985). The Importance of Percent-done

Progress Indicators for Computer-human Interfaces.

SIGCHI Bull., 16(4):11–17.

Prinz, T. M., Bernhardt, R., Pl

otner, J., and Vetterlein, A.

(2019). Progress Indicators in Web Surveys Reconsid-

ered — A General Progress Algorithm. In Kokil, U.

and Ota, T., editors, ACHI 2019: The Twelfth Interna-

tional Conference on Advances in Computer-Human

Interactions, Athens, Greece, February 24–28, 2019.

Proceedings, volume 9, pages 101–107. IARIA Con-

ference, ThinkMind Digital Library.

Villar, A., Callegaro, M., and Yang, Y. (2013). Where Am

I? A Meta-Analysis of Experiments on the Effects of

Progress Indicators for Web Surveys. Social Science

Computer Review, 31(6):744–762.

APPENDIX

Section 4 mentioned that the MdAE and RMdSE

mostly result in almost the same values. In this ap-

pendix, we are going to investigate this fact a little

more closely.

Assume a vector of (real) values

v = {v

,. .. ,v

}

n ≥1

. The ﬁrst step of computing the median

˜v

is to

order the values of

by size. By taking the MdAE, the

ordering is performed on

|v|

. For RMdSE, the ordering

is performed on

. Since for each two arbitrary (real)

values

and

it holds true that

|≤|v

| ⇐⇒ v

≤

, it is easy to conﬁrm that the ordering of

|v|

is equal

to the ordering of

. Let

,. .. ,a

)

be the resulting

order of the absolute and

,. .. ,s

)

be the ordering

for the squared values. The following is valid:

∀1 ≤ i ≤n : a

√

(2)

The second step of computing the median depends on

the number of dimensions

. There are two cases:

1. n

is odd. The median is the value on position

of the ordering. It is

for MdAE and

for

RMdSE. For RMdSE, we have to take the root

median, i. e., RMdSE is

√

. With Equation 2 in

mind, the MdAE and RMdSE are equal.

2. n

is even. The median is half the sum of

the values on positions

and

/2 + 1

. It is

/2(a

+ a

/2+1

)

for MdAE and

/2(s

+ s

/2+1

)

for RMdSE. For RMdSE, we take again the rooted

median,

/2(s

+ s

/2+1

)

. Actually, the MdAE

and RMdSE are unequal. But on closer inspection,

the value of

/2(s

/2+1

)

is always between

and

/2+1

, and therefore, the RMdSE is always be-

tween a

and a

/2+1

with regard on Equation 2.

Both cases result in the following facts:

1. MdAE and RMdSE are equal if n is odd.

MdAE and RMdSE are almost equal if

is even

and the values on positions

and

/2 +1

are close

to each other.

The Problem of Finding the Best Strategy for Progress Computation in Adaptive Web Surveys

313