Iterated Local Search: Applications and Extensions

Helena Ramalhinho

Universitat Pompeu Fabra, Spain

Keywords: Metaheuristics, Iterated Local Search, Applied Combinatorial Optimization.

Abstract: Iterated Local Search (ILS) is a conceptually simple and efficient well-known Metaheuristic. The main idea

behind ILS is to drive the search not on the full space of all feasible solutions but on the solutions that are

returned by some underlying algorithm; typically, local optimal solutions obtained by the application of a

local search heuristic. This method has been applied to many different optimization problems having about

10,000 entries in Google Scholar. In this talk, we will review briefly the ILS method emphasizing the

extensions of ILS. We will describe three relevant types of extensions: the hybrid ILS approaches combining

ILS with other metaheuristics and/or exact methods; the SimILS (Simulation+ILS) to solve Stochastic

Combinatorial Optimization Problems; the MoILS to solve Multiobjective Combinatorial Optimization,

including multiobjective and stochastic problems. We will discuss the advantages and disadvantages of these

extensions and present some applications, including real ones in areas like Marketing, Supply Chain

Management, Logistics or Health Care.

1 INTRODUCTION

Optimization problems have been always relevant for

businesses and other organizations, to improve the

use of the resources and also to reduce the overall

system cost. In today’s world, with the availability of

large amount of data and with the increase complexity

of the problems, it is more important than ever to be

able to solve efficiently the optimization problems.

Optimization problems can appear in all areas of

business from marketing to logistics, in public

organizations, in health care organizations and even

in NGO’s entities. Therefore, being able to solve

these large-scale complex problems is a relevant and

very actual area for researchers and managers. In

many cases, within the Optimization area, the best

(and only) solution approach to solve these complex

problems are the metaheuristics.

In the optimization literature we can find two

general types of solution methods: exact methods

and, heuristics and metaheuristics. An exact or

optimal method in the optimization context refers to

an algorithm that computes an optimal solution. A

heuristic algorithm (often shortened to heuristic) is a

solution method that does not guarantee

mathematically an optimal solution, but in general

http://orcid.org/0000-0003-3174-3432

has a good level of performance in terms of solution

quality or convergence, within a very short

computational time. Heuristics may be constructive

(producing a single solution) or local search (starting

from one constructive or random solution and moving

iteratively to other nearby solutions) or a combination

(constructing one or more solutions and using them to

start a local search). A metaheuristic is a framework

for producing heuristics, such as simulated annealing,

tabu search or genetic algorithms. To develop an

heuristic for a particular problem some problem-

specific characteristics must be defined, but some

other can be general for all problems. The problem-

specific may include the definition of a feasible

solution, the neighborhood of a solution, rules for

changing solutions, and rules for setting certain

parameters during the course of execution. In the last

years, many metaheuristics have been proposed and

successfully applied to solve complex and large-scale

problems in many areas (Martí et al. 2018).

In this work, we focus on a metaheuristic known

as Iterated Local Search (ILS). ILS is one of the most

popular single-solution based metaheuristics. ILS is

recognized by many authors as a relatively simple yet

efficient framework able to deal with complex

optimization problems. In particular it is a very

Ramalhinho Lourenço, H.

Iterated Local Search: Applications and Extensions.

DOI: 10.5220/0008345800070015

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 7-15

ISBN: 978-989-758-352-0

successful method when applied to Combinatorial

Optimization Problems (COPs), including problems

in Logistics, Transportation, Scheduling, Heath care,

Marketing, etc. The success of the ILS can be

explained because it has many of the desirable

features of a metaheuristics: accuracy, speed,

simplicity and flexibility (Cordeau et al. 2002).

The main objective of this work is to give an

accessible description of the underlying principles of

ILS and a discussion of basic implementation issues.

Next, we present extensions of the application of the

ILS: the hybrid ILS approaches combining ILS with

other metaheuristics and/or exact methods; the

SimILS (Simulation+ILS) to solve Stochastic

Combinatorial Optimization Problems; the

MoILS/MoSimILS to solve Multiobjective

(Stochastic) Combinatorial Optimization. We will

discuss the advantages and disadvantages of these

extensions and present some applications, including

real ones in areas like Marketing, Supply Chain

Management, Logistics or Health Care. We will

review the main work done by the author in the area

of Iterated Local Search.

2 ITERATED LOCAL SEARCH

The Iterated Local Search can be seen as an extension

of the well know algorithm know as Local Search

(LS). Local Search have been applied extensively to

combinatorial optimization problems (COPs). A LS

method consists in finding an initial solution, usually

using a constructive or random heuristic, and then

perform a neighborhood search until a local optimal

solution is found. For each specific problem, a

neighborhood must be defined. This neighborhood

consists usually in a set of solutions that can be

obtained from the incumbent solution by performing

small modifications, known as moves. For all or

almost all COPs, it is relatively simple to obtain an

initial solution and define a neighborhood. Therefore,

a LS can be defined by using these two concepts.

The main issue with such a simple LS method, is

that usually the local optimal solution obtained is far

away from the overall optimal solution, i.e. the

quality of the solutions obtained is not too good. To

avoid this issue, we can use a random initial solution

and apply to each one a LS approach. This is known

as Random Restart approach. This simple random

sampling approach can perform poorly, in

particularly if the instance size is large. ILS belongs

to a category of multi-start metaheuristics that

improve the performance of the simple Random

Restart by incorporating more sophisticated

procedures (Martí et al. 2013). In this way, ILS tries

to avoid the disadvantages of random restart by

exploring the solution space using a walk that steps

from one local optimal solution to a “nearby” one. To

implement this idea, another phase is included in the

LS that allows to “restart” the search but try not to

“lose” the good properties and components of the

solutions already obtained. This component we call it

“Perturbation” Phase.

We can know present the Iterated Local Search

that consists in four main phases: Generate an Initial

Solution, Local Search, Perturbation and Acceptance

Criterion.

First of all, an initial solution is constructed

(Generate an Initial Solution), afterwards a Local

Search method is applied to obtain a local optimal

solution (current solution). Next, a random

Perturbation phase is applied to obtain a different

solution changing some components of the current

solution followed by applying again a Local Search

method. If the solution obtained passes an

Acceptance Criterion test, it becomes the next

current solution; otherwise, one returns to previous

one. In any case, the process is repeated/iterated from

the Perturbation phase. The resulting walk is a case of

a stochastic search in local optimal solution space of

the problem. In Figure 1, we describe the pseudo code

of the algorithm.

1. s =GenerateInitialSolution;

2. s =LocalSearch(s );

3. Repeat

3.1. s =Perturbation(s ,history);

3.2. s =LocalSearch(s );

3.3. s =AcceptanceCriterion(s ,s ,

history);

4. Until TerminationCondition met;

5. Output s . End.

Figure 1: Iterated Local Search Method.

As you can see, it is a very simple and elegant

method that can be applied to a large number of

optimization problems, since for most of these ones

an initial solution, local search and perturbation

method can be easily defined. In practice, much of the

potential complexity of ILS is hidden in the history

dependence and in particular in the Perturbation

phase design as we will explain later. If no

dependence on the past search is used, the walk has

no memory: the perturbation and acceptance criterion

do not depend on any of the solutions visited

previously during the walk, and one accepts or not

with a fixed rule. This leads to random walk dynamics

on solution space that are “Markovian”. Most of the

work using ILS has been of this type, though recent

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

studies show that incorporating memory enhances

performance (Ramalhinho Lourenço et al. 2019).

Next, we explain in detail how to implement an

ILS method to solve optimization problems. In each

of the following sections, we will present an

extension of the ILS and one application.

2.1 Implementation Details

A general description of a metaheuristic can be seen

as a methodological approach for designing

(problem-specific) heuristics. It is preferable that a

metaheuristic to be simple, both conceptually and in

practice. But of course, it should also be effective, i.e.

it should generate very good solution in short

computational time. Most of the heuristics are

measured against accuracy, the degree of departure of

the obtained solution value from the optimal value,

and against speed, the computation time. However,

two also important attributes of the metaheuristics are

the simplicity and flexibility (Cordeau et al. 2002).

The simplicity is related with the number of

parameters to be set and facility to be implemented,

which are very few in the case of ILS. The flexibility

is related with the possibility to accommodate new

side constraints and adaptation to similar problems,

which is also quite simple to implement in a ILS

algorithm.

The ILS algorithm is composed by four main

components: GenerateInitialSolution, LocalSearch,

Perturbation, and AcceptanceCriterion. A simple

implementation of the ILS for a COP can be quite

straight-forward to design. The four main

components can be defined as follows:

(i) GenerateInitialSolution: a random feasible

solution;

(ii) LocalSearch: for most problems a local search

algorithm is readily available; Just need to

define the Neighborhood structure.

(iii) Perturbation: a random move in a higher-order

neighborhood than the one used by the local

search algorithm can be surprisingly effective;

(iv) AcceptanceCriterion: a reasonable first guess

for the acceptance criterion is to force the cost

to decrease, corresponding to a first-

improvement descent.

Basic ILS implementations of this type usually

lead too much better performance than random restart

approaches. The developer can then run this basic ILS

to build his/her intuition and try to improve the

overall algorithm performance by improving each of

the four modules and tuning their interaction.

The next step to improve the performance of the

metaheuristic is to introduce some complexity and

problem-related properties in the design of the four

components of the ILS. Next, we will describe the

main issues that it should be considered for the

improvement of the four components of the

algorithm, and comment on their interaction.

GenerateInitialSolution: Random solutions tend

to be of very low quality. Therefore, if very high-

quality solutions are to be reached by the local search,

then starting from a best possible solution becomes an

important issue. One good option is to apply a greedy

heuristic. For most of the COPs it exists a greedy

heuristic or it can easily define. Greedy solutions are

in general of higher quality than random solutions.

Other options are also available, like we will explain

latter in the hybrid ILS, other metaheuristics or even

approximation methods can be used to obtain the

initial solution. A good initial solution does not

guarantee a good final local optimal solution, but in

general it can help to reduce the search time.

LocalSearch: The overall performance of the ILS

is highly related with the choice of the local search

method, since this is one of the main components of

the method. One might think that the better the local

search, the better the corresponding ILS but if too

much time is spent in the LocalSearch phase, it is not

really an ILS but more like an extended local search.

The equilibrium between the LocalSearch phase and

the number of iterations is a main issue when

designing an ILS. It might be probably more effective

to apply a faster and more frequently local search

algorithm than a slower and more powerful one

(Stützle & Roos 2002). Therefore, the design of the

LocalSearch phase should be carefully done and the

interaction with the other components of the ILS

should be carefully considered and studied.

Perturbation: The main goal of this phase is to

escape from local optimal solution area by applying

perturbations or changes in the current local optimal

solution. An important decision is how strong the

perturbations should be. If they are too small, one will

often fall back to the previous local optimal solution

and therefore very few new solutions or a small

region of the solution space will be explored. On the

other way, if the perturbations are too big, it will be

almost like a random search, and we will end up

having a random restart type algorithm. The most

important issue to take into consideration when

designing the perturbation phase is to guarantee that

the obtained solution will not be directly undoable by

Iterated Local Search: Applications and Extensions

the local search and but should complement it in some

way. The solution obtained by the perturbation should

have a relatively different structure from the actual

local optimal solution and should also help the search

to explore new regions of the solution space. Not

necessarily this solution should be of great quality,

i.e. small cost in the minimization problem. The

design of the Perturbation phase is one of the most

important issue when implemented an ILS algorithm.

Small perturbation can lead to large computational

times and a random restart type algorithm, and large

perturbation can lead to jumping from a solution to

another without descent to a good local optimal

solution. We also recommend that the Perturbation

phase should be problem-dependent and they could

be complex perturbations as for example the

application of exact algorithms to solve subproblems

or relaxation models of the optimization problem in

consideration (Ramalhinho Lourenço 1995).

Acceptance Criterion: This procedure

determines whether is accepted or not the solution

just obtained as the new current solution.

AcceptanceCriterion has a strong influence on the

nature and effectiveness of the search in the solution

space. In a way, together with Perturbation, the

procedure controls the balance between

intensification and diversification of the search. We

can consider two strategies: a first improvement type

descent which only accepts better solutions; or at the

opposite extreme, one can always accept the new

solution irrespective of its cost. Many intermediate

choices between these two extreme cases are

possible, and in particular rather complex acceptance

criteria that involve limited amount of directed

diversification or intensification are also possible

(Stützle & Roos 2002).

After all, to improve the performance of the ILS

it should be taken into account the interactions

between the four components. Next, we briefly

mention some guidelines and suggestions that should

be considered:

 The perturbation should not be easily undone by

the local search; if the local search has obvious

shortcomings, a good perturbation should

compensate for them. The idea is that the

perturbation modifications should be of different

nature of the ones in the neighborhood and change

considerably the structure of the solution even at

the cost of worst the quality of the solution.

 The iteration between Perturbation and

Acceptance Criterion determines the relative

balance of intensification and diversification and

should receive a particularly strong attention.

Large perturbations are only useful if they can be

accepted, and that occurs only if the acceptance

criterion is not too biased towards better solutions.

 LocalSearch should be as powerful as possible as

but also not too costly in CPU time. Then, given a

choice for that module, find a well-adapted

perturbation. The equilibrium between

LocalSearch and Perturbation is really important

to study.

 Finally, define the AcceptanceCriterion procedure

so that solution space is sampled adequately.

As a final suggestion, the construction of an ILS

algorithm should start by implement a simple version

and increase complexity as needed to improve the

performance of the algorithm. One way to improve

this performance is to optimize each module

assuming the others are fixed; this is a “local

optimization” approach to the global optimization

problem. When performing such optimizations, the

interactions between the modules are essential, and

for instance the balance between intensification and

diversification is very important and remains a

challenging problem.

For a more detailed description of the ILS

algorithm see the following references: (Lourenço et

al. 2010; Lourenço et al. 2003; Ramalhinho Lourenço

et al. 2019).

Next, we will describe some history related with

the development of the ILS, followed by some

applications of ILS to several COPs.

2.2 Some History

The Iterated Local Search algorithm appeared in the

literature with several names until it was settled as

ILS as it is known today. Some are the following

ones:

 Large Step Markov Chains

 Chained Local Optimization

 Iterated Descent

 Iterated Lin-Kernighan

 Local Search with Perturbation

 Iterated Greedy Algorithm

 Iterated Local Search

One of the main and first references to ILS was

(Martin et al. 1991) with the name of Large-Step

Markov Chains. Before, there were references to

similar algorithms that maybe can considered within

the structure of ILS, which were: (Baxter 1996),

(Baum 1986) and (Johnson 1990). (Lourenço 1993)

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

extended the ILS method by using an hybrid ILS with

other metaheuristics and exact methods and applied it

to job-shop scheduling problem. Just a few years

later, T. Stützle applied it to flow-shop scheduling

problems, (Stützle 1998), and as far as we know this

was the first time that the name ILS appeared in the

literature. In the following years, many authors

contribute to the development of the ILS. Actually,

the name Iterated Local Search (ILS) is accepted all

over the research community and for a recent and

complete survey, the readers are referred to

(Ramalhinho Lourenço et al. 2019).

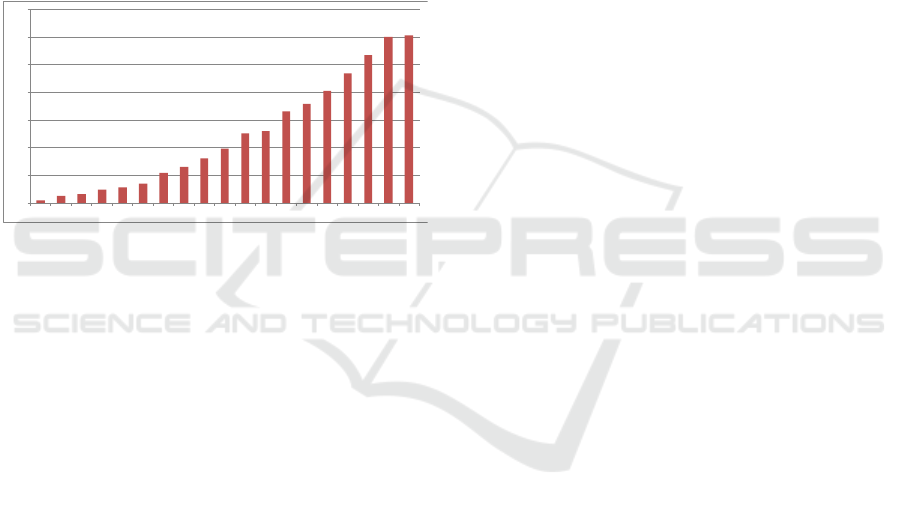
We performed a search on google scholar to have

an idea of the application of the ILS, and we found

out that the application of ILS has been steadily

increasing in the last years as shown in Figure 2.

Figure 2: Number of publications in the Google Scholar

(search done in January 2019).

2.3 Application 1: The Cut-Clique

Problem

The first example of application that we would like to

present is the development of an iterated local search

heuristics to solve the maximum cut-clique problem

published in (Martins et al. 2015). The problem

consists in finding the maximum cut-clique of a

graph. Given an undirected graph G=(V,E) and a

clique C of G, the cut-clique is the set of edges

running between C and V\C, establishing the cut

(C,V\C). The maximum cut-clique in G is to find a

clique with the largest number of edges in the

neighborhood of the clique, also known as the

maximum edge-neighborhood clique. In this work,

the authors introduce an Iterated Local Search

algorithm to solve the maximum cut-clique problem.

They compare the results with the exact methods

approach and explore a new application within

marketing analysis. They provide an application

within the area of analyzing market basket problems

in the marketing area providing interesting insides

and analysis not presented before.

3 HYBRID ILS

The ILS can be extended by using other

metaheuristics in some of the phases of the ILS, as for

example in the GenerateInitialSolution or

LocalSearch phases, or even use exact methods to

solve sub- or relaxation problems in the Perturbation

phase.

Any local search-based metaheuristic approach

like tabu search, variable neighborhood search,

GRASP or simulated annealing may be used in the

LocalSearch phase and often the performance of the

algorithm increases by using a more complex method

in this phase. This type of combination can be

included in a larger area known as Hybrid

Metaheuristics, (Blum et al. 2011). One of the first

application of hybrid ILS can be found in (Lourenço

& Zwijnenburg 1996), that uses a tabu search as the

embedded heuristic in an Iterated Local Search

algorithm to solve the job-shop scheduling problem.

Another extension that leads to very good results

is the use of exact method to solve sub- or relaxed

problems during the Perturbation phase. Many

optimization problems are difficult to solve, but some

relaxation or small instances of these problems can be

solved exactly very efficiently. So, designing a

Perturbation phase by applying an exact method to

solve simple instances of the optimization problem

leads to solutions with structures orb properties that

are not easily undo in the local search phase. This

combination of exact methods and ILS is known as

MathILS and can be included in the larger area of

Matheuristics (Talbi 2013; Dumitrescu & Stützle

2003; Puchinger & Raidl 2005). One of the first

references in the literature of a MathILS can be found

on (Ramalhinho Lourenço 1995) where, in the

Perturbation phase, an exact method is applied to

solve an one-machine scheduling problem

representing a relaxation of a job-shop scheduling

problem.

3.1 Application 2: Distribution

Problem

Distribution planning is an important activity for

many companies in the area of retailing, production

etc. The cost associated with the delivery and

distribution of goods can be an important component

of the final cost of the products. The work (Coelho et

al. 2016) presents a study on a Vehicle Routing

Problem (VRP) variant inspired on a real case of a

large distribution company. In particular, they

consider a VRP with a heterogeneous fleet of vehicles

that are allowed to perform multiple trips. The

200

400

600

800

1000

1200

1400

2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018

Iterated Local Search: Applications and Extensions

problem also includes docking constraints in which

some vehicles are unable to serve some particular

customers, and a realistic objective function with

vehicles’ fixed and distance-based costs and a cost

per customer visited. They present an Iterated Local

Search based algorithm, that combines ILS, Greedy

Randomized Adaptive Search Procedure (GRASP)

and Variable Neighborhood Descent (VND)

procedures. The method was tested with real

instances, and it was able to obtain competitive and

realistic solutions that improved the company

solutions and led to significant savings in distribution

costs.

4 SIMULATIONS AND ILS

A natural extension of the Iterated Local Search

metaheuristic is to be able to study problems with

some non-deterministic or stochastic data. In real-life

most of the problems present some kind of

uncertainty; therefore, in these cases it is common to

simplify the mathematical model assuming

deterministic data to be able to solve the problem. But

this assumption turns the model into a less accurate

one that does not reflect the stochastic nature of the

real-life problem. In order to overcome this issue, the

work (Grasas et al. 2014) proposed a framework that

combines ILS and Simulation to enable the resolution

of Stochastic Optimization Problems, known as

SimILS. This methods is included in the area of

SimHeuristics (Juan et al. 2015). The proposed

algorithm is an easy-to-implement simheuristic able

to deal with stochastic COPs in a natural way. The

integration between simulation and the ILS

algorithms must be done carefully in order to avoid

incurring in prohibitive computational times due to

the simulation component.

The general SimILS framework is presented in

Figure 3 and as described, it integrates simulation at

some specific steps, resulting in a simulation-

optimization procedure capable of dealing with

stochastic COPs.

In the SimILS, the simulations are inserted after

the application of the LocalSearch phase to evaluate

the current local optimal solution in the simulation

environment. These simulations take the current

solution and a parameter indicating whether the

simulation should be run for a long or a short time,

and then obtains the corresponding simulated

objective function (cost), along with other relevant

statistics or Key Performance Indicators (KPI) to

evaluate the solution in terms of stochastic

environment. Also, these statistics or KPI can be used

later to improve the search by updating the

LocalSearch or Perturbation phases. A long

simulation component is also inserted at the end of

the ILS process to reevaluate the final solution in a

realistic environment.

1. s =GenerateInitialSolution;

2. s =LocalSearch(s );

3. (s ,cost,statistics)=

Simulation(s ,long);;

4. Repeat

4.1.s =Perturbation(s ,history);

4.2.s =LocalSearch(s );

4.3.(s ,cost,statistics)=

Simulation(s ,short);

s =AcceptanceCriterion(s ,s ,

history);

5. Until TerminationCondition met;

6. (s ,cost,statistics)=

Simulation(s ,long);

7. Output s . End.

Figure 3: General SimILS Method.

The “simplicity” of the ILS combined with

Simulation makes this method a good alternative to

solve very complex and large-scale Stochastic

Combinatorial Optimization Problems. Some

applications can be found in: (Pagès-Bernaus et al.

2017; De Armas et al. 2017; Quintero-Araujo et al.

2017; Juan et al. 2011; Juan et al. 2014; Juan et al.

2013).

4.1 Application 3: Designing a Supply

Chain

The design of a supply chain is a relevant problem for

many industries and in particular for the retailing one.

Many references can be found in Supply Chain

Design or Location Theory. But very few studies

consider the e-commerce within the supply chain

design. E-commerce activities present characteristics

that are different from those related to traditional

retailing business. The work of (Pagès-Bernaus et al.

2017) presents two facility-location models to

represent supply chains in e-commerce. The proposed

optimization models consider stochastic demands as

well as a restricted number of regular suppliers per

customer. They also propose two solving

methodologies; the first one is a two-stage Stochastic

Programming Approach that solve a Deterministic

Equivalent Model using CPLEX. However, this

approach has several limitations to solve large-scale

instances due to the significant computational effort

required. They then propose a SimILS algorithm that

is able to solve large-scale instances in short

computing times. The proposed models and

algorithms are illustrated and tested using a set of

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

benchmark instances. Results show that better

designs can be obtained with the proposed models

and solving methodologies, and the SimILS is able to

solve efficiently large-scale instances.

5 MULTIOBJECTIVE ILS

The last extensions of ILS that we would like to

mention are the Multi-Objective Iterated Local

Search (MoILS) for (deterministic) multiobjective

problem and the Multi-objective Simulated Iterated

Local Search (MoSimILS) for multiobjective

stochastic problems.

In the case of the application of metaheuristics to

multiobjective (deterministic) problems, the

objective is to find the approximation of the Pareto

frontier and this method is included in the area of

Multiobjective Metaheuristics (Gandibleux et al.

2004).

As proposed in (Ehrgott & Gandibleux 2000), the

main idea of mutiobjective local search methods is to

consider a weighted sum of the objective functions to

search for an approximation of the nondominated

frontier. This local aggregation of the objectives

produces the effect to focus the search on a part of the

nondominated frontier. Then the weighted are

updated and the search is repeated to approximate

completely the nondominated frontier.

As the algorithms are extensions of Iterated Local

Search, all phases of the ILS and SimILS have to be

defined when a specific optimization problem has to

be solved. In the multiobjective case, the ILS will

output a pool of approximate Pareto Optimal

solutions. It is important to incorporate the

multiobjective and stochastic aspects in the definition

of the different phases of the extended ILS

algorithms. For example, the weights in the

aggregation of the objectives can help to drive the

search in a direction or other, and the statistics

obtained by the simulation can help to define that

weights. This is still an ongoing work, and in the near

future it is expected to have more applications of

these methods.

5.1 Application 4: Home Health Care

Home Health Care (HHC) service consists of

assistance provided by medical personal, such as

nurses, physical therapists and home care aides, to

people with special needs, for example old adults,

chronically ills or disabled people. The main criteria

to evaluate an HHC service solution are basically the

following ones: the service quality and the service

cost. The quality of life perceived by patients who

stays home is higher than if they stay at the hospital.

Also, a patient in a hospital has a high cost to the

community. Therefore, the benefit of the Home

Health Care service is the significant decrease in the

hospitalization rate that leads to a cost reduction in

the whole health system for one side, and the

perception of a better quality from the patient on the

other side.

During the last decade the Health Care service

industries experienced significant growth in many

European countries due to the governmental pressure

to reduce healthcare costs, the demographic changes

and the development of new services and

technologies. Therefore, a set of new optimization

problems arise that need to be solved inefficiently

(Rais & Viana 2010; Oberscheider & Hirsch 2016).

Home Health Care Problem (HHCP) consist in

defining the medical assistance route considering all

human resources constraints, working time limit and

all medical constraints. The main objectives are to

minimize the costs, the maximization of loyalty

between the medical personal and patient and, the

balance of workload between the medical personal.

The service time and transportation time is stochastic,

so the problem turns out to me a multiobjective

stochastic problem. (Galvani & Ramalhinho 2019)

studied this problem and propose a MoSimILS to

solve it. They also present the application of the

method to solve a realistic problem in Italy.

6 CONCLUSIONS

ILS has many of the most desirable features of a

metaheuristic: it is simple, easy to implement, robust,

and highly effective. The essential idea of ILS lies in

focusing the search not on the full space of solutions

but on a smaller subspace defined by the solutions

that are locally optimal for a given optimization

objective function. The efficiency of this method

depends on the design of the four main components

of the method: GenerateInitialSolution, LocalSearch,

Perturbation, and AcceptanceCriterion. However,

even with the simplest implementations of these

parts, ILS can obtain quite good solutions. And, if

more complex components are designed, the

algorithm becomes very competitive or even a state

of the art one for many optimization problems. The

modular nature of the Iterated Local Search leads to

short development times and gives ILS an edge over

more complex metaheuristics in the world of

industrial applications. We present briefly some

Iterated Local Search: Applications and Extensions

applications to exemplify the potential of the ILS

metaheuristic.

Finally, we also review some of the most relevant

extensions of the ILS that have been developed or are

under studied to be applied to many other problems,

including stochastic and multiobjective problems.

Notice that most of the real-life problems present

these two characteristics. There are still too many

questions that need more research in this last mention

extensions and there are definitely worth to study. For

example, the design of the MathILS is still an open

problem for many optimization problems. Also, the

study of MoILS and MoSimILS is still relatively new

and it requires a deeper study and more applications.

ACKNOWLEDGEMENTS

I would like to thank Thomas Stützle, Oliver Martin

and Angel Juan for all the work done in Iterated Local

Search along these years. I also would like to thank

the organization of the ICORES 2019, and in

particular to Marc Demange, for the opportunity to

present this work. And finally, none of this research

work could have been done without the amazing

support of Victor, Vera and Bruno.

REFERENCES

De Armas, J. et al., 2017. Solving the deterministic and

stochastic uncapacitated facility location problem:

From a heuristic to a simheuristic. Journal of the

Operational Research Society, 68(10), pp.1161–1176.

Baum, E.B., 1986. Towards practical “neural” computation

for combinatorial optimization problems. In J. Denker,

ed. Neural Networks for Computing, AIP conference

proceedings.

Baxter, J., 1996. Local optima avoidance in depot location.

Journal of the Operational Research Society, 32,

pp.125–133.

Blum, C. et al., 2011. Hybrid metaheuristics in

combinatorial optimization: A survey. Applied Soft

Computing, 11(6), pp.4135–4151. Available at:

http://linkinghub.elsevier.com/retrieve/pii/S15684946

11000962 [Accessed February 21, 2014].

Coelho, V.N.N. et al., 2016. An ILS-based algorithm to

solve a large-scale real heterogeneous fleet VRP with

multi-trips and docking constraints. European Journal

of Operational Research, 250(2), pp.367–376.

Available at:

http://dx.doi.org/10.1016/j.ejor.2015.09.047.

Cordeau, J.F. et al., 2002. A guide to vehicle routing

heuristics. Journal of the Operational Research

Society, 53, pp.512–522.

Dumitrescu, I. & Stützle, T., 2003. A survey of methods

that combine local search and exact algorithms.

Applications of Evolutionary Computation, (i), pp.211–

223.

Ehrgott, M. & Gandibleux, X., 2000. A survey and

annotated bibliography of multiobjective combinatorial

optimization. OR Spectrum, 22(4), pp.425–460.

Available at:

http://link.springer.com/10.1007/s002910000046.

Galvani, M. & Ramalhinho, H., 2019. An Iterated Local

Search approach to solve multi-objective and

stochastic Home Health Care Problem, Barcelona,

Spain.

Gandibleux, X. et al., 2004. Metaheuristics for

Multiobjective Optimisation Lecture No. Springer, ed.,

Grasas, A., Juan, A.A.A.A. & Lourenço, H.R.H.R., 2014.

SimILS: a simulation-based extension of the iterated

local search metaheuristic for stochastic combinatorial

optimization. Journal of Simulation, 10(1), pp.1–9.

Available at:

http://www.scopus.com/inward/record.url?eid=2-s2.0-

84961324333&partnerID=tZOtx3y1 [Accessed

November 5, 2014].

Johnson, D.S., 1990. Local optimization and the Traveling

Salesman Problem. In M. S. Paterson, ed. Automata,

Languages and Programming. Berlin, Heidelberg:

Springer Berlin Heidelberg, pp. 446–461.

Juan, A.A. et al., 2015. A review of simheuristics:

Extending metaheuristics to deal with stochastic

combinatorial optimization problems. Operations

Research Perspectives, 2(1), pp.62–72. Available at:

http://linkinghub.elsevier.com/retrieve/pii/S22147160

1500007X.

Juan, A.A. et al., 2014. A simheuristic algorithm for the

Single-Period Stochastic Inventory-Routing Problem

with stock-outs. Simulation Modelling Practice and

Theory, 46, pp.40–52.

Juan, A.A. et al., 2013. Using parallel and distributed

computing for solving real-time Vehicle Routing

Problems with Stochastic Demands. Annals of

Operations Research, 2017(1), pp.43–65.

Juan, A.A. et al., 2011. Using safety stocks and simulation

to solve the vehicle routing problem with stochastic

demands. Transportation Research Part C: Emerging

Technologies, 19(5), pp.751–765. Available at:

http://linkinghub.elsevier.com/retrieve/pii/S0968090X

10001439 [Accessed July 25, 2014].

Lourenço, H.R., 1993. A computational study of job shop

and the flow shop scheduling problems. Cornell

UNiversity.

Lourenço, H.R. et al., 2003. Iterated local search. In F.

Glover & G. Kochenberger, eds. Handbook of

Metaheuristics. Kluwer Academic, pp. 321–353.

Lourenço, H.R., Martin, O. & Stützle, T., 2010. Iterated

Local Search: Framework and Applications. In M.

Gendreau & J. Y. Potvin, eds. Handbook of

Metaheuristics. New York, New York, USA: Springer,

pp. 363–397.

Lourenço, H.R. & Zwijnenburg, M., 1996. Combining the

large-step optimization with tabu-search : application to

the job-shop scheduling problem. In I. H. Osman & J.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

P. Kelly, eds. Meta-Heuristics: Theory and

Applications. Kluwer Academic Publishers, pp. 219–

236.

Martí, R., Panos, P. & Resende, M.G.C., 2018. Handbook

of Heuristics, Springer, Cham.

Martí, R., Resende, M.G.C.C. & Ribeiro, C.C., 2013.

Multi-start methods for combinatorial optimization.

European Journal of Operational Research, 226(1),

pp.1–8. Available at: http://linkinghub.elsevier.com/

retrieve/pii/S0377221712007394 [Accessed March 14,

2014].

Martin, O., S.W., O. & Felten, E.W., 1991. Large-Step

Markov Chains for the Traveling Salesman Problem.

Complex Systems, 5, pp.299–326.

Martins, P., Ladrón, A. & Ramalhinho, H., 2015. Maximum

cut-clique problem: ILS heuristics and a data analysis

application. International Transactions in Operational

Research, 22(5), pp.775–809. Available at:

http://doi.wiley.com/10.1111/itor.12120 [Accessed

September 23, 2014].

Oberscheider, M. & Hirsch, P., 2016. Analysis of the

impact of different service levels on the workload of an

ambulance service provider. , 16(1).

Pagès-Bernaus, A. et al., 2017. Designing e-commerce

supply chains: A stochastic facility-location approach.

International Transactions in Operational Research.

Puchinger, J. & Raidl, G.R., 2005. Combining

Metaheuristics and Exact Algorithms in Combinatorial

Optimization: A Survey and Classification. Lecture

Notes in Computer Science, 3562.

Quintero-Araujo, C.L. et al., 2017. Using simheuristics to

promote horizontal collaboration in stochastic city

logistics. Progress in Artificial Intelligence, 6(4),

pp.275–284. Available at: http://link.springer.com/

10.1007/s13748-017-0122-8.

Rais, A. & Viana, A., 2010. Operations Research in

Healthcare: a survey. International Transactions in

Operational Research, 18(1), pp.1–31. Available at:

http://doi.wiley.com/10.1111/j.1475-

3995.2010.00767.x [Accessed January 22, 2014].

Ramalhinho Lourenço, H., 1995. Job-Shop Scheduling:

computational study of local search and large-step

optimization methods. European Journal of

Operational Research, 83, pp.347–364.

Ramalhinho Lourenço, H., Martin, O. & Stützle, T., 2019.

Iterated Local Search: Framework and Applications. In

M. Gendreau & J. Y. Potvin, eds. Handbook of

Metaheuristics. Springer International Publishing.

Stützle, T., 1998. Applying iterated local search to the

permutation flow shop problem,

Stützle, T. & Roos, H.H., 2002. Analyzing the run-time

behaviour of iterated local search for TSP. In P. Hansen

& C. Ribeiro, eds. Essays and Surveys in

Metaheuristics. Kluwer Academic Publishers, pp. 589–

612.

Talbi, E.G., 2013. Combining metaheuristics with

mathematical programming, constraint programming

and machine learning. 4or, 11(2), pp.101–150.

BRIEF BIOGRAPHY

Helena Ramalhinho Lourenço is a Full Professor at

the Economics and Business Department at the

University Pompeu Fabra, Barcelona, Spain. She has

a B.A. and Master degree in Statistics and Operations

Research from the University of Lisbon, Portugal,

and a Ph.D. in Operations Research from Cornell

University, New York, USA. She has been involved

in different research projects and consulting for firms

in the area of Operations Research and Logistics.

Helena has published several articles in prestigious

international scientific journals and has presented her

work at international congresses and conferences.

Helena teaches at various undergraduate, master’s

and PhD`s programs. She is currently the director of

the Business Analytics Research Group and a

researcher at the Center for Operational Research at

the University of Lisbon. Her research interests

include Operations Research, Scheduling,

Combinatorial Optimization, Metaheuristics, Iterated

Local Search, Heuristic Search Optimization, Vehicle

Routing, Job-Shop Scheduling, Supply Chain

Management, Logistics, Production and Operations

Management.

Iterated Local Search: Applications and Extensions