
Model-based Integration of Unstructured Web Data Sources using
Graph Representation of Document Contents
Radek Burget
a
Faculty of Information Technology, Brno University of Technology, Bozetechova 2, Brno, Czech Republic
Keywords:
Information Integration, Domain Modelling, Document Processing, Structured Record Extraction.
Abstract:
Unstructured or semi-structured documents on the web are often used as a media for publishing structured,
domain-specific data which is not available from other sources. Integration of such documents as a data
source to a standard information system is still a challenging problem because of the very loose structure of
the input documents and usually missing semantic annotation of the published data. In this paper, we propose
an approach to data integration that exploits the domain model of the target information system. First, we
propose a graph-based model of the input document that allows to interpret the contained data in different
alternative ways. Further, we propose a method of aligning the document model with the target domain model
by evaluating all possible mappings between the two models. Finally, we demonstrate the applicability of the
proposed approach on a sample domain of public transportation timetables and we present the preliminary
results achieved with real-world documents available on the web.
1 INTRODUCTION
Despite much effort dedicated to the development of
different technical means for annotating the semantics
of the presented data such as Microformats
1
, RDFa
2
and others, the World Wide Web is still an extremely
large source of mostly unannotated documents. These
documents often contain structured and potentially
useful data presented in a way that is convenient for
human readers but it is completely unsuitable for au-
tomated processing. Therefore, using the documents
as a data source for traditional information systems
that are based on structured data models presents a
challenging task.
A typical domain-oriented information system
uses a structured data representation and storage (for
example a relational database), which has been de-
signed based on the analysis of the target domain,
identification of the individual entities, their proper-
ties and the relationships among them. However, on
the web, many potential sources of domain-specific
data have the form of documents designed primarily
for human readers. Although the data contained in
these documents follow basically the same structure
that comes from the target domain, their integration
a
https://orcid.org/0000-0001-5233-0456
1
https://microformats.io/
2
https://rdfa.info/
to an existing information system is difficult because
of the very loose way of their presentation without
any formal annotation.
In (Burget, 2017), we have mentioned several
domains, where this situation is quite typical such
as scholarly data (conference proceedings contents),
sports results or public transport time tables. In all
these (and many other) domains, the data has a fixed
and predictable structure that potentially allows its
integration to existing applications in the respective
domains. However, the corresponding data sources
often have the form of periodically published docu-
ments (mostly web pages; PDF documents are typical
for some domains such as timetables) whose human
interpretation is assumed for understanding the pre-
sented data.
Traditionally, the integration of such web sources
is implemented using different kinds of wrappers
that recognize data fields in the documents by an-
alyzing the underlying document code – mostly
the HTML code represented as a Document Object
Model (DOM) (Schulz et al., 2016). For each data
source (the source of the input documents), the corre-
sponding code patterns are different and therefore, a
specific wrapper must be prepared. Such approach is
reliable and feasible when considering a limited num-
ber of previously known data sources that provide a
larger number of documents but it is not practical at
326
Burget, R.
Model-based Integration of Unstructured Web Data Sources using Graph Representation of Document Contents.
DOI: 10.5220/0008350103260333
In Proceedings of the 15th International Conference on Web Information Systems and Technologies (WEBIST 2019), pages 326-333
ISBN: 978-989-758-386-5
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

all, when the input documents come from previously
unknown sources, each document has been prepared
independently and uses a completely different way of
data presentation.
In this paper, we propose a model-based approach
aiming to overcome the specific details of the in-
dividual documents by an automatic discovery of a
mapping between the previously defined domain data
model and the presented data records. The main pre-
sented contributions are the following:
• We present a technology- and language-
independent graph-based model of the document
contents that allows to interpret the contained
data in different alternative ways.
• We propose a method for evaluating the possible
mappings between the created document model
and the target domain model that describes the
expected structure of the contained data and for
choosing the best mapping based on a statistical
analysis.
• We demonstrate the application of the described
approach on a sample domain of public transport
timetables.
We also include preliminary results of this work in
progress that show the applicability of the proposed
document model and mapping methods on real-world
documents.
2 RELATED WORK
The research in the topic of data record extraction
from web documents has been running for over 20
years. Apart from historical HTML-based approaches
(Schulz et al., 2016), due to the evolution of the web
technology (mainly in the HTML and CSS languages
and the dynamic web pages) and the increasing com-
plexity of web documents, the recent approaches usu-
ally combine the analysis of the document code, with
visual presentation properties (Potvin and Villemaire,
2019; Shi et al., 2015). However, most of the cur-
rent methods use DOM
3
as the primary document
representation (Figueiredo et al., 2017; Guo et al.,
2019; Lockard et al., 2018; Shi et al., 2015; Yu-
liana and Chang, 2018). This limits the applicability
of the methods to specific HTML documents where
the DOM elements accurately delimit the desired data
fields.
From the data integration point of view, the cur-
rent methods infer the schema of the extracted records
from the source documents themselves (Figueiredo
3
https://www.w3.org/DOM/
et al., 2017; Shi et al., 2015; Yuliana and Chang,
2018). In all cases, the approach is to find a specific
region or multiple regions (Figueiredo et al., 2017)
that contain the records and then, a flat internal struc-
ture of the records is determined based on finding the
regular patterns in the document code and by com-
paring the similarity and other characteristics of the
repeating sequences. This approach allows easy ap-
plication of the methods to any document indepen-
dently on its domain; however, the integration of the
extracted data to a domain information system re-
quires further interpretation and transformation of the
extracted records.
In contrast to the above mentioned data-driven ap-
proaches, there has been significantly less attention
given to the research of the model-driven approaches.
(Embley et al., 1999) uses a conceptual domain model
that is directly mapped to HTML code based on dif-
ferent heuristics. In (Potvin and Villemaire, 2019) a
flat list of extracted data field is used and (Lockard
et al., 2018) integrates the extracted data with an ex-
isting knowledge base.
In our previous research (Burget, 2017), we have
proposed a basic approach for matching individual bi-
nary relationships in a domain model to visual pre-
sentation patterns in the documents. In this paper, we
generalize the matching to the whole domain mod-
els and above all, we introduce a formal graph-based
document model of the input documents that makes
the matching possible.
3 THE DATA INTEGRATION
TASK
The data integration task we consider in this paper
is the following: We have a (potentially unlimited)
collection of unstructured input documents on the
source side and a structured domain-specific informa-
tion system on the target side.
The target information system is typically de-
signed based on the analysis of the particular domain,
which results in a domain data model such as a entity-
relationship diagram (ERD) or its equivalent depend-
ing on the used design methodology. The model cap-
tures the basic entity sets, their properties (attributes)
and the relationships among them. Independently on
whether an ERD or another formalism is used, we
may define a domain model for our purpose as fol-
lows:
Definition 1. A domain model is a tuple D = (E, P, R),
where E is a set of entity sets, P is a set of properties
(attributes in ERD) and R ⊂ (E × (E ∪ P)) is the set
of relationships.
Model-based Integration of Unstructured Web Data Sources using Graph Representation of Document Contents
327

Figure 1 shows a simple ERD for the public trans-
port timetables domain. Note that we consider just a
part of the ERD that is relevant to the considered data
sources; the complete ERD for a real-world informa-
tion system would be obviously significantly larger.
Figure 1: An entity-relationship model for the domain of
public transportation timetables with two entity sets (Time,
Stop), three properties (Hour, Minute, Name) and one rela-
tionship (stops at).
At the input, we assume a collection of documents
that contain visually presented structured data records
consisting of several data fields. The documents come
generally from different sources and therefore, the
way of data presentation, formatting or the implemen-
tation may be different for every single document.
However, we put the following assumptions on the
input documents:
• We assume formatted text documents where the
document creator may specify the visual proper-
ties (fonts, colors, etc.) for every part of the docu-
ment text as well as the visual organization of the
contents (alignment, spacing, etc.) by any means.
For the web sources, the HTML web pages and
PDF documents are the most typical but our con-
tent model presented below in section 4 is inde-
pendent on the actual technology.
• Every document contains multiple data records
consisting of the data fields that may be directly
mapped to the properties in the target ERD (i.e.
without any additional transformations) and the
records are consistent regarding their structure
and visual presentation (their visual properties
and organization as mentioned above).
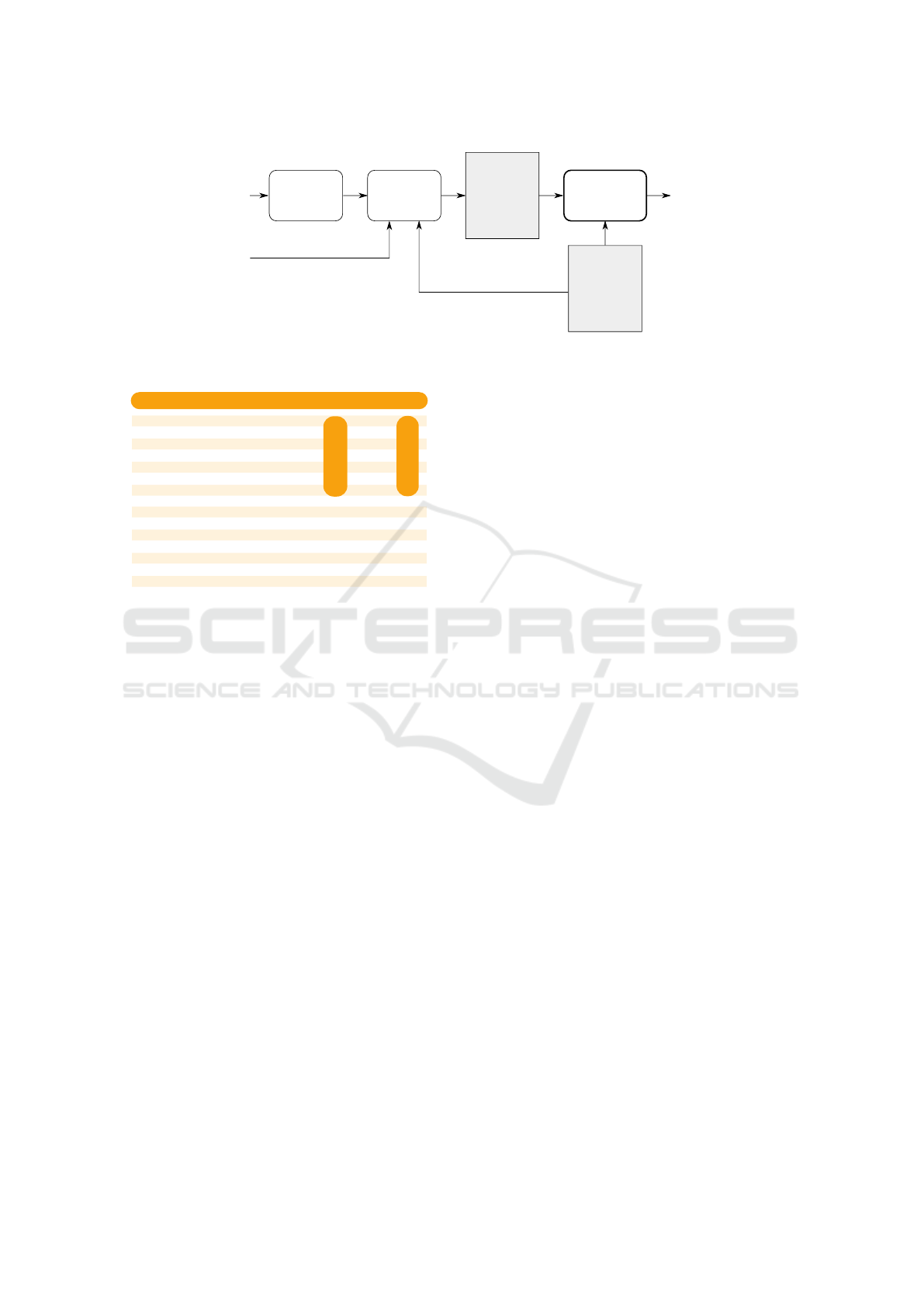
Figure 2 gives the overview of the document pro-
cessing process. First, the visual properties and posi-
tions of all parts of the document text are computed.
This is the only task that depends on the document
type. For some document types such as HTML, this
requires rendering the document by a web browser. In
PDF documents, the necessary information is avail-
able directly. In the next steps, we identify the text
chunks that represent the candidate substrings of the
document text that potentially could represent a data
field. Based on the extracted text chunks, we build
a page contents model, which is basically a graph
that describes the visual properties of the individ-
ual chunks and the visually presented relationships
among them. We describe the model and its construc-
tion below in section 4.
The key part of the information integration pro-
cess consists of finding the most appropriate mapping
between the created document contents graph and the
domain model. For this purpose, we also represent
the domain model as a graph of the entity properties
and the relationships among them and we search for a
best mapping between the two graphs. The details of
this process are described in section 5.
In the following sections, we will use the already
mentioned public transport timetables as a sample do-
main. Our goal is to integrate the data about the stops
and the corresponding times from the timetable docu-
ments as shown in Figure 1. We believe, this domain
is suitable for illustrating the individual steps for the
following reasons:
• It is challenging. The timetables are a good exam-
ple of source documents that present data in a very
ambiguous way and even the human readers need
some experience to interpret the data properly in
some more complex cases.
• It is practically useful. Although there exist differ-
ent portals and aggregators in this domain, they
are usually limited to certain countries, regions
or groups of companies and they typically do not
provide their structured data to third parties.
• There are many highly diverse documents from
different transportation companies available on
the web.
However, the presented integration approach is
not limited to a single domain as long as the above
mentioned assumptions on the input documents are
met.
4 DOCUMENT CONTENTS
MODEL
The goal of the proposed document contents model is
to capture the possibly relevant parts of the document
contents and their mutual relationships based on their
visual presentation. We define the model as a graph:
Definition 2. The document contents model is defined
as a graph G = (C, E), where C is a set of text chunks
WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies
328
Page
rendering
Presentation to
domain model
mapping
HTML
documents
Text chunk
extraction
PDF
documents
Text boxes
Page contents
model
(graph)
Structured
data records
Domain
model
Attributes (properties)
Figure 2: An overview of the data integration process.
Lincoln | County Hospital
Monday to Satu rday except Bank Holidays
Lincoln Bus Station 0700 0720 0745 15 45
Monks Road 12 0710 0730 0755 25 55
Tower Estate 0712 0732 0757 27 57
County Hospital 0719 0739 0805 35 05
Tower Estate 0722 0742 0808 38 08
Monks Road 12 0725 0745 0811 41 11
Lincoln Bus Station 0740 0800 0825 55 25
Lincoln Bus Station 1545 1620 1650 1720 1750
Monks Road 12 1555 1630 1700 1730 1800
Tower Estate 1557 1632 1702 1732 1802
County Hospital 1605 1640 1710 1740 1810
Tower Estate 1608 1643 1713 1743 1813
Monks Road 12 1611 1646 1716 1746 1816
Lincoln Bus Station 1625 1700 1730 1800 1830
for Sunday journeys see line 17 & 18 timetables
then every
30 mins
until
Figure 3: An example time table.
that represent the relevant parts of the contents to-
gether with their visual formatting and form the ver-
tices of the graph; E ⊂ C ×C is a set of graph edges,
that represent the relationships among the chunks as
expressed by the document layout.
With a text chunk, we understand any piece of
content (a substring of the document text), that pos-
sibly represents a value of a domain property. In the
moment of the chunk extraction, we do not decide,
whether the given substring really represents a part of
a data record; the goal is to identify all substrings that
“look like” a value of a given property when consid-
ered separately.
Definition 3. A text chunk is a tuple c = (t
c
, s
c
, p
c
),
where t
c
is the text of the chunk (the actual substring
of the document text), s
c
represents the visual style of
the text and p
c
represents the position of the chunk as
displayed in the resulting page.
Definition 4. The chunk style is further defined as
s
c
= ( f s, w, st, c, bc) where f s is the average font size,
w ∈ [0, 1] is the average font weight from 0 (normal
font) to 1 (bold font), st ∈ [0, 1] is the average font
style (1 for italic font, 0 for regular font) and c and bc
are the computed foreground and background colors
of the displayed chunk.
Definition 5. The position p
c
= (x, y, w, h) describes
the x and y coordinates of the chunk in the page and
its width w and height h.
The edges E of the graph represent the mutual re-
lationships among the chunk pairs. Based on their
mutual positions, we identify specific relationships
that are interesting for further analysis of the whole
data record organization. For example, two chunks
may be in a onRight, below, sameLine or another re-
lation as described in section 4.2.
Both the chunks and the relationships are ex-
tracted from rendered documents as shown in Figure
2. In the next sections, we provide the details of the
chunk and relationship extraction.
4.1 Chunk Extraction
For the chunk extraction, we use a connected line as a
smallest unit of the rendered document.
Definition 6. A connected line represents a part of
the document text that is positioned on a single line
(considering the y coordinates of the individual char-
acters) and it does not contain an empty space wider
than a certain threshold ∆x.
In our experimental setup, we have used ∆x =
2.5 f where f is the average font size used at the con-
sidered line. The goal of this setting is to ensure
that the normal text formed by space-separated words
forms single lines and the parts separated with a larger
space create separate connected lines.
Example 1. In the example timetable in Figure 3, the
header and footer text forms continuous text lines;
however, the stop names and the time data are sep-
arated by a larger space. Thus, we obtain the
connected lines “Lincoln Bus Station”, “0700 0720
0745”, “15” and “45” for the first line of the sched-
ule, etc. Note that the connected lines are not neces-
sarily consistent regarding their style; they may con-
tain text with different font weights, colors, etc. as we
may notice for the station names.
Model-based Integration of Unstructured Web Data Sources using Graph Representation of Document Contents
329

For each domain model property p ∈ P (see Def-
inition 1), we extract a set C
p
of chunks from all the
connected lines. The algorithm for the chunk discov-
ery within the connected lines depends greatly on the
type of the property p. For our sample domain, we
have used a simple algorithm that finds all one- or
two-digit numbers in the appropriate range for hours
and minutes; the chunks for stop names are discov-
ered using a simple regular expression allowing a se-
quence of alphanumeric characters and some com-
monly used punctuation. In our previous experiments
on other domains (Burget, 2017), we have also men-
tioned the usage of named entity classifiers (Finkel
et al., 2005) for recoginizing personal names and
locations or even using the DBPedia Spotlight tool
(Daiber et al., 2013) for recoginizing entities from the
DBPedia dataset. Advanced algorithms for numeric
value discovery have been proposed as well (Neu-
maier et al., 2016).
As the result of the chunk extraction, we ob-
tain a complete set of chunks for all the properties
C = C
p
1
∪ C
p
2
∪ . . . ∪ C
p
n
where n = |P|. Note that
the chunk detection itself may be quite inaccurate as
we use very approximate methods for the chunk ex-
traction. The extracted chunks may even overlap; e.g.
in the “Monks Road 12” string, we discover three
chunks: the whole string forms the name chunk, the
“12” substring forms the hour and minute chunks be-
cause both interpretations are possible. It is the task
of the mapping phase (described in section 5) to com-
plete the data records and exclude the incorrectly dis-
covered chunks.
4.2 Relationship Modelling
After the chunks have been detected, we analyze all
the chunk pairs (c
1
, c
2
) ∈ C ×C and we investigate
whether there is an relationship between c
1
and c
2
given by their mutual positions (x
1
, y
1
) and (x
2
, y
2
).
We have identified several relationships that are in-
teresting for further analysis. Every relationship is
defined by a relation E
x
⊂ C × C and we say that
there is a spatial relationship x between c
1
and c
2
iff
(c
1
, c
2
) ∈ E
x
. Currently, we consider the following
relationships:
• onRight – (c
1
, c
2
) ∈ E
onRight
when c
1
and c
2
are
placed on the same line just next to each other and
c
2
is on the right side of c
1
.
• after – c
2
is on the same line anywhere to the right
of c
1
.
• sameLine – c
1
and c
2
are on the same line regard-
less their mutual positions.
• below – c
2
is placed just below c
1
.
• lineBelow – c
2
is placed on a line that is just below
c
1
.
As we may see, a chunk pair may belong to multi-
ple relations as the spatial relationships (e.g. after and
sameLine) are not mutually exclusive.
Finally, the complete set of relationships is then
E =
S
E
x
for all the relations x listed above. Together
with the set C of chunks, it creates the document con-
tent graph as defined in Definition 2.
5 MAPPING TO THE DOMAIN
MODEL
Our information integration approach is based on the
assumption that some of the extracted text chunks
may be mapped to the individual properties of the
domain model as defined in Definition 1 and sim-
ilarly, some discovered spatial relationships among
them may be mapped to the domain model relation-
ships. During the mapping phase, we find all possi-
ble mappings from the constructed document contents
graph to the domain model, we evaluate them and fi-
nally, we use the best mapping found.
Below, we describe the representation of the do-
main model used for the final mapping. Further in
section 5.2, we define a mapping formally and finally
in section 5.3, we discuss the way of evaluating the in-
dividual mappings and finding the most suitable one.
5.1 Domain Model Transformation
As the first step, we transform the domain model to a
simplified graph model that describes only the proper-
ties and relationships as the entity sets have no direct
representation in the documents. An example model
for the timetables domain is shown in Figure 4. The
properties are divided into groups (the dashed boxes)
where each group corresponds to a set of properties
that are always presented together in a 1:1 relation-
ship.
Definition 7. The domain graph model is a graph
D
g
= (G, R
g
) where G = {G
1
, G
2
, . . . , G
n
} is a set
of property groups, G
i
⊂ P and G
i
∩ G
j
= ∅ for
any 1 ≤ i, j ≤ n. P is the set of domain properties.
R
g
⊂ G × G is a set of relationships between groups.
The domain graph is constructed from the domain
model defined in Definition 1 as follows:
• All the properties of a single entity set belong to
the same group.
• If two entity sets are in a 1:1 relationship, all their
properties belong to a single group.
WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies
330

name
(Stop)
minute
(Time)
1
n
G
1
G
2
hour
(Time)
Figure 4: A domain graph model corresponding to the do-
main model shown in Figure 1 that represents the property
groups and the relationships among them.
• The 1:M relationships are transformed to the rela-
tionships between the respective groups.
Currently, we don’t consider M:N relationships in
our method because they are difficult to represent in
the documents in an understandable way and there-
fore, they are very rarely used in source documents.
Considering the example from Figure 1, we obtain
two groups of properties: G
1
= {hour, minute} and
G
2
= {name} as shown in Figure 4. Subsequently, we
analyze the possible mappings between the document
contents graph and the domain graph model.
5.2 Mapping Representation
When considering a particular document represented
by the document contents graph, there exist many
possible mappings between the chunks and the prop-
erties in the domain graph and similarly, between the
relationships in the two graphs. In our approach, a
mapping presents a hypothesis about the visual pre-
sentation of data records, which is subsequently eval-
uated and compared with other hypotheses.
Based on the above mentioned assumption that
there exist multiple visually consistent data records in
the source documents, a mapping basically describes
two aspects of the records:
1. The visual style of the text chunks used for pre-
senting each property p ∈ P in the input docu-
ment.
2. The actual spatial relationships (as mentioned in
section 4.2) among the property values.
Let’s consider the chunk style defined in Defini-
tion 4 and let S be a set of all distinct chunk styles
used in the input document. Further, let R
s
be the set
of all spatial relationships between chunks discovered
in the input document. Then, we may define the map-
ping between a property group G
i
in the domain graph
and the document contents graph as follows:
Definition 8 (Group Mapping.). For each group G
i
∈
G, the mapping is defined as m
i
= ( f
si
, f
ri
) where f
si
:
G
i
7→ S is a morphism that assigns a chunk style to
each property in G
i
and f
ri
: G
i
× G
i
7→ R
s
assigns
spatial relationships to the property pairs.
The f
rg
morphism does not necessarily assign a re-
lationship to all possible property pairs. For a unique
description of the mapping, it is sufficient that the
property pairs form a connected graph. For example,
considering three properties a, b and c, the mapping
may contain (a, b) 7→ onRight, (a, c) 7→ below (which
can be read as b is on the right side of a and c is be-
low a). We obtain a connected graph of properties
and therefore, it is not necessary to find any relation-
ship for the remaining combinations such as (b, c).
Considering the group G
1
in Figure 4, it is sufficient
to find one of the morphisms (hour, minute) 7→ r or
(minute, hour) 7→ r, where r ∈ R
s
.
Similarly, we define an inter-group mapping that
corresponds to the way how the connection of two
groups is visually presented in the document:
Definition 9 (Inter-group Mapping.). For a pair of
groups (G
i
, G
j
) ∈ G × G, the inter-group mapping is
m
i j
= (p
i
, p
j
, r) where p
i
∈ G
i
, p
j
∈ G
j
and r ∈ R
s
.
In other words, we define a spatial relationship r
between two properties where the first property be-
longs to the first group and the second property be-
longs to the second group. Again, we have to find
enough mappings between the group pairs so that we
obtain a connected graph of groups. Then, the com-
plete mapping is m = (M
G
, M
I
) where M
G
is a set con-
taining a group mapping for each group in G and M
I
is a set of the inter-group mappings.
Example 2. When considering our example
timetable in Figure 3 and the domain graph in
Figure 4, we find many different styles used for
the presentation of the hour values in the document
(when considering the style of all the chunks in C
hour
)
and similarly for the minute and name properties (the
style morphisms f
s1
and f
s2
). Moreover, we find
different ways how the (hour, minute) pair is possibly
presented, e.g. minute is on the right side of hour or
minute is below hour or hour is below minute, etc.
(the f
ri
morphism). And finally, we find the possible
presentation of the inter-group relation, e.g. hour is
on the same line as name. Since hour and name are in
separate groups in the domain graphs, we know that
hour actually represents a complete (hour, minute)
group and there may exist multiple such pairs related
to a single name because of the 1:N relationship
between the groups.
By considering all combinations of chunk styles,
and the applicable intra-group and inter-group rela-
Model-based Integration of Unstructured Web Data Sources using Graph Representation of Document Contents
331

tionship representations, we obtain a set M of all pos-
sible mappings from the contents graph to the domain
model graph.
5.3 Evaluation of the Mappings
The last step is the evaluation all the mappings and
choosing the most suitable one. For each mapping
m ∈ M, we apply the style and spatial relationship
mappings on the document text chunks and as a re-
sult, we obtain a set of candidate data records, where
each data field of the record is represented by a text
chunk.
For the evaluation, the following aspects of the
discovered candidate records are important:
• The number of chunks actually covered by the
records. Although we admit that some of the
chunks may have been incorrectly identified, we
assume that the correctly identified ones prevail
and thus, more chunks contained in the discovered
records indicate a better result.
• Visual consistency of the records. The given map-
ping defines the actual visual style of the chunks
mapped to the individual properties as well as the
spatial relationships among them (e.g. hours and
minutes being at the same line). However, the
records may differ in the distance and alignment
of the particular chunks. When evaluating con-
sistency, we compare the individual records and
we observe the variance of the corresponding dis-
tances among the chunks. The lower the overall
variance is, the more consistent (and thus better)
are the records.
Additionally, we allow using certain number of
wildcards in style specifications. It is quite common
in visual presentation that some of the records or data
fields are distinguished from the others by a differ-
ent background color, font style, etc. In our experi-
ments, we allow one wildcard in the chunk style, i.e.
based on the style defined in Definition 4, one the
( f s, w, st, c, bc) attributes may be disregarded.
As we may notice, the two evaluation criteria
mentioned above are contradictory to some extent. It
is easy to cover a large number of chunks and dis-
cover many data records when we allow low visual
consistency of records and vice versa. For our ex-
periments we have empirically set the total mapping
score to s = 0.6p + 0.4c where p is the percentage
of chunks contained in the records and c is the visual
consistency, p, c ∈ [0..1].
6 EXPERIMENTAL EVALUATION
For the evaluation on real-world documents, we have
implemented the proposed method in Java. For in-
put document processing, we have used the CSSBox
4
rendering engine for HTML documents and the PDF-
Box
5
library for reading PDF documents.
Our preliminary tests (being this a work in
progress) were run on 30 timetables in PDF available
online on the websites of various transportation com-
panies that operate in different en countries (Czechia,
Spain, Italy and the United States). As a second use
case, we have extracted the publication data (authors,
titles and sessions) from CEUR Workshop Proceed-
ings
6
(HTML documents).
The tests have shown the practical usability of the
proposed document contents model described in sec-
tion 4 as well as the domain mapping method. How-
ever, in about 10% of input documents, the correct
mapping was not evaluated as the best one and the
evaluation function had to be adjusted for obtaining
correct results. Therefore, we consider the mapping
evaluation the main issue for our ongoing research.
7 CONCLUSIONS
In this paper, we have proposed an approach to the
integration of the data contained in web documents
to structured information systems. Unlike most of the
existing approaches that derive the data structure from
the input documents, our method is driven by a pre-
viously defined domain model of the information sys-
tem.
In order to make the information integration pos-
sible, we have designed a graph-based model of the
document contents and subsequently, we have pro-
posed a method for finding the best mapping of the
document contents model to the domain model. Our
preliminary results show that the approach allows in-
tegration of real-world HTML and PDF documents
and mapping of the published data to the fixed do-
main model. The evaluation of the possible mappings
seems to be the most challenging topic for our next
research.
4
http://cssbox.sourceforge.net
5
https://pdfbox.apache.org/
6
http://ceur-ws.org/
WEBIST 2019 - 15th International Conference on Web Information Systems and Technologies
332

ACKNOWLEDGEMENTS
This work was supported by the Ministry of the In-
terior of the Czech Republic as a part of the project
Integrated platform for analysis of digital data from
security incidents VI20172020062.
REFERENCES
Burget, R. (2017). Information extraction from the web
by matching visual presentation patterns. In Knowl-
edge Graphs and Language Technology: ISWC 2016
International Workshops: KEKI and NLP&DBpedia,
Lecture Notes in Computer Science vol. 10579, pages
10–26. Springer International Publishing.
Daiber, J., Jakob, M., Hokamp, C., and Mendes, P. N.
(2013). Improving efficiency and accuracy in mul-
tilingual entity extraction. In Proceedings of the
9th International Conference on Semantic Systems (I-
Semantics).
Embley, D. W., Campbell, D. M., Jiang, Y. S., Lid-
dle, S. W., Lonsdale, D. W., Ng, Y.-K., and Smith,
R. D. (1999). Conceptual-model-based data extrac-
tion from multiple-record web pages. Data Knowl.
Eng., 31(3):227–251.
Figueiredo, L. N. L., de Assis, G. T., and Ferreira, A. A.
(2017). Derin: A data extraction method based on
rendering information and n-gram. Information Pro-
cessing & Management, 53(5):1120 – 1138.
Finkel, J. R., Grenager, T., and Manning, C. (2005). Incor-
porating non-local information into information ex-
traction systems by gibbs sampling. In Proceedings
of the 43rd Annual Meeting on Association for Com-
putational Linguistics, ACL ’05, pages 363–370.
Guo, J., Crescenzi, V., Furche, T., Grasso, G., and Gott-
lob, G. (2019). Red: Redundancy-driven data extrac-
tion from result pages? In The World Wide Web Con-
ference, WWW ’19, pages 605–615, New York, NY,
USA. ACM.
Lockard, C., Dong, X. L., Einolghozati, A., and Shiralkar,
P. (2018). Ceres: Distantly supervised relation extrac-
tion from the semi-structured web. Proc. VLDB En-
dow., 11(10):1084–1096.
Neumaier, S., Umbrich, J., Parreira, J. X., and Polleres, A.
(2016). Multi-level semantic labelling of numerical
values. In The Semantic Web – ISWC 2016, pages
428–445, Cham. Springer International Publishing.
Potvin, B. and Villemaire, R. (2019). Robust web data ex-
traction based on unsupervised visual validation. In
Intelligent Information and Database Systems, pages
77–89, Cham. Springer International Publishing.
Schulz, A., L
¨
assig, J., and Gaedke, M. (2016). Practical web
data extraction: Are we there yet? – a short survey.
In 2016 IEEE/WIC/ACM International Conference on
Web Intelligence (WI), pages 562–567.
Shi, S., Liu, C., Shen, Y., Yuan, C., and Huang, Y.
(2015). Autorm: An effective approach for automatic
web data record mining. Knowledge-Based Systems,
89:314 – 331.
Yuliana, O. Y. and Chang, C.-H. (2018). A novel
alignment algorithm for effective web data extrac-
tion from singleton-item pages. Applied Intelligence,
48(11):4355–4370.
Model-based Integration of Unstructured Web Data Sources using Graph Representation of Document Contents
333
