Improved ADRC Controller based on Model Information and Special

Filter Parameter Methods

Ze Yang

1, a, *

, Baoqing Yang

1, b

and Jie Ma

1, c

Harbin Institute of Technology, School of Aerospace, Control and Simulation Center, China

Keywords: ADRC, model information, Bessel filter, total disturbance, linear extended state observer (LESO).

Abstract: In the LADRC controller, the former proposes a parameter adjustment method based on bandwidth design,

but the effect still has room for improvement. This article will improve the effects of the controller in two

ways. First, the known model information of the controlled object is introduced into the controller design to

reduce the observer's interference observation load. On the other hand, the filtering methods of Bessel,

Butterworth and Chebyshev are used to design the equivalent design of the extended state observer

parameters, thereby increasing the overall performance of the controller by approximately 60%.

1 INTRODUCTION

The ADRC controller consisting of tracking

differentiator (TD), extended state observer (ESO)

and nonlinear state error feedback control law

(NLSEF) (Jingqing Han, 2009). Among them, ESO

is the core of the controller.

ESO is based on the state observer concept,

which expands various known disturbances or

unknown disturbances that can affect the output of

the system into new state variables that are easily

observed. In theory, there is no need to rely on the

exact mathematical model of the controlled object.

Any second-order victim system and its LESO

can be described as (Jingqing Han, 2007) the

Equation (1):

Among them,

are internal states,

output for the system.

(, )

is acceleration

acting on the open loop system. And think of the

(, )

as an extended state, recorded as

(Jingqing Han, 2007). And record



()t



.According to the existing theory, the above formula

is designed as a linear extended state observer.

Through the observer of the above structure, the

controlled object is compensated as

() /Gs b s

The parameters

123

,,zzz

in (3) is the observation of

the system state

123

is the error signal of the

observed value

is the controller gain, the

selection of this parameter is determined by the

equivalent series integration form of the controlled

object (QIN Chang-mao, QI Nai-ming, ZHU Kai,

2010). If the three parameters

01 02 03





are

selected reasonably, LESO can accurately observe

the system state variables.

The parameter adjustment method of ESO is not

perfect, and it is difficult to implement under

nonlinear conditions, including neural network

algorithm (YIN Jin-song, WANG Rong-line, GAO

Qiang, ZHANG wei, 2019), particle swarm

optimization algorithm (Wang Boyu, 2018) and so

on.In the traditional LESO parameter tuning, there is

a more widely used method called pole placement

method (GAO Zhiqiang, 2003). Through laplace

transform on (2), and after constant transformation

the following results can be obtained.

122 120 111120112302103031

,(,),, , (), (), ()

xx fxx buy xe z yz z yzz z yz buz yz





  



 

(1)

222

0010030

12 3

32 32 32

01 02 03 01 02 03 01 02 03

() () ()

ssy bu ssy bu sy bu

zy zsys z

sss sss sss





    



    

  

(2)

Yang, Z., Yang, B. and Ma, J.

Improved ADRC Controller based on Model Information and Special Filter Parameter Methods.

DOI: 10.5220/0008387603170322

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 317-322

ISBN: 978-989-758-412-1

317

NLSEF

ESO

G(s)

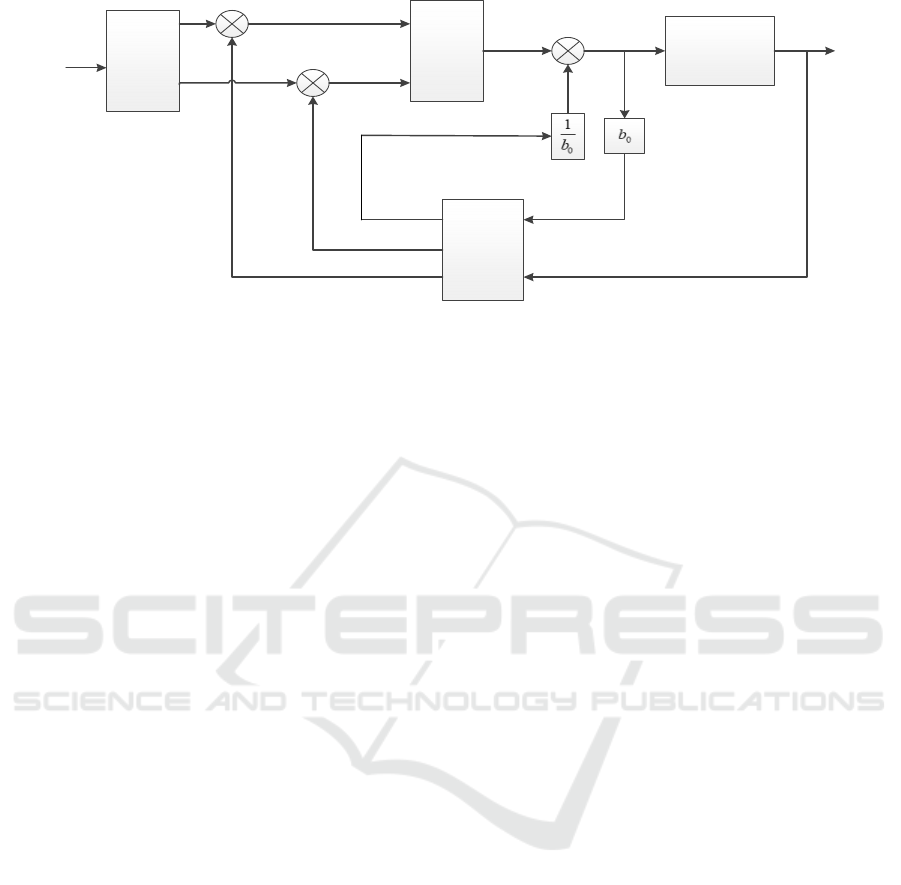
Figure 1. Second-order ADRC controller structure.

303 010203

() / /( )Gs z f s s s





 

(3)

In the Equation (2),

sy bu

is the total

disturbance. So we can get the transfer function

()Gs

from

Through the transfer function relationship

between

and

, we can design the ESO's

observation performance of the total disturbance to

be equivalent to a low-pass filter of the form. The

traditional pole placement method or bandwidth

method is to arrange the poles of the characteristic

equations in the same position. The classic method is

as follows,

01 02 03

3, 3,

qqq



  



(GAO

Zhiqiang, 2003). In the equation,



is the

bandwidth configuration requirement of the

observer.

2 LESO BASED ON MODEL

INFORMATION AND FILTER

METHOD

The content of this section is mainly based on the

previous text. Because the traditional ESO does not

need to rely on the precise information of the

controlled object in theory, it makes it have certain

performance limitations in the process of use. The

combination of ESO and model information can

further reduce the observation burden and improve

the overall performance of the controller (Yao

Xiaoyan, 2018). As mentioned earlier, the

parametric design of the observer can be equivalent

to a specific form of low-pass filter parameter

design, so we can introduce some better filter

methods with better performance than the traditional

pole placement method.

We can design a similar LESO observer equation

through such a system state equation.

Similarly, the system model compensated by the

above observer is changed from

/bs

012

/( )bsasa

Obviously, the system model of the improved

compensation is closer to the ordinary second-order

controlled object in our actual modeling. We can

apply more known parameters to the controller, so

that the total disturbance observation can be

reduced. Reduce the burden on the observer and

avoid the problem of saturation of the system.

The image is a simple second-order controlled

object to perturb the signal, using two ESOs to

compare the results of the total disturbance signal

observation. From the image, we can clearly see that

the improved ESO disturbance observations are

much smaller than the ESO of the traditional

structure, leaving a lot of room for the performance

improvement of the controller.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

318

Figure 2. Comparison of disturbance observations between traditional ESO and improved ESO.

11 1 2 01 12 3 02 1 0 12213 03 1

,(), () ,()ezyzz yzz z yz buazazz yz





          

 

(4)

2.1 Introducing Four Filter Methods to

Improve LESO Parameter Tuning

Method

The Bessel filter is a linear filter with a maximum

flat linear phase response. The transfer function of

the Bessel filter is

() (0)/ ()

nnn

Ts B Bs

,where

()

is Bessel polynomial, which can be obtained

by a recursion formula,

1, 1BBs

, and

can

be written as

(2 1)

nnn

BnBsB



 

According to the pole configuration form we

need, we choose the third-order Bessel low-pass

filter. Its transfer function is in the Equation (5):

Therefore, according to the transfer function

structure parameter comparison, the parameter

formula of LESO can be obtained,





=15





=15





The amplitude-frequency characteristic of the

Chebyshev filter is

(=1/(1+ (/))



）



is the cutoff frequency,



is passband ripple

factor, and n is filter order.

()



is Chebyshev

polynomial, can be written as

cos( cos ( )) n





when





,and

cosh( cosh ( ))n





,when





Chebyshev polynomial is selected as 6 times.

The specific form is

64 2

() 32 -48 18 1T







Take

max



as 1, then bring it into amplitude-

frequency characteristic equation, Solve the filter

transfer function by writing a Matlab program.

So we can get the parameter expression of the

filter in the Equation (6):

Therefore, according to the transfer function

structure parameter comparison, the parameter

formula of LESO can be obtained,

0.98834







1.2384







0.49131







The amplitude-frequency characteristic

expression of the Butterworth filter is



() 1/(1 / )

Qjj





Under ideal conditions, meet the condition

(/ )1





in the passband, and so

(/ )



decreasing gradually and gradually approaching 0 as

N increases. Its amplitude squared function can be

decomposed into 2N poles, and uniformly

symmetrically distributed over the circumference of

radius



. We use a third-order Butterworth filter,

considering the stability requirements of the system,

so we only select the three poles of the left half

plane. They can be written as

111

pq p qpq

ses se









So after a simple transformation and comparison

with (6), the relationship between the observer

parameters and the set bandwidth can be obtained,













03 q







3 SIMULATION VERIFICATION

In this chapter, we model and simulate the above

theory and method to verify the theoretical

feasibility and effect, and combine the turntable

motor to simulate and verify the performance after

applying the new method.

We changed the LESO used in the simulation to

an improved LESO which based on model

information, and compared several of the above

parameter adjustment methods to verify the

performance of the observer under different filter

design methods.

Improved ADRC Controller based on Model Information and Special Filter Parameter Methods

319

32 33 2 2 3

() 15/( 6 15 15) () (15 )/( 6 15 15 )

qqqq

Hs s s s Qs s s s





 

(5)

33 2 2 3

( ) 0.49131 / ( 0.98834 1.2384 0.49131 )

qqqq

Qs s s s



 



(6)

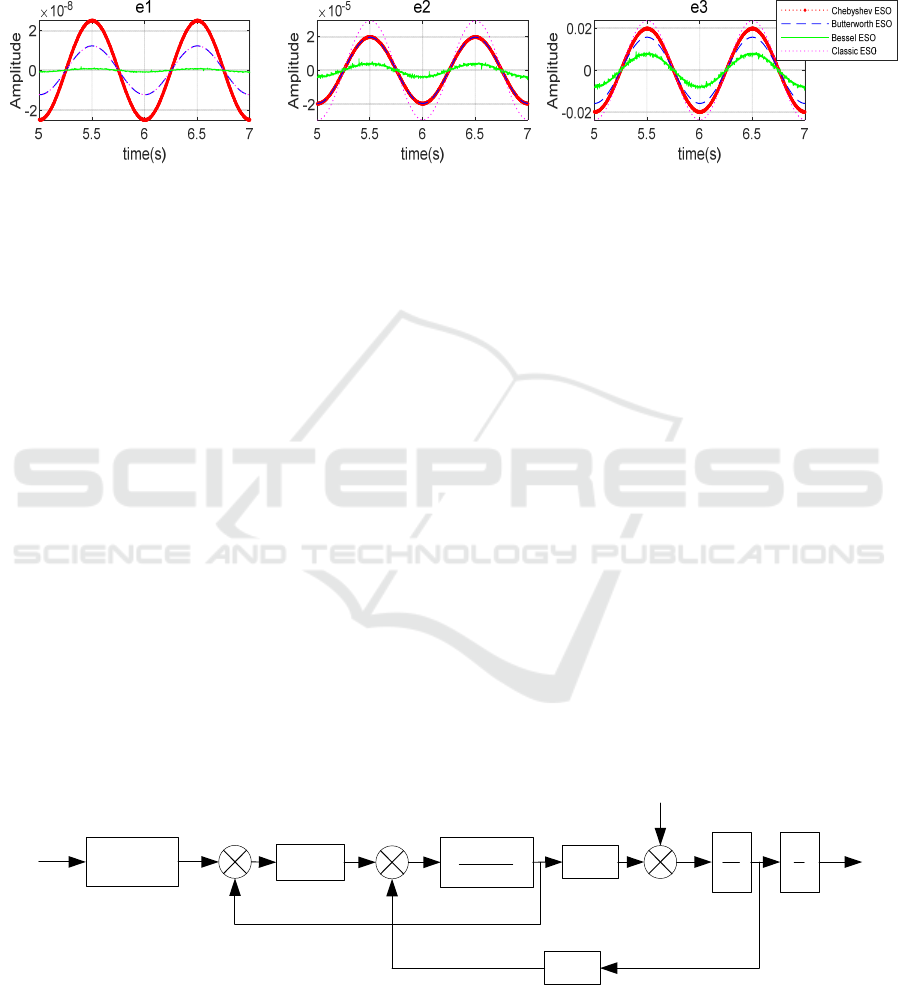
Figure 3. Comparison of classical bandwidth and Chebyshev filter ESO observation error.

Among the above simulation images, since these

parameters tuning methods all depend on the given

bandwidth parameters, we set it as 800 to facilitate

the performance comparison of the observer.

123

,,eee

are the observation errors of

and

respectively.

The observation value of

is the error signal of the

total disturbance, which is an important indicator for

measuring the performance of the observer. It can be

seen that under the method of using the Chebyshev

filter, the observation error value of the total

disturbance signal has reduced compared with the

conventional bandwidth method. And these four

LESO parameters are set in same bandwidth

condition compared with each other. The decrease of

the observation error value, which can help to

improve system performance, and which result will

be verified in subsequent simulations. We can see

from the observation error signal curve that the

LESO with Bessel filter equivalent parameter design

has the highest observation accuracy, and its error

value reduced by about 50%, compared with the

classical bandwidth method and other filter

equivalent parameter design methods.

At present, most of the turntable devices use

permanent magnet synchronous motors as the

actuator. Therefore, in order to verify the application

effect of the above theory, we use permanent magnet

synchronous motor as the controlled object. Its

system block diagram is shown in Fig 4.

We take



as 0.00391909482,



as 0.98095377,

as 89.55074799.

In the simulation verification test, the parameters

of the previous turntable are selected as the basic

conditions, and the system is subjected to

disturbance signals and dead zone characteristics.

Dead zone characteristics are -10 N•m to +10 N•m.

Rate perturbation and position perturbation are 50%

of the input signal amplitude and frequency is

1rad/s.

We use the most common types of signals as

inputs to simulate and verify the performance of the

controller, including sinusoidal signals, step signals,

and ramp signals.

Ls R











Figure 4. Turntable motor equivalent transfer function block diagram.

The equivalent transfer function can be written as:

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

320

() ()/ () (1/ )( / )/( / ( ) / 1)

vps e Te ps Te

G s s R s s k k k LJs k k k r Js k k



 

(7)

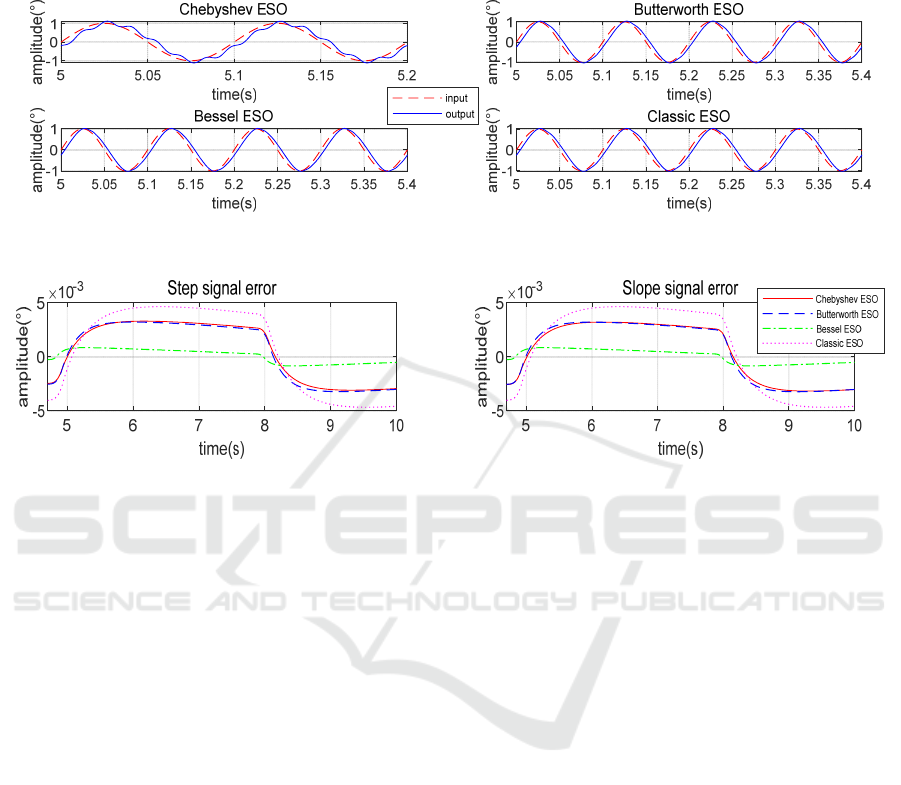
Figure 5. Comparison of 10Hz sinusoidal signal output under four methods.

Figure 6. Comparison of output error under four methods.

We used a 10Hz sinusoidal signal as input to test

the dynamic tracking performance of the system

using different design methods. The standard phase

error should not exceed 10ms, and the amplitude

error should not exceed 10% of the input signal.

Then, we can see the difference between the input

and output amplitudes under the method of using the

Chebyshev filter , its amplitude error is 0.138°, and

its anti-disturbance capability is very bad, and the

output signal has experienced drastic fluctuations,

which cannot meet the indicator requirements. And

the difference between the input and output

amplitudes under the method of using the

Butterworth filter is 0.035° and the phase difference

is 3.491 ms. the difference between the input and

output amplitudes under the method of using the

Bessel filter is 0.033° and the phase difference is

2.405 ms.

Combined with the above results, we can get the

conclusion, the Chebyshev filter method cannot

make the system track the 10Hz sinusoidal signal,

the Bessel filter method is the best, the Butterworth

filter method is second, and the classical bandwidth

method is third.

In the above step response test, we added a

disturbance factor that can simulate the actual

situation of the turntable motor system, such as the

dead zone characteristics in the motor and the low

frequency disturbance at the position output and

speed output. Dead zone characteristics are -10 N•m

to +10 N•m. Rate perturbation and position

perturbation are 50% of the input signal amplitude

and frequency is 1rad/s. It can be clearly seen that

when the Bessel filter method is used, the steady-

state error of the system is the smallest, the

Butterworth filter method is second, the Chebyshev

filter method is third, and the classic bandwidth

method is the largestIf the accuracy of the system is

high, we should use the Bessel filter method for

LESO design. Similarly, we use the ramp signal as

an input to test the system's minimum angular

velocity and detect if the error meets the accuracy

requirements. The ramp signal slope is 0.002°/s.

From the results, the best is still Bessel method, the

second is the Chebyshev, Butterworth. The classic

bandwidth method has the largest steady-state error.

4 CONCLUSION

We propose the Bessel filter method, the

Butterworth filter method, and the Chebyshev filter

method. In the simulation results, we can find that

among the above three design methods, the Bessel

Improved ADRC Controller based on Model Information and Special Filter Parameter Methods

321

filter method shows good controller performance

under various input signals. Among them, the Bessel

filter design method has the best performance. In the

future, in the design of the servo system controller,

we can use the information of the controlled object

model and several filter equivalent parameter design

methods proposed in this paper to meet the

increasing precision requirements. In the servo

control system, if there is a high demand for

accuracy and anti-disturbance capability, the

parameter design method mentioned in this paper

can be applied.

REFERENCES

GAO Zhiqiang. Scaling and bandwidth-parameterization

controller-tuning [C] //Proceedings of the 2003

American Conference. Denver: IEEE, 2003, 6: 4989-

4996.

Guozhang, Gao,Shipeng Zhang,Lan Gao. Research on

excitation control system of marine brushless

generator base on ADRC [J]. SHIP SCIENCE AND

TECHNOLOGY, 2018, 40(21):116-120.

Jingqing Han. Active Disturbance Rejection Control

Technology - Control Technique for Estimating

Compensation Uncertain Factors [M]. National

Defense Industry Press. 2009.

Jingqing Han. Active Disturbance Rejection Control

Technology [J]. Frontier Science, 2007(01):24-31.

QIN Chang-mao, QI Nai-ming, ZHU Kai. Active

disturbance rejection attitude control design for

hypersonic vehicle [J]. Systems Engineering and

Electronics, 2010, 33 (7): 1607-1610.

Wang Boyu. Intelligent Algorithm - Based Optimization

Design and Application of Active Disturbance

Rejection Controller [D]. Northeast Petroleum

University, 2018.

Yao Xiaoyan. Research on design method of active

disturbance rejection controller for electric load

simulator [D]. Harbin Institute of Technology, 2018.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

322