Application of ARMA Model in Prediction of Development Trend of

Partial Discharge

Hui Xia

1, a

, Chenhao Zhao

2, b

, Zhiguo Tang

2, c

, Deguan Wu

1, d

, Hongyuan Li

1, e

, Kai Pan

1, f

Test & Maintenance Center of CSG EHV Transmission Company, Kunming, China

State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power

University, Beijing, China

345845596@qq.com

Keywords: Partial discharge, ARMA model, trend, prediction.

Abstract: Nowadays, gas insulated switchgear (GIS) has been widely used in power systems. Due to some external

factors, there may be defects in GIS, and some minor defects are difficult to find in the early stage. However,

partial discharges (PD) is easy to occur in the defects and make the defect large, which may cause the

failure of GIS and bring about huge economic losses to both power systems and society eventually.

Therefore, it is helpful to discover the defect discharge in time and predict its development trend for the

early warning of fault and taking suitable countermeasures. In this paper, ARMA model is selected to

predict the development trend of partial discharge, and partial discharge experiment and three kinds of

defect models are designed evaluate the prediction effect of the ARMA model. Finally, the conclusion is

drawn that ARMA model can accurately predict the development trend of linear characteristic parameters,

but it cannot predict that of irregular characteristic parameters of PD accurately.

1 INTRODUCTION

Since the 1970s, gas insulated switchgear (GIS) has

been widely used in power systems due to its high

reliability and compact structure (Кучинский, 1984;

Qiu, 1994; Bolin, 2005). Due to some mistakes in

the process of production, transportation, assembly,

etc., there may be typical defects which will lead to

partial discharge (PD) such as the suspension

discharge, corona discharge and the discharge of

void inside the insulating material(Qi, Li, Hao, 2011;

Liu, Wang, LI, 2013). Under long-term working

conditions, partial discharge will cause insulation

degradation, which will easily lead to GIS failure

during operation, and affect the stable operation of

the power system (Martin, Li, Tsutsumi, 2012;

Pharmatrisanti, Meijer, Smit, 2004). In recent years,

many GIS faults caused by PD at the position of

insulation defects have been discovered, which has

caused great losses to the power system (Ren, Dong,

Qiu, 2017; Tang, Tang, Li, 2017; Zhou, Tang, Tang,

2006). Therefore, it is necessary to study the

development of partial discharge generated by

defects in GIS, and predict the development trend of

PD, which helps to warn the occurrence of faults and

avoid serious losses(Strachan, McArthur, Judd, 2005;

Li, Sun, Du 2002; Liu, Lv ,Li,2004; Qi, Li, Xing,

2014).

H. Okubo et al. used a breakdown prediction

parameter which characterizes the change of PD to

predict the time to breakdown (Okubo, Kato,

Hayakawa, 1998). However, the mechanism of

partial discharge are complicated and the

phenomenon is always affected by various factors

such as operating voltage and load of equipment,

which makes the development of partial discharge

nonlinearly and randomly. So, it is not rigorous to

characterize the development of partial discharge

with one or several parameters. Many studies around

the world have shown that long-term predictions of

the development trend of partial discharges are very

difficult. But, the partial discharge in a short time is

relatively stable. Therefore, we can extract linear

characteristic quantities from the characteristic

fingerprint of PD, and use those linear quantities to

predict the development trend of discharge for a

short time. Short-term prediction can obtain the

discharge development trend within a few minutes

or hours before the failure occurs and realize the

390

Xia, H., Zhao, C., Tang, Z., Wu, D. and Pan, K.

Application of ARMA Model in Prediction of Development Trend of Partial Discharge.

DOI: 10.5220/0008856103900397

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 390-397

ISBN: 978-989-758-412-1

failure warning, which is also very meaningful in

engineering.

In this paper, the aging experiment platform of

GIS PD defect model is built. Three typical GIS

defect models are designed for accelerated aging test

and the UHF detection technology is used to collect

the PD signal. Finally, the ARMA prediction model

is introduced to predict the development trend of

partial discharge in a short-term.

2 EXPERIMENTAL SETUT

2.1 Test Circuit Setup and Test Model

Figure1 shows the 220 kV GIS partial discharge test

platform. TC1 and TC2 are two test chambers for

setting the discharge defect model. S1 and S3 are

internal UHF sensors, and S2 and S4 are external

UHF sensors that receives PD signals radiated by a

defect discharge inside the cavity through a pouring

hole at the disc insulator. The partial discharge

signal coupled by the sensor is processed by the

signal conditioner, then, one channel is connected to

the oscilloscope, and the other is uploaded to the

computer via the embedded data processing unit.

The oscilloscope is Agilent MSO9404A with a

sampling rate of 20 GSa/s and a bandwidth of 4 GHz.

In this experiment, three defect models are

designed, which are the suspension defect on the

high voltage side, surface discharge defect and

suspension defect on the ground side. The model of

suspension defect on the high voltage side is formed

by placing a shield on the high voltage conductor of

GIS and making the shield contact with the

conductor incompletely. The model of suspension

defect on the ground side is formed by placing the

M10 bolt at the interface between the disc insulator

and the shell of GIS. The surface discharge model is

formed by sticking a 3 cm metal wire on the surface

of disc insulator with sticky tape. Three defect

models are shown in Figure 2, Figure 3 and Figure 4,

respectively. The last step is to place the defect

models in the test chamber filled with SF6 gas with

a pressure of 0.5 MPa.

Signal Conditioning and Embedded

Processing Unit

Oscilloscope

AC220V

T1 T2

TC1

TC2

Figure 1. The schematic of test.

Figure 2 .Suspension defect on the high voltage side in

GIS.

Figure 3. Suspension defect on the ground side in GIS.

Figure 4. Insulation surface discharge defect in GIS.

Applied Votage

/kV

Test Time/min

Figure 5.The test voltage curve of suspension defect on the

high voltage side

Application of ARMA Model in Prediction of Development Trend of Partial Discharge

391

Applied Votage

/kV

Test Time/min

Figure 6. The test voltage curve of suspension defect on

the ground side.

Test Time/min

Applied Votage

/kV

Figure 7. The test voltage curve of surface discharge

defect.

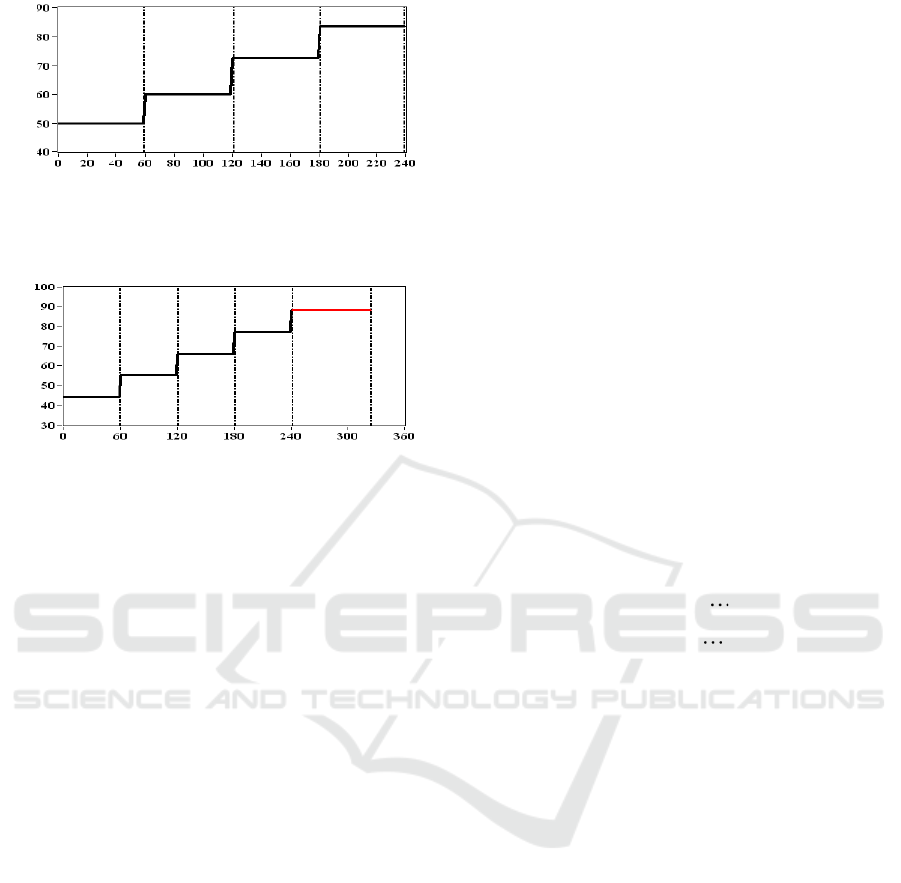
2.2 Experimental Process

Firstly, the voltage applied to the high voltage side

of the GIS is slowly increased until stable PD signals

appear, and then the voltage is increased step-by-

step to accelerate the degradation of the defect.

Taking the test of suspension defect on the high

voltage side as an example, when the applied voltage

reaches73.5kV, relatively stable PD signals appeared.

Then the voltage was increased step by step and

maintained 1 hour at 73.5, 77, 80.5, 84, 87.5, 91,

94.5, 98kV respectively. Then, in order to further

accelerate the degradation of the defect, the voltage

was raised to 102 kV, and then the test was stopped

after keeping the voltage at 95 kV for 2 hours. The

curve of applied voltage of floating defect is shown

in Figure 5, and the curve of applied voltage of

surface discharge defect and insulator-metal

discharge defect are shown in Figure 6 and Figure7

respectively.

It should be specially noted that in the final stage

of the test of surface discharge, the voltage was risen

to 85 kV, and flashover occurred after 1 hour and 25

minutes.

3 THE PREDICTION PRINCIPLE

OF ARAM MODEL

3.1 ARMA Model

Auto-regressive and moving average (ARMA)

Model is a kind of stochastic time series model,

which is widely used in various fields (Yang, Chen,

Shen, 2018; Kang, Qi, Liu, 2012). It usually uses the

random characteristics of time series to describe the

evolution of a phenomenon, that is, it uses the past

and current values of time series and the weight of

the random disturbance factor to model and predict

the evolution of time series. ARMA is an important

method to study time series.

Auto-regressive (AR) model and moving average

(MA) model are important time series model. The

AR model predicts future values by a linear

combination of past observations and current

interference values, and the MA predicts future

values by a linear combination of past interference

values and current interference values. ARMA

model is a combination of AR model and MA model,

and its mathematical formula is

(1)

In this formula, yt is time series; Φi and θi (i=

1,2 3…….p) is indefinite coefficient, p and q are

order of the model; εt is the deviation due to

interference.

Some time series are sets of time-dependent

variables. Although there is uncertainty in the single

value of the time series, the whole sequence changes

regularly which can be described by relevant

mathematical models. That is the basic idea of using

ARMA model to predict the development trend of

partial discharge. Mathematical models help to

understand the structure and characteristics of time

series fundamentally, and contribute to obtain the

optimal prediction in the sense of minimum variance.

Therefore, it is very suitable to analyze short-term

process of PD by means of math models and predict

the development trend.

3.2 Procedures of Modeling

Procedures of modeling is shown in Figure 8 and

detailed steps are as follows.

1 1 2 2

t t t p t p

t t t q t q

y y y y

  

      

  

    

   

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

392

(1) Calculate the values of the sample auto

correlation function (ACF) and the sample partial

auto correlation function (PACF).

The formula of ACF is

(2)

And the formula of PACF is

(3)

There are two matrix in the formula of PACF,

those are

ˆ ˆ









(4)

And

(5)

(2) Selected and fitting the ARMA (p, q) model

with appropriate order according to the characters of

the ACF and PACF.

(3) Estimate the values of indefinite coefficient

in the model.

After fitting the model, the next step is to

estimate the unknown coefficient in the model.

(4) Verify the validity of the model.

A valid model means that the model contains

almost all the information of the data, so that the

residual does not contain any relevant information,

this is, residual is white noise series. Therefore,

white noise test need to be performed for the

residual of fitted model. If the results of the test

show that the residual is not white noise, the model

is considered to be not valid.in this case, other

models need to be considered.

If the fitted model passes the white noise test,

then steps (2)-(4) continue to be performed to

establish multiple fitted models with full

consideration of various possibilities. and selecting

the optimal model from all the fitted models that

pass the test.

(5) Optimizing the model.

The optimal model is selected from all the fitted

models that pass the test. Akaike information

criterion (AIC) is a standard used to weigh the

goodness of fit, and evaluate the complexity of the

model and the ability of the model to fit the data.

The more parameters of the model, the wider the

range of models that can be selected and the more

accurate the model is. However, with the increase of

parameters, the parameter estimation is more and

more difficult, and the accuracy of estimation is

getting lower. Therefore, a good model should reach

a certain balance between the accuracy of the model

and the accuracy of parameter estimation.

Usually, AIC is defined as AIC= -2log

(maximum likelihood value of the model) + 2

(number of unknown parameters of the model). The

model with the smallest AIC value is the optimal

model.

(6) Use the fitted model to predict the future

trend of the series.

4 SHORT-TERM PREDICTION

OF PARTIAL DISCHARGE

4.1 Short-term Prediction for Linear

Characteristic Parameters of PD

By processing the test data of the suspension

discharge on the high voltage side, the variation

curve of the discharge phase width is shown in

Figure 9. The discharge phase width varies linearly

with the test time, so its data is selected to evaluate

the accuracy of the development trend of linear

characteristic parameters of PD predicted by the

ARMA prediction model. The total test time is 600

minutes and the data of the first 200 minutes is used

to model and predict the development trend of

partial discharge phase width in different time

periods.

( )( )

()

t t k

x x x x





















ˆ ˆ

ˆ ˆ ˆ

k k k



  





Application of ARMA Model in Prediction of Development Trend of Partial Discharge

393

Translate into

stable series

Abandon the

time series

START

STOP

Time series

is stable

Pass white

noise test

Verify model

validity

Calculate ACF and PACF

Fitting ARMA model

Estimate unknown coefficient

Optimizing the model

predict future tendency

Figure 8. ARMA modeling process.

As can be seen from Figure 10, the predicted

values differ little from the true values with different

prediction times. It can be seen from the relationship

between the prediction time and the prediction error

shown in Figure 11. In the range of the prediction

time of 0-400, the prediction error is kept within

10%, which indicates that for the linearly varying

partial discharge characteristic parameter, it is

feasible to predict short-term trend by ARMA model.

Test Time/min

Figure 9. The change trend of phase width of suspension

discharge on the high voltage side.

Test Time/min

(a) The curve of 50 minutes prediction

Test Time/min

(b) The curve of 200 minutes prediction

Test Time/min

(d)The curve of 400 minutes prediction

Figure 10. Predicted curves in different prediction time.

Prediction Time/min

Prediction Error

Figure 11. Predicted error with different prediction time.

4.2 Short-term Prediction for Step

Characteristic Parameters of PD

By processing the test data of the suspension

discharge on the ground side, the variation curve of

the discharge interval number is shown in

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

394

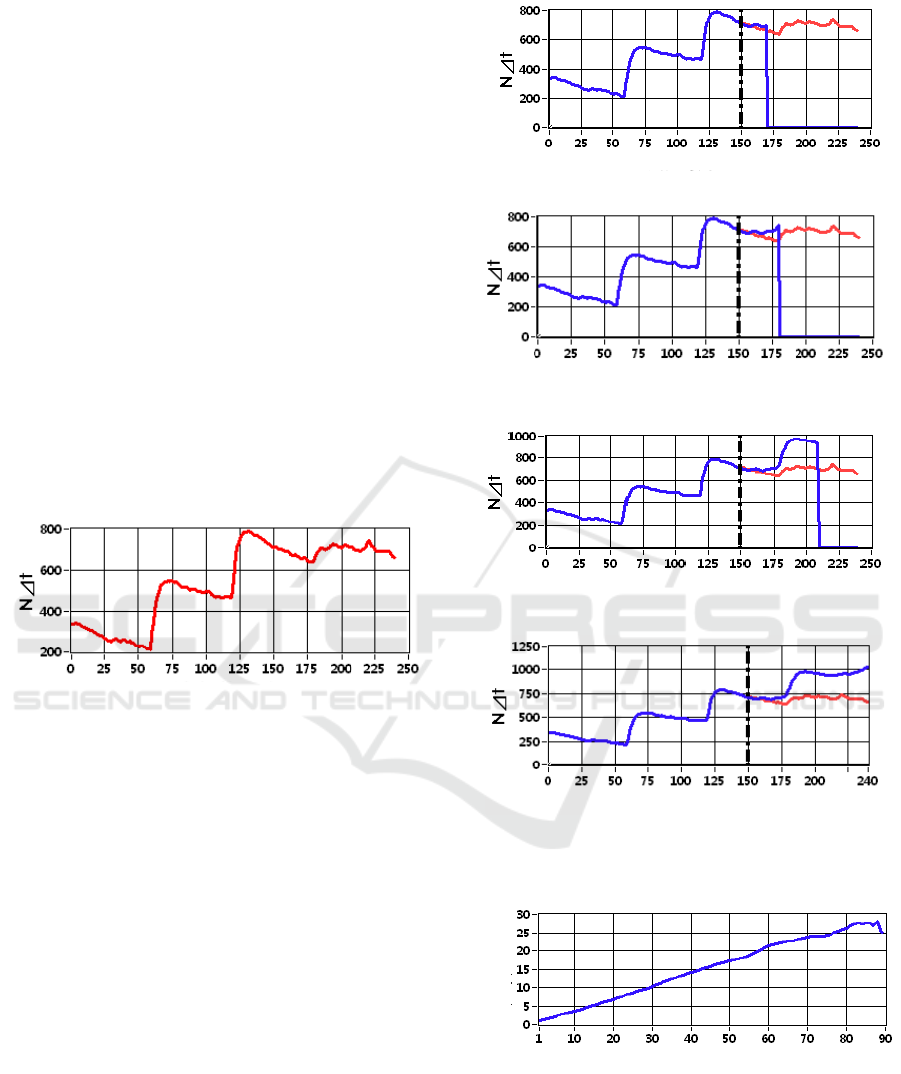
Figure12.The discharge interval number of the

insulator-metal discharge step increase with the test

time, so its data is selected to evaluate the accuracy

of the development trend of step characteristic

parameters of PD predicted by the ARMA prediction

model. The total test time is 240 minutes and the

data of the first 150 minutes is used to model and

predict the development trend of discharge interval

number in different time periods.

It can be seen in the Figure 13 that as the

prediction time increases, the difference between the

predicted value and the true value gradually widens.

As shown in Figure 14, when the prediction time is

less than 30 minutes, the prediction error can be kept

within 10%, and then the error increases with the

extension of the prediction time. The reason of

increase of subsequent prediction error is that the

third step of the true value changes less than the first

two. In general, the ARMA model cannot accurately

determine the size of the step, but it can predict the

development trend of step characteristic parameters

of partial discharge roughly.

Test Time/min

Figure 12. The change trend of discharge interval number

of suspension discharge on the ground side.

4.3 Short-term Prediction for Irregular

Characteristic Parameters of PD

By processing the test data of the insulation surface

discharge, the variation curve of the information

entropy of discharge amplitude is shown in Figure

15. The information entropy of insulation surface

discharge amplitude increase with the test time

irregularly, so its data is selected to evaluate the

accuracy of the development trend of irregular

characteristic parameters of PD predicted by the

ARMA model. The total test time of insulation

surface discharge is 386 minutes and the data of the

first 250 minutes is used to model and predict the

development trend of discharge interval number in

different time periods.

Test Time/min

(a) The curve of 20 minutes prediction

Test Time/min

(b) The curve of 30 minutes prediction

Test Time/min

(d) The curve of 90 minutes prediction

Figure 13. Predicted curves in different prediction time.

Prediction Time/min

Prediction Error

Figure 14. Predicted error in different prediction time.

It can be seen from Figure 16 and Figure 17 that

as the prediction time increases, the difference

between the predicted value and the true value

increases rapidly, and the prediction error is greater

than 10%, which indicates that it is difficult for the

Application of ARMA Model in Prediction of Development Trend of Partial Discharge

395

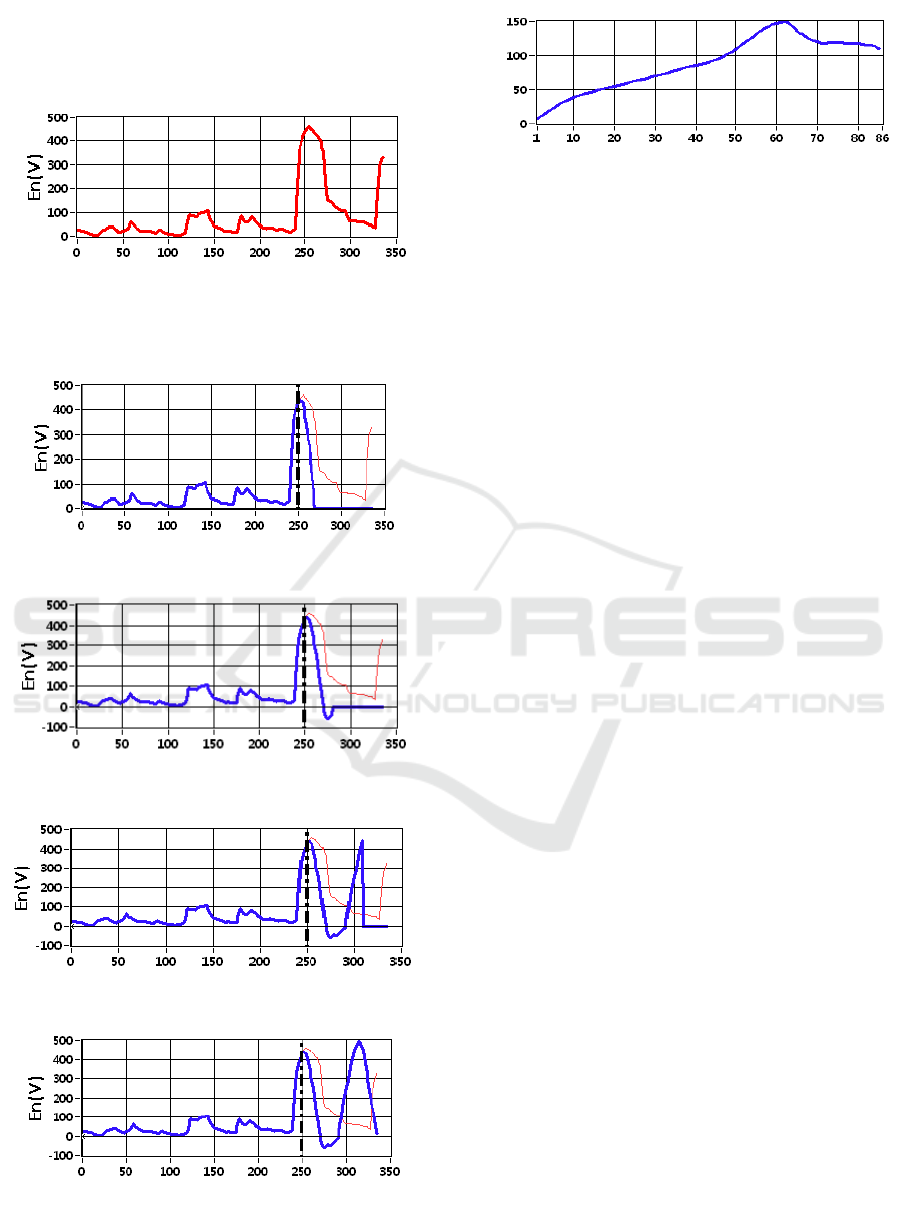
ARMA model to accurately predict the trend of

irregular characteristic parameters. However, the

ARMA model can predict the approximate trend, as

shown in Figure 16.

Test Time/min

Figure 15. The change trend of entropy of insulator

surface discharge amplitude width with test time.

Test Time/min

(a) The curve of 20 minutes prediction

Test Time/min

(b) The curve of 30 minutes prediction

Test Time/min

(d) The curve of 86 minutes prediction

Figure 16. Predicted curves in different prediction time.

Prediction Time/min

Prediction Error

Figure 17. Predicted error in different prediction time.

5 CONCLUSION

In order to obtain the partial discharge data of

typical defects, a partial discharge test platform

containing three kinds of defects and was built in

this paper, and experiments were carried out.

Aiming at the early warning of fault caused by

partial discharge defect, the ARMA model

prediction theory and the process of modeling are

introduced in detail. Based on the obtained partial

discharge data, the ARMA model was used to

predict the development trend of partial discharge,

and the prediction results were analysed. Finally, the

following conclusions were obtained.

(1) The effect of short-term prediction of ARMA

model is different for the characteristic parameters

with different development trends. For linear

characteristic parameters of partial discharge, the

ARMA model can accurately predict the short-term

trend of the characteristic parameters, and the

prediction error is smaller; for the partial discharge

characteristic parameters with step change, when the

prediction time is less than 30 minutes, the

prediction error is less than 10%. But the prediction

error will increase with the extension of the

prediction time. For the irregular characteristic

parameters of partial discharge, the prediction effect

of ARMA model is not good. The ARMA model can

roughly predict short-term trend of irregular

characteristic parameters, but it is difficult to make

accurate prediction.

(2) In the substation, the on-line detection system

can collect the partial discharge signal in real time

and analyse the variation trend of the typical

characteristic parameters. Based on these parameters,

appropriate prediction model can be selected to

predict the development trend of the partial

discharge, which is of great significance for fault

warning and stable operation of electrical equipment.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

396

ACKNOWLEDGEMENTS

This research was supported by the Science and

Technology Projects of Test & Maintenance Center

of CSG EHV Transmission Company (Grant No.

CGYKJXM20160025).

REFERENCES

Bolin, P., and Koch, H.. 2005. Introduction and

applications of gas insulated substation (GIS), IEEE

Power Engineering Society General Meeting.

Кучинский, Г. С., 1984. Partial discharge of high voltage

electrical equipment, China Water Conservancy and

Electric Power Press.

Kang, H. , Qi, Y. , Liu, G., et al., 2012. Application of the

ARMA Model in Non-stationary Vibration Signals.

International Conference on Quality, IEEE..

Li. J., Sun, C.X., Du, L., et al., 2002. Study on Fractal

Dimension of PD Gray Intensity Image. Proceedings

of the CSEE, 22, p. 123-127,.

Liu, Y.P., Lv, F.C., and Li, C.R., 2004. Study on pattern

spectrum of patial. Proceedings of the CSEE, 24,

p.179-183.

Liu, Y. P., Wang, Z. J., Li, Y. S., 2013. Study on the

Insulating Spacers Surface Discharge of GIS. Applied

Mechanics and Materials, 385-386, p. 1209-1212.

Martin, Y., Li, Z., Tsutsumi, T., et al.,2012. Detection of

SF6 Decomposition Products Generated by DC

Corona Discharge Using a Carbon Nanotube Gas

Sensor. IEEE Transactions on Dielectrics and

Electrical Insulation, 19, p. 671-676.

Okubo, H., Kato, T., Hayakawa, N., et al., 1998. Temporal

Development of Partial Discharge and Its Application

to Breakdown Prediction in SF/sub 6/ gas. IEEE

Transactions on Power Delivery, 13, p. 440-445.

Pharmatrisanti, A., Meijer, S., and Smit, J. J., 2004.

Probability of Partial Discharge Detection in Aged

GIS due to Void in Epoxy. Gaseous Dielectrics X.

Springer US.

Qiu, Y.C., 1994. GIS device and its insulation technology,

China Water Resources and Electric Power Press.

Qi, B., Li, C.R., Hao, Z., et al., 2011. Evolution

phenomena and features of surface partial discharge

initiated by immobilized metal particles on GIS

insulators, Proceedings of the CSEE, 31(1), p. 101-108.

Qi, B., Li, C.R., Xing, Z.L., et al., 2014. Partial Discharge

Initiated by Free Moving Metallic Particles on GIS

Insulator Surface: Severity Diagnosis and Assessment.

IEEE Transactions on Dielectrics and Electrical

Insulation, 21, p. 766-774.

Ren, M., Dong, M., and Qiu A.C., 2014. Partial

Discharges in SF6 Gas Filled Void under Standard

Aperiodic and Oscillating Switching Impulses. IEEE

Transactions on Dielectrics and Electrical Insulation,

21, p. 262-272.

Strachan, S.M., McArthur, S.D.J., Judd, M.D., et al, 2005.

Incremental Knowledge-based Partial Discharge

Diagnosis in Oil-filled Power Transformers.

Intelligent Systems Application to Power Systems, 130,

p.181-186.

Tang, Z.G., Tang, M.Z., Li, J.Z., et al, 2017. Review on

Partial Discharge Pattern Recognition of Electrical

Equipment. High Voltage Engineering, 7, p.173-187.

Yang, Q., Chen, S.Z., Shen, S.M., et al., 2018.

Adaptability of LSTM Network and ARMA Modeling

to Random Error Prediction of Inertial Devices.

Electronics Optics & Control, 25, p. 68-72.

Zhou, Q., Tang, J., Tang, M., et al, 2006. Mathematical

Model of Four Typical Defects for UHF Partial

Discharge in GIS. Proceedings of the CSEE, 26, p. 99-

105.

Application of ARMA Model in Prediction of Development Trend of Partial Discharge

397