Establishment and Simulation of the Damping Torque Model of

Hydraulic Intelligent Knee Prosthesis

Jinyue Sun

1, 2, a

, Qiaoling Meng

1, 2, b

, He Lan

1, 2

, Zongqi Jiao

1, 2

and Hongliu Yu

1, 2

Institute of Rehabilitation Engineering and Technology, University of Shanghai for Science and Technology, Shanghai

200093, P.R.China

Shanghai Engineering Research Center of Assistive Devices, Shanghai 200093, P.R.China

Keywords: Hydraulic, intelligent knee prosthesis, damping torque, dynamics model, simulation.

Abstract: The intelligent knee prosthesis structure was designed and the dynamics model of the lower limb prosthesis

system and hydraulic damper model were established in this paper. The flow area which adjusted the

damping torque was identified through the combination of hydraulic damper model and dynamics model.

The comparable analysis was done based on the Matlab simulation of damping torque curve with theoretical

curve. The damper opening of the specific speed was determined. The trend of the knee joint moment curve

produced by the hydraulic damper is consistent with the theoretical moment curve under different flow areas.

The damping moment of hydraulic knee joint can be controlled by adjusting the flow area. The proposed

damping torque model can provide effective guidance for the determination of the flow area and have

important consequences for adjustment of damping torque. Providing theoretical model of the damping

torque control for the hydraulic intelligent knee prosthesis.

1 INTRODUCTION

Human gait can be divided into two periodic

repeating phases: stance phase and swing phase. The

function of the above-knee prosthesis is to maintain

the stability of the knee in the stance phase and

provide essential damping in the swing phase (Kun

Shang, et al., 2009). Therefore, prosthetic knee joint

is the most important and complex component of the

above-knee prosthesis. Knee torque limits whether

the maximum knee flexion is close to the

physiological gait. And it determines whether the

shank can decelerate smoothly until knee fully

extend and the magnitude of the ground impact

when the heel strikes the ground. Inappropriate knee

torque control will lead to abnormal gait, reduce gait

symmetry, and increase energy consumption of the

wearer (Chunxia Zhao et al., 2015). The control of

knee joint moment can be divided into three kinds:

constant friction, mechanical spring and damper

control. The control mechanism is that the moment

curve generated at the knee joint is close to the

moment curve under the physiological gait, so that

the shank swing is close to the physiological gait

(Yanli Geng et al., 2013). According to whether the

knee joint can produce active moment, the knee

prosthesis can be divided into active prosthesis and

passive prosthesis. Passive knee prosthesis uses

pneumatic pressure, hydraulic pressure,

magnetorheological and other dampers to generate

damping torque, while active knee prosthesis

generates active torque through motor, pneumatic

muscle, micro hydraulic pump and so on. Intelligent

knee joint refers to the application of microcomputer

technology and intelligent control technology to the

control of knee joint damper, so that the knee joint

torque can be automatically adjusted with the change

of walking speed and joint angle in order to make

the gait symmetry and tracking more closely to

healthy people (Tengyu Zhang et al., 2016).

The control of knee torque is always the

importance and difficulty of research. Dundass

studied the effect of degradation of the hydraulic

damper on a patient's gait. In order to eliminate the

influence of variables on gait in the gait experiment,

a dynamic model was established based on the gait

data of patients in the experiment. The ground

reaction force predicted by this dynamic model is

consistent with the experimental data. However, the

drawback is that the model is only for one

experimental patient, and it is not universal

(Dundass et al., 2003). Furse improves the control

Sun, J., Meng, Q., Lan, H., Jiao, Z. and Yu, H.

Establishment and Simulation of the Damping Torque Model of Hydraulic Intelligent Knee Prosthesis.

DOI: 10.5220/0008856302030209

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 203-209

ISBN: 978-989-758-412-1

203

performance of swing phase torque by adding two

series springs to the friction brake single-axis

passive knee prosthesis, but it is difficult to apply to

the intelligent knee prosthesis with hydraulic and

pneumatic control (Furse et al., 2011). Based on the

concept of energy flow in human gait, Unal

proposed the passive control mechanism of reducing

energy consumption of swing phase by using three

elastic energy storage elements (Unal et al., 2010).

Dabiri designed a passive hydraulic damping

controller for swing phase of uniaxial knee

prosthesis, but the experimental results show that the

maximum flexion angle controlled by the damper is

quite different from that of normal people, and the

control effect is not ideal (Dabiri et al., 2009).

Tahani and Karimi proposed a dynamic model of

lower limb prosthesis based on torsion spring control,

and optimized the control parameters of swing phase

motion (Tahani et al., 2010). Suzuki optimized the

dynamics of the musculoskeletal model of the stump

to obtain the friction value of the passive knee

prosthesis and minimize the energy consumption of

the swing muscle (Suzuki, 2010). Based on the

control parameters of nonlinear hydraulic damper,

Hongliu Yu proposed a dynamic model of swing

phase for intelligent lower limb prosthesis, and the

dynamic relationship between the opening of

damper needle valve and the velocity of swing phase

is identified. But this research model think the

velocity of damper piston is constant, and it is

different from the actual piston velocity (Hongliu Yu

et al., 2010).

Domestic and foreign researchers have proved

the feasibility of the application of damper in the

torque control of knee prosthesis. However, there are

still relatively few studies on the design of

appropriate intelligent knee prosthesis structure, the

construction of dynamic model of the complete

system composed of knee damper and stump, and

the evaluation of the torque control performance of

intelligent knee prosthesis. This study designs a kind

of intelligent knee prosthesis with hydraulic damper

and establishes the dynamic model of the lower limb

prosthesis system and the coupled hydraulic damper

damping torque model. In this study, the torque

control of the knee prosthesis of the dynamic model

is simulated by Matlab, and the effectiveness of the

damping torque model and the rationality of the

designed intelligent knee prosthesis hydraulic

damper structure are proved.

2 MATERIAL AND METHODS

The function of the knee prosthesis is to maintain

stability in the stance phase and provide proper

damping in the swing phase. At present, the damper

used in intelligent knee prosthesis is mainly

hydraulic control, pneumatic control,

magnetorheological control and hydraulic and

pneumatic hybrid control. Pneumatic damping is

small. So it is difficult to guarantee the stability of

the stance phase and commonly used in multi-axis

knee prosthesis. Magnetorheological fluid damper

changes the magnetic field intensity and the

viscosity of fluid by changing the current, so the

damping force at the knee prosthesis is changed to

control the moment of knee prosthesis. But the

control mechanism of magnetorheological fluid

viscosity changes still need to be researched. In

addition, it cannot be close to places with strong

magnetic and electric fields, which limits the range

of use. Hydraulic damper can provide strong

damping when the volume is small, which can

effectively ensure the stability of the stance phase.

So it is mostly used for uniaxial knee prosthesis

(Wujing Cao et al., 2016).

2.1 Structural Design of Knee

Prosthesis

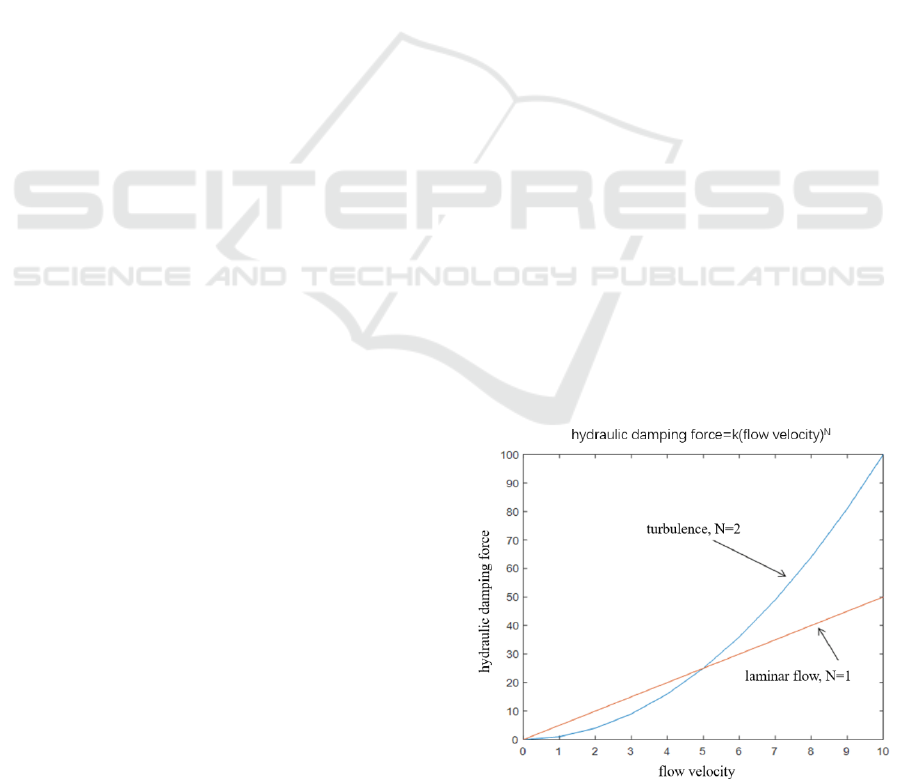
Hydraulic damping force presents different

properties with the change of hydraulic fluid

velocity. When the flow velocity is slow, the

damping and velocity are linear, that is, the damping

is proportional to the flow velocity. When the

velocity is large, the increase of damping is

nonlinear, that is, damping is proportional to the

Figure 1. Relation of flow speed and damping force.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

204

Figure 2. Knee prosthesis structure.

square of velocity (Staros & Murphy, 2013). When

the hydraulic oil flows through the small hole in the

circular tube in laminar flow state, the flow velocity

will increase instantly due to the sudden decrease of

flow area, resulting in turbulence. The relationship

between hydraulic damping force and flow velocity

change is shown in Fig. 1. This property makes it

possible to adjust the damping force of knee joint at

different speeds by changing the flow area of

hydraulic fluid. And then it changes the velocity of

hydraulic oil to create turbulence to achieve rapid

adaptation and control of damping torque. This is

very beneficial to the acquisition of the

physiological gait of the knee swing phase.

Therefore, uniaxial hydraulic knee joint structure is

selected (Hongliu Yu et al., 2009). In order to realize

the independence of intelligent knee flexion and

extension damping torque control, two motors are

used to control the corresponding plug valve

respectively. The flow area of the oil passage is

changed by the DC motor rotating plug valve, so

that the flow rate of the hydraulic oil is

instantaneously increased to form turbulent flow and

cause pressure loss. And then it controls the pressure

difference between the upper and lower chambers to

generate the damping force so as to achieve the

control of the knee damping torque at different

speeds. The overall knee structure is shown in

Figure 2. In order to ensure that the damping of the

flexion oil passage and the extension oil passage do

not affect each other, a check valve is placed in each

of the two oil passages. When the knee is flexed and

the hydraulic piston moves downward, the check

valve in the extension oil passage is closed and the

check valve in the flexion oil passage is opened.

And then the hydraulic oil can only enter the upper

chamber from the lower chamber through the flexion

adjustment oil passage. When the knee is extended

and the hydraulic piston moves upward, the check

valve in the flexion oil passage is closed and the

check valve in the extension oil passage is opened.

And then the hydraulic oil can only enter the lower

chamber from the upper chamber through the

extension adjustment oil passage. In order to assist

the knee extension, a spring is placed in the bottom

of the hydraulic cylinder. In each phase state, the

opening of the hydraulic damper valve is controlled

to adjust the flow rate of the hydraulic oil and then

control the knee damping torque. The magnitude of

the damping torque is proportional to the square of

the knee angular velocity.

=M CV

(1)

M is the knee damping torque, V is the knee

angular velocity obtained by deriving the knee angle

signal, and C is the knee dynamic damping constant.

Five valve opening degrees, namely five different

damping constant values, are controlled during a

given walking cycle to achieve five phase

adaptations and adjustments. The damping value is

adjusted only when the gait phase transforms or the

period changes, and the damping constant is not

adjusted within a certain gait phase. The purpose of

the intelligent knee prosthesis adaptive control

system is to determine the damping constant which

is adapted to the phase state, that is, to control the

appropriate valve opening when the state transforms,

and then the physiological gait is achieved.

2.2 Dynamic Modeling of Lower Limb

Prosthetic System

The uniaxial knee prosthesis is connected to the

wearer's thigh stump through the prosthetic socket.

In order to design the knee controller, the thigh

motion experimental data is provided to the system

dynamics model to obtain the expected knee

damping torque curve. The damping torque curve

actually provided by the hydraulic damper is

obtained by adjusting the flow area of the hydraulic

damper in Matlab. The difference between the

simulation curve and the theoretical curve is

analyzed and compared, and the optimal flow area of

the hydraulic damper at different speeds is obtained.

The dynamic model is validated to provide

theoretical guidance for the control of the knee joint

damping torque.

The dynamic model of incorporating the

hydraulic damper into the lower limb prosthetic

system is shown in Fig. 3. The lower limb prosthetic

system of the amputated patient can be simplified

Establishment and Simulation of the Damping Torque Model of Hydraulic Intelligent Knee Prosthesis

205

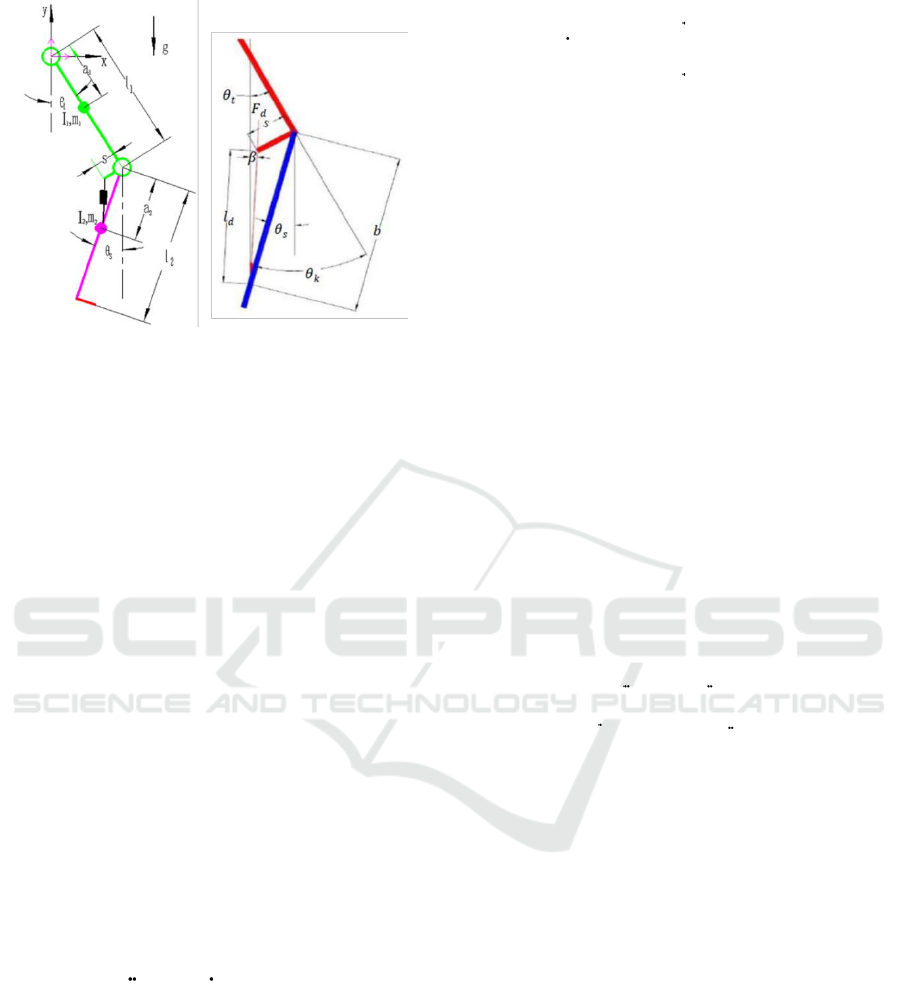
Figure 3. Dynamics model of lower limb prosthesis.

into a two rigid body model, which represents the

movement of the thigh and the calf in the sagittal

plane. The foot and leg tube are equivalent to a rigid

connection. In Fig. 3, subscripts 1 and 2 represent

the thigh and calf parameters respectively.

represents the mass.

represents the distance from

the centre of mass to the rotating joint.

represents the rotational inertia.



and



represent the angle between the thigh and the calf

and the vertical direction, respectively.



represents the knee angle.

represents the length

of the damper.

represents the distance between

the centre of knee rotation and the connection point

on the piston rod of the hydraulic damper.

represents the distance between the centre of knee

rotation and the joint point of the damper under the

leg tube.

represents hip torque.

Assuming that there is no friction between joints,

the second type of Lagrange equation is used to

establish the dynamic model (Xiaodong Wang et al.,

2015).

( ) ( + ( )D C G

    

  ，）

(2)

Inertial matrix is given by

1 1 2 1 2 1 2

2 1 2 2 2

cos( )

()

cos( )

ma m l m l a

m l a m a







   







  



(3)

Coriolis force and centrifugal force influence

coefficient matrix is given by

2 1 2

( ) sin( )

( , )

( ) sin( )

m l a

























(4)

Gravity torque parameter matrix is given by

1 1 2 1

sin( ) sin( )

()

sin( )

m a m l

















(5)

Hip and knee parameter matrix is given by

sin( )



















(6)

Thigh and calf angle vector matrix is given by











(7)

In the calculation of the dynamic equation of

lower limb movement, the hip torque and the thigh

angle produced by a normal person are known inputs.

Knee torque determined by Lagrange equation can

be expressed as follows:

2 2 1 2

2 1 2 2 2

cos( )

sin( ) sin

s t t s

t t s s s

a m l a

m l a m a

   

    



   



(8)

2.3 Hydraulic Damper Model

The hydraulic damper is a spring damper system. It

generates a real-time varying damping torque when

the knee prosthesis moves, so that the maximum

angle of the knee can be controlled at different

speeds to achieve physiological gait (Siyuan Gong et

al., 2010). The change of the hydraulic damping

torque is achieved by adjusting the opening of the

damper valve. The knee damping torque actually

generated by the hydraulic damper is given byx

( )L

  

(9)

is extension spring modulus, and

x

spring compression. Real-time moment arm length

can be expressed as follows:

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

206

cos( )

2 sin( )







  

(10)

Hydraulic damper pressure difference between

upper and lower chamber is

P

, and the effective

action area of the piston is

. Hydraulic damping

force can be expressed as follows:



(11)

Damper piston velocity is

. When hydraulic

oil flows through the valve, the effective flow area is

. Flow coefficient is

. And Hydraulic oil

density is



. So

P

can be expressed as follows:





(12)

The length of the damper

is a variable during

the movement. It can be expressed as follows:

2 sin( )

d s t

l b s



   

(13)

Damper piston velocity is given by

cos( )( )

2 sin( )







  

(14)

So the knee damping torque actually generated

by the hydraulic damper is given by

cos( )

()

2 sin( )







  

  

(15)

And then the knee damping torque actually

generated by the hydraulic damper can be expressed

as follows:

2 2 2

cos ( ).( )

()

2 ( 2 sin( )

cos( )

2 sin( )

s t t

d s t

C b s



  





  

  



  

(16)

Coupling the knee torque determined by the

kinetic equation with the torque provided by the

hydraulic damper is given by



(17)

When the knee geometric parameters and human

body parameters are determined, the hip and knee

angle information are measured and the real-time

valve flow area can be obtained. However, due to

the short time of a gait cycle, if the motor is used to

drive the valve to make the real-time change of the

area completely and track the matching theoretical

torque curve in actual operation, speed adjustment

will be too late and power consumption will be fast.

Therefore, the following simulation simulates the

actual torque curve and the theoretical torque curve

generated by several fixed flow areas at a walking

speed, and compares the analysis curve to determine

the most suitable flow area at this speed. The area

data is stored. And when the sensor detects the

walking speed of the wearer, the stored data can be

directly called.

2.4 Damper Torque Simulation

Using the hip and knee angle information of a

healthy person at a walking speed, the damping

torque curve required by the Lagrangian equation is

obtained by Matlab. The damping torque curve

actually provided by the hydraulic cylinder is

obtained by Matlab under the same conditions

different flow conditions, and then the best flow area

under this walking speed is obtained. In this

way, the optimal flow area under different walking

speeds is obtained in turn. The parameters of the

lower limb prosthesis system are designed as follows:

Figure 4. Hip angle input.

Establishment and Simulation of the Damping Torque Model of Hydraulic Intelligent Knee Prosthesis

207

Figure 5. Knee angle input.

9.9kg



2.6kg



0.55m



0.4m



0.267m



0.176m



0.031 .kg m



0.0032 .kg m



870 /kg m





5.37 10Am





0.185bm

0.02sm

0.7



1.4 10 /k N m

. The walking experimental data

of the normal person was obtained from the

literature (Matinmanesh & Mallakzadeh, 2011). And

the hip angle curve and the knee angle curve are

shown in Fig. 4 and Fig. 5, respectively.

The theoretical calculation of the knee joint

torque curve and the flow area

are respectively

taken

0.8 10 m





1.3 10 m





1.9 10 m





and the hydraulic damper actually provides the

torque curve as shown in Fig. 6.

It can be seen from the figure that under different

flow areas, the overall trend of the

Figure 6. Knee theoretical torque and damping torque in

different flow area.

hydraulic damping torque curve is consistent

with the theoretical torque curve. When

1.3 10 m





, the simulated knee torque is closest to

the theoretical torque curve. So this flow area can be

used as a preset flow area at this speed.

3 DISCUSSION

The torque required for the knee prosthesis at

different speeds are different. The control of the

knee damping torque is realized by the damper to

realize the tracking speed of the wearer. The

adjustment of the hydraulic knee damping force is

achieved by changing the flow area of the upper and

lower chambers of the hydraulic cylinder, and the

specific traveling speed corresponds to a specific

optimal flow area. As the flow area increases, the

damping force decreases nonlinearly. And when the

walking speed is constant, there is always a

corresponding optimal flow area. The theoretical

simulation results verify the correctness of the

kinetic model for knee damping torque control.

Since the modeling parameters are taken from

healthy people, the actual application will inevitably

produce a certain deviation. For specific lower limb

amputation patients, data from healthy people with

similar body size can be used as initial data for

prosthetic wearers. After the prosthesis is worn, the

angle information of the wearer's healthy leg and the

knee parameters are recalculated to obtain an

optimized opening degree.

4 CONCLUSIONS

In this study, a dynamic model of the lower limb

prosthetic system was established by designing an

intelligent knee joint structure. The coupling of the

hydraulic damper and the system dynamics model is

used to determine the flow area of the knee damping

torque. The Matlab-based simulated damping torque

curve is compared with the theoretical curve to

determine the knee damper opening at the tester's

specific speed. The following results are obtained

from the simulation:

(1) The relationship between hydraulic damping

and flow rate determines its superiority for knee

joint damping torque control. The hydraulic

damping torque curve can be obtained by changing

the flow area of the valve. By comparing and

analyzing the theoretical knee torque curve and the

hydraulic damping torque curve, the optimal flow

area at a specific speed can be obtained.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

208

(2) As the flow area increases, the knee joint

damping torque gradually decreases. The optimal

flow area at different speeds can be simulated

multiple times by using the measured hip and knee

angle curves as input data.

(3) The knee damping torque curve under the

optimal flow area obtained by the simulation has a

small deviation from the theoretical curve, but the

change trend is basically consistent with the

theoretical curve. The correctness of the kinetic

model is verified and can be optimized by replacing

the data of healthy people with the wearer's own

measured data.

REFERENCES

Chunxia Zhao, Ting Liu, et al., 2015. Design and

evaluation of an overall unloading knee brace. Journal

of Medical Biomechanics 30(6): 564-568.

Dundass C., Yao, et al., 2003. Initial Biomechanical

Analysis and Modeling of Transfemoral Amputee Gait.

Jpo Journal of Prosthetics & Orthotics 15(1):20-26.

Dabiri Y., Najarian S., et al., 2009. Passive Controller

Design for Swing Phase of a Single Axis Above-Knee

Prosthesis. Iranian Journal of War & Public Health

1(3):76-87.

Furse A., Cleghorn W., Andrysek J., 2011. Development

of a low-technology prosthetic swing-phase

mechanism. Journal of Medical & Biological

Engineering 31(2):145-150.

Hongliu Yu, Jiahua Hu, et al., 2010. Dynamics modelling

of artificial legs system based on knee joint damper

characteristics. Journal of Machine Design 27(2):40-

42.

Hongliu Yu, Ling Shen, et al,.2009. Design of electro-

nically controlled hydraulic damper for prosthetic

knee. Journal of Clinical Rehabilitative Tissue

Engineering Research 13(39):7635-7638.

Kun Shang, Lixing Shen, et al., 2009. Realization of

kinematics simulation software for four-bar artificial

limb knees. Journal of Medical Biomechanics 24 (2):

107-111.

Matinmanesh A., Mallakzadeh M., 2011. Inverse kinetic

and kinematic analysis of drop-foot patient's walking.

E-Health and Bioengineering Conference (EHB).

IEEE, 2011:1-4.

Suzuki Y., 2010. Dynamic optimization of transfemoral

prosthesis during swing phase with residual limb

model. Prosthetics & Orthotics International

34(4):428-38.

Staros A., Murphy E.F., 2013. Properties of fluid flow

applied to above-knee prostheses. Journal of

Rehabilitation Research & Development 50(3): XVI-

XVI.

Siyuan Gong, Peng Yang, et al., 2010. Development of

intelligent lower limb prostheses based on iterative

learning control: A follow of normal walking speed.

Journal of Clinical Rehabilitative Tissue Engineering

Research 14(13):2295-2298.

Tengyu Zhang, Yubo Fan, 2016. Motion recognition based

on EMG signals of residual limb in transfemoral am-

putee. Journal of Medical Biomechanics 31(6).

Tahani M., Karimi G., 2010. A New Controlling

Parameter in Design of Above Knee Prosthesis. World

Academy of Science Engineering & Technology,

2010(70):926.

Unal R., Carloni R., Hekman E.E.G, et al., 2010. Bio-

mechanical conceptual design of a passive

transfemoral prosthesis. Conf Proc IEEE Eng Med

Biol Soc 2010(10):515-8.

Wujing Cao, Hongliu Yu, et al., 2016. Research on intel-

igent knee joint control method based on different

signal sources. Chinese Journal of Rehabilitation

Medicine 31(10):1129-1132.

Xiaodong Wang, Chunhui Wang, et al., 2015. Bio-

mechanical simulation model of upper limb interaction

for human-spacesuit system. Journal of Medical

Biomechanics 30(6): 540-546.

Yanli Geng, Peng Yang, et al., 2013. Data acquisition and

motion simulation of lower limb. Journal of Medical

Biomechanics 2013, 28(2).

Establishment and Simulation of the Damping Torque Model of Hydraulic Intelligent Knee Prosthesis

209