
Dynamic Error Compensation Model of Articulated Arm Coordinate
Measuring Machine
Jiaqi Zhu
1, a
, Xugang Feng
1, b, *
and Jiayan Zhang
1, c
1
School of Electrical and Information Engineering, Anhui University of Technology, Ma’anshan 243032, China
Keywords: Neural network, Simulated annealing algorithm, Flexible arm coordinate measuring machine, Error
compensation.
Abstract: The error factors of articulated arm coordinate measuring machine (AACMM) are many and the
relationship between them is nonlinear, which is difficult to establish the model by traditional mathematical
modeling. This paper analyses the error sources, on the basis of parameter calibration, to select the angle
coding, thermal deformation and probe system as the research object and introduce coordinate values to
indirectly describe the remaining errors in the model. The BP neural network is used to build up the error
compensation model, connection weights of the neural network are optimized by the modified simulated
annealing (MSA) algorithm, which solves the problem that the neural network is easy to fall into the local
minimum and the susceptible to interference. The data samples are obtained through experiments, and the
test data are utilized to exercise model built. The experimental result demonstrates that the average value of
the single point repeatability error after compensation is reduced from 0.1782 mm to 0.0383 mm.
1 INTRODUCTION
The articulated arm coordinate measuring machine
(AACMM) generally having 6 degrees of freedom is
a non-orthogonal coordinate system measuring
device that simulates the structure of the human arm.
It has broad application prospects, not only can
complete online measurement and evaluation on the
assembly line, but also suitable for outdoor
measurement and occasions where the object tested
is inconvenient to move. The advantages involves of
easy portability, low price, flexible measurement,
large measuring range and practicality in the field.
Due to its series-space open-chain structure, the
measurement error has the characteristics of
accumulation, transmission and amplification during
the measurement process, ultimately leading to poor
overall performance of the measuring machine (Zhao
H N, Yu L D, Jia H K, et al, 2016; Feng X G, Xu C,
Zhang J Y, et al, 2016; Fedorov V G, 2008; Romdhani F ,
François Hennebelle, Ge M , et al, 2015; Xing H L, Bo C,
Zu R Q, 2013).
At present, the AACMM mainly reduces the
error by calibrating the structural parameters
according to calibration algorithm or external high-
precision equipment. For example, Santolaria J et al
established an error model based on Fourier
polynomial and estimated the parameter error of the
AACMM machine by using a spherical gauge with
14 spheres (SANTOLARIA J., AGUILAR J.J. YAGUE
J.A., et al, 2008). ACERO studied the feasibility of
laser tracker as a reference instrument in AACMM
parameter calibration (ACERO R., BRAU A.,
SANTOLARIA J., et al, 2015). Zheng D T established
the spatial point error model and spatial error
distribution of the AACMM by using the basic
theory of functional network and the principle of
vector machine (Zheng D T, FEI Y T, 2010).
However, there are many error factors in the
AACMM, and the structural parameters are only a
part of it. This paper analyzes the error sources in
the measurement space and applies a method based
on the improved simulated annealing algorithm to
optimize the neural network to model the multiply
error of the coordinate measuring machine. By
comparing the results, the validity of the
compensation model is verified.
2 ERROR ANALYSIS
The AACMM is composed of three joint arms and
one probe combined through six rotary joints in
210
Zhu, J., Feng, X. and Zhang, J.
Dynamic Error Compensation Model of Articulated Arm Coordinate Measuring Machine.
DOI: 10.5220/0008856502100216
In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 210-216
ISBN: 978-989-758-412-1
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

series. The structure diagram is shown in Figure 1
(Zheng D T, Fei Y T Zhang M, 2009; Cao Q S, Zhu J,
Gao Z F, et al, 2010).
Figure 1. Schematic diagram of the AACMM.
The classical mathematical model describing the
transformation relationship of adjacent members is
the D-H model.
Due to the seventh coordinate system is centered
on the probe , translated by the sixth coordinate
system, the center of the probe is coordinated in the
6 6 6
,,x y z
coordinate system is
( , , )
x y z
B B B
, and
the coordinate transformation matrix B is
T
zyx
BBBB 1
, so the spatial position
coordinates of the probe relative to the base
coordinate system is:
6
1
1
p
p
i
i
p
x
y
AB
z
6
1
cos sin cos sin sin cos
sin cos cos cos sin sin
0 sin cos
0 0 0 1 1
i i i i i i i x
i i i i i i i y
i
i i i z
lB
lB
dB
(1)
According to formula (1), the coordinate value of
the probe depends on the joint angle
, the torsion
angle
, the joint length
l
and the joint offset
d
when the probe parameters are not considered
(
Santolaria J , José-Antonio Yagüe, Roberto Jiménez, et al,
2009; Markov B N, Sharamkov A B, 2014
). There are a
total of 24 structural parameters. The nominal values
of the structural parameters on the D-H model in this
paper are shown in Table 1 But this is a static error
in the AACMM, there are some additional errors
usually generated in the measurement process
(
ZHANG T, DU L, DAI X, 2014
). Thus, the error
source of the measurement process of the measuring
machine needs to be analysed.
Table 1. Nominal value of structural parameters.
Joint
0i
(rad)
(rad)
l
(mm)
d
(mm)
1
0.111
-90..942
40.855
349.521
2
0.424
90.273
-40.562
0.723
3
-0.103
-89.821
24.588
269.051
4
-0.076
89.853
-23.877
0.812
5
0.873
-90.165
23.935
240.364
6
-0.225
90.453
-24.168
-0.162
The mainly following error sources are as follow.
(1) Thermal deformation error, caused by
internal and external heat sources, resulting in errors
caused by arm length, circular grating and thermal
deformation of joint components. (2) The probe
system error, divided into the radius cosine error of
the contact probe and the error caused by the optical
probe failing to accurately detect. (3) Measuring
force error, mainly caused by the contact
measurement force generated by the contact probe,
which causes the error caused by the bending
deformation of the measuring rod. (4) Angle coding
error, due to the accuracy of the angle encoder itself
and the error caused by assembly deviation. (5) The
point error of the measurement space, because the
AACMM has its optimal measurement area, the
measurement is made in different measurement
areas and the error caused by the difference of the
position of the joint arm. (6) Data acquisition system
error, due to errors caused by electromagnetic
interference, data acquisition delay and its own
unreliable data acquisition system in the AACMM.
(7) Motion error, caused by bearing sway and
unstable parts due to accuracy problems in
component manufacturing and assembly in the
measurement process (8) improper manual operation
errors.
Through the above analysis, the AACMM is a
complex system with multiple error sources. For the
structural parameter error, the static parameters can
be calibrated by the calibration system or the
calibration algorithm. However, if all the error
factors are all using the calibration method, the
calculation process would be too complicated and
easy to generate quadratic error. In order to better
solve the influence of the remaining errors in the
space and improve the measurement accuracy of the
Dynamic Error Compensation Model of Articulated Arm Coordinate Measuring Machine
211

AACMM, this paper mainly deals with the
following error factors in the measurement process,
which consist of thermal deformation error, angle
coding error, probe system error. The temperature of
the heat deformation is affected by the internal and
external heat sources, and 8 thermal monitoring
points are placed. 7 temperature sensors are placed
on the measuring machine, and the other is the
ambient temperature monitoring point. Due to the
temperature characteristics, it is necessary to wait
for a certain time to make the environment and the
measuring machine reach the thermal balance during
the experiment. The measuring head of the
AACMM studied in this paper is a contact probe;
there are 2 types of probe systems used in the
experiment. The specific parameters are shown in
Table 1. Each probe is measured the same number of
times. For measurement area errors, the data samples
of the measuring machine need to be measured
multiple times at different locations. The influence
of the measurement force error is small and it is
difficult to obtain the pressure value when
measuring the cone, which is combined with the
other random errors indirectly described by the
coordinate values in the model.
Table 2. Parameters of the probe system.
number
diameter
/mm
Material
X
/mm
Y
/mm
Z
/mm
1
4
ruby
0
0
50
2
3
ruby
0
0
40
3 MODEL
3.1 BP Neural Network
BP neural network (BP) can be regarded as a highly
nonlinear mapping from input to output, and has
excellent comprehensive processing capability
Aiming at the problem that the AACMM has
complicated error sources and the relationship
between them is nonlinear, BP neural network is
used to model the error of the AACMM to establish
a 3-layers network with input layer, hidden layer and
output layer. Based on the above analysis, there are a
total of 18 neurons in the input layer, which are 6
joint angle values, the temperature of 6 joints,
pedestal and the measurement space, the system type
of touch probe, and the measuring coordinate value
x, y, z; the number of neurons in the output layer is
determined to be 3, respectively, is error values for
the x-axis, y-axis, and z-axis; the number of neurons
in the hidden layer is set to 2×18+3=39 according to
the Kolmogorov theorem, and the transfer function
uses the S-type tangent function. Therefore, the
structure of the BP neural network used is 18-39-9,
shown in Fig. 2. The weight value of the network is
18×3 9+39+39×3+3=861.
For the 3-layer neural network, the neurons in
the input layer are responsible for receiving the input
information and transmitting it to the neurons in the
hidden layer; the hidden layer is the internal
information processing layer, duty for information
transformation; the output layer is responsible for
outputting the information of each neuron. In the
process of forward propagation, x is the neural
network input, y is the neural network output, w is
the weight,
is the neural network bias, and f is the
excitation function. The relationship between input
and output is:
The input of hidden layer:
1
n
k uj j
j
net w x
(2)
The output of hidden layer:
jk
y f net
(3)
The input of output layer:
1
n
k uj j
j
net w x
(4)
The output of output layer:
kk
y f net
(5)
During the learning process, the neural network
repeatedly adjusts the weights and thresholds of the
network based on empirical results, which is
accomplished by minimizing an objective function:
2
11
1
ml
uj uj
uj
E Y y
m
(6)
Where:
uj
Y
is the actual output of the jth neuron,
uj
y
is the predicted output of the jth neuron, and m
is the number of training samples.
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
212

hidden layer output layer
X-axis error
Temperature value1
Temperature value3
Probe system type
u
j k
input layer
Temperature value2
Y-axis error
Z-axis error
Figure 2. Model Structure of Neural Network
In the process of feedback, the formula of the
gradient descent method when the weight is
modified is:
uj uj uj
w w E w
(7)
Where:
is the step size,
uj
Ew
is the
partial derivative of the objective function.
3.2 Modified Simulated Annealing
Algorithm
The Simulated Annealing Algorithm (SA) is derived
from the annealing process of solid matter in
simulated physics. It is an optimal solution for
finding propositions in a large search space within a
certain period of time, decomposed into three parts
of solution space, objective function and initial
solution. Starting from setting a higher initial
temperature, a new solution is generated for the
initial solution random disturbance and substituted
into the energy function to determine whether the
Metropolis criterion is met. If the new solution can
be accepted by the system, the 'cooling' process is
performed to generate the next new solution.
According to the cooling coefficient, the temperature
is reduced to minimize the energy function, and the
global optimal solution can be obtained by receiving
the temporarily deteriorated solution to jump out the
local optimal "trap".
However, when SA solves nonlinear multiple
parameters, the number of solutions and the solution
space range is too large to make the convergence
slow, and the temperature reduction in the
calculation process further reduces the calculation
efficiency. Thus, this paper adopts an improved
simulated annealing algorithm: one is to preserve the
intermediate optimal solution that can be updated in
time during the algorithm search process; the second
is to reduce the search range when the algorithm is
close to the optimal solution to improve search
efficiency and accuracy. To determine that the
current state is close to the optimal solution, the
following two conditions must be satisfied:
(1) The current repeatability
RP
is less than
the set value
; (2) The previously calculated
repeatability
RP
is not significantly improved,
meaning
RP
is less than the set value
.
3.3 MSA-BP Model
It can be seen from the above description that the BP
neural network is essentially an unconstrained
nonlinear optimization process. Its learning rule is to
use the descent algorithm to modify the weight
through the negative gradient direction of the error
function to minimize the sum of squared errors of
the network, which has the disadvantages of slow
convergence speed and weak anti-interference
ability and easy to fall into the local minimum state.
The modified annealing algorithm is used to
optimize the initial weight of the BP neural network,
stopping when the formula (7) is calculated to meet
the set accuracy or reached the set maximum
number of iterations. to obtain the optimal weight of
the neural network and overcome the shortcomings
of the BP neural network.
The algorithm steps are as follows:
(1)A part
Step 1: Set multiply parameters: initial
temperature
0
T
, initial weight
0
=
0
, terminate
test accuracy
e
, terminate temperature
min
T
, the
Dynamic Error Compensation Model of Articulated Arm Coordinate Measuring Machine
213
threshold of checking sampling stability
N
,
algorithm switch parameters
and
, make the
initial optimal solution
0
, the number of
iterations
0i
, search range delta=delta-L;
Step 2: Let
i
TT
, call the B algorithm with
T
,
and
i
as parameters, and return the state
to the current state(mean
i
=
) by the B
algorithm, update
;
Step 3: Cool down
1ii
T T T
,
1ii
;
Step 4: If
min
TRP or Te
, go to step 5; if
RP and RP
, then let delta = delta-S
(delta-S < delta-L), and turn to step 2;
Step 5: Output the final optimal solution
*
,
abort the algorithm.
(2)B part
Step 1: Set the initial structural parameter
0 i
when
0k
, and the initial optimal
solution is
.
Step 2: Generate a new solution by
*k rand delta
and calculate
RP RP RP k
, where rand is a
random number of the interval [-1, 1], in accordance
with the Cauchy distribution;
Step 3: If
0RP
, then
1k
,
;
if
0RP
, calculate the acceptance probability
exp /r RP T
, if
r pp
, then
1k
,
otherwise,
1kk
pp is the random number
on the interval [0, 1];
Step 4:
1kk
, If
kN
, go to step 5,
otherwise turn to step 2.
Step 5: Return the current optimal solution
and current state
1k
to the A algorithm.
4 EXPERIMENTAL
A standard rod where the length between cone-shape
holes is 322.63 mm is placed at eight different
positions in the measurement area of the AACMM.
After setting several temperature ranges, AACMM
starts measuring when the temperature field of the
machine to be measured reaches the thermal
equilibrium. The AACMM should adopt different
positions while sampling the data, and the pose of
length rod can by operating rotate platform in the
measurement space. A total of 800 sets of data were
measured, where 700 sets of it are randomly selected
as the training data of the neural network. When
randomly selection, the two sets of data on the rod in
the same position are not separated, and the
remaining 100 sets of data are used as test data to
verify the predictive effect of the proposed neural
network model.
In order to verify the compensation effect of the
MSA-BP model, after the neural network training to
reach the end condition, the 100 sets of test samples
are corrected to calculate the measurement errors
before and after the compensation.
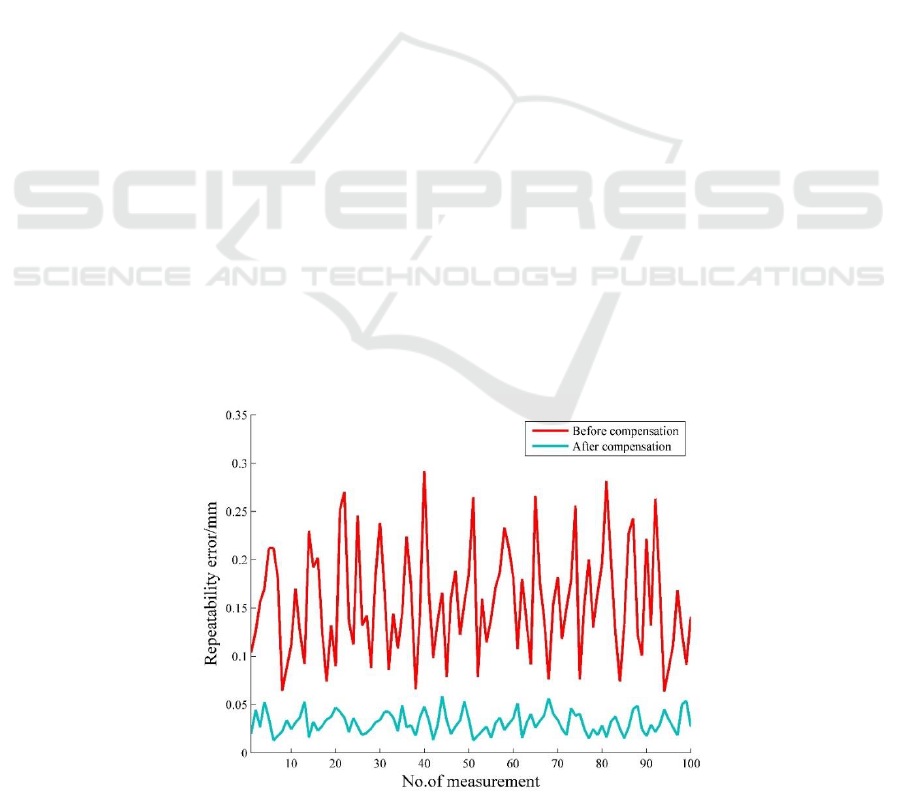
Figure 3. Repeatability error of the single cone-shape hole before and after compensation.
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
214
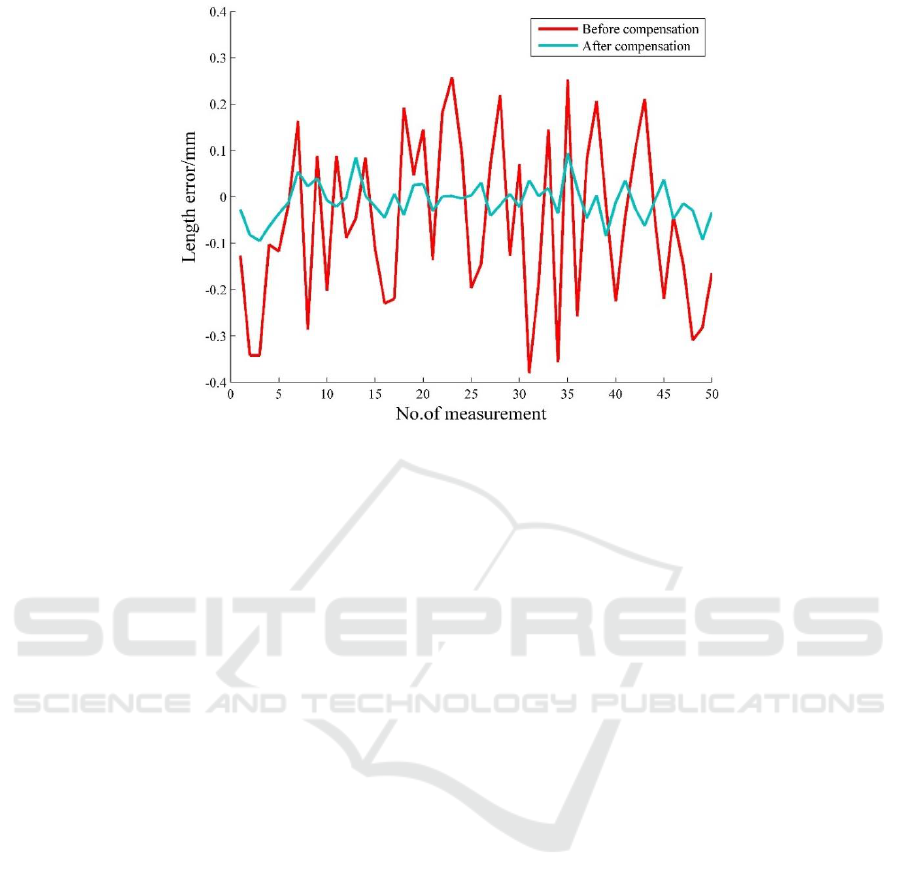
Figure 4. Length measurement errors before and after compensation.
Figure 3 shows the single point repeatability
error before and after model compensation. Let the
average of each set of measurement data be the true
value. It can be seen from the figure that the average
value of the single point repeatability error using the
AACMM is 0.1782 mm, and the average value of it
after the dynamic model compensation is 0.0383
mm. Figure 4 is a length measurement error diagram.
The average length measurement error is reduced
from -0.0681 mm m (before compensation) to -
0.0085 mm (after compensation).
5 CONCLUSION
The source of measurement error of the AACMM is
analyzed, due to the lack of the unified error
calculation formula, a dynamic error compensation
method based on MSA-BP for AACMM is proposed.
The BP neural network is used as the error
compensation model of the AACMM, the weight of
which is optimized by adopting the modified
simulated annealing algorithm, which improves the
convergence speed and operation efficiency. The
simulation results show that the average value of the
repeatability error based on the parameter calibration
is 0.1782mm. After compensation of the MSA-BP
model, the average value of the repeated error is
0.0383mm. The dynamic error compensation model
presented in this paper can effectively improve the
accuracy of the AACMM and has good engineering
application value.
ACKNOWLEDGEMENTS
This paper was supported by Anhui Natural the
Science Foundation (No.1908085ME134), by Anhui
Key Research and Development Plan Project
(No.1804a09020094) and by the key research
project of Natural Science in Anhui University
(No.KJ2018A0054, KJ2018A0060).
REFERENCES
ACERO R., BRAU A., SANTOLARIA J., et al.
Verification of an AACMM using a laser tracker as
reference equipment and an indexed metrology
platform[J]. Measurement, 2015, 69: 52- 63.
Cao Q S, Zhu J, Gao Z F, et al. Design of Integrated Error
Compensating System for the Portable Flexible
CMMs[M]// Computer and Computing Technologies
in Agriculture IV. Springer Berlin Heidelberg,
2010:410-419.
Fedorov V G. Six-axis coordinate measuring machines [J].
Measurement Techniques, 2008, 51(7):724-725
Feng X G, Xu C, Zhang J Y, et al. The establishment and
testing of a model called virtual AACMM [J]. Journal
of Chongqing University, 2016, 39(06):135-140.
Markov B N, Sharamkov A B. The Use of the Results of
Calibration of Faro Arm Coordinate-Measuring
Machines for Use in Comparative Estimation of Their
Precision Capabilities [J]. Measurement Techniques,
2014, 57(8):870-874.
Dynamic Error Compensation Model of Articulated Arm Coordinate Measuring Machine
215

Romdhani F, François Hennebelle, Ge M, et al.
Methodology for the assessment of measuring
uncertainties of AACMMs [J]. Measurement Science
& Technology, 2015, 25(25):125008.
SANTOLARIA J., AGUILAR J.J.,YAGUE J.A., et al.
Kinematic parameter estimation technique for
calibration and repeatability improvement of
AACMM[J]. Precision Engineering, 2008, 32(4): 251-
168.
Santolaria J, José-Antonio Yagüe, Roberto Jiménez, et al.
Calibration-based thermal error model for AACMMs
[J]. Precision Engineering, 2009, 33(4):476-485.
Xing H L, Bo C, Zu R Q. The calibration and error
compensation techniques for an Articulated Arm
CMM with two parallel rotational axes [J].
Measurement, 2013, 46(1):603-609.
ZHANG T, DU L, DAI X. Test of Robot Distance Error
and Compensation of Kinematic Full Parameters [J].
Advances in Mechanical Engineering, 2014, 2014
(22):1-9.
Zhao H N, Yu L D, Jia H K, et al. A New Kinematic
Model of Portable Articulated Coordinate Measuring
Machine [J]. Applied Sciences, 2016, 6(7):181.
Zheng D T, FEI Y T. Research on Spatial Error Model of
Flexible Coordinate Measuring Machine [J]. Journal
of Mechanical Engineering, 2010, 46(10):19-24. (In
Chinese)
Zheng D T, Fei Y T Zhang M. Research on functional
networks of flexible coordinate measuring machine
modelling [J]. Journal of Electronic Measurement and
Instrument, 2009, 23(04): 33-37. (In Chinese)
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
216
