Detection System Design of the Glenohumeral Joint Motion

Information

Jianfeng Li

1, a

, Chunzhao Zhang

1, b

and Qiang Cao

1, c

College of Mechanical Engineering and Applied ElectronicsTechnology, Beijing University of Technology, No.100

Pingleyuan, Beijing, China

Keywords: Detection system, Detection mechanism, Measurement system, Glenohumeral joint motion information.

Abstract: Due to the complex coupled motion of shoulder mechanism, design the guiding movement rule of

rehabilitation robot generally lack of the glenohumeral (GH) joint motion information. This study focused

on development detection system design of the GH joint motion information. In this paper, the detection

system incorporates the detection mechanism and measurement system. Design of the detection mechanism

includes model of the shoulder complex, configuration as well as structure design of the detection

mechanism. Design of the measurement system includes hardware selection and software development.

Straight after, detection system was integrated. Then, test and analysis was presented. The results show the

detection system can measure and present the GH joint motion information in real time. It provides a

method to obtain the movement information of the GH joint, and has practical significance for shoulder

function simulation and ergonomics.

1 INTRODUCTION

With the aggravation of aging and traffic accidents

happen frequently, more and more patients with

upper limb motor dysfunction. To repair upper limb

injury, rehabilitation training equipment is more and

more popular. Due to most of the joints movements

of the upper limb need to be based on the

glenohumeral (GH) joint motion, obtainment the GH

joint motion information is very important to design

the structure of upper limb rehabilitation training

equipment and is of practical significance to ensure

the rehabilitation training effect of the affected limb

(Kirsch, 2001; Kiguchi, 2011).

The GH joint is one of the joints in the shoulder

complex and the shoulder complex is an especial

complicated and correlative system ( Tobias, 2009),

which results in extremely complex GH joint

movement. Although many researchers have studied

the coupled motion of the shoulder complex, only a

small amount of quantitative information on the GH

joint is available in the existing literature (Yang,

2005). Thus, to find a method to quantize the daily

movement information of the GH joint is necessary.

In this paper, the motion information detection

system of the GH joint is developed, which provides

a method to obtain the movement information of the

GH joint, and can obtain and present the GH joint

motion information in real time.

2 DETECTION SYSTEM DESIGN

2.1 Model of the Shoulder Complex

To obtain the motion information of the GH joint, it

is necessary to understand the shoulder complex due

to the GH joint is one of the joints in the shoulder

complex. Generally, the shoulder complex consists

of the shoulder girdle and the humerus, and the

humerus connects to the scapula of shoulder girdle

through the GH joint (Klopčar, 2006). The shoulder

girdle includes three bones (the scapula, sternum,

and clavicle) and three joints (the sternoclavicular

(SC), scapulothoracic (ST), and acromioclavicular

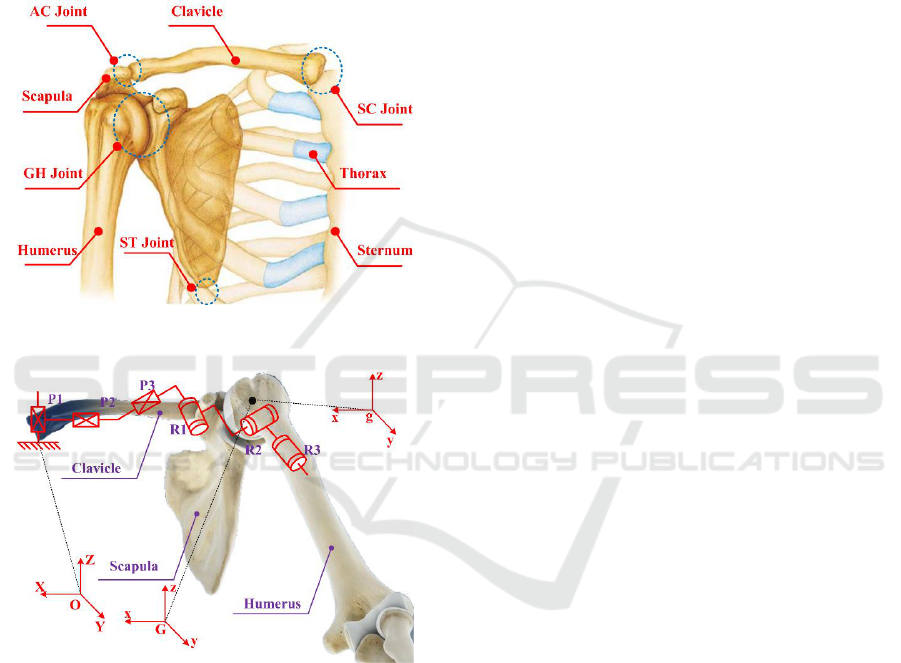
(AC) joints). As shown in Figure. 1. The GH joint is

composed of the humeral head and the glenoid

cavity of the scapula, which is usually equivalent to

a spherical joint, and the kinematics of the AC, ST,

and SC joints are not clear (Yang, 2005); Thus, it is

difficult to understand the motion characteristics of

the GH joint relative to the sternum.

222

Li, J., Zhang, C. and Cao, Q.

Detection System Design of the Glenohumeral Joint Motion Information.

DOI: 10.5220/0008867702220226

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 222-226

ISBN: 978-989-758-412-1

Theoretically, all of the joints and bones of the

shoulder complex that exhibit 6-degree of freedom

(DOF) are particularly complex. Practically

speaking, some researchers, who are just looking for

an equivalent kinematic structure considering the

overall motion characteristics, do not wholly

replicate the shoulder complex. The mechanistic

theory of joint physiology is helpful for

understanding the shoulder complex kinematics

(Maurel, 2000; Lenarčič, 2006; Tondu, 2006).

Figure 1. Anatomy of the shoulder complex.

Figure 2. Mechanism model of the shoulder complex.

For the GH joint has three revolute DOFs with

the axes intersecting vertically in the GH joint center

as well as moves with the functional relevance of the

shoulder girdle during humeral movements and

according to the knowledge of theoretical mechanics,

the general motion of a rigid body can be

decomposed into translation following any of the

base points and rotation relative to the base point.

Thus, the shoulder girdle is assumed to be a platform.

The mobile reference frame is established on the

shoulder girdle, and the origin of the mobile

reference frame is G. Relative to the global

coordinate system: O-XYZ, the G point has three

translational DOFs. The fixed connection coordinate

frame is established on the humerus head, and the

origin, represented by g is a point on the humerus

head coincident with the GH joint center. Relative to

the mobile reference frame, the humerus has three

rotational DOFs with the axes intersecting vertically

in the g point in space. In this way, a generalized GH

joint with floating center (i.e., a 3-DOF spherical

joint with floating center, whose center displacement

variable relative to the sternum is coupled with its

rotation) has been presented, as shown in Figure. 2.

2.2 Detection Mechanism Design

2.2.1 Mechanical Analysis of DOF

According to the model of the shoulder complex, the

GH joint possesses six DOFs (three rotation and

three translation). In order to completely track the

GH joint, the detection mechanism possess three

vertical orthogonal translational joints and three

rotational joints with the axes intersecting vertically

in GH joint center. From the view of the theory of

mechanism, the DOF of the detection mechanism

meets the requirements.

2.2.2 Structure Design of the Detection

Mechanism

The self-tracking mechanical system includes

horizontal tracking mechanism, vertical tracking

mechanism that includes a pulley mechanism, and

wearing mechanism, which are presented in figure. 3.

The function of the self-tracking mechanical system

can be able to fully track the motion information of

the GH joint. The following are the description of

horizontal tracking mechanism, vertical tracking

mechanism, and wearing mechanism in details.

Horizontal tracking mechanism poses two DOFs,

which is mounted on the support plate. It consists of

two interconnected guide strip slide mechanism

which are equivalent to prismatic joints and tracks

the GH joint displacement variable in the horizontal

plane(two guide strip slide mechanism has sufficient

range of motion to track the horizontal motion of the

GH joint).

Vertical tracking mechanism poses one DOF,

which is mounted on the horizontal mechanism. It

consists of one guide strip slide mechanism and a

pulley mechanism. The guide strip slide mechanism

tracks the GH joint displacement variable in the

vertical axis direction, which has sufficient range of

motion to track the vertical axis direction motion of

Detection System Design of the Glenohumeral Joint Motion Information

223

the GH joint. The pulley mechanism can balance the

gravity of the vertical guide strip slide mechanism.

Horizontal

tracking

Wearing

mechanism

Vertical

tracking

Pulley

mechanism

Pulley

mechanism

Glenohume

ral joint

center

Wear

mechanism

Figure 3. Detection mechanism

Wearing mechanism has three revolute DOFs

with the axes intersecting vertically in the GH joint

center, which is mounted on the vertical mechanism.

It consists of three revolute joints which are

connected to each other and is to track three-

dimensional rotation of the GH joint.

2.3 Measurement System Design

Figure. 4 is the measurement system schematic

diagram, which includes the hardware and software.

Detection object

Displacemen

t sensor

Incremental

encoder

Signal

adjustment

module

USB

6341

Ordinary ComputerLABVIEW

Figure 4. Diagram of measurement system

2.3.1 Hardware of the Measurement System

The hardware mainly includes three displacement

sensors (NS-WY-02), three incremental encoders

(CFZ2124-3600-06-14F), signal adjustment module,

and a collection card of NI-USB-6341. The function

of the displacement sensor is to obtain the

displacement variable of the GH joint in three

dimensions. The incremental encoder is to obtain the

angle motion information of the GH joint during

humerus rotation movement. The signal adjustment

module is to adjust the weak signal of the sensors

and the incremental encoders. The NI-USB-6341 is

to obtain the adjustment signal which can be

transmitted to the ordinary computer via USB port,

the actual components are presented in figure. 5.

Figure 5. Diagrams of components

2.3.2 Software of the Measurement System

The displacement sensor outputs voltage signal and

the encoder outputs digital signal. Thus, this

detection system needs to detect three channels of

analog voltage signals, three channels of digital

signals, and the six channels of signals are required

for synchronous acquisition. The collecting

information of the three encoders use three counters

as well as the information of the three displacement

sensors and synchronous acquisition is a

conventional collection.

Using LABVIEW to develop the underlying

application, specific programming principle is as

follows: First of all, establishment three-way analog

input channels collect voltage signal and

establishment a three-way counter signal acquire

encoder Angle. Using the data line of the error

message to arrange the parallel execution sequence

and the counter to synchronize the trigger signal.

The analog input channel and counter acquisition

channel are set to the same sampling rate and

synchronization trigger counter clock source, so as

to realize synchronization of all signal acquisition.

2.4 Detection System Integration

Combined with the data measurement system

described in the above section, the rotation

information of the GH joint can be obtained through

the connection of the encoder, coupling, and the

detection mechanism; the translation information of

the GH joint can be acquired through the connection

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

224

of the displacement sensor and the detection

mechanism. Then, the GH joint motion information

detection system is obtained.

Figure 6. System integration.

The whole system starts from the tested object

and converts it into electrical signal through the

sensor and encoder. After the signal conditioning

module, the signal is sent to the data acquisition card

(NI-USB-6341) for collection and then process by

the software. The data curve in the acquisition

process is displayed on the monitor in real time. The

structure diagram of measurement system and

detection system integration is shown in figures. 4, 6.

3 TEST AND ANALYSIS

The prototype of the detection system is shown in

Figure. 6. At the beginning of the test, the tester

weared the detection mechanism and the

experimenter made the wearing device's three

rotational joints with the axes intersecting vertically

in GH joint center. Then, the tester rotated humerus

complete the flexion and extension movement in

five cycles, and the detection system presented and

recorded the GH joint motion data. One set of data

was described below: Tester (age 26 years; height

179 mm; weight 82kg; arm length 551.5mm) made

humerus complete the flexion/extension movement

in five cycles. Experimental results, which are the

GH joint motion data during flexion/extension

movement in five cycles, are shown in Figure.7.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Cycle(%)

Adduction and abduction angle(°)

Moving average Data point

(a)

-20

100

120

140

160

Cycle(%)

Flexion and extension angle(°)

Moving average Data point

(b)

-0.5

Moving average Data point

Cycle(%)

Internal and external angle(°)

0.5

1.5

2.5

(c)

-10

Cycle(%)

X Displacement variable quantity(mm)

Moving average Data point

-5

(d)

Detection System Design of the Glenohumeral Joint Motion Information

225

Moving average Data point

-10

-5

-15

Y Displacement variable quantity(mm)

Cycle(%)

(e)

Cycle(%)

Z Displacement variable quantity(mm)

Moving average Data point

-10

(f)

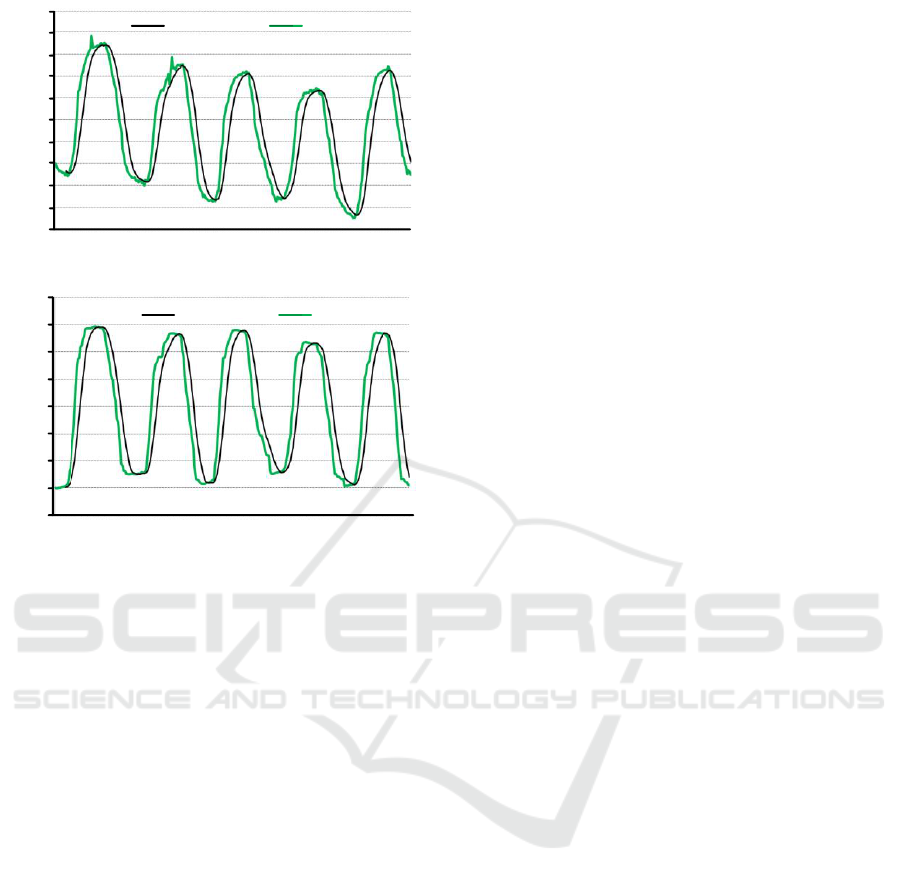
Figure 7. Diagrams of the GH joint motion information

relative to the sternum during humeral natural flexion and

extension rotation in five cycles: (a) humeral adduction

and abduction rotation angle, (b) humeral flexion and

extension rotation angle, (c) humeral internal and external

rotation angle, (d) X of the GH joint displacement variable,

(e) Y of the GH joint displacement variable, (f) Z of the

GH joint center displacement variable.

Fig. 7 shows the green curves (black lines is the

moving average) for the tester performing humerus

flexion/extension nature movement in five cycles

and the angle range is about 120°. The movements

of the GH joint in three dimensionsin

(adduction/abduction, flexion/extension, and

internal/external) and the GH joint center

displacement variable in the X, Y, and Z directions

are observed, which are presented in (a), (b), (c), (d),

(e), and (f), respectively. During the nature

flexion/extension movement of the humerus, a small

amount of adduction as well as abduction and

internal as well as external movement occurs with

the lifting process. This phenomenon is normal

during the natural flexion/extension movement of

the humerus, because it is impossible for the

humerus lifting process to completely guarantee in

the sagittal plane. However, the GH joint center

displacement variable large and regular in the X, Y,

and Z directions confirmed the coupled motion of

the shoulder complex. Subsequently, a great deal of

tests and analyses were performed, the above similar

results are also presented.

4 CONCLUSIONS

In this paper, a kinematic model of the shoulder

complex (3-DOF GH joint with floating center) was

proposed. Then, a detection system was designed.

Real-time GH joint motion information was

obtained, which confirmed the rationality of the

shoulder complex model and detection system.

It provides a method to obtain the movement

information of the GH joint and the detection system

can obtain the fundamental motion data of human

shoulder motion. Which has practical significance

for shoulder function simulation and ergonomics.

ACKNOWLEDGEMENTS

This work was supported by the National Natural

Science Foundation of China under Grants No.

51675008 and No. 51705007, the Beijing Natural

Science Foundation under Grants No. 3171001 and

No. 17L20019.

REFERENCES

B. Tondu, “Modelling of the shoulder complex and

application the design of upper extremities for

humanoid robots”, in Proc. 2005 5th IEEE-RAS Int.

Conf. Humanoid Robots., Tsukuba, Japan, 2006, pp.

313-320.

J. Lenarčič et al, “Positional kinematics of humanoid

arms”, Robotica. vol. 24, no. 1,January, 2006.

J. Yang et al, “Reach envelope of a 9-degree-of-freedom

model,” Int J Rob Autom., vol. 20, no. 4, pp. 240-259,

2005.

K. Kiguchi et al, “Design of a 7DOF upper-limb power-

assist exoskeleton robot with moving shoulder joint

mechanism,” in IEEE Int. Conf. Rob. Biomimetics,

Phuket, Thailand, 2011, pp. 2937-2942.

N. Klopčar and J. Lenarčič, “Bilateral and unilateral

shoulder girdle kinematics during humeral elevation,”

Clin. Biomech. vol. 21, no. supp-S1, pp. 20-26, 2006.

N. Tobias, et al. ARMin III ‒ Arm Therapy Exoskeleton

with an Ergonomic Shoulder Actuation. Appl. Bionics.

Vol. 6 (2009) No. 2, p. 127-142.

R. F. Kirsch et al, “Model-based development of

neuroprostheses for restoring proximal arm function”,

J. Rehabil. Res. Dev, vol. 38, no. 6, pp. 619-626, 2001.

W. Maurel, et al, “Human shoulder modeling including

scapulo-thoracic constraint and joint sinus cones,”

Comput. Graph-uk., vol. 24,no. 2, pp. 203-218, 2000.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

226