Research on Unmanned Vehicle Path Planning based on Improved

Artificial Potential Field Method

Guiling Ju

1, a, *

, Weihai Sun

, Hongjuan Hu

and Yuanyuan Wu

Mathematics of Department of Basic Courses, Academy of Army Armored Forces, Beijing, China

Vehicle Engineering Department, Academy of Army Armored Forces, Beijing, China

English of Department of Basic Courses, Academy of Army Armored Forces, Beijing, China

Keywords: Path planning, artificial potential, unmanned vehicle, simulation experiments.

Abstract: Path planning is one of the most important tasks in unmanned vehicle navigation system. Artificial potential

field method has been widely used in real-time obstacle avoidance trajectory control due to its advantages of

simple structure, less computation and strong robustness. However, it also has the problems of local

minimum point and unreachable target. Aiming at this defect of artificial potential field method in

unmanned vehicle path planning, the gravitational potential field function and repulsive potential field

function were improved, and the effectiveness of the algorithm is verified by simulation experiments.

1 INTRODUCTION

Unmanned vehicle is of great significance in

alleviating road congestion, reducing traffic

accidents and reducing driver fatigue. In the

unmanned vehicle system, path planning is the basis

of intelligent vehicle navigation and control. For the

problem of path planning, many algorithms are

proposed, such as genetic algorithm, ant colony

algorithm, particle swarm optimization, neural

network algorithm and so on. These algorithms play

a positive role in the research of path planning, but

they also have arithmetic. The method is complex

and computationally expensive, and it is inefficient

for path planning (H. Liu, J. Mao 2013; L.Yin, Y. X.

Yin, 2009; D. Q. Shi, E. G. Collins, D. Dunlap,

2008). The artificial potential field method has the

advantages of simple structure, small calculation and

easy control. Therefore, it has been widely used in

real-time obstacle avoidance. However, the

traditional artificial potential field method has the

following shortcomings: 1) no path can be found

between two obstacles close to each other; 2) there is

oscillation problem in front of obstacles; 3) When

there are obstacles near the target point, it can not

reach the target point; 4) there is a local minimum

(C. L. Liu, 2012; J. Y. Zhang, T. Liu, 2007; X. X.

Liang, et.al, 2018; J. Y. Zhang, et.al, 2006).

Aiming at the problem of target unreachability

and local minimum point in the path planning of

unmanned vehicle, this paper studies it.

2 ARTIFICIAL POTENTIAL

FIELD METHOD

Artificial potential field method (C. L. Liu, 2012)

was proposed by Khatib in 1986. The basic idea is to

regard the motion of the unmanned vehicle as a kind

of motion in the virtual artificial force field. The

target point produces gravitation to the unmanned

vehicle, while the obstacle produces repulsion to the

unmanned vehicle. The unmanned vehicle avoids the

obstacle and moves to the target point under the

combined force of gravitation and repulsion.

Note as gravitational potential field

function, the traditional function of it is usually

taken as follows

() (, )

att g

Ux xx





(1)

In the formula, represents the gravitational

potential field coefficient, represents the current

position of the unmanned vehicle, represents the

()

att



Ju, G., Sun, W., Hu, H. and Wu, Y.

Research on Unmanned Vehicle Path Planning based on Improved Artiﬁcial Potential Field Method.

DOI: 10.5220/0008869204310434

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 431-434

ISBN: 978-989-758-412-1

431

position of the target point, and represents

the distance between the position of the unmanned

vehicle and the position of the target point. From

this function, it can be seen that the larger the

distance between the unmanned vehicle and the

target point, the stronger the gravitational potential

field function and the greater the gravitation.

Note as repulsive potential field

function, the traditional function of it is usually

taken as follows:

111

,(,)

()

2(,)

0, ( , )

rep



























(2)

In the formula, represents the repulsive

potential field coefficient, represents the

distance between the current position of the

unmanned vehicle and the position of the obstacle,

and represents the repulsive force acting

distance of the obstacle. From this function, the

smaller the distance between the unmanned vehicle

and the obstacle, the stronger the repulsive potential

field and the greater the repulsion.

Note as the potential field of the position

which the unmanned vehicle locates, it is taken as

follows

() () ()

att rep

Ux U x U x

Note

(), (), ()

att rep

xF xFx

as gravitation,

repulsion and resultant force of the unmanned

vehicle respectively.

() () () () ()

att rep att rep

xFxFx Ux Ux 

The unmanned vehicle moves to the target point

under the resultant force.

3 IMPROVEMENT OF

ARTIFICIAL POTENTIAL

FIELD METHOD

Aiming at the problems of the artificial potential

field method in the path planning of unmanned

vehicle, the algorithm is improved.

3.1 Target Unreachable Problem and

Solution

If there are obstacles near the target point, the

unmanned vehicle moves closer to the target point

and closer to the obstacle at the same time.

According to the definition of the gravitational

potential field and the repulsive potential field

function mentioned above, in the process of moving

to the target point, the gravitation will be smaller

and smaller, while the repulsion will be larger and

larger. When the repulsion is greater than the

gravitation, the unmanned vehicle will not continue

to move towards the target point, which will lead to

the problem of not reaching the target point.

Therefore, the repulsive potential field function is

improved by introducing the power of distance

factor between unmanned vehicle and target point.

(, )

,(,)

()

2(,)

0, ( , )

rep































(3)

Formula (3) shows that the repulsion will be

greatly reduced when the unmanned vehicle moves

towards the target point, and the repulsive potential

field will be the smallest at the target point. Thus, it

is ensured that he local minimum point only toccurs

at point

and the unreachable problem can be

avoided.

3.2 Local Minimum Point Problem and

Solutions

In the process of driving, when the gravitation and

repulsion of the unmanned vehicle are the same and

the direction is opposite, the resultant force of the

unmanned vehicle is 0, and the unmanned vehicle

cannot continue to move forward, thus causing the

local minimum point problem.

In order to avoid this problem, when the

unmanned vehicle enters the local minimum point,

the direction of gravitational potential field can be

changed artificially, so that the force at the point

becomes unbalanced, so as to help the unmanned

vehicle find the next moving point.

The gravitational potential field function is

modified as follows

cos sin

() (, )

sin cos

att g

Ux xx

















(4)

(, )



()

rep



(, )



()Ux

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

432

In the formula (4), the variable



represents the

angle of the change of the gravitational potential

field direction.

Because of the random angle



, the direction of

the oscillating potential field can be selected

randomly to ensure the operation of the oscillating

potential field, so that the unmanned vehicle can

jump out of the current point, and then the path

planning is carried out according to the artificial

potential field method function (1). If the unmanned

vehicle falls into the local minimum state again, the

gravitational potential field function is switched

from function (1) to (4). Then it goes down in turn

until the unmanned vehicle avoids all the local

minimum points in the driving process and reaches

the target point.

4 SIMULATION VERIFICATION

In order to verify the effectiveness of the improved

artificial potential field method, the simulation

experiment is carried out through software

MATLAB. For the convenience of discussion, the

size and shape of unmanned vehicles and obstacles

are treated as a particle.

In the simulation, the starting point is (0, 0), (9.7,

9.7) is the target point. Obstacles are represented by

small circles, target points are represented by

triangles, the gain coefficients of gravitation and

repulsion are 5 and 1 respectively, and the deviation

angle is 30 degrees. The results of path planning are

shown in the figure.

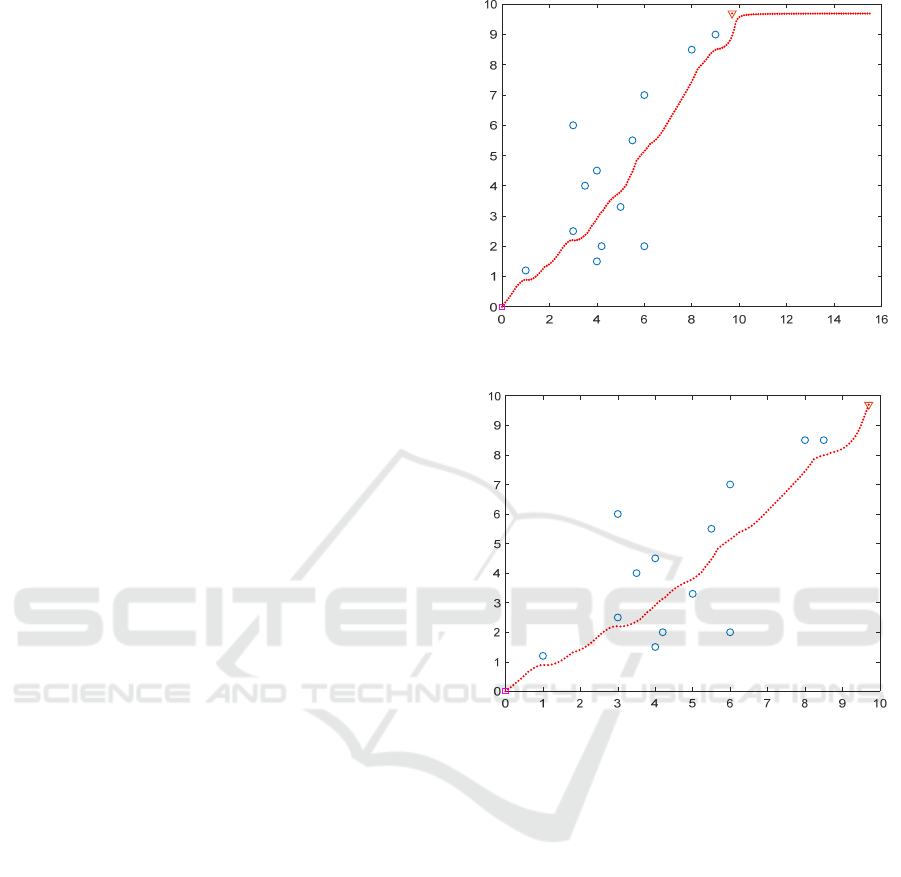
Aiming at the obstacles near the target point and

the repulsion is greater than gravitation, the path

planning curves of the traditional artificial potential

field method and the improved artificial potential

field method are given in Fig.1 and Fig.2

respectively. The simulation results show that the

improved artificial potential field method can

effectively avoid the problem that the unmanned

vehicle cannot reach the target point.

Figure 1. Traditional artificial potential field method.

Figure 2. Improvement of artificial potential field method.

Aiming at the problem of local minimum, the

path planning curves of traditional artificial potential

field method and improved artificial potential field

method are given in Fig.3 and Fig.4. The simulation

results show that the improved artificial potential

field method can effectively avoid the problem of

local minimum.

Research on Unmanned Vehicle Path Planning based on Improved Artiﬁcial Potential Field Method

433

Figure 3. Traditional artificial potential field method.

Figure 4. Improvement of artificial potential field method.

5 CONCLUSION

The artificial potential field method may cause local

minimum and unreachable problems in path

planning. To solve this problem, the gravitational

potential field function and repulsive potential field

function are improved. The feasibility of this method

is verified by simulation. However, it does not

consider whether the planned path is the optimal

path and whether the planned path is smooth, etc.

These problems need further study.

ACKNOWLEDGMENTS

This work was financially supported by the college's

self-initiated fund project 2018CJ31.

REFERENCES

C. L. Liu, Research on robot path planning technology

based on potential field method and genetic

algorithms, Nanjjing. Uni.Tech.,Nanjing, 2012, pp.

651–654.

D. Q. Shi, E. G. Collins, D. Dunlap, Robot navigation in

cluttered 3-D environments using preference-based

fuzzy behaviors, Sys, Man and Cybernetics, Commun.

7(2008)1486-1499.

H. Liu, J. Mao, Walking stability simulation of excavators

under complex road conditions, J. Liaoning. Tech.

Uni., Commun. 32 (2013) 377-380.

J. Y. Zhang, T. Liu, Optimal path planning for mobile

robots based on artificial potential field method, J.

Aeronautics, Commun. 28(2007) 183-188.

J. Y. Zhang,Z. P. Zhao, T. Liu, Robot path planning based

on artificial potential field method, J. Harbin

University of Technology, Commun. 38(2006) 1306-

1309.

L.Yin, Y. X. Yin, Path planning simulation based on

dynamic artificial potential field method, J.

Sys.Simulation, Commun. 21(2009) 3325-3341.

X. X. Liang, C. Y. Liu, X. L. Song, Y. K. Zhang, Path

planning of mobile robot based on improved artificial

potential field method, Computer simulation,

Commun. 35(2018) 291-295.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

434