
Research on Charging Strategy Optimization of Electric Vehicle
based on AGA
Bowen Xu
1, a
1
Chongqing University of Posts and Telecommunications, China
Keywords: AGA; intelligent charging; electric vehicle; charging strategy.
Abstract: Because the charging load of electric vehicles is random in time and space, a large number of disorderly
charging of electric vehicles will lead to the peak load of distribution network exceeding the limit of
equipment, which will bring adverse effects on the operation of power grid. In order to smooth the daily
load curve of distribution network, this paper establishes a solution model of intelligent charging control
strategy for large-scale electric vehicle considering the charging demand constraints of electric vehicle
users, and uses adaptive genetic algorithm (AGA) to solve the model. Taking IEEE33 bus distribution
network as an example, based on Monte Carlo stochastic simulation of large-scale electric vehicle grid-
connected scene, the impact of electric vehicle load on distribution network under two control modes of
disorderly charging and intelligent charging is studied comparatively, and the effectiveness of this method is
verified.
1 INTRODUCTION
Global climate and environmental issues have
prompted countries around the world to develop and
utilize renewable energy on a large scale as a
strategy for energy security. The development of
electric vehicles (EVs) is of dual importance in
promoting the efficient use of renewable energy and
reducing fossil fuel consumption, which has
attracted wide attention (
ZHANG Wen-liang, WU
Bin, LI Wu-feng, et al., 2009
).
If large-scale electric vehicles are randomly and
disorderly connected to the grid to charge, it will
have a significant impact on the scheduling,
planning, control and protection of the entire power
system. On the time scale, random charging may
lead to peak load "bee-on-bee" phenomenon, which
exceeds the power supply capacity and affordability
of the existing distribution network, thus causing a
series of problems such as voltage overshoot, branch
overload and so on. On the spatial scale, disorderly
decentralized access may lead to three-phase
unbalance of distribution network, damage the
power quality of the network and increase the power
loss and other adverse effects (MA Ling-ling,
YANG Jun, FU Cong, et al, 2013; GAO Ci-wei,
ZHANG Liang, 2011; KRISTIEN CN, EDWIN H,
JOHAN D, 2010). Therefore, the research on
charging control strategy aiming at reducing the
impact of large-scale electric vehicle access on
distribution network has become a hot issue.
Documents (SUN Xiao-ming, WANG Wei, SU
Su, et al, 2013; GE Shao-yun, HUANG Liu, LIU
Hong, 2012) put forward the method of transferring
charging power of EV to daily load trough through
the guidance of time-sharing tariff policy. But when
large-scale EV is centralized connected to grid or
unreasonable design of valley tariff period may lead
to new load peaks and new problems. Literature
(LUO Zhuo-wei, HU Ze-chun, SONG Yong-hua, et
al, 2012) studied the charging control strategy of EV
under the mode of switching power, aiming at
minimizing the total charging cost and minimizing
the fluctuation of the total load curve. However,
based on a large number of assumptions, this paper
lacks certain practicability. Literature (ERIC S,
MOHAMMAD M H, JAMES MAC PHERSON S
D, et al, 2011) proposes three different objective
functions: minimum load variance, maximum load
factor and minimum network loss, and compares the
optimization results and calculation time of the three
models. However, it investigates the total load
power of load nodes and does not involve making
appropriate charging plans for each electric vehicle.
Literature (WANG Xiu-yum, REN Zhi-qiang, CHU
Xu, B.
Research on Charging Strategy Optimization of Electric Vehicle based on AGA.
DOI: 10.5220/0008870302270234
In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 227-234
ISBN: 978-989-758-412-1
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
227

Dong-qing, 2008) establishes a charging
optimization model for EV with the objective of
minimizing the loss of distribution network, and
considers the user's charging demand and voltage
amplitude constraints. Literature (TIAN Wen-qi, HE
Jing-han, JIANG Jiu-chun, et al, 2013) studies the
multi-objective optimization problem aiming at the
uniform distribution of charging load, the minimum
charging time and the minimum distance of electric
vehicles, and compares the computational
characteristics of particle swarm optimization (PSO)
and genetic algorithm (GA).
This paper takes the conventional charging mode
of electric private car as the research object,
combines the space-time characteristics and
charging characteristics of large-scale electric
vehicle, considers the user's charging demand and
the constraints of safe and stable operation of the
power grid, and takes the minimum standard
deviation of the total load curve of the power grid as
the control objective, establishes the intelligent
charging strategy of large-scale electric vehicle. The
mathematical model is solved slightly, and an
adaptive genetic algorithm is proposed to optimize
the charging plan. Based on the proposed model and
method, taking IEEE33 bus distribution system as an
example, the effects of intelligent charging and
disordered charging on distribution network are
studied.
2 INFLUENCING FACTORS OF
CHARGING LOAD OF LARGE-
SCALE ELECTRIC VEHICLE
There are many factors affecting the charging load
of large-scale electric vehicles, which can be
summarized as the scale of electric vehicles, battery
characteristics, charging mode, user behavior,
charging strategy, etc. (YANG Bing, WANG Li-
fang, LIAO Cheng-lin, 2013). The battery capacity
of electric vehicle determines the maximum mileage
and charging frequency of the vehicle. The larger the
battery capacity, the farther the vehicle travels, the
lower the charging frequency correspondingly.
However, the battery capacity of different models is
different. Generally speaking, the battery capacity
requirement of electric bus is much larger than that
of electric private car.
At present, there are three charging modes:
conventional charging, fast charging and battery
replacement. Conventional charging is to charge
batteries slowly in a relatively low charging current
for a longer period of time. Generally, the charging
time is 8-l0h. This mode is mainly aimed at a large
number of low-voltage (220V) distributed charging
points (mainly concentrated in residential buildings
and office parking lots). Its advantages are low cost,
small size and practicability of charging facilities.
On-board now. Fast charging mode is a charging
method that makes the battery reach or close to full
state in a short time. Its typical charging time is 10-
30 minutes. This mode can quickly solve the
problem of power supply when the endurance
mileage is insufficient, but it requires a higher power
grid and is only suitable for large charging stations.
Battery replacement is achieved by directly
replacing the battery pack of electric vehicles to
achieve the purpose of charging. The whole battery
replacement process can be completed in 10
minutes. For the batteries replaced, the conventional
charging method is generally used for centralized
charging. This mode does not need on-site charging,
so it can be arranged in the low load period, which is
conducive to reducing the peak-valley difference of
the power grid. It also effectively solves the
problems of short endurance mileage of general
batteries, and is conducive to the maintenance and
recovery of batteries. But this mode needs to build
large-scale centralized charging station, special
power grid, and uniform shape and parameters of
batteries.
The user behavior that affects the electric power
demand of EV mainly includes the starting charging
time, starting power and expected power of EV. The
more concentrated the initial charging time of users,
the more prominent the power demand of large-scale
electric vehicles, and the greater the impact on the
power grid. The initial charge reflects the user's
power consumption, while the expected charge
determines the charging duration at a certain
charging power. Referring to reference (SOARES F
J, 2016), this paper studies the travel law of EV
based on Markov chain, so as to determine the
charging time and the end time of EV.
Similarly, the demand for electric power varies
with different charging strategies. At present,
charging strategies are mainly divided into three
categories: disordered charging, time-sharing pricing
policy and intelligent charging. Unordered charging
usually starts after the last trip or when the battery
power is below a certain threshold. It can be
imagined that large-scale disordered charging will
bring many adverse effects to the power grid. Time-
of-use tariff policy is a common market regulation
mechanism, which means that in the low load
period, users can be guided to charge in the low load
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
228

period by lowering the tariff, thus playing a certain
role in filling the valley. Intelligent charging refers
to the optimal operation of the power grid by
reasonably arranging the charging plan of electric
vehicles.
3 MATHEMATICAL MODEL
FOR OPTIMIZING
INTELLIGENT CHARGING OF
ELECTRIC VEHICLES
3.1 Objective Function
This paper studies the charging schedule of electric
vehicles in one day, and divides the day into T
periods. Taking the charging of No. i electric vehicle
at time t as the independent variable and the
minimum standard deviation of the total load as the
control objective, i.e.
(1)
Formula: N is the total number of electric
vehicles; T is the total calculation time;
is the
"1/0" independent variable to represent the electric
vehicle i charging or not at t times;
is the
electric vehicle i the rated charging power, unit kW;
is the charging efficiency;
is the total
amount of conventional load in the network at t
times, unit kW;
represents the average value of
the daily load curve. The specific calculation
formula of
is as follows:
(2)
3.2 Constraints
(1) Customer Charging Demand Constraints
In order to meet the user's needs when leaving,
constraints need to be met:
(3)
(4)
Formula: SO
represents i the starting power of
an electric vehicle; ∆represents the calculation time
step;
represents the rated battery capacity of an
electric vehicle of i. The formula constrains the
charging time, which means that the electric
vehicle's power consumption reaches the user's
expectation at least when the user leaves.
The recursive formulas of electric quantity at
each time are given:
(5)
In the formula, SO
represents the power
consumption of an electric vehicle at time t+1.
Obviously, if
= 0, SO
SO
, which means
that if the electric vehicle is not charged at the
current moment, the vehicle power will not change
at the next moment.
(2) Uncontrollable time constraints
(6)
Where, 6 is the time when the electric vehicle is
connected to the grid. This paper assumes that the
user will be merged into the grid at the end of the
last trip; Ukraine is the time when the electric
vehicle leaves. This formula indicates that only
when the electric vehicle is connected to the grid can
it be charged.
(3) Node Voltage Constraints
(7)
Where,
and
represent the upper and
lower voltage constraints of node j, respectively.
4 ADAPTIVE GENETIC
ALGORITHM
Genetic algorithm (GA) is a kind of randomized
search method based on the evolutionary law of the
biological world. Through a series of operations
such as selection, crossover and mutation, the
individuals with the greatest fitness obtained in the
evolutionary process are taken as the output of the
optimal solution. However, simple genetic algorithm
uses fixed crossover probability and mutation
probability, ignoring the adaptive characteristics in
the process of population evolution, which will
affect the global search ability and premature
Research on Charging Strategy Optimization of Electric Vehicle based on AGA
229
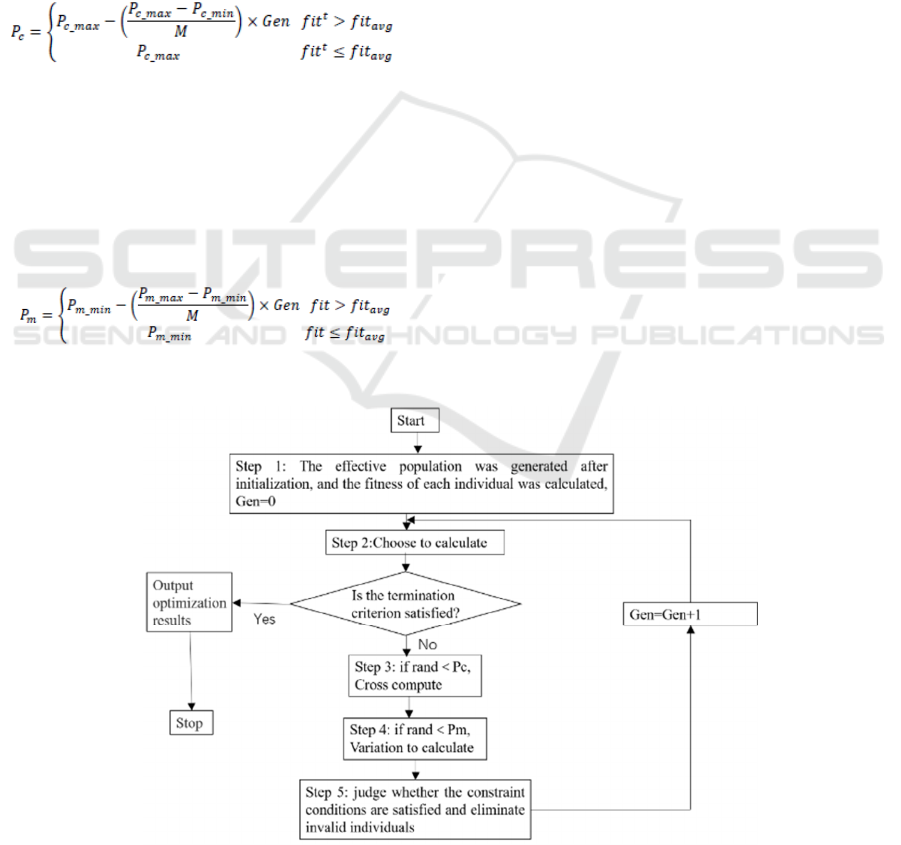
convergence into local optimum. The adaptive
genetic algorithm (AGA) uses the dynamic
generation method to determine the adaptive
crossover and mutation probability, so as to maintain
the genetic diversity of individuals and prevent the
genetic algorithm from premature convergence to
local optimum. By comparing AGA with GA in
dealing with some optimization problems, it is found
that AGA can quickly converge to the global
optimum. Therefore, this paper adopts adaptive
genetic algorithm to study the intelligent charging
strategy of electric vehicles.
Adaptive crossover probability Pc and mutation
probability Pm can be obtained by the following
formula:
(8)
In the formula,
_
is the maximum crossover
probability;
_
is the minimum crossover
probability; Gen is the current iteration number: M
is the maximum number of iterations;
is the
larger fitness in a crossover operation;
is the
average fitness of all individuals in the current
iteration.
(9)
In the formula:
_
is the maximum mutation
probability;
_
is the minimum mutation
probability; Gen is the current iteration number; M
is the maximum iteration number; fit represents the
fitness of the individual in the current mutation
operation. Fig. 1 is the flow chart of the adaptive
genetic algorithm.
Before the operation starts, the environment
variables of the adaptive genetic algorithm need to
be set, such as the maximum number of iterations M,
population size N, intersection and variation
parameters Pc_max, Pc_min, Pm_max, Pc_min, The
specific operation steps are as follows:
The first step is to initialize, generate effective
population, and calculate the fitness of each
individual;
The second step is to select and retain N
individuals with better fitness. If the optimal fitness
satisfies the set goal or reaches the maximum
number of iterations, the optimal result is output and
the operation is stopped, otherwise the next step will
be taken.
The third step is crossover operation. When the
random variable is less than the adaptive crossover
probability, the single point crossover of parents and
children is performed. Thus, 2N offspring
individuals are generated from N parents, and the
parents and offspring are combined to form a new
population.
The fourth step is mutation operation. For new
populations, mutation occurs when the random
variable is less than the adaptive mutation
probability.
Fig 1. Operation flow chart of the adaptive genetic algorithm.
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
230
Fifth step: Constraint judgment is made on 3N
individuals, invalid individuals are eliminated, and
N individuals with better fitness are retained, then
the second step is returned, and the number of
iterations is increased once.
To study the intelligent charging problem of
large-scale electric vehicles, this paper adopts
adaptive genetic algorithm with binary coding, uses
independent variable
to represent the charging
state of ist electric vehicle at t-time,
1 to
indicate charging:
= 0 to indicate not charging.
5 ANALYSIS OF EXAMPLES
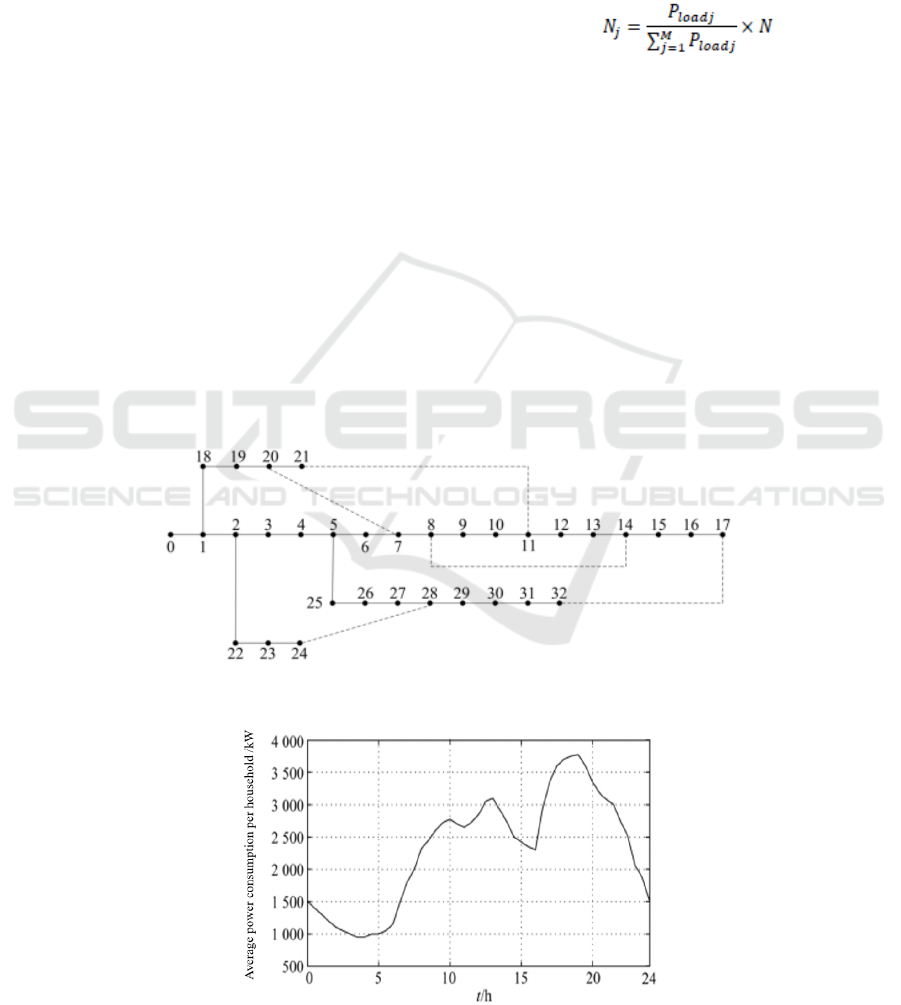
Taking IEEE33 bus residential distribution network
as an example, as shown in Figure 2, the impact of
charging load on distribution network of large-scale
electric vehicles under two charging strategies of
disorderly charging and intelligent charging is
studied. The routine daily load curve of the example
system is shown in Figure 3 (KRISTIEN C, EDWIN
H, JOHAN D, 2010).
Assuming that there are 600 electric vehicles in
this area, the user chooses to merge them into the
grid after the last trip, so the starting charging time
of each electric vehicle is t0. The departure time td
can be simulated by Markov chain.
Considering the actual situation, all electric
vehicle loads are allocated to different nodes in
geographic space according to the proportion of the
conventional load of each node to the total load for
charging (GARCIA-VALLE R, LOPES J A P,
2013), which is shown in the following formula:
(10)
In the formula:
is the number of electric
vehicles allocated by node j; N is the total number of
electric vehicles;
is the normal load size of
node j connection;
∑
is the total amount of
normal load in distribution network; M is the
number of nodes in network.
In order to simplify the analysis, it is assumed
that the rated battery capacity of each electric
vehicle is Ci=60kWh; the rated charging power is
PEvi=4kW; the charging efficiency is η=95%; and
the initial power is SO
. It obeys truncated Gauss
distribution, with a mean of 40, a variance of 20, a
minimum SO
20 and a maximum SO
50; the
user's expected charge capacity obeys the uniform
distribution between (80, 100).
Fig 2. IEEE 33-nodes distribution system.
Fig 3. Daily load profile of the test system.
Research on Charging Strategy Optimization of Electric Vehicle based on AGA
231
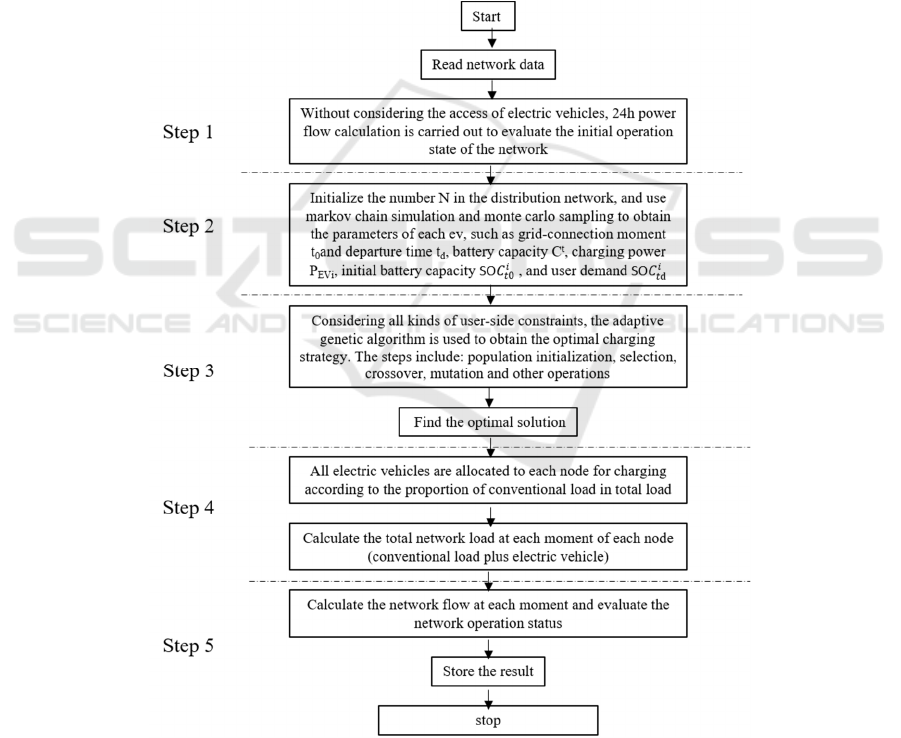
In this paper, the specific parameters of the
adaptive genetic algorithm are set as follows: the
number of genetic iterations is 80, the total number
of individuals in the population is 200, the maximum
crossover probability Pc_max = 0.9, the minimum
crossover probability Pc_min = 0.4, the maximum
mutation probability Pm_max = 0.1, and the
minimum mutation probability Pm_max = 0.01. The
specific operation flow is shown in Figure 4.
The intelligent optimal charging strategy
proposed in this paper is compared with disordered
charging, and the results are shown in Fig. 5.
The peak-valley difference rate in Table 1 is the
ratio of peak-valley difference to peak load. From
Fig. 5 and Table 1, it can be seen that under the
disordered charging strategy, users access the power
grid after the last trip and start charging
immediately. Therefore, in the evening, the overlap
between the electric vehicle load and the original
load presents a "peak" phenomenon, which increases
the peak-valley difference of the system, and
reduces the utilization rate of power resources, and
will have a negative impact on the power grid.
Under the intelligent charging strategy, the charging
load of most electric vehicles is transferred to the
low valley period of the original load. Compared
with the disordered charging, it can reduce the peak-
valley difference and make the total load curve more
flat, which is conducive to reducing the number of
unit start-up and shutdown, and improving the
security and economy of the system operation.
Fig 4. Flow chart intelligent algorithm.
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
232
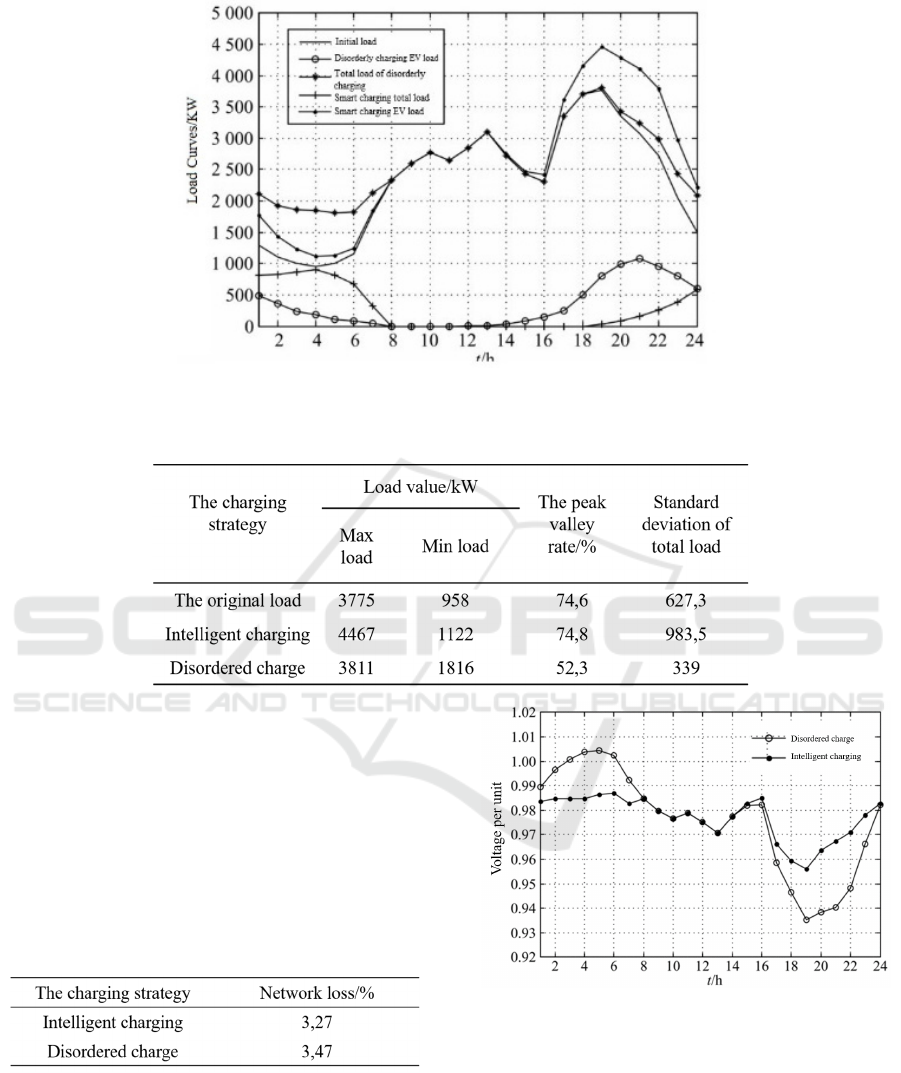
Fig 5. Load curves under two control strategies.
Table 1. Comparisons of system load level indexes.
In this model, the voltage offset of node 17 is the
largest, which can reflect the impact of electric
vehicle access on the node voltage, and is
representative. Therefore, this point is taken as the
research object to study the voltage offset of the
node. Figure 6 shows the voltage offset at each time
of node 17. As can be seen from the figure,
intelligent charging can effectively reduce voltage
offset.
Table 2. Comparisons of system losses.
As can be seen from Table 2, the network loss of
intelligent charging is less than that of disorderly
charging, because when the total load is fixed in a
day, The flatter the daily load curve, the smaller the
loss; conversely, the greater the difference between
peak and valley, the greater the loss.
Fig 6. Comparisons of voltage deviation of bus 17.
Figure 7 shows the convergence curve of the
optimization algorithm. When the iteration is about
60 times, the optimal solution is obtained, which
proves that the optimization algorithm has good
convergence.
Research on Charging Strategy Optimization of Electric Vehicle based on AGA
233

Fig 7. Convergence of the optimization algorithm.
6 SUMMARY
This paper presents a solution model and method of
intelligent charging control strategy for large-scale
electric vehicles. The key of this model is to
consider the user's charging demand and grid side
constraints, and to minimize the standard deviation
of total load as the optimization objective. An
example is given to study the intelligent charging
with each charging plan as the control variable. The
effectiveness of the proposed model and method is
verified by comparing the effect of the disorderly
charging mode on the load of the electric vehicle.
Based on this model and method, other types of
objective functions can also be considered, such as
maximum absorption of renewable energy
generation, and so on. In addition, based on Monte
Carlo scenario random simulation and distribution
network power flow calculation, the model can also
be used to evaluate the impact of a given scale of
electric vehicle access on distribution network and
the maximum penetration level of electric vehicles
in distribution network.
REFERENCES
ERIC S, MOHAMMAD M H, JAMES MAC PHERSON
S D, et al. Coordinated charging of plug-in hybrid
electric vehicles to minimize distribution system
losses [J]. IEEE Trans on Smart Grid, 2011, 2(1): 198-
205.
GAO Ci-wei, ZHANG Liang.A survey of influence of
electrics vehicle charging on power grid [J]. Power
System Technology, 2011, 35(2):127-131.
GARCIA-VALLE R, LOPES J A P. Electric vehicle
integration into modern power networks [M]. Berlin:
Springer, 2013.
GE Shao-yun, HUANG Liu, LIU Hong. Optimization of
peak-valley TOU power price time-period in ordered
charging mode of electric vehicle [J]. Power system
Protection and Control, 2012, 40 (10):1-5.
KRISTIEN C, EDWIN H, JOHAN D. The impact of
charging plug-in hybrid electric vehicles on a
residential distribution grid [J]. IEEE Trans on Power
Systems, 2010, 25(1):371-380.
KRISTIEN CN, EDWIN H, JOHAN D. The impact of
charging plug-in hybrid electric vehicles on a
residential distribution grid [J]. IEEE Trans on Power
Systems, 2010, 25(1):371-380.
LUO Zhuo-wei, HU Ze-chun, SONG Yong-hua, et al.
Study on charging load modeling and coordinated
charging of electric vehicles under battery swapping
modes [J]. Proceedings of the CSEE, 2012, 32 (31): 1-
10, 212.
MA Ling-ling, YANG Jun, FU Cong, et al. Review on
impact of electric car charging and discharging on
power grid [J]. Power System Protection and Control,
2013, 41(3):140-148.
SOARES F J.A stochastic model to simulate electric
vehicles motion and quantify the energy required from
the grid[C]//Power Systems Computation Conference.
SUN Xiao-ming, WANG Wei, SU Su, et al. Coordinated
charging strategy for electric vehicles based on time-
of-use price [J]. Automation of Electric Power
Systems, 2013, 37(1):191-195.
TIAN Wen-qi, HE Jing-han, JIANG Jiu-chun, et al.
Electric vehicle charging load spatial allocation
optimization algorithm[J]. Transactions of China
Electrotechnical Sosiety, 2013, 28 (3):269-276.
WANG Xiu-yum, REN Zhi-qiang, CHU Dong-qing.
Study of algorithm on distribution network optimum
reconfiguration for reducing line loss[J] Power System
Protection and Control,2008,36(12):21-24.
YANG Bing, WANG Li-fang, LIAO Cheng-lin. Research
on power charging demand of large-scale electric
vehicles and its impacting factors [J]. Transactions of
China Electrotechnical Sosiety, 2013, 28 (2):22-27.
ZHANG Wen-liang, WU Bin, LI Wu-feng, et al.
Discussion on development trend of battery electric
vehicles in China and its energy supply mode [J].
Power System Technology, 2009, 33(4): 1-5.
ZHANG Xue-qing, LIANG Jun, ZHANG Li, et al.
Approach for plug-in electric vehicles charging
scheduling considering wind and photovoltaic power
in Chinese regional power grids[J]. Transactions of
China Electrotechnical Sosiety, 2013, 28 (2): 28-35.
ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering
234
