Investigation of Selection Mechanism of Friction Models in

Multibody Systems

Qian Jing

1, a

, Ning Mi

School of Mechanical Engineering, Long dong University, Qing Yang 745000, China

Keywords: Friction model, Multibody system, Joints; Dynamics, Adams.

Abstract: In order to research the influence of the different friction models on the frictional characteristics and the

dynamic response of the multibody system with different kinds of joints, eleven different kinds of friction

models were used in three different specified scenarios. Firstly, each friction model is simply introduced,

and its friction characteristics are illustrated. In addition, in order to test the physical properties of these

friction models, there are two different scenarios: (i) multibody system with revolute joint; (ii) multibody

system with revolute joint and prismatic joint simultaneously. Secondly, when these friction models are

applied in the scenarios, the comparison analysis between with friction phenomenon model and without

friction phenomenon model is implemented, which is validated by the commercial software ADAMS.

Finally, the simulation shows that the type of joint in the multibody system has a significant effect on the

selection mechanism of these friction models. Namely, this investigation provides a reference method for

choosing the friction model that is the best suitable for the above two different scenarios according to the

computational efficiency and position stability.

1 INTRODUCTION

Friction model is a set of mathematical model used

to calculate the friction and to explain the

mechanism of friction in motion. In general, in order

to use differential equations to describe friction

phenomena, the friction model can be divided into

two types, namely, static friction model and dynamic

friction model (Awrejcewicz Jan, Fečkan Michal,

Olejnik Pawel, 2005), and the basis of improvement

for the static friction model is the Coulomb friction

model (Coulomb P.C.A). The Coulomb model states

that the direction of friction is opposite to the

relative velocity on the contact areas. The magnitude

of the friction is independent of the magnitude of the

relative velocity, but it is proportional to the

magnitude of the normal load. The Coulomb friction

model can be regarded as a description of

macroscopic friction phenomenon, this is mainly

because the effect of dynamic friction is only

considered in relative motion. Hence, the Coulomb

friction model implied a lot of microscopic

phenomena of friction such as a static friction,

Stribeck friction, pre-slip, and viscous sliding are not

considered. Therefore, when the relative velocity

approaches zero, the discontinuity of the friction will

inevitably lead to discontinuity in the solution of

dynamics in the multibody system, which lead to the

result divergent and inaccurate(Armstrong-Hélouvry

B., Canudas Dewit, C, 1995). In fact, the change of

friction in motion must be a continuous process. It

has been proved by a lot of experiments that the

magnitude of friction is closely related to the

magnitude of velocity when the velocity approaches

zero (F. S., A X, Cieszka, et al, 2010). When the

relative velocity approaches zero, the reference (F.

S., A X, Cieszka, et al, 1990; Berger Ej, 2002) based

on a number of experiments pointed out that the

magnitude of friction is simultaneously related to the

static friction coefficient and the dynamic friction

coefficient. If the external tangential force is less

than the static friction, the motion is viscous, and if

the external tangential force is greater than the static

friction force, the motion is sliding. ‘Stribeck effect’

is a micro-description of the excessive states

between viscous and sliding, and it is a great

improvement for the Column model in describing

the frictional mechanism. The degree of agreement

with the experimental data of the friction model can

be greatly improved based on the accurate

description in viscous and sliding. The discontinuous

piecewise function in the Coulomb friction model

Jing, Q. and Mi, N.

Investigation of Selection Mechanism of Friction Models in Multibody Systems.

DOI: 10.5220/0008873602510260

In Proceedings of 5th International Conference on Vehicle, Mechanical and Electrical Engineering (ICVMEE 2019), pages 251-260

ISBN: 978-989-758-412-1

251

can be originally turned into a continuous function,

consequently, the stability of the integrating

processes can be increased. Meanwhile, the

description of ‘ Stribeck effect’ also enhance the

computational accuracy of the dynamics in

multibody systems. How to describe the transition of

viscous and sliding more accurately and solve the

problem of self-excited oscillation and bifurcation

caused by them has become a hot topic in academic

research (Awrejcewicz J, 1998).

In order to solve the problem of the discontinuity

of friction in the Coulomb friction model, the

method of replacing the change curve of the friction

with a specific function has been used in the static

friction model at first when the relative velocity

approached zero (Duan Chengwu, Singh Rajendra,

2006). According to the problem of switching state

equation in friction model, Karnopp put forward the

Karnopp model which create a zero field in a region

of relatively low speed (Karnopp D, 1985). On this

basis, Leine et al (Leine R. I., Campen D. H. Van,

Kraker A. De, et al, 1998) improved the accuracy of

numerical calculation and increased the stability of

the integral process by introducing the definition of

acceleration. Threlfall (Threlfall D. C, 1978)

reduced the discontinuity of friction by using a

system of equations on the basis of the Coulomb

model. Filipe Marques et al (Marques Filipe, Flores

Paulo, Pimenta Claro J. C., et al, 2016) improved the

Threlfall model at the aspect of coefficient’s

improvement and made friction closer to the result

of the Coulomb model when the relative velocity

approaches zero. In order to obtain the ‘Stribeck

effect’, Bengisu and Akay (Bengisu M. T., Akay A,

1994) used two algebraic equations, one of them

describes the sliding and another especially

describes the ‘Stribeck effect’. Awrejcewicz

(Awrejcewicz J, Grzelczyk D, Pyryev Yu, 2009)

refined the stick-slip process and proposed a novel

friction model which is expressed as four equations.

The friction model mentioned above are some static

friction model used in high frequency in the

dynamic calculation of multibody systems in recent

years. In addition, there are many other static

friction models, for example, the Wojewoda et al

model (Wojewoda J, Stefański A, Wiercigroch M, et

al, 2008), the Ambrósio model (Ambrósio Jorge A.C,

2003), the Benson model (Benson David J.,

Hallquist John O, 1990) used in Multi-body system

software COMSOL and the Velocity-based model

used in dynamic simulation software ADAMS and

so on. Dahl firstly put forward the Dahl model (Dahl

P. R, 1968) based on microscopic deformation of

bristle, the relative motion regarded as a deformation

similar to the spring between contact surfaces in the

static stage of the friction was considered for the

first time. Based on the assumption of bristle

deformation, there are still many other models which

also think about the static friction, for instance, the

LuGre model (De Wit C. Canudas, Olsson H,

Astrom K. J, et al, 1995), the Elasto-plastic model

(Dupont P., Armstrong B., Hayward V, 2002), the

Stick-slip model (Cha Ho Young, Choi Juhwan, Han

Sik Ryu, et al, 2011) and the Gonthier model

(Gonthier Yves, Mcphee John, Lange Christian, et al,

2004) and so on. Compared to static friction models,

the most of the dynamic friction models can more

clearly and effectively reflect the friction

characteristics in the movement of the multibody

systems, thus, the more accurate results of the

dynamic analysis can be obtained. However, the

dynamic friction model contains state variables and

involves many parameters. How to determine the

value of each parameter and choose a more effective

step and method of the iteration is very important to

solve the problem as the friction phenomena are

considered in the process of motion in multibody

systems.

The purpose of this study is to analyze the effects

of different friction models on the characteristics in

friction and the results of kinematics analysis in

multibody systems with different kinds of joints.

There are eleven common friction models were

selected as research objects in this paper, in which

the static friction models respectively are the

Smooth Coulomb model, the Threlfall model, the

Bengisu model, the Karnopp model, the Velocity-

based model and the Awrejcewicz model, and the

dynamic friction models respectively are the Dahl

model, the LuGre model, the Elasto-plastic model,

the Stick-slip model and the Gonthier model. Two

typical mechanisms which only contain prismatic

joints and simultaneously contain prismatic joints

and revolute joints respectively are tested, and the

result of dynamics is compared with Adams. The

influence of friction models on the results of

kinematic simulation for different types of

multibody systems is illustrated based on the

computational efficiency and the stability of the

numerical solution of the position. Finally, the

optimal selection method of eleven friction models

for different types of multibody systems is obtained,

which provides a reference for how to more

accurately and effectively solve the dynamic

analysis when the characteristics in friction need to

be considered in the future.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

252

2 STRUCTURE OF THE

INVESTIGATION

This paper is aimed to present and compare several

friction models that can be used in multibody

systems containing different kinds of joints. In order

to obtain the frictional characteristics at low-

speed motion and the accurate solution of the

dynamics in a multibody system, two aspects of

research are mainly done in this paper. In section 3

and section 4, six kinds of static and five kinds of

dynamic friction models commonly used in a lot of

previous literature were concluded respectively and

their algebraic equations were briefly introduced.

The comparison of the ability for describing the four

kinds of friction phenomena is previewed in section

5. In section 6, three types of mechanical systems

that only include prismatic joints, only include

revolute joints and simultaneously include prismatic

joints and revolute joints are selected as the research

objects. In section 7, the influence of the different

friction models on the friction characteristics and

computational dynamics in multibody systems with

different kinds of joints is analyzed according to the

computational efficiency and the stability of

simulation results, and a reference method is

provided for choosing the friction model that is the

best suitable for three different scenarios mentioned

in the preceding section in the end.

3 COMPARISON BETWEEN

FRICTION MODELS

This study takes into account the number of design

parameters, the difficulty of parameter selection and

the calculation efficiency of the friction model. Six

static friction models and five dynamic friction

models are selected for a brief introduction, and the

mathematical equations of friction are listed. The

ability of the description of friction phenomena is a

very important evidence in estimating the

computational accuracy of the friction (Gonthier

Yves, Mcphee John, Lange Christian, et al, 2004),

and the expression of friction model need to be

consistent with actual conditions, which depends on

the number of friction phenomena that can be

accurately described. However, it is impossible to

take all of the influence factors of friction into

account. This paper focuses on four kinds of friction

phenomena, namely, the dynamic friction, the static

friction, the "Stribeck effect" and the pre-sliding,

See Table 1 for contrastive details.

Table 1. Phenomena of friction models.

Name

Dynamic

Friction

Static

Friction

Stribeck

Pre-

sliding

Smooth

Threlfall

Bengisu

Karnopp

Velocity-

based

Awrejcewicz

Dahl

LuGre

Elasto-

plastic

Stick-slip

Gonthier

Where means it can be described, means it

can’t be described. It can be seen from Table 2 that

the dynamic friction model compared with the static

friction model generally reflects the pre-sliding due

to the consideration of the average deformation of

the bristle in the static friction. In addition, when the

four kinds of friction phenomena mentioned above

can be all observed it is necessary to investigate

other friction phenomena for the actual requirement

and select an appropriate friction model according to

the efficiency of calculation and the complexity of

parameters used in the friction model.

4 NUMERICAL EXAMPLES AND

COMPARISON

The advantages and drawbacks of the proposed

friction model have briefly introduced above, and

the specific calculation process is summarized. The

purpose of this study is to analyze the influence of

different friction models on the frictional

characteristics and the results of the kinematic

analysis in the multibody systems with the different

kinds of joints in the case of dry friction. The

mechanisms are the Rabinowicz case, the single

pendulum, and the single pendulum box respectively.

The dynamic simulation of them is carried out and

the results of the analysis are compared with

ADAMS.

4.1 Model with Prismatic Joints

The Rabinowitz case composed of sliders and

springs is a single degree of freedom (DOF) model,

and it is often used to study the viscous and sliding

of friction phenomena in the dynamic test of

multibody systems. After a lot of research and

continuous improvement (Marques Filipe, Flores

Investigation of Selection Mechanism of Friction Models in Multibody Systems

253

Paulo, Pimenta Claro J. C., et al, 2016), the

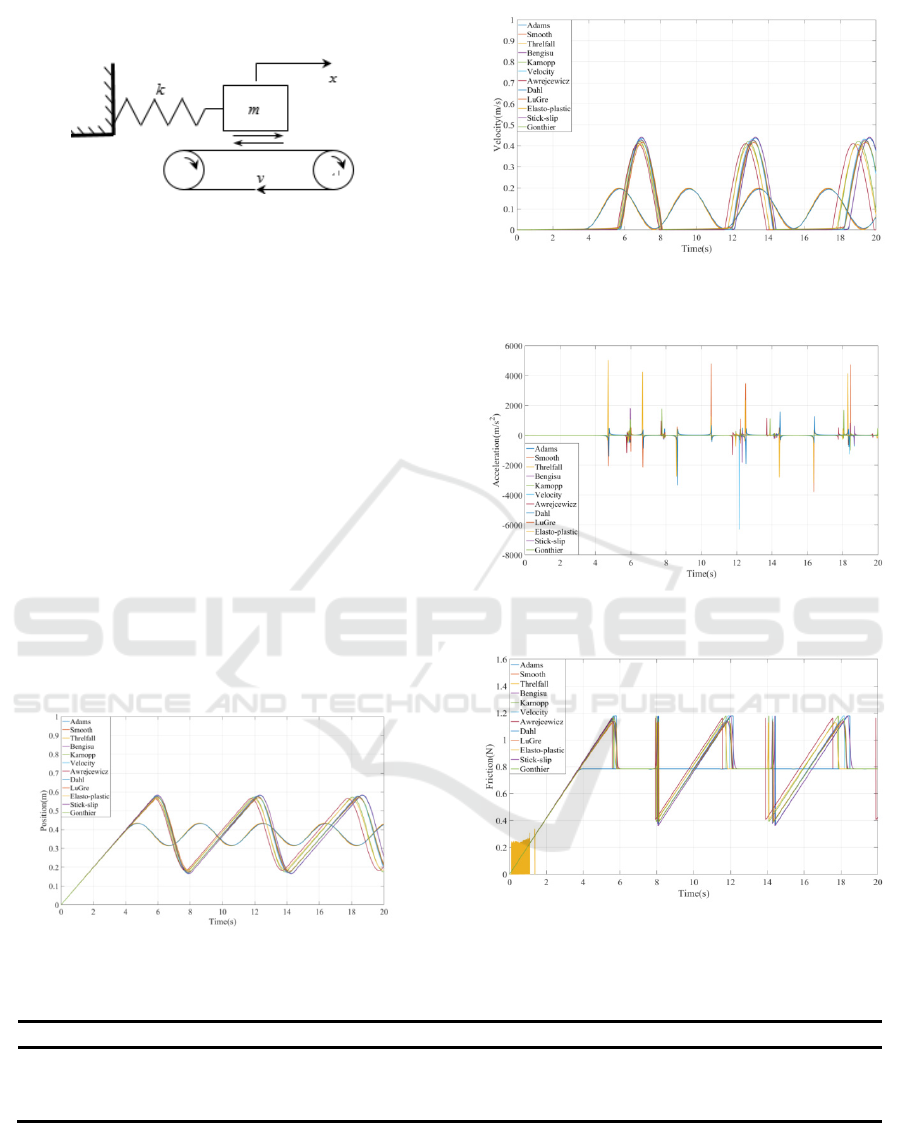
simplified model structure is shown in Fig. 1.

Fig 1. Diagram of the mechanism.

The belt rotates at a constant speed v in the

Rabinowicz case, and the block moves under the

combined action of friction and the tension of spring.

When the tangential force namely the spring tension

is less than the static friction, the slider is static. At

this time, it should be in the stage of pre-sliding and

static friction. When the tension force of the spring

is greater than the static friction, the friction

decreases with the increase of the relative velocity,

that is “Stribeck effect”. Meanwhile, the block

begins to be in sliding until the tension force of the

spring is less than the static friction again, and the

process of motion begins to cycle. The parameters of

each component in the mechanism are shown in

Table 2, and the reference of the parameters

involved in each model is shown in Table 3. The

curves of the relative displacement, the relative

velocity, the relative acceleration and the friction

with time are respectively drawn in Fig. 2~ Fig. 5.

Fig 2. Relative displacement of the body.

Fig 3. Relative velocity of the body.

Fig 4. Relative acceleration of the body.

Fig 5. Friction of the body.

Table 2. Rabinowicz model parameters.

Name Value Name Value

Mass (m) 0.8 kg

Step size(



-6

Belt velocity(v) 0.1m/s Time step(t) 20s

Stiffness coefficient(k) 2.1N/m Integral method Runge-Kutta

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

254

Table 3 Friction model parameters for Rabinowicz case

Name Symbol Value Name Symbol Value

Dynamic friction

coefficient

0.1 Damping coefficient



190Ns/m

Static friction coefficient u

0.15 Adhesion coefficient



0 Ns/m

Velocity error v

-3

m/s Breakaway displacement z

-7

Stribeck velocity v

-3

m/s Maximum deformation z

max

-6

Stiffness coefficient



N/m Dwell-time constant



0.1

From Fig.2~ Fig.5 it can be seen that when the

Coulomb model, the Threlfall model, and the Dahl

model is adopted for the Rabinowicz case, the

dynamic characteristics and the friction of slider in

the mechanism with only prismatic joints are very

similar, and the most of friction phenomena cannot

be found except the dynamic friction. Nevertheless,

the other models show the obvious process of the

viscous and sliding. The differences of

characteristics of the motion in the Rabinowicz case

with different friction models gradually increase

with time, which is mainly caused by the difference

of parameters contained in each friction model and

the accumulated error generated by the iterative

process. The integral adopts the ode15s that are

applicable to the dynamic friction model for the

Runge-Kutta method and the absolute error is 10-8.

Table 5 lists the calculation time used for each

model. In order to select the friction model that

satisfies the requirements of the frictional

characteristics in actual conditions, the stability of

the positional solution of each model is calculated

by the equation (1), and the friction model that can

meet the specific phenomenon in friction is sorted

by the efficiency (t) and stability (s). The results are

shown in Table 5, in which J stands for the static

friction, S stands for the "stribeck effect", and Y

stands for the pre-sliding.



1,2,3,...,11









(1)

Where xi represents the solution of position,

represents the average value of the position, ni

represents the number of solutions and i is the

number of friction models.

Table 4. The time and position stability of friction models.

Name T(s) S(×10

)

Smooth 2.6988 12.7889

Threlfall 2.7909 11.6026

Bengisu 2.6242 13.8757

Karnopp 2.3851 13.9528

Velocity-based 2.1976 13.8141

Awrejcewicz 2.3762 12.5478

Dahl 9.6875 13.4439

LuGre 11.3336 15.0088

Elasto-plastic >100 14.5011

Stick-slip 10.4979 13.3829

Gonthier 16.7579 14.6707

Table 5. Comparison of selection order for various friction phenomena.

Name

J S Y J+S J+S+Y

t s t s t s t s t s

Smooth

Threlfall

Bengisu

④ ④ ① ②

① ②

Karnopp

③ ⑤

Velocity

① ③

Awrejcewicz

② ①

Dahl

① ①

LuGre

⑥ ⑧ ③ ⑤ ② ④

① ③

Elasto-plastic

⑧ ⑥ ⑤ ③ ④ ②

③ ①

Stick-slip

⑤ ② ② ①

② ①

Gonthier

⑦ ⑦ ④ ④ ③ ③

② ②

Investigation of Selection Mechanism of Friction Models in Multibody Systems

255

When the static friction phenomenon is only

required to be observed in the Rabinowicz case, it

can be seen from Table 6 that if the efficiency of

calculation is firstly considered the Velocity-based

model should be selected, and if the stability is a

priority the Awrejcewicz model should be chosen

first. When the "stribeck effect" only needs to be

observed in practice, the Bengisu model should be

chosen first for computational efficiency but the

Stick-slip model for stability. The Dahl model can

be selected directly when the pre-sliding is only

considered in actual conditions. Similarly, when the

static friction and the "stribeck effect" need to be

observed at the same time, the first choice is the

Bengisu model for the computational efficiency, and

for the stability of position the first choice is the

Stick-slip model. Finally, if three friction

phenomena mentioned above all need to be

described at the same time the LuGre model should

be selected when the efficiency of calculation is

considered firstly, but the Elasto-plastic model

should be chosen in consideration of the data

stability.

4.2 Model with Prismatic and Revolute

Joints

Summarizing the structural features of the two cases

before, the single pendulum box both with revolute

joints and prismatic joints is considered as the

research object. The effects of different friction

models on the motion characteristics of the two

components in the single pendulum box are studied.

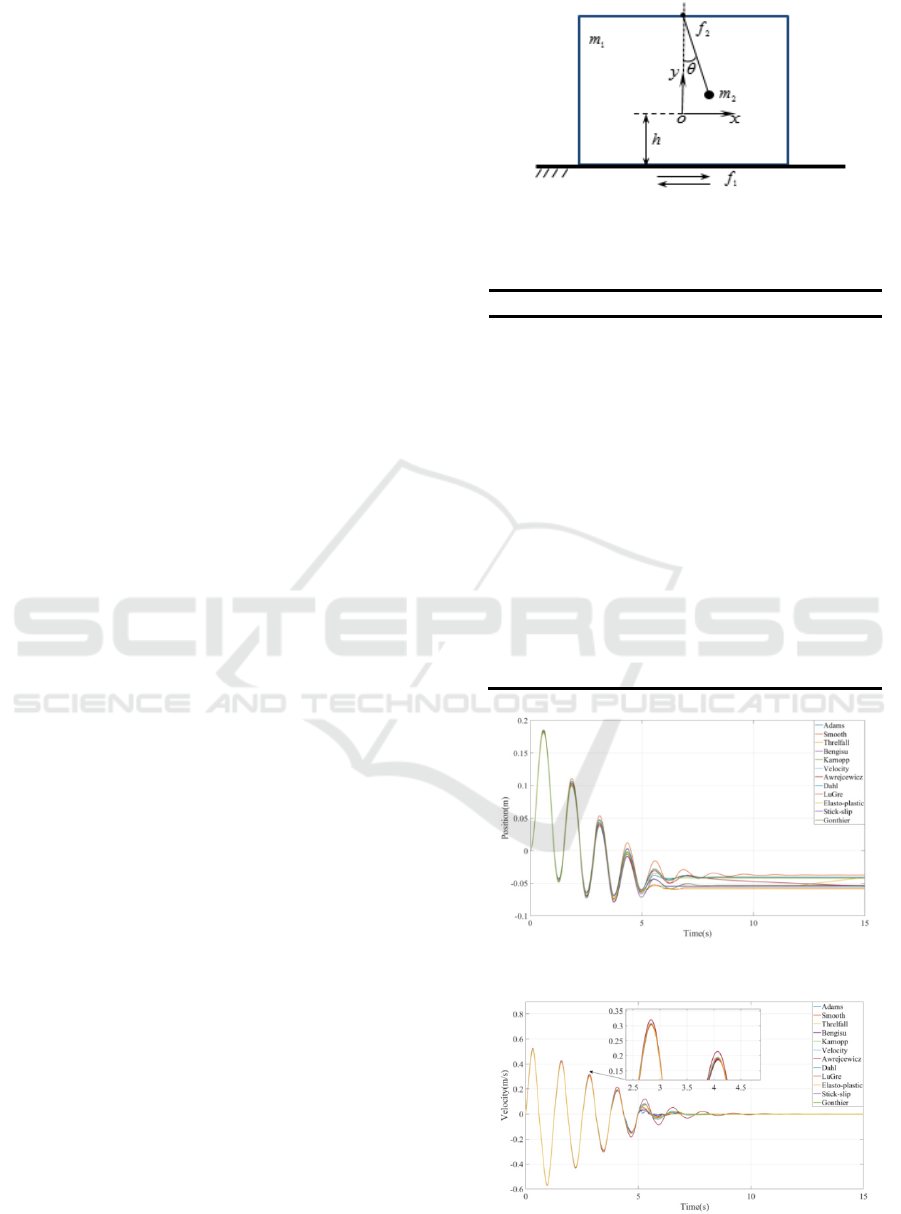
The schematic diagram of the mechanism is shown

in Fig. 6, and the parameters of each component in

the single pendulum box are shown in Table 10. The

pendulum hangs on the midcourt line on the top of

the box, the initial angle is 30° and the distance to

the ground from the body center of mass is h. The

free swing of the single pendulum drives the box to

slide left and right and finally comes to rest.

Considering the frictional force of the prismatic and

revolute joints at the same time, the box appears to

be the viscous and sliding as its velocity approaches

zero. See Fig.6 ~ Fig.12 for its characteristic curves

in motion.

Fig 6. Simple diagram of simple pendulum box.

Table 6. Simple pendulum box parameters.

Name Value Name Value

Box

mass(m

)

6 kg

Initial

angular

(



)

30°

Box

moment(I

)

0.1

kg.m

Initial

position

(pendulum)

[0,0.4]

The height

of center

of mass(h)

0.2m

Pendulum

moment(I

)

1.8

kg.m

Initial

position

(Box)

[0,0]

Step size(t)

-6

Pendulum

mass(m

)

20 kg Time step(t) 15s

Rod

length(L)

0.3m

Integral

method

Runge-

Kutta

Fig 7. Relative displacement for the box.

Fig 8. Relative velocity for the box.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

256

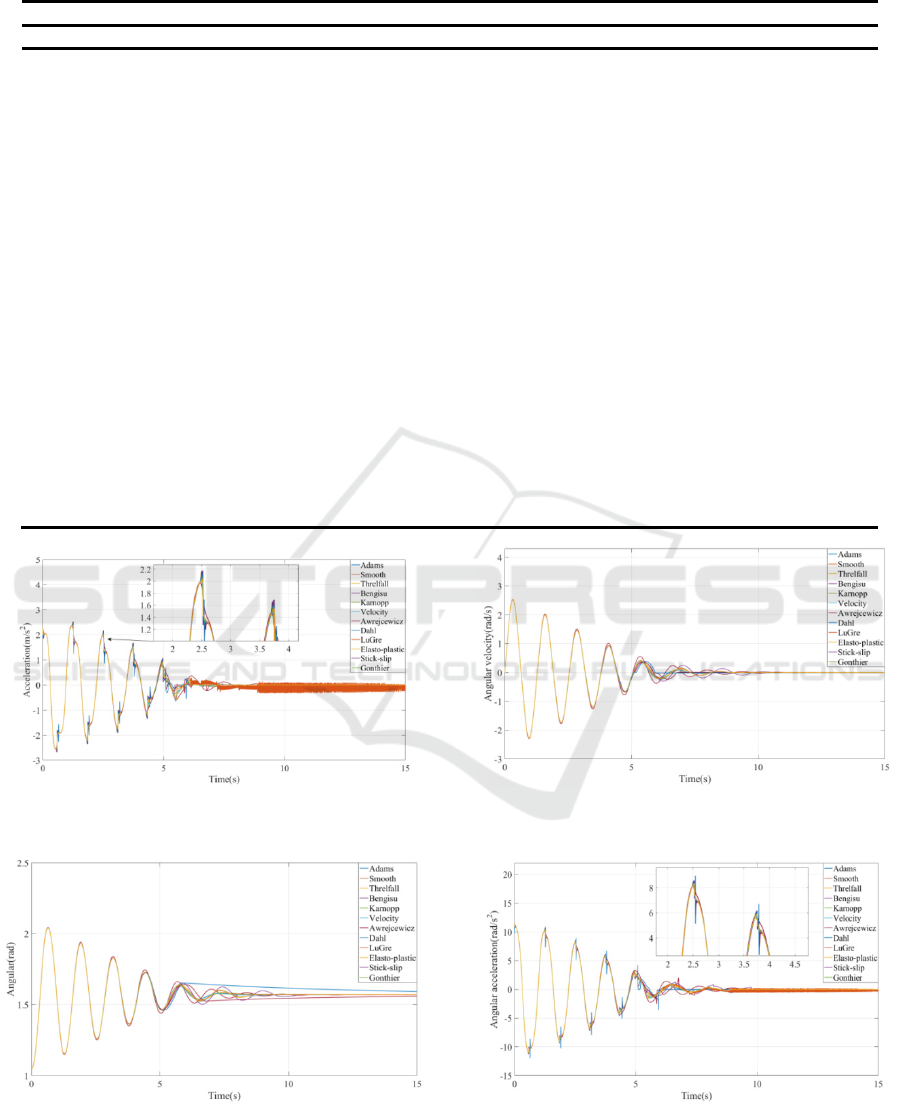
Table 7. The friction model parameters for Simple pendulum box.

Simple pendulum Box

Name Symbol Value Name Symbol Value

Dynamic

friction

coefficient

0.002

Dynamic friction

coefficient

0.02

Static friction

coefficient

0.003

Static friction

coefficient

0.03

Velocity error v

-2

m/s Velocity error v

0.06m/s

-3

m/s v

0.0005

-3

m/s v

-3

m/s

Stribeck

velocity

str

-3

m/s Stribeck velocity v

str

-3

m/s

str

-5

m/s(Gon) v

str

-5

m/s(Gon)

Stiffness

coefficient



N/m Stiffness coefficient



N/m

Damping

coefficient



2Ns/m Damping coefficient



2Ns/m

Adhesion

coefficient



0 Ns/m Adhesion coefficient



0 Ns/m

Breakaway

displacement

-7

Breakaway

displacement

-7

Maximum

deformation

max

-7

Maximum

deformation

max

-7

Dwell-time

constant



0.01 Dwell-time constant



0.01

Fig 9. Relative acceleration for the box.

Fig 10. Relative angular for the pendulum.

Fig 11. Relative angular velocity for the pendulum.

Fig 12. Relative angular acceleration for the pendulum.

Investigation of Selection Mechanism of Friction Models in Multibody Systems

257

Table 8. The time and position stability of friction models.

Name T(s) S(×10

)

Smooth 3.5109 5.8842

Threlfall 4.3273 6.4755

Bengisu 5.8561 6.7982

Karnopp 6.5503 7.0905

Velocity-based 8.3748 3.7149

Awrejcewicz 6.1151 7.1542

Dahl 45.3545 6.8376

LuGre 76.8279 6.2963

Elasto-plastic 229.0278 3.3126

Stick-slip 99.3741 1.4088

Gonthier 129.9982 5.3765

Table 9. Comparison of selection order for various friction phenomena.

Name

J S Y J+S J+S+Y

t s t s t s t s t s

Smooth

Threlfall

Bengisu

① ⑥ ① ⑤

① ②

Karnopp

③ ⑦

Velocity

④ ③

Awrejcewicz

② ⑧

Dahl

① ④

LuGre

⑤ ⑤ ② ④ ② ③

① ③

Elasto-

plastic

⑧ ② ⑤ ② ④ ①

③ ①

Stick-slip

⑥ ① ③ ①

② ①

Gonthier

⑦ ④ ④ ③

③ ②

② ②

The single pendulum box is a kind of mechanism

in which the sliding block is driven to back and forth

by the weight component of the pendulum. In the

whole process of moving, the friction model is

coupled with the mechanical system, which is

because the friction in the prismatic joints and the

friction in revolute joints are both considered. From

Fig. 7 to Fig. 9, it can be seen that the static friction

model and the dynamic friction model have little

influence on the relative position and velocity of the

box, but the acceleration has an obvious error and

appears big fluctuation. See Fig.10 to Fig.12, it is

found that the relative angle, the relative angular

velocity and relative angular acceleration of the

single pendulum in the selection of the LuGre model

and the Elasto-plastic model have obvious errors at

the end of the motion. The same as two cases above,

the best choice of each friction model for the

specified friction phenomenon can be obtained by

sorting the efficiency of calculation and the stability

of position. The following conclusions can be

obtained by comparing the select method of the

three cases:

(1) For the single pendulum box, it is different

from the previous two cases when the static friction

phenomenon is only required to be observed in

actual conditions. If the efficiency of calculation is

taken first, the Bengisu model should be selected; if

the stability is taken first, the Stick-slip model

should be taken.

(2) When the actual conditions only need to

observe the "stribeck effect", the selection of the

friction model is the same as the Rabinowicz case.

When the pre-sliding is only needed to be

considered, the Dahl model was selected owing to

the computational efficiency has little influence on

the variation of the kinds of the joint in the

mechanism and remained the highest effect all the

time. When the stability of position is considered

first, the select method of the single pendulum box is

the same as the Rabinowicz case, namely, the

Elasto-plastic model should be selected.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

258

(3) When the static friction and the "stribeck

effect" need to be observed at the same time or the

three kinds of friction phenomena mentioned in the

previous section need to be observed simultaneously,

the change of the prismatic joints and the revolute

joints in the mechanism has no influence on the

selection of friction model. Considering the

difficulty of parameter selection, it is generally

preferred the LuGre model in actual conditions.

5 CONCLUSION

In this paper, six static friction models and five

dynamic friction models are briefly reviewed for the

problem of dynamic performance affected by the

different friction models. Two kinds of mechanisms

including a model with prismatic joints and model

both with prismatic joints and revolute joints were

tested, the dynamic simulation of the three cases was

conducted and the change curve was drawn. The

numerical solution is compared with ADAMS, and

the analysis shows that:

(1) According to the special requirements of

friction phenomena in practical application, the

selected order of friction models discussed in this

paper is different when the multibody system

includes different joints, especially in considering a

certain friction phenomenon. Only fewer friction

models can be selected when need to describe more

friction phenomena. This is a very important reason

to limit the selected order of friction model when the

multibody system includes different kinds of joints,

such as only including prismatic joint or including

revolute joint and prismatic joint simultaneously.

(2) Compared to the static friction models, the

dynamic friction models own favorable continuity

when the multibody system contains different kinds

of joints. It is more important that the dynamic

friction models can better depict the nonlinear

behavior such as the pre-sliding, the "Stribeck

effect", the static friction and the viscous- sliding.

(3) Regarding the multibody system only

includes prismatic joints, the effect of different kinds

of friction modes on its dynamic response is not

obvious. When the multibody system simultaneously

includes prismatic joints and revolute joint, the

effect of dynamic friction model on the acceleration

is significant.

(4) Due to the dynamic friction model involves a

lot of parameters and has a significant influence on

the multibody system with revolute joint, in order to

improve the computational accuracy and the stability

of calculated results, hence, the dynamic friction

model should avoid being selected in the multibody

system with revolute joint. However, the LuGre

model is the best choice when the more friction

phenomena need to be studied.

In order to eliminate the adverse factors caused

by the friction to improve the dynamic performance

of the mechanical system, the effects of different

friction models on the characteristics in the motion

of the multibody systems with prismatic joints and

revolute joints are considered in this study.

According to the computational efficiency and the

stability of different friction models in different

mechanisms, the optimal friction model with

different kinds of joints in multibody systems is

obtained. Different multibody systems select

different friction models according to the actual

conditions, the computational efficiency and the

stability of simulation results. The friction model

with different kinds of joints is a very important

factor for the results of the dynamic calculation. The

qualitative analysis of different friction models in

the dynamic characteristics of the mechanisms with

different kinds of joints provides an important

theoretical basis for the following study of dynamics

in multibody systems with clearance and collision.

ACKNOWLEDGEMENTS

The authors is supported by research fund for the

doctoral program of Longdong University. (No.

XYBY1906).

REFERENCES

Ambrósio Jorge A.C. Impact of Rigid and Flexible

Multibody Systems: Deformation Description and

Contact Models [J]. Virtual Nonlinear Multibody

Systems, 2003.

Armstrong-Hélouvry B., Canudas Dewit, C: Friction

modeling and compensation, The Control Handbook,

Boca Raton: CRC Press, 1995.

Awrejcewicz Jan, Fečkan Michal, Olejnik Pawel. On

continuous approximation of discontinuous systems

[J]. Nonlinear Analysis: Theory, Methods &

Applications, 2005, 62(7): 1317-1331.

Awrejcewicz J. Chaotic motion in a nonlinear oscillator

with friction [J]. Ksme Journal, 1988, 2(2): 104-109.

Awrejcewicz J, Grzelczyk D, Pyryev Yu. On a Novel Dry

Friction Modeling: Differential Equations

Computation and Lyapunov Exponent Estimation[C].

Topics on Chaotic Systems - Selected Papers from

CHAOS 2008 International Conference, 2009: 22-30.

Investigation of Selection Mechanism of Friction Models in Multibody Systems

259

Bengisu M. T., Akay A. Stability of Friction-Induced

Vibrations in Multi-Degree-of-Freedom Systems [J].

Journal of Sound & Vibration, 1994, 171(4): 557–570.

Benson David J., Hallquist John O. A single surface

contact algorithm for the post-buckling analysis of

shell structures [J]. Computer Methods in Applied

Mechanics & Engineering, 1990, 78(2): 141-163.

Berger Ej. Friction modeling for dynamic system

simulation [J]. Applied Mechanics Reviews, 2002,

55(6): 25--32.

Cha Ho Young, Choi Juhwan, Han Sik Ryu, et al. Stick-

slip algorithm in a tangential contact force model for

multi-body system dynamics [J]. Journal of

Mechanical Science & Technology, 2011, 25(7):

1687-1694.

Coulomb P.C.A. Theorie des machines simple s [M].

Bachelier: 1821.

Dahl P. R. A Solid Friction Model [J]. Aerospace Corp El

Segundo Ca, 1968.

De Wit C. Canudas, Olsson H, Astrom K. J, et al. A New

Model for Control of Systems with Friction [J]. IEEE

Transactions on Automatic Control, 1995, 40(3): 419-

425.

Duan Chengwu, Singh Rajendra. Dynamics of a 3dof

torsional system with a dry friction controlled path [J].

Journal of Sound & Vibration, 2006, 289(4): 657-688.

Dupont P., Armstrong B., Hayward V. Elasto-plastic

friction model: contact compliance and stiction[C].

American Control Conference. Acc, 2002: 1072-1077

vol.2.

F. S, A X, Cieszka, et al. The importance of static friction

characteristics of brake friction couple, and methods

of testing [J]. Lubrication Science, 2010, 3(2): 137-

148.

Gonthier Yves, Mcphee John, Lange Christian, et al. A

Regularized Contact Model with Asymmetric

Damping and Dwell-Time Dependent Friction [J].

Multibody System Dynamics, 2004, 11(3): 209-233.

Karnopp D. Computer Simulation of Stick-Slip Friction in

Mechanical Dynamic Systems [J]. Trans.of the Asme

J.dyn.syst.meas.control, 1985, 107(1): 100-103.

Leine R. I., Campen D. H. Van, Kraker A. De, et al. Stick-

Slip Vibrations Induced by Alternate Friction Models

[J]. Nonlinear Dynamics, 1998, 16(1): 41-54.

Marques Filipe, Flores Paulo, Pimenta Claro J. C., et al. A

survey and comparison of several friction force

models for dynamic analysis of multibody mechanical

systems [J]. Nonlinear Dynamics, 2016, 86(3): 1407-

1443.

Threlfall D. C. The inclusion of Coulomb friction in

mechanisms programs with particular reference to

DRAM au programme DRAM [J]. Mechanism &

Machine Theory, 1978, 13(4): 475-483.

Wojewoda J, Stefański A, Wiercigroch M, et al. Hysteretic

effects of dry friction: modelling and experimental

studies [J]. Philosophical Transactions Mathematical

Physical & Engineering Sciences, 2008, 366(1866):

747-765.

Xie Youbo. Research on the status quo and devel-opment

strategy of tribology science and engineeri-ng

application [M]. Higher Education Press, 2009.

ICVMEE 2019 - 5th International Conference on Vehicle, Mechanical and Electrical Engineering

260