Performance of Crossflow Wind Turbine by the Variation of Blade

Slope and Diameter Ratio

Diniar Mungil Kurniawati, Aprian Dwi Prasetyo, Gad Gunawan and Illa Rizianiza

Institut Teknologi Kalimantan

Keywords: Blade slope, Crossflow, Diameter ratio, Performance

Abstract: Crossflow wind turbines have a good ability to capture wind, so it is very suitable to be developed in areas

with low wind speeds. The efficiency of a crossflow wind turbine is taken from two sides, so its turbine has

high efficiency. The first side is when the wind enters the turbine pushes the front face of the blade, and the

second side is when leaving the turbine, the wind pushes the rear face of the blade. In designing a crossflow

wind turbine, design parameters can affect the height or low performance of the turbine. The main objective

of this study was to determine the flow characteristics and performance of crossflow wind turbines. The

turbine is designed with a diameter ratio of 0.5 and a blade slope of 90˚. The number of blades used as a test

is 18 blades. Turbines were simulated with at 3 m / s of wind speed on TSR 0.1 – 0.5. The results obtained

from this study are wind flow visualization and cross-flow wind turbine performance parameters. The

crossflow wind turbine performance parameters are power coefficient, moment coefficient, and tip speed

ratio.

1 INTRODUCTION

Nowadays, much development is being carried out

on vertical axis wind turbines placed on the roofs of

high rise buildings. The idea was developed because

urban communities consume a lot of electricity so

that alternative energy is needed to overcome the

swelling of the use. TASV research has several

advantages in the form of construction with

relatively low cost, operating at a low tip speed, and

does not require high wind speeds to spin (Latif,

2013). The main advantage of TASV is that the

turbine does not have to be directed towards the

wind to be effective so that it is suitable for areas

with varying wind directions. TASV consists of

several types of rotors, one of which is a crossflow

type wind turbine. The crossflow rotor type of wind

turbine is a vertical wind turbine with a simple type

of rotating wheel due to the force of drag (Dharma,

2016).

In the design of wind turbines, there are several

design parameters that can affect the performance

of the turbine, including the number of blades,

geometric design, wind speed, and the shape of the

turbine blades. Geometry design is still an

interesting concern for the design development of

crossflow wind turbines. Turbine geometry is

expressed in the form of aspect ratio. The aspect

ratio is the ratio between the outer diameter and

inner diameter of the turbine or the ratio of the

outer diameter and height of the turbine. The effect

of aspect ratio on the performance of a wind

turbine can increase the power coefficient.

Savonius type vertical axis wind turbines with

greater aspect ratio show good performance due to

low losses (Mahmoud, 2012). Similarly, a

crossflow wind turbine that has an aspect ratio of

the outer diameter of the turbine to a large turbine

height (D / H) has low losses (Akwa et al., 2012).

The influence of geometry design on crossflow

wind turbines has a very important role in

performance. One of the influential geometry

designs is the diameter ratio. The diameter ratio in

the crossflow wind turbine is the ratio between the

diameter of the inside and the outside diameter. In

making cross-flow wind turbines with diameter

ratio variations of 0.58, 0.63, 0.68 and 0.73 where

each variation is tested with wind speeds of 2 m / s

and at TSR 0.1-0.4 with intervals of 0, 1 Turbines

with a diameter ratio of 0.68 and number of blades

of 20 produce the highest power coefficient of 0.5

at TSR 0.3 (Purbaningrum, 2016).

The number of blades affects the turbine

solidity. Turbines with a certain number of blades

will produce a good performance. High turbine

Kurniawati, D., Prasetyo, A., Gunawan, G. and Rizianiza, I.

Performance of Crossﬂow Wind Turbine by the Variation of Blade Slope and Diameter Ratio.

DOI: 10.5220/0009405200520057

In Proceedings of the 1st International Conference on Industrial Technology (ICONIT 2019), pages 52-57

ISBN: 978-989-758-434-3

solidity produces low CP and vice versa. Low

solidity indicates a higher tip speed ratio. At a low

TSR, the blade does not strongly affect the flow of

air through the wind surface area. Increasing the

number of blades in savonius wind turbines results

in low rotor torque. Therefore the number of blades

must be increased (Qing'anli et al., 2016). A certain

number of blades is likely to benefit the rotor in

wind extraction (Akwa et al., 2008). The

determination of the number of blades is

determined based on the advantages and

disadvantages of the number of blades. Increasing

the number of blades will improve airflow and

reduce the number of blades, which leads to lower

friction between wind currents and turbine blades

(Mandis et al., 2008).

An experimental test on a cross-flow wind

turbine is carried out by varying the ratio of the

diameter and the number of blades. The variation

of the diameter ratio used was 0.58, 0.63, 0.68, and

0.73, while the variation in the number of blades

used was 16, 20, and 24. Testing was carried out at

wind speeds of 3 m / s to 4 m / s. Experimental test

results show that the configuration between the

diameter ratio of 0.68 and 20 blade number is the

best configuration that has a power coefficient of

0.049 and a torque coefficient of 0.185 (Susanto,

2017).

In addition to the diameter ratio, the

geometrical design that influences the performance

of the crossflow wind turbine is the slope of the

blade. The sop blade determines the direction of

angina coming, which can be extracted well by the

blade of the turbine. The slope of the turbine blade

is very influential on the power generated in the

wind turbine. One of the wind turbine designs by

varying the angle of the blade and the radius of the

blade's curvature is tested to determine its effect on

the power produced. The test results show that the

crossflow turbine with a 45º turbine blade tilt angle

produces greater power than the 60º and 90º blade

tilt angles under all curvature radius conditions.

While the turbine curvature radius has the

characteristics of each at each angle of the turbine

tilt. Crossflow wind turbines with a blade radius of

60 mm curvature at a 45 ° angle variation of the

blades produce a maximum power of 2.47 watts at

a wind speed of 4.31 m / s and a CP of 0.41 at a

TSR of 0.76 (Barriyah, 2016).

Wind turbine performance parameters are

represented in dimensionless numbers, CP, CT, and

TSR. CP, or commonly known as the power

coefficient, is the difference between measured

turbine power and theoretical turbine power. TSR

or tip speed ratio is the value of the difference

between the rotor tip speed and free wind speed.

For certain nominal wind speed, TSR will affect

the rotational speed of the rotor. Because of this

description, the research carried out focuses on the

angle of the blade, the ratio of the diameter and the

number of blades simulated at various wind speeds.

2 SIMULATION METHODS

Computational fluid dynamics (CFD) is the tool

used to determine the numerical solution of the

equation governing fluid flow and other physical

processes with the help of computer computing. The

principle is to complete the calculation of the fluid

flow equation in the form of certain covering the

desired area. The area is often called with cells, and

the process of division is called meshing. A cell

constitutes a control calculation that will be carried

out by the application. In each cell will The

calculation is done with domain restrictions and

boundary conditions that have been determined. This

principle is used in the calculation process by using

computer computing assistance (Hirsch, 2007).

Preprocessing is the process of defining the

geometry of the model to be a computational

domain, making the mesh and defining boundary

conditions in the research conducted. Pre-processing

is the first step in analyzing a CFD model. Before a

model can be analyzed, the geometry of the model

must be defined first into the computational domain.

Then make a meshing in accordance with the

geometry and analysis to be performed. Finally,

defining boundary conditions and the nature of the

fluid to be used. This information is used as a

solution to the problem of fluid flow that is defined

for each node in each cell. The accuracy of the

results of data processing by CFD is governed by the

number of cells in the grid. In general, a large

number of cells make CFD results have better

accuracy, but with computing costs, that also

becomes more. The following picture is a vertical

axis wind flow type turbine model used in this study

shown in Figure 1.

Figure 1. The model of Crossflow wind turbine

Performance of Crossﬂow Wind Turbine by the Variation of Blade Slope and Diameter Ratio

CFD solver is processing and calculation of the

conditions that have been set during pre-processing.

At this stage, a numerical computational process is

carried out using the finite volume numerical

method. The first step is the integration of the

governing equations of fluid along with all the

governing volumes of the domain. The equation is

then discretized, which involves the substitution of

various finite difference approaches to the integrated

flow equation so that the integral equation can be

converted into algebraic equations. The equation is

then solved using the iteration method, so a solution

is obtained.

The domain stage is the domain formation in the

crossflow type wind turbine geometry model. There

are two forms of domains, namely rotating domains

and static domains. The rotating domain is located in

the outer diameter of a circular wind turbine, and

this domain is used as a path in the rotating motion.

The fixed domain or static domain, which functions

as the location of the fluid flow, this domain does

not move, as shown in the following Figure 2.

Figure 2. The domain of the wind turbine modeling

The results of the study were validated by 2D

modeling to ensure that the modeling created was an

accurate representation of the real phenomenon

being modeled. The domain used at the time of the

study was divided into two parts, namely the fixed

domain and the rotating domain. The shape of the

fixed domain is a rectangle with a length of 15000

mm and a width of 7500 mm. The rotating domains

are circular in diameter in accordance with the

research wind turbines; namely, crossflow type wind

turbines and rotating domains are located on the axis

of symmetry fixed domain with a distance of 2500

mm from the inlet or the left end.

Post-processing is the final step in CFD analysis.

At this stage, the results of the numerical

computations that have been made are visualized

and documented in the form of images, curves, and

animations.

The stage of meshing involves the division of

objects into smaller parts. To obtain an accurate

simulation, the meshing was made according to the

predicted flow pattern changes that will occur. The

following were the meshing processes (Figure 3).

Figure 3. The meshing pattern of the turbine

The process of meshing aims to divide the

solution domain into smaller parts. The amount of

this division will determine the accuracy of the

results of numerical computations performed. The

finer the meshing results, the results of numerical

computation will be more accurate later, but the

numerical computation time will be relatively

longer. The quality of triangular meshing can be

measured using a metric mesh.

The energy available in the wind is the kinetic

energy of most of the mass of air that moves above

the earth's surface. Wind turbine blades receive

kinetic energy and then convert it into mechanical or

electrical energy depending on end-use. The

efficiency of converting wind to other useful forms

of energy depends on the efficiency with which the

rotor interacts with wind flow (Hau, 2006). Wind

power can be written with the following equation:

P = 1/2 ρ A v

The theoretical power available in the wind flow

is in Equation 4.1. Whereas turbines cannot change

the power of the wind as a whole. When the flow of

wind passes through the turbine, some of its kinetic

energy is transferred to the rotor, and the air leaves

the turbine. This efficiency is usually expressed as a

power coefficient (Cp). Thus, the power coefficient

of the rotor can be defined as the ratio between the

actual power available at the wind as follows :







2















A comparison between the actual torque

produced by the rotor with the theoretical torque

produced by the turbine was expressed by the torque

coefficient (CT). So CT was stated as follows.

ICONIT 2019 - International Conference on Industrial Technology







2

















The ratio between the tip rotor speed and wind

speed is expressed as a tip speed ratio (λ). So that,

 

















Where Ω is the angular velocity. The power

coefficient and torque rotor coefficient can vary with

the tip speed ratio. Optimal TSR is a condition

where the most efficient energy transfer occurs, and

the power coefficient is at its maximum point (CP

max).

3 RESULTS AND DISCUSSION

Torque Coefficient (CT) is one of the dimensionless

parameters useful to show the value of the moment

or torque in a wind turbine simulation. At the

beginning of the simulation, the situation is not

steady due to the iteration less is produced, and more

iteration is needed to achieve a steady-state. The

time taken for the torque coefficient value relatively

stable is taken in 10-15 s. From Figure 5 shown that

the research data taken for research starts from 10-

15 s.

Figure 5. Data of torque coefficient

It had been matter because the value is quite

stable so that the average value can be determined

used for further calculations. Here was the result of

simulation results cross-flow wind turbine with 18

blades and 90° blade slope with a diameter ratio of

0.5.

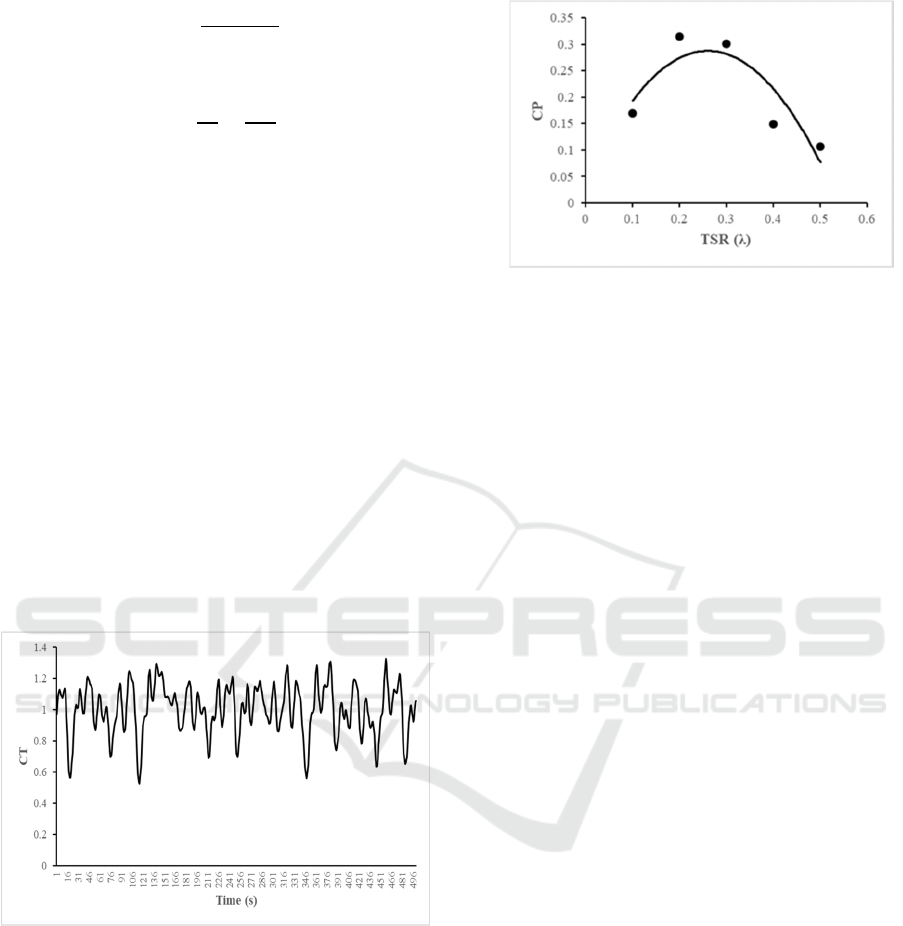
Figure 6. Data of power coefficient versus TSR

Choosing the right diameter and blade slope was

needed for the wind turbine to produce the best

power coefficient. The ratio of the diameter and

angle of the blade was very influential on the value

of the power coefficient due to the shape of the

blade that changes the shape of the blade so that it

can cause the amount of wind that hits the turbine

blade to not flow through a cross-section that is too

small or the wind can be hampered at a cross-section

that is too large and will cause pressure reverse and

can cause greater distance for energy transfer and

increase turbulence so as to cause a decrease in the

coefficient of power in the turbine. The selection of

the right diameter ratio is one important aspect in

producing a maximum power coefficient.

Rim radial is needed as the selection parameter.

If rim radial larger, then the amount of wind that hits

the blade will not be optimum because the wind

cannot pass through a cross-section that is too large,

which can cause back pressure so the power

coefficient value will be small. However, if the

width of the radial rim is too small, it will widen the

energy transfer distance so that it gets bigger and

increases turbulence, which causes the power

coefficient to decrease (Mockmore, 1949).

From the results of simulations, the rotational

speed of the turbine using an angle of 90° shown a

decreasing value because the turbine angle had more

upright. This is because the energy needed to move

the first level blade is not too large so that the energy

transmitted to crash into the next level blade will be

of great value as well.

However, at a more upright blade, the energy

needed to move the first level blade is greater so that

when it is forwarded to the second level blade, it will

be smaller so that it is likely that the flow of wind

does not crash at the second level blade. The blade

tilt angle variation is very influential and directly

proportional to the magnitude of the speed relative

to the blade and velocity (angle β), when the smaller

the angle of the blade tilt, the smaller the angle β.

Performance of Crossﬂow Wind Turbine by the Variation of Blade Slope and Diameter Ratio

The results of the study show that when the β

angle is small, the power generated is greater. This is

because the value of the absolute wind speed coming

out of the turbine is getting lower. When the wind

speed coming out of the turbine is low, it means that

the energy absorption carried out by the turbine is

getting maximum.

Figure 7. The flow contour of the cross-flow wind turbine

Figure 7 shows the speed contour produced by

the simulation process. The results of the speed

contour show that the process of extracting the

kinetic energy of the wind in the crossflow wind

turbine has a double interaction between the wind

and the blades of the wind turbine. The first

interaction occurred when the wind came in from the

inlet to the turbine so that it hits the first level blade.

Then the interaction of the two winds enters in the

wind turbine crevices and exits crashing into the

second level blades shortly before the wind exits

leaving the wind turbine.

In this wind turbine variation in the second level

blades, there is a lot of wind that is not well

extrapolated and more out of the turbine blades so

that the resulting performance is imperfect and not

better than other variations. This can happen

because, in the area of the second level, blades tend

to turn. The red areas in the next level blades

indicate an increase in speed in the blades. This, of

course, happens because of the large number of

blades and causes the blade gap to be narrow and the

presence of pressure, gravitational force, and viscous

friction on the turbine blade so as to produce high

speeds at several levels of blade crevices.

4 CONCLUSION

Based on the crossflow wind turbine simulation

results with a diameter ratio of 0.5, and the blade

slope is 90˚, the maximum CP value is 0.32 at TSR

0.2. Turbines in the back experience an increase in

speed caused by the flow of wind coming out of the

face of the turbine faster due to turbine rotation. In

the cross-flow wind turbine, there was negative

torque that caused the rotation speed of the turbine

hampered.

ACKNOWLEDGMENTS

The research was supported by Institut Teknologi

Kalimantan through PDB research grant , T.A. 2018,

REFERENCES

Akwa J.V., Júnior G.A.S, Petry A.P. 2012. Discussion on

the verification of the overlap ratio influence on

performance coefficients of a Savonius wind rotor

using computational fluid dynamics, Renewable

Energy Vol. 38, pp.141–149.

Barriyah, Kholifatul. (2016). “Uji Ekperimental Pengaruh

Sudut Kemiringan Sudu, Radius Kelengkungan Sudu

dan Kecepatan Angin Pada Turbin Cross Flow

Terhadap Daya yang Dihasilkan Pada Sistem

Pemulihan Energi yang Terintegrasi Dengan Menara

Pendingin”. Surakarta: Universitas Sebelas Maret.

Dharma, Untung S., dan Masherni. (2016), “Pengaruh

Desain Sudu Terhadap Unjuk Kerja Prototype Turbin

Angin Vertical Axis Savonius”, Jurnal Teknik Mesin

Univ. Muhammadiyah Metro Lampung, Vol. 5, No. 2,

Hal. 138-148.

Hau, E. 2006. Wind Turbines : Fundamentals,

Technologies, Application, Economics. New York :

Springer.

Latif, Melda. (2013). Efisiensi Prototipe Turbin Savonius

pada Kecepatan Angin Rendah. Jurnal Rekayasa

Elektronika Teknik Elektro Univertsitas Andalas, Vol.

10, No. 3, Hal. 147-152.

Mahmoud NH, El-Haroun AA, Wahba E, Nasef MH. An

experimental study on

improvement of Savonius rotor performance. Alex Eng J

2012;51(1):19–25.

Mandis, I.C., Robescu, D.N., Barglzan, M., Capitalization

of wind potential using a modified Banki wind

Turbine, UPB Scientifical Bulletin, Vol, pp. 70-4:

115-24.

Mockmore, C. dan F. Merryfield, (1949), The Banki

Water Turbine, Eng. Exp. Stn. Bull. Ser., vol. 25, no

February, pp. 1-28.

Purbaningrum, Pradityasari. (2016). “Studi Simulasi

Tentang Pengaruh Rasio Diameter dan Jumlah Sudu

ICONIT 2019 - International Conference on Industrial Technology

Terhadap Performa Turbin Angin Cross Flow Dengan

Menggunakan Software ANSYS-Fluent”. Surakarta:

Universitas Sebelas Maret.

Qing’an Li., Takao Maeda,. Yasunari Kamada., Kento

Shimizu,. Tatsuhiko Ogasawara., Alisa Nakai., Takuji

Kasuya., 2016. Effect of Rotor Aspect Ratio and

Solidity on A Straight-Bladed Vertical Axis Wind

Turbine in Three-Dimensional Analysis by The Panel

Method. Energy. Volume 121 (2017) 1-9.

Susanto, Sandi. (2017). “Uji Eksperimental pengaruh rasio

diameter rotor dan jumlah sudu terhadap performa

turbin angin crossflow”. Surakarta: Univeritas Sebelas

Maret.

Performance of Crossﬂow Wind Turbine by the Variation of Blade Slope and Diameter Ratio