Mass Transfer Modeling of Acid Violet 17 Adsorption onto Activated

Carbon

Puguh Setyopratomo, Hadiatni Rita Priyantini and Rudy Agustriyanto

Chemical Engineering Department, Faculty of Engineering, University of Surabaya, Raya Kalirungkut, Surabaya 60293

Keywords: Acid violet 17, Activated carbon, Dyes adsorption, Kinetic model.

Abstract: This study was conducted to determine the suitability of the observed equilibrium and kinetic model, as well

as the removal of acid violet 17. The batch experimental variables include the dyes initial concentration and

the ratio of the adsorbent mass to the volume of the solution. The adsorption equilibrium data were examined

using three equilibrium models i.e., Linear, Freundlich, and Langmuir. The observed model is limited by two

forms of the proposed kinetic model. The first model just considers the convection mass transfer of the dyes

to the external surface of the adsorbent, while the second model also takes into account the solute diffusion

in particles. The experiment result showed that the adsorption process follows the Langmuir correlation with

the adsorption capacity of 185.19 mg/g. From this study, it was found that the adsorption is controlled by the

diffusion stage inside the particle. The dyes removal reach 58%, which was achieved when 0.0015-gram

adsorbent was used per ml solution. The results of this study can contribute to the design of the commercial

scale adsorption process.

1 INTRODUCTION

In recent years, the production of dyes continues to

grow in line with the growth of the industries using

dyes as coloring agents such as paper, textile,

cosmetic, and leather tanning (Jain & Gogate, 2017).

At present, approximately 10 thousand dyestuff

products on the market (Goswami & Phukan, 2017).

The chemical structure of dyes is a complex aromatic

molecule. Besides, they contain various functional

groups. This causes toxic and non-biodegradable

properties (Yu et al., 2019). They are very stable, so

they tend to accumulate in nature. Globally, the

annual consumption of dyes in the chemical industry

reaches 7x105 tons, and it was estimated that 10-15%

of which was disposed into the water stream, causing

serious environmental pollution (Gamoudi & Srasra,

2019), (Belbel et al., 2018).

Acid violet 17 is the anionic azo dyes and is

usually used as a coloring agent for textile and leather

(Saleem, Pirzada & Qadeer, 2007). The biggest

source of dye contamination in the water stream is the

textile industry (Li, Mu & Yang, 2019). Disposal of

the dyes from industries to the water stream will cause

many environmental problems. The presence of dyes

in the water, even at low quantity, is undesirable. It

will decrease the beauty of the surroundings and

threatens human health and the environment

(Boudechiche et al., 2019). Besides, its presence in

the water body will reduce the penetration of light

needed for photosynthesis of aquatic biota (Daoud et

al., 2019).

It was reported that the intake of organic dyes into

the body could cause damage to several important

organs such as the liver, digestive system, and

nervous system of human beings (Gao et al., 2019).

Other harmful effects of dyes are carcinogenic,

mutagenic, and cause kidneys dysfunction (Abd-

Elhamid et al., 2019). Therefore, the removal of dyes

from the flow of industrial wastewater before being

discharged into a water body is a must.

There are several processing methods available to

eliminate dyes from wastewater, such as adsorption,

photocatalytic degradation, biodegradation,

coagulation-flocculation, ion exchange, membrane

technology, and electrochemical oxidation (Liu et al.,

2019). Among the processing methods for dyes

removal from liquid waste, adsorption is still

considered to be a more efficient and inexpensive

technology because the process is simple, operated at

ambient temperature and pressure, and cost-efficient

(Thinakaran et al., 2008), (Khorasani &

Shojaosadati, 2019).

Setyopratomo, P., Priyantini, H. and Agustriyanto, R.

Mass Transfer Modeling of Acid Violet 17 Adsorption onto Activated Carbon.

DOI: 10.5220/0009423701290136

In Proceedings of the 1st International Conference on Industrial Technology (ICONIT 2019), pages 129-136

ISBN: 978-989-758-434-3

129

Various adsorbents are available to remove dyes

from aqueous solutions such as clay, activated

carbon, clay, zeolite, carbon nanotubes, graphene

oxide, polymeric materials, and agricultural waste

(Rajabi, Mahanpoor & Moradi, 2019), (Vahdati-

Khajeh et al., 2019). In practice, the most widely used

adsorbent for removing dyes from aqueous solutions

is activated carbon (Ferreira et al., 2017). Besides

having high efficiency, activated carbon has an

economic advantage because it can be prepared from

agricultural waste materials that are rich in cellulose

and lignin (Herrera-González, Caldera-Villalobos &

Peláez-Cid, 2019).

Adsorption is one of the most important

separation technologies, where the dissolved

compound is selectively attracted to the surface of the

adsorbent through the mass transfer process resulting

in the accumulation of the compound at the surface or

the interphase of the adsorbent. Adsorption can occur

physically due to physical force such as hydrogen

bonding, polarity, Vander Waals forces, and dipole-

dipole interactions, etc., or chemically due to the

exchange of electrons, where adsorbate is chemically

bonded to the surface of the adsorbent (Kausar et al.,

2018). In the phenomenon of adsorption, the

interaction between solute and adsorbent is very

specific, and this depends on the mutual interactions

which are influenced by their physical and chemical

properties (Benabi et al., 2019).

In general, the mechanism of solute adsorption

from an aqueous solution to the surface of a solid

adsorbent consists of the following three successive

stages, i.e., 1) external mass transfer, where the solute

moves from the bulk solution to the outer surface of

the adsorbent particle; 2) intraparticle diffusion (pore

volume diffusion, surface diffusion, or a combination

of both mechanisms); 3) adsorption of the solute

molecules on an active site of the adsorbent

(Ocampo-Perez et al., 2010).

The adsorption reaction model, which is one of

the most widely used to represent dyes adsorption

kinetic onto activated carbon and includes pseudo-

first-order and pseudo-second-order, ignores both

external mass transfer and intraparticle diffusion

resistance. (Dotto, Buriol & Pinto, 2014). Thus this

model assumes that the adsorption kinetic is fully

controlled by the rate of adsorption of solutes on the

surface of the adsorbent. Therefore, this model

expressed the rate of adsorption as identical to the rate

of a chemical reaction (Ocampo-Pérez et al., 2012).

The consequence of using this model is that neither

the mass transfer coefficient nor the rate-controlling-

stage can be obtained. However, to obtain a design for

a reliable commercial-scale adsorption process

system, detailed and accurate information regarding

mass transfer resistance and the stage which controls

the adsorption rate are required. Therefore, in this

study, adsorption kinetic models will be developed to

determine the external as well as the intra-particle

diffusion mass transfer coefficient of acid violet 17

adsorptions onto activated carbon. To solve such an

adsorption kinetic model, the adsorption equilibrium

correlation at the interface between the solid phase

and the liquid phase is required. Hence the objective

of this study is 1) to determine the correlation of

equilibrium adsorption of acid violet 17 onto

activated carbon; 2) to determine the external and the

intra-particle diffusion mass transfer coefficients; 3)

to investigate the percent dyes removal.

2 THEORY AND EXPERIMENT

2.1 Equilibrium Adsorption

Correlation

Equilibrium adsorption correlation is the relationship

between solute concentration in the liquid phase and

solid phase at equilibrium at a certain temperature.

Three adsorption equilibrium models will be

investigated for their suitability with the adsorption

system studied in this study, namely: the Langmuir

model, the Freundlich model, and the Linear model.

The Langmuir equilibrium model is expressed in

Equation (1). The Langmuir model assumes: (1) the

adsorbent has a homogeneous active side and can

only adsorb one layer of the adsorbate molecule, (2)

there is no interaction between the absorbed

molecules, (3) the same mechanism occurs in each

adsorption process. The Freundlich model is stated in

equation (2). The Freundlich model assumes that the

adsorbent has a heterogeneous surface, and each

molecule has different absorption potential.

Meanwhile, related to Henry's Law, equilibrium in

solid-liquid systems can be described by linear

equilibrium. This linear equilibrium is limited to low

equilibrium concentrations, i.e., for solute

concentrations below 50 ppm. The formulation of

linear equilibrium is expressed in Equation (3).

(1)

eqmaxμ,maxμ,eqμ,



(2) KCC

1/n

eqeqμ,



(3) C HC

eqμ,eq



where, Cμ, eq: the mass of solute adsorbed per mass

of the adsorbent at equilibrium, Cμ, max: the

ICONIT 2019 - International Conference on Industrial Technology

130

theoretical monolayer saturation capacity, Ceq: solute

concentration in solution at equilibrium, k, K, n:

constant, H: a distribution constant.

2.2 Kinetic Model

In designing a system of adsorption processes, the

analysis of adsorption kinetic is a very important

stage. From the kinetic analysis, information about

the time needed to achieve the adsorption equilibrium

will be obtained. Furthermore, from the kinetic

analysis, the adsorption mechanism will be known

(Magdy & Altaher, 2018). Adsorption of solute in

porous particles will involve the following stages i.e.,

external mass transport, intra-particle diffusion, and

adsorption on an active site inside the pores.

(Ocampo-Perez et al., 2011). In this work, kinetic

models were developed on the basis of the following

general assumptions: (i) intraparticle diffusion occurs

by pore volume diffusion mechanism that follows

Fick's law of diffusion, (ii) adsorption reaction at the

surface of the adsorbent occurs instantaneously, (iii)

as an adsorbent, the activated carbon particles have a

spherical shape, (iv) within the adsorbent particles the

diffusion occurs only in the radial direction, (v)

adsorption takes place under isothermal conditions.

2.2.1 The First Kinetic Model

In the first kinetic model, solute adsorption is

considered to only occur from the bulk of the liquid

to the outer surface of the adsorbent. Thus there is no

gradient of solute concentration within the adsorbent

particles. At such condition, the rate of decreasing

mass of solute in the liquid phase is equal to the rate

of mass transfer of the solute from the bulk solution

to the outer surface of the adsorbent, and is

mathematically formulated in the following equation:



(4) CC



where: t: time, kc: the convection mass transfer

coefficient, A: the outer surface area of the adsorbent,

C: the solute concentration at the bulk of solution, C

*: the solute concentration at the liquid phase

interphase, Vl: total solution volume.

Meanwhile, the solute transfer rate from the

solution to the adsorbent is equal to the rate of solute

increase in the adsorbent, as stated in the following

equation.



(5) CC



Where: Cμ: solute concentration in the adsorbent,

mp: the mass of adsorbent. The initial condition are:

at t=0, C = Co and Cμ = 0. The correlation between

the concentration in the solid phase and in the liquid

phase at the interface follows the Langmuir model.

This correlation acts as a boundary condition.

2.2.2 The Second Kinetic Model

The second kinetic model assumes that the adsorbent

is a porous medium so that the mass solute transfer

occurs in three stages, namely: (1) convection of the

solute from liquid bulk to the outer surface of the

adsorbent through the film layer on the outer surface

of the adsorbent, (2) intraparticle liquid phase

diffusion of solute from the outer surface of the

adsorbent to the active site of the adsorbent through

the pore, (3) attachment of the solute to the active site

of the adsorbent in the pore.



(6) ρCεC

Δrr 4

Δrr4πD

r 4D

adsμ

Δrr













































(7)









































































ads









(8)

R 4πD CCR 4πk

surface

















In the second model, it is assumed that diffusivity

and porosity are uniforms in all parts of the adsorbent.

While, as in the first model, the equilibrium between

the solute concentration in the liquid and solid phases

at the interface follows the Langmuir model. The

second model was developed by applying the

principles of solute mass balance in the particle and

manifested in three differential equations i.e. equation

(6) which applicable at the middle of the solid

adsorbent, equation (7) which applicable at the center

of the solid adsorbent and equation (8) which

applicable on the surface of the adsorbent, where, C:

concentration of solute in the liquid which fills the

adsorbent pore, ρads :density of the adsorbent, ε:

porosity of the adsorbent, R: adsorbent radius, r:

position in adsorbent in radial system, De: the

effective diffusivity of the solute, CL: solute

Mass Transfer Modeling of Acid Violet 17 Adsorption onto Activated Carbon

131

concentration in the bulk of the solution, CL*: solute

concentration in the solution at the interface.

2.3 Experiment

The acid violet 17 was obtained from a local

chemical supplier. The activated carbon, having

particle size <100 µm and bulk density of 150 - 440

kg/m3, was purchased from Merck Millipore. In all

batch adsorption experiments, activated carbon and

acid violet 17 were mixed in 250 ml beaker while

stirring continuously at a constant speed, in which the

volume of acid violet 17 solution was 100 ml.

Experimental variables include: initial concentration

of acid violet 17 (75 ppm, 125 ppm, 175 ppm, 225

ppm, 275 ppm) and mass of activated carbon used

(0.1 g; 0.1125 g; 0.125 g; 0.1375 g; 0.15 g). The

concentration of acid violet 17 in solution at certain

times and equilibrium was measured using a UV-Vis

spectrophotometer - Agilent 8453.

3 RESULTS AND DISCUSSION

3.1 Equilibrium Analysis

In this study, the equilibrium condition was assumed

to be achieved by allowing the batch adsorption

process to take place overnight. In this study, an

investigation of three equilibrium models was carried

out, i.e., Langmuir, Freundlich, and linear

equilibrium. The plot of equilibrium data obtained

from the experiment and plot of equilibrium models

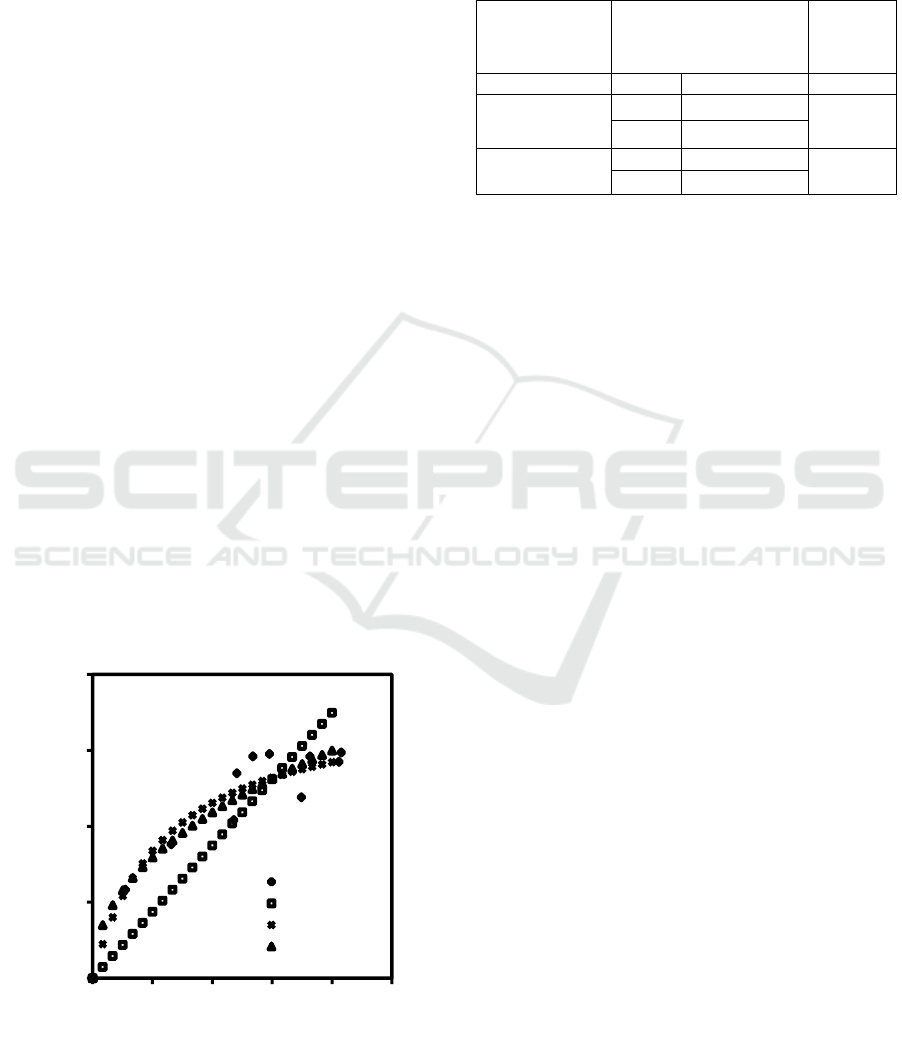
is presented in Figure 1.

Figure 1: Plot the experimental equilibrium data and the

equilibrium model.

The equilibrium parameters and the coefficient of

determination (R2) for each equilibrium model

observed for this system are presented in Table 1.

Table 1: The equilibrium parameters obtained for each

observed equilibrium model.

The observed

equilibrium

model

The equilibrium

parameters

Linear H 0.69 g/l 0.78

Freundlich

K 16.76

0.88

0.48

Langmuir

k 0,28 l/mg

0.93

,max

185.19 mg/g

From the coefficient of determination, it can be

concluded that the Langmuir equilibrium model is the

most appropriate for this system. This result has

shown that the adsorption process takes place on a

homogeneous solid surface, and the adsorbed dyes

form a monolayer on the surface of activated carbon.

Furthermore, based on Langmuir's equilibrium

parameters obtained from this experiment, it can be

seen that the maximum adsorption capacity of the

activated carbon is 185.19 mg/g.

3.2 Kinetic Analysis

Kinetic models that are often used to observe

adsorption kinetic include the pseudo-first-order and

pseudo-second-order equations. The advantage of the

model is that the equation is simple, but both models

ignore the mass transfer or diffusion step that occurs

in adsorption and only taking into account the rate of

attachment of the solute to the surface of the

adsorbent (Yao & Chen, 2018).

In contrast, in this study the rate of attachment of

solutes to the surface of the adsorbent was considered

to be very fast so that the rate of the adsorption was

controlled by the rate of solute transfer across the

liquid film to the outer surface of the adsorbent and/or

the rate of solute diffusion within adsorbent particles.

The governing equations for the mass transfer in

the liquid film and the intraparticle diffusion are

partial differential equations, as expressed in the first

and second kinetic models. To obtain the mass

transfer coefficient of the solute in the liquid film and

the effective diffusivity of the solute within the

particles, the two models, are solved numerically

using the Matlab program.

100

150

200

0306090120150

Cμ,eq, mg/g

Ceq, ppm

Data

Linear

Langmuir

Freundlich

ICONIT 2019 - International Conference on Industrial Technology

132

3.2.1 The Solution of the First Kinetic

Model

The kinetic solution, which is expressed as changes in

solute concentration in liquid bulk with respect to

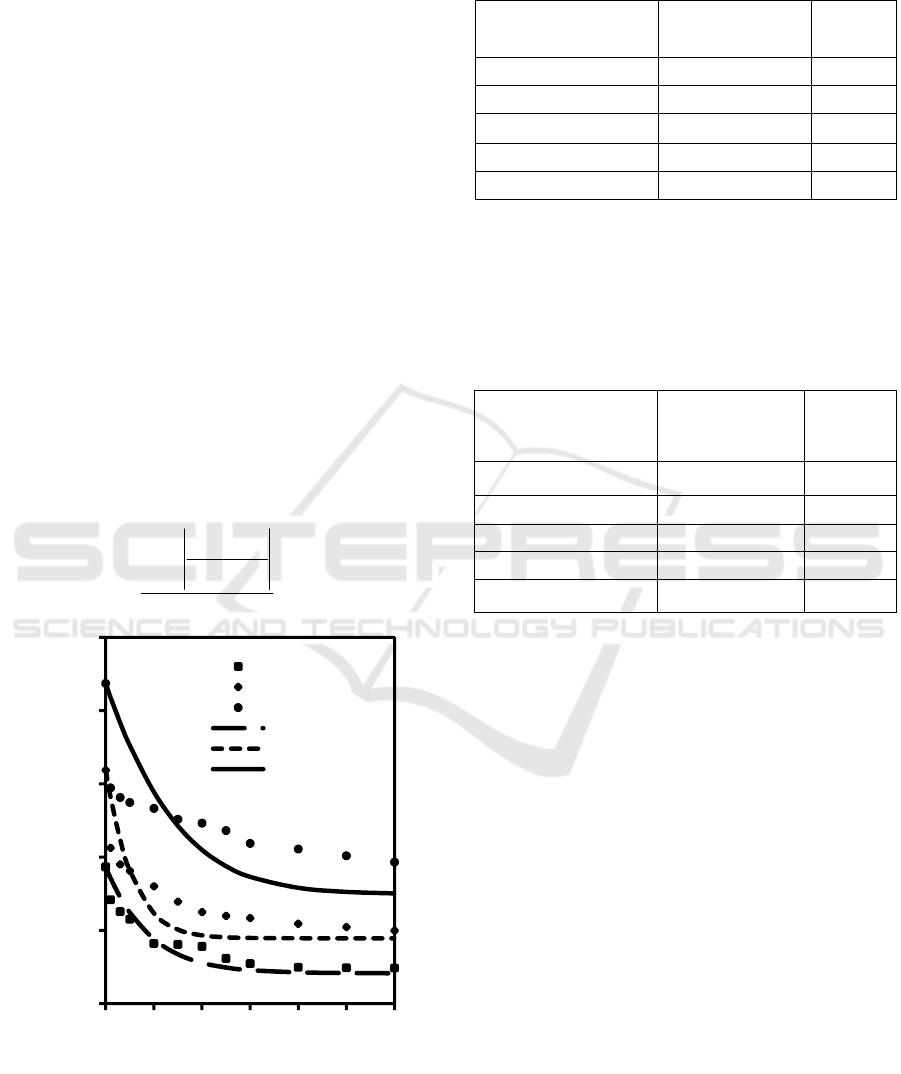
time, for the first model, is presented in Figure 2. The

solution applied the Langmuir model for the

calculation of concentration in the interface.

From Figure 2, it can be seen that for lower

concentrations, the first model kinetic is better suited

to this adsorption system. It is shown that for lower

solute concentrations, the results obtained from the

model are closer to the data obtained from the

experiment.

Meanwhile, the mass transfer coefficient of liquid

films (kc), obtained from the application of the first

kinetic model at an experiment with an adsorbent

mass 0.1 gram, was presented in Table 2.

The AAD parameter is the absolute average

deviation used to determine the level of suitability of

the model to experimental data. The AAD parameter

is defined in Equation 9, where: Ce = dyes

concentration obtained from the experimental result,

Cm = dyes concentration obtained from the observed

kinetic model, N = the number of the experimental

data.

(9)

AAD







Figure 2: Plot solute concentration in the liquid bulk versus

time at various initial solute concentrations. The results of

the first kinetic model were expressed as line, while the

experimental data were expressed as dot.

Table 2: Mass transfer coefficient at various solute initial

concentration applying the first kinetic model at an

experiment with an adsorbent mass 0.1 gram.

Meanwhile, the kc values at a various ratio of the

adsorbent mass to the solution volume are presented

in Table 3.

Table 3: Mass transfer coefficient at various ratio adsorbent

mass to solution volume applying the first kinetics model

when the initial solute concentration 275 ppm.

From the results obtained, it can be seen that the

change in solute concentration and the ratio of the

mass of adsorbent to the volume of solution does not

significantly influence the mass transfer coefficient.

The value of the mass transfer coefficient is in the

range of 8.38 x 10-5 - 1.97 x 10-4 cm/minute, with

the absolute average deviation in the range of 15.7%

- 25.1%.

3.2.2 The Solution of the Second Kinetic

Model

The value of the mass transfer coefficient and

effective diffusivity obtained by applying the second

kinetic model are presented in Table 4 for various

initial solute concentrations and Table 5 for the

various ratio of the mass of adsorbent to the volume

of solution.

Initial concentration

(ppm)

(cm/minute)

AAD

(%)

75 1.24 x 10-4 25.1

125 1.97 x 10-4 19.7

175 1.37 x 10-4 17.9

225 8.66 x 10-5 16.5

275 8.55 x 10-5 19.2

Ratio the adsorbent

mass to the solution

volume (g/ml)

(cm/minute)

AAD

(%)

0.001 8.56 x 10-5 15.7

0.001125 8.38 x 10-5 22.0

0.00125 1.05 x 10-4 23.2

0.001375 9.46 x 10-5 22.5

0.0015 8.78 x 10-5 22.6

120

160

200

0 102030405060

Solut concentration in liquid bulk (ppm)

Time(minutes)

data 75

data 125

data 175

75 ppm

125 ppm

175 ppm

Mass Transfer Modeling of Acid Violet 17 Adsorption onto Activated Carbon

133

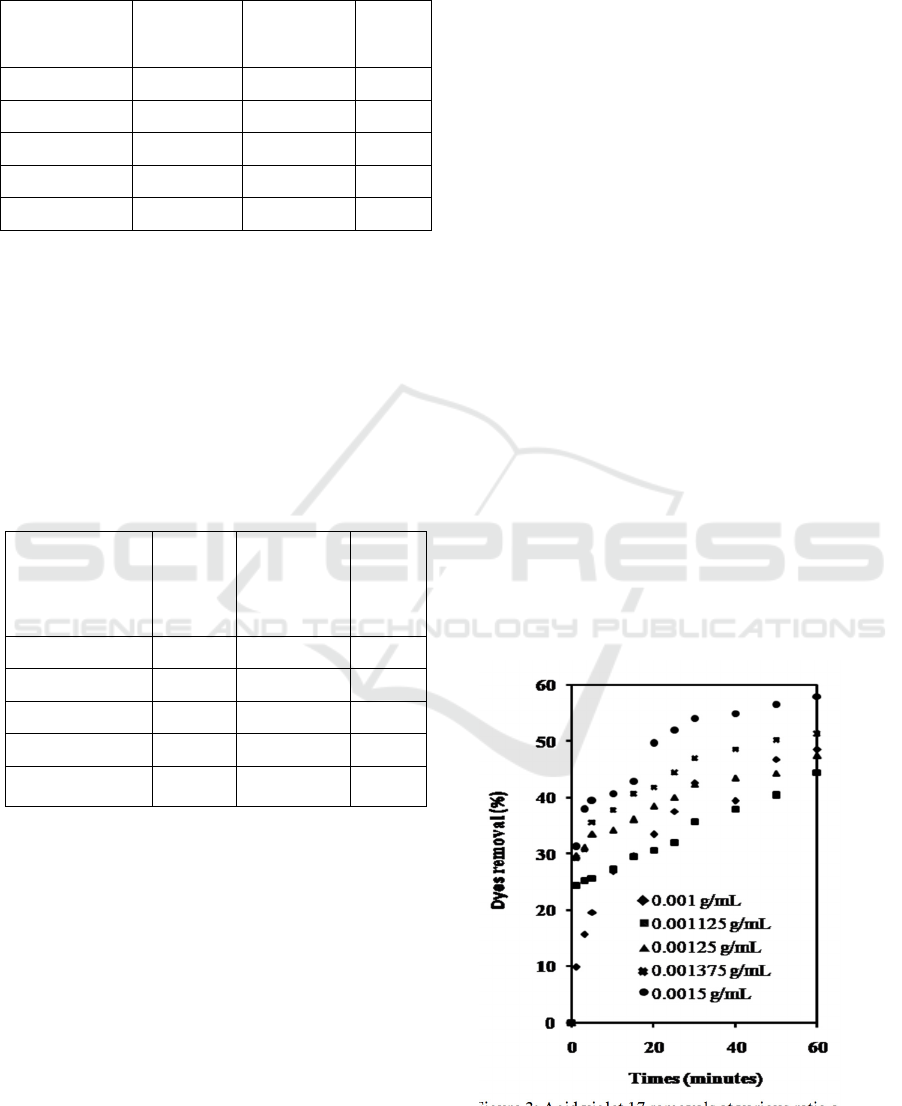
Table 4: The value of the mass transfer coefficient and

effective diffusivity obtained by applying the second

kinetic model for various initial solute concentrations.

Initial

concentration

(ppm)

cm/minute)

(cm2/

minute)

AAD

(%)

75 0.28 2.13 x 10-5 7.6

125 0.25 2.13 x 10-5 13.5

175 0.19 1.06 x 10-5 14.4

225 0.15 7.38 x 10-6 7.9

275 0.10 5.52 x 10-6 9.8

By applying the second kinetic model, the mass

transfer coefficient value tends to decrease with

increasing solute concentration. It also found that the

ratio of the adsorbent mass to the solution volume

does not have much effect on the mass transfer

coefficient.

Table 5: The value of the mass transfer coefficient and

effective diffusivity obtained by applying the second

kinetic model for the various ratio of the mass of adsorbent

to the volume of the solution when the initial solute

concentration 275 ppm.

Ratio

the adsorbent

mass to the

solution volume

(g/ml)

(cm/

minute)

(cm2/

minute)

AAD

(%)

0.001 0.13 6.54 x 10-6 4.1

0.001125 0.12 6.06 x 10-6 9.7

0.00125 0.11 8.22 x 10-6 12.6

0.001375 0.10 1.05 x 10-5 12.2

0.0015 0.10 1.36 x 10-5 11.8

The mass transfer coefficient obtained by

applying the second kinetic model is in the range of

0.10 – 0.28 cm/minute. This value is far greater than

the mass transfer coefficient obtained from the

application of the first kinetic model, which is in the

range of 8.38 x 10-5 - 1.97 x 10-4 cm/minute.

Meanwhile, the value of the effective diffusivity

tends to decrease from 2.13 x 10-5 cm2/minute to

5.52 x 10-6 cm2/minute when the solute

concentration increases from 75 ppm to 275 ppm and

it tends to increase from 6.54 x 10-6 cm2/minute to

1.36 x 10-5 cm2/minute when the ratio of the

adsorbent mass to the solution volume is increased

from 0.001 g/ml to 0.0015 g/ml.

When the second kinetic model was applied, the

absolute average deviation value is in the range of

4.1% -14.4%. It was much lower than its value when

the first kinetic model was applied, which was in the

range of 15.7% - 25.1%. This shows that, compared

to the first model, the second model is more suitable

for this case. Furthermore, these results also show that

in this case, the transfer of solutes into the particle is

controlled by the solute diffusion step within the

adsorbent particle. The determining factor for the

controlling stage is the pore structure of the particles.

The pore structure will determine the resistance of

solute diffusion within the particle.

3.3 Dyes Removal

The ability of adsorbent to absorb dyes is shown by

its removal value. Basically, the removal of the dye is

the mass of the dyes separated from the solution to the

initial mass of the dye.

The acid violet removal profile overtime at

various mass fractions of the adsorbent in the solution

when the initial solute concentration 275 ppm was

presented in Figure 3. The profile shows that up to 60

minutes, the percentage of dyes removal is still

increasing. This means that up to 60 minutes, the

adsorption process has not finished.

It can also be seen that the greater the ratio of the

mass of adsorbent to the volume of solution, the

greater the removal of the dyes. The highest removal

achieved was 58% when used 0.0015 g adsorbent per

ml solution.

Figure 3: Acid violet 17 removals at various ratio adsorbent

mass to solution volume, when the initial solute

concentration 275 ppm.

ICONIT 2019 - International Conference on Industrial Technology

134

4 CONCLUSIONS

Adsorption of acid violet 17 to activated carbon takes

place on a homogeneous solid surface form a single

layer at the surface. The maximum dyes removal

capacity is 185.19 mg/g. From the kinetic study, it

was known that the mechanism of acid violet 17

adsorptions on activated carbon is determined by the

diffusion stage in the particle. The percent dyes

removal was 58% achieved when 0.0015 g adsorbent

was used per ml solution.

ACKNOWLEDGMENTS

A deep gratitude is given to Stephanus Wibowo and

Andrew Riyadi S. for their full support during the

completion of this research works.

REFERENCES

Abd-Elhamid, A.I., Kamoun, E.A., El-Shanshory, A.A.,

Soliman, H.M.A. & Aly, H.F., 2019. Evaluation of

graphene oxide-activated carbon as effective composite

adsorbent toward the removal of cationic dyes:

Composite preparation, characterization and adsorption

parameters. Journal of Molecular Liquids 279, 530-539.

Belbel, B., Kharroubia, M., Janot, J., Abdessamad, M.,

Haouzi, A., Lefkaier, I.K. & Balme, S., 2018.

Preparation and characterization of homoionic

montmorillonite modified with ionic liquid:

Application in dye adsorption. Colloids and Surfaces A:

Physicochem. Eng. Aspects 558, 219-227.

Benabi, S., Streit, A.F.M., Benguerb, Y., Dotto, G.L., Erto,

A. & Ernst, B., 2019. Molecular modeling of anionic

and cationic dyes adsorption on sludge derived

activated carbon. Journal of Molecular Liquids 289, 1-

Boudechiche, N., Fares, M., Ouyahia, S., Yazid, H., Trari,

M. & Sadaoui, Z., 2019. Comparative study on removal

of two basic dyes in aqueous medium by adsorption

using activated carbon from Ziziphus lotus stones.

Microchemical Journal 146, 1010-1018.

Daoud, M., Benturki, O., Girods, P., Donnot, A. & Fontana,

S., 2019. Adsorption ability of activated carbons from

Phoenix dactylifera rachis and Ziziphus jujube stones

for the removal of commercial dye and the treatment of

dyestuff wastewater. Microchemical Journal 148, 493-

502.

Dotto, G.L., Buriol, C. & Pinto, L.A.A. (2014) Diffusional

mass transfer model for the adsorption of food dyes on

chitosan films. Chemical Engineering Research and

Design 92, 2324-2332.

Ferreira, Guilherme M.D., Ferreira, Gabriel M.D.,

Hespanhol, M.C., Rezende, J., Pires, A.C. , Gurgel,

L.V.A & Mendes da Silva, L.H., 2017. Adsorption of

red azo dyes on multi-walled carbon nanotubes and

activated carbon: A thermodynamic study. Colloids

and Surfaces A: Physicochem. Eng. Aspects 529, 531-

540.

Gamoudi, S. & Srasra, E., 2019. Adsorption of organic

dyes by HDPyþ-modified clay: Effect of molecular

structure on the adsorption. Journal of Molecular

Structure 1193, 522-531.

Gao, Y., Deng, S., Jin, X., Cai, S., Zheng, S. & Zhang, W.,

2019. The construction of amorphous metal-organic

cage-based solid for rapid dye adsorption and time-

dependent dye separation from water. Chemical

Engineering Journal 357, 129-139.

Goswami, M. & Phukan, P., 2017. Enhanced adsorption of

cationic dyes using sulfonic acid modified activated

carbon. Journal of Environmental Chemical

Engineering 5 (4), 3508-3517.

Herrera-González, A.M., Caldera-Villalobos, M. & Peláez-

Cid, A., 2019. Adsorption of textile dyes using an

activated carbon and crosslinked polyvinyl phosphonic

acid composite. Journal of Environmental Management

234, 237-244.

Jain, S.N. & Gogate, P.R., 2017. Adsorptive removal of

acid violet 17 dye from wastewater using biosorbent

obtained from NaOH and H2SO4 activation of fallen

leaves of Ficus racemosa. Journal of Molecular Liquids

243, 132–143.

Kausar, A., Iqbal, M., Javed, A., Aftab, K., Nazli, Z., Bhatti,

H.N. & Nouren, S. (2018) Dyes adsorption using clay

and modified clay: A review. Journal of Molecular

Liquids 256, 395-407.

Khorasani, A.C. & Shojaosadati, S.A., 2019. Magnetic

pectin-Chlorella vulgaris biosorbent for the adsorption

of dyes. Journal of Environmental Chemical

Engineering 7 (3), 1-8.

Liu, K., Deng, L., Li, H., Bao, Y., Xiao, Z., Li, B., Zhou,

Q., Geng, Y. & Wang, L., 2019. Two isostructural

Co/Ni fluorine-containing metal-organic frameworks

for dye adsorption and supercapacitor. Journal of Solid

State Chemistry 275, 1-7.

Li, W., Mu, B. & Yang, Y. (2019) Feasibility of industrial-

scale treatment of dye wastewater via bioadsorption

technology. Bioresource Technology 277, 157-170.

Magdy, Y.H. & Altaher, H., 2018. Kinetic analysis of the

adsorption of dyes from high strength wastewater on

cement kiln dust. Journal of Environmental Chemical

Engineering 6 (1), 834-841.

Ocampo-Perez, R., Leyva-Ramos, R., Alonso-Davila, P.,

Rivera-Utrilla, J. & Sanchez-Polo, M., 2010. Modeling

adsorption rate of pyridine onto granular activated

carbon. Chemical Engineering Journal 165, 133-141.

Ocampo-Perez, R., Leyva-Ramos, R., Mendoza-Barron, J.

& Guerrero-Coronado, R.M., 2011. Adsorption rate of

phenol from aqueous solution onto organobentonite:

Surface diffusion and kinetic models. Journal of

Colloid and Interface Science 364, 195-204.

Ocampo-Pérez, R., Rivera-Utrilla, J., Gómez-Pacheco, C.,

Sánchez-Polo, M. & López-Peñalver, J.J., 2012.

Kinetic study of tetracycline adsorption on sludge-

Mass Transfer Modeling of Acid Violet 17 Adsorption onto Activated Carbon

135

derived adsorbents in aqueous phase. Chemical

Engineering Journal 213, 88-96.

Rajabi, M., Mahanpoor, K. & Moradi, O., 2019.

Preparation of PMMA/GO and PMMA/GO-Fe3O4

nanocomposites for malachite green dye adsorption:

Kinetic and thermodynamic studies. Composites Part

B: Engineering 167, 544-555.

Saleem, M., Pirzada, T. & Qadeer, R., 2007. Sorption of

acid violet 17 and direct red 80 dyes on cotton fiber

from aqueous solutions. Colloids and Surfaces A:

Physicochem. Eng. Aspects 292, 246–250.

Thinakaran, N., Baskaralingam, P., Pulikesi, M.,

Panneerselvam, P. & Sivanesan, S., 2008. Removal of

Acid Violet 17 from aqueous solutions by adsorption

onto activated carbon prepared from sunflower seed

hull. Journal of Hazardous Materials 151, 316–322.

Vahdati-Khajeh, S., Zirak, M., Tejrag, R.Z., Fathi, A.,

Lamei, K. & Eftekhari-Sis, B., 2019. Biocompatible

magnetic N-rich activated carbon from egg white

biomass and sucrose: Preparation, characterization and

investigation of dye adsorption capacity from aqueous

solution. Surfaces and Interfaces 15, 157-165.

Yao, C. & Chen, T., 2018. A weighted average kinetic

equation and its application in estimating mass transfer

coefficients in liquid phase adsorption. Biophysical

Chemistry 241, 50-54.

Yu, Y., Qiao, N., Wang, D., Zhu, Q, Fu, F., Cao, R. Wang,

R., Liu, W. & Xu, B., 2019. Fluffy honeycomb-like

activated carbon from popcorn with high surface area

and well-developed porosity for ultra-high efficiency

adsorption of organic dyes. Bioresource Technology

285, 2-10.

ICONIT 2019 - International Conference on Industrial Technology

136