Comparative Economic between Bat Algorithm (Ba) and Particle

Swarm Optimization (Pso) for Solving Economy Dispatch

Vicky Andria Kusuma

, Restu Mukti Utomo

, Lucky Dwi Saputra

, Yuli Prasetyo

Institut Teknologi Kalimantan

Politeknik Negeri Balikpapan, Electrical Engineering, East Kalimantan, Indonesia

Keywords: Artificial Intelligent, Bat algorithm, Economy dispatch, Particle Swarm Optimization (PSO)

Abstract: Artificial intelligence is intelligence made using the program and added to a system to efficiently accomplish

human work. In this research utilizing an artificial intelligence that is the bat algorithm method to solve

economic dispatch problems in PT. PERTAMINA RU V BALIKPAPAN This study consists of determining

the configuration of the generation of power in eight generators and steam requirements, the efficiency of the

configuration produced. In the 10 MW load variation, the bat algorithm produces a generation cost of 195.88

tons / h while the algorithm The PSO generates 196.83 tons / h. This shows that the bat algorithm can obtain

a generation cost that is smaller than the PSO, whereas the convergent speed of the bat algorithm is faster than

the PSO algorithm, this is shown from the 865-iteration algorithm in the bat can converge whereas at PSO

requires iteration to 956. At 20 MW load variation the bat algorithm is better than the PSO algorithm in terms

of the generation cost value and the speed of this is shown from the bat algorithm generation value is 201.96

tons / h and the iteration speed is 669 while the large PSO algorithm generation is 203.23 tons / h and speed

the iteration is 976

1 INTRODUCTION

Electricity is an important component in the

household, industrial, and commercial activities.

Electricity is obtained from the activity of converting

primary energy, which is then converted through

generators (Kautsar and Nugroho, 2017). A generator

is an electrical device used to convert mechanical

energy into electrical energy. Companies like PT.

PERTAMINA RU V has its own generator to meet its

own electricity needs. Many things affect the amount

of electricity generation expenditure itself, one of

which is the operating costs of a generator or

generator. The operation of a generator or generator

is very dependent on fuel, so this can be a special

concern because some of the operating costs incurred

are for fuel purposes (Ilyas, 2010). Analysis of

optimal power is needed to be able to minimize the

cost of generation, commonly known as economic

dispatch. Economic dispatch is the distribution of the

load on generating units in the system optimally

economic at a certain system price (Ilyas, 2010). The

optimization algorithm is one method that can be

applied to solve economic dispatch problems. In the

previous research, a modified improve particle swarm

optimization algorithm was applied to the Java Bali

500kV thermal system generator. This method can

reduce generation costs by 4.64% (Ilyas, 2010).

Contraction factor-based particle Swarm

optimization is an algorithm used to solve problems

in the Java Bali 500kV thermal generator system.

This method can reduce the cost of the generation of

Rp 995,318,000.00 per hour (Kanata, 2013). The Bat

algorithm can provide accuracy using Naive Bayes as

its evaluator, which is quite promising at 98.29%

when compared to the Exhaustive Search and Genetic

Search methods, which respectively yield 82.97%

and 82.55% results (Pallavi, 2013). Economic

dispatch problems are experienced by various

companies that have their own generators. PT.

PERTAMINA RU V Balikpapan has the same

problem because of PT. PERTAMINA RU V

Balikpapan has a generator to operate refineries to be

able to process the products they process. These

problems form the background of this study. The

author implements the bat algorithm at PT.

272

Kusuma, V., Utomo, R., Saputra, L. and Prasetyo, Y.

Comparative Economic between Bat Algorithm (Ba) and Particle Swarm Optimization (Pso) for Solving Economy Dispatch.

DOI: 10.5220/0009490402720280

In Proceedings of the 1st International Conference on Industrial Technology (ICONIT 2019), pages 272-280

ISBN: 978-989-758-434-3

PERTAMINA RU V Balikpapan. The bat algorithm

was chosen because the bat algorithm is included in

the new algorithm method and based on previous

research the bat algorithm has a more optimal

optimization result, so it can produce more

economical costs (Kautsar, 2017) The bat algorithm

provides better performance when compared to some

other algorithms such as the algorithm Genetics,

Particle Swarm Optimization and Geometric Particle

Swarm Optimization (Ahmad, 2013) and based on

research in economic dispatch optimization problem

bat algorithm able to save 1,23% compare to actual

cost and 0.12% to firefly algorithm (Wulandhari et

al., 2018), that's the reason why bat a was chosen. The

target to be achieved by the author is the bat algorithm

can determine the configuration of the generator

power distribution PT. PERTAMINA RU V

Balikpapan, knowing the efficiency of the

configuration produced in terms of expenditure. The

results obtained will be compared using Particle

Swarm Optimization (PSO).

2 THEORETICAL BASIS

Work on this research requires information -

information that can help the process of doing

research well. This information is written in this

section. Information about the definition of economic

dispatch, bat algorithm, and particle swarm

optimization.

2.1 Economic Dispatch

The operation of a power plant is very dependent on

fuel because most of the operating costs incurred are

for fuel purposes. Therefore, saving fuel costs in a

small percentage can have a very large effect on

saving operating costs. To produce electricity in a

power system requires a way how to make the cost of

generator fuel consumption or operating costs of the

whole system as minimum as possible by determining

the combination of the output power of each

generating unit under the constraints of the demands

of the system load and the generation capability limit

of each generating unit. This method is known as the

Economic Dispatch (ED). A power system consisting

of various thermal generating units used to meet the

electricity needs to be carried out optimally and

economically among the generating units in order to

obtain a minimum overall generation cost (Dewa,

2016). The economic dispatch problem commonly

found in a thermal generation is determining the

power output of each power plant that can meet the

demand for power at a minimum cost while still

considering the limits of generator generation (Rajab

and Faharuddin, 2014). The following is modeling

used for economic dispatch problems.

()

Ct C P





(1)

()

ii iiiii

CP a bP cP 

(2)

Where:

Ct: = Large costs required in the form of rupiah

or steam consumption

N = Total generator available

CiPi = Generation cost from generator i (RP /

hour) or (Ton / hour)

ai, bi, ci = Coefficient of generator i

Pi = Large power generator (MW)

i: = Index of dispatchable units

2.2 Bat Algorithm

The bat algorithm is an algorithm that was introduced

by Xin-She Yang in 2010. The bat algorithm is found

based on modeling of the behavior of bats in nature.

Bats use echolocation or the ability to use waves to

determine distances and differences between food or

prey and obstacles; bats fly irregularly, taking into

account the speed, position, and frequency,

wavelength, and loudness to search for food. Bats can

adjust wavelengths automatically (Yang, 2010). The

bat algorithm can adjust the frequency (f) and

loudness (A) values when hunting for prey, and if the

bat encounters a close prey then the bat will increase

the pulse rate (r) so that the echolocation frequency

will increase while the loudness level will decrease to

prevent the prey from escaping self. The bat

algorithm has several parameters that are determined

based on the characteristics of the bat. These

parameters are written in equation 3 to equation 10.

min max min

()

ff f f







( 3)

()

tt t

ii i i

vv xxf





( 4)

1tt t

ii i







(5)

1tt







( 6)

(1 exp( ))

rr t







( 7)

min max min

()

ff f f







( 8)

()*(1, )

ref

lb ub lb rand population 

( 9)

(1, )

ref

v random population

(10)

Where:

fi = Bat frequency i.

β = Random numbers from 0 to 1.

Comparative Economic between Bat Algorithm (Ba) and Particle Swarm Optimization (Pso) for Solving Economy Dispatch

273

= Bat velocity i on t-iteration.

= Bat position i in the t-iteration.



= Bat loudness in the t-iteration.



= Bat pulse rate i on the t-iteration.

i = Index of bat members.

t = Index of iteration.

Table 1: Pseudocode bat algorithm

The equations found in Tables 3 to 10 are formed

in a program arrangement so that they can solve the

problem. The use of these equations will be discussed

in pseudocode. The bat algorithm pseudocode is in

Table 1.

2.3 Particle Swarm Optimization

PSO is a population-based optimization technique

developed by James Kennedy and Russ Eberhart in

1995, inspired by the behavior of flocks of birds or

fish. This method uses a set of particles that work

together, where each particle represents a candidate

solution to explore possible solutions to optimization

problems. Each particle is initialized randomly, and

then the particles are allowed to "fly." At each

optimization step, each particle will evaluate its

ability and the ability of the surrounding particles.

Each particle can store the solution that produces the

best capability as one of the best solution candidates

for all the particles around it.

(1)

11 2 2

()()

kkkkkkkk

id i d id id d id

v v c r Pbest x c r Gbest x



  

(11)

11kk

id id





(12)

Where:

= particle position i, dimension d on

iteration k

= random values between 0 and 1

,cc

= coefficient of repetition

Pbest

= the best local position of particle i, on

iteration

Gbest

= the best global position on particle i, on

Iteration

= particle velocity i, dimension d in

iteration k

Explanation of equations 11 and 12 is discussed

with the Pseudocode PSO method in table 2 (Yang,

2010).

Table 2: Pseudocode PSO

ICONIT 2019 - International Conference on Industrial Technology

274

3 APPLICATION OF THE

METHOD

The method used to conduct research in this journal

is to determine the cost function and determine the

maximum and minimum generator limits.

3.1 Minimum and Maximum

Generator Limits

PT PERTAMINA RU V BALIKPAPAN has eight

steam turbine generator (STG) generation systems,

with four generators in power plant 1 and 4 generators

in power plant 2.

Table 3: Minimum and maximum limit generator

Generator

Limit

Minimum

(MW)

Maximum

(MW)

Power Plant 2

Steam Turbine Generator 2.1 0 8

Steam Turbine Generator 2.2 0 8

Steam Turbine Generator 2.3 0 8

Steam Turbine Generator 2.4 0 8

Generator

Limit

Minimum

(MW)

Maximum

(MW)

Power Plant 1

Steam Turbine Generator 1.5 0 8

Steam Turbine Generator 1.6 0 8

Steam Turbine Generator 1.4 0 8

Steam Turbine Generator 1.3 0 8

Table 3 shows the maximum and minimum

generation limits for each generator. The following is

an example explanation of table 3.1 Steam turbine

generator 2.1 has a minimum generation limit of 0

MW or is considered not to be used, and the

maximum limit of generation is 8 MW, so a steam

turbine generator 2.1 may not be generated more than

8 MW.

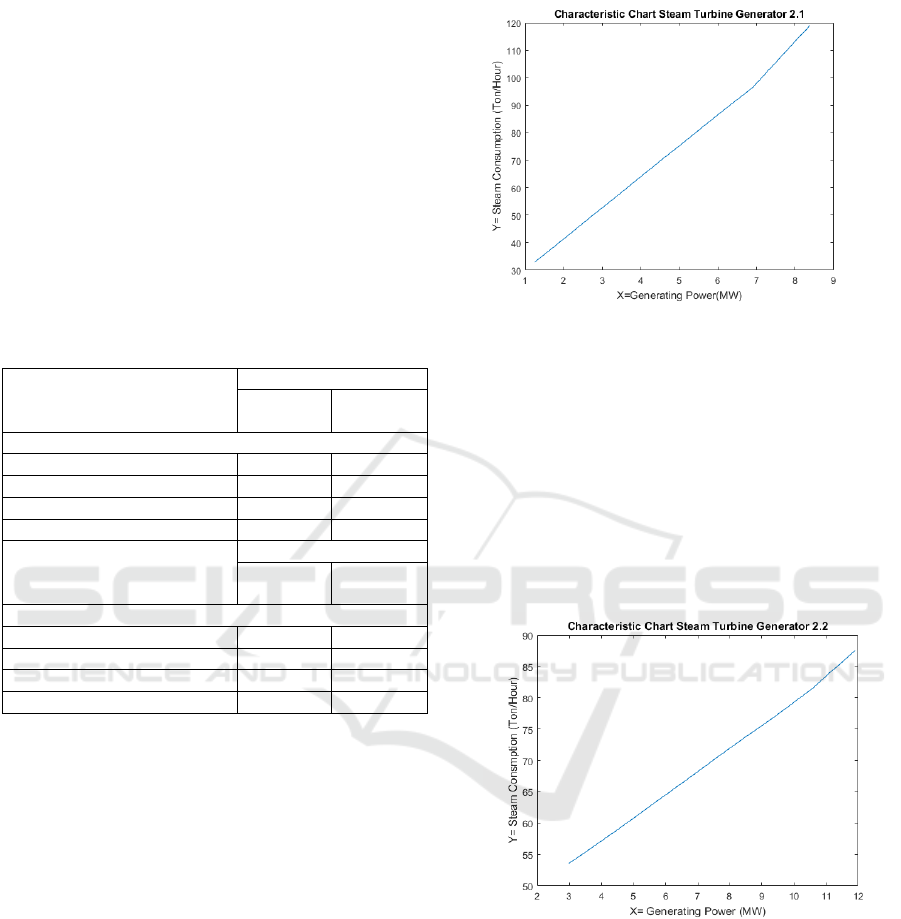
3.2 Cost Function STG 2.1

Figure 1 shows a graph of the ratio of power to steam

consumption in a steam turbine generator 2.1. From

the picture, we can take the following example for

STG 2.1, generating 3 MW of power. It takes 48.1-

tons of steam in one hour, whereas to generate 6 MW

of electricity requires 82.2-tons in one hour. The

formation of the cost function can be done using the

data in Figure 1, in equation 13 it is a form of the cost

function of Steam Turbine Generator 2.1.

0.24209 9.3967 21.838yxx

(13)

Figure 1: Characteristics STG 2.1

3.3 Cost Function STG 2.2

Figure 2 shows a graph of the ratio of power to steam

consumption in a steam turbine generator 2.2. It can

be seen that generating power starts from 3 MW and

requires the consumption of 43 tons in one hour while

generating 6 MW requires 63 tons in one hour. The

formation of the cost function on Steam Turbine

Generator 2.2 can be done using data 2. The results of

the cost function are in equation 14.

0.034 3.25 43.6yxx

(14)

Figure 2: Characteristics STG 2.2

3.4 Cost Function STG 2.3

Figure 3 shows the graph of the comparison of power

with steam consumption in a 2.3 2.3 steam turbine

generator. It can be seen that the generation power

starts from 3 MW and requires the consumption of 43

tons in one hour, whereas to generate 6 MW requires

63 tons in one hour in one hour, whereas to generate

6 MW requires 63-tons in one hour. The formation of

Comparative Economic between Bat Algorithm (Ba) and Particle Swarm Optimization (Pso) for Solving Economy Dispatch

275

the cost function on Steam Turbine Generator 2.2 can

be done using data 2. The results of the cost function

are in equation 15.

0.034 3.25 43.6yxx

(15)

Figure 3: Characteristics STG 2.3

3.5 Cost Function STG 2.4

Figure 4 shows a graph comparing the power with

steam consumption in a 2.4 steam turbine generator.

From the picture, we can take the following example

for STG 2.4 generating 3 MW of power required

steam of 19-tons in one hour. The cost function can

be done using the data in Figure 4, in equation 16, a

form of the cost function of Steam Turbine Generator

2.4.

0.047 4.6 4.3yxx

(16)

Figure 4: Characteristics STG 2.4

3.6 Cost Function STG 1.5

Based on Figure 5, the cost function of Steam Turbine

Generator 1.5 can be established. In equation 17 is the

result of forming a cost function from Steam Turbine

Generator 1.5.

0.17 11 51yxx





(17)

Figure 5: Characteristics STG 1.5

3.7 Cost Function STG 1.6

Based on Figure 6, the cost function of Steam

Turbine Generator 1.6 can be established. In

equation 18 is the result of forming a cost function

from Steam Turbine Generator 1.6.

0.16 4.7 6.1yxx  



(18)

Figure 6: Characteristics STG 1.6

3.8 Cost Function STG 1.4

Based on Figure 7, the cost function of Steam Turbine

Generator 1.4 can be established. In equation 19 is the

result of forming the cost function of Steam Turbine

Generator 1.4.

2.5 20 16yxx







(19)

ICONIT 2019 - International Conference on Industrial Technology

276



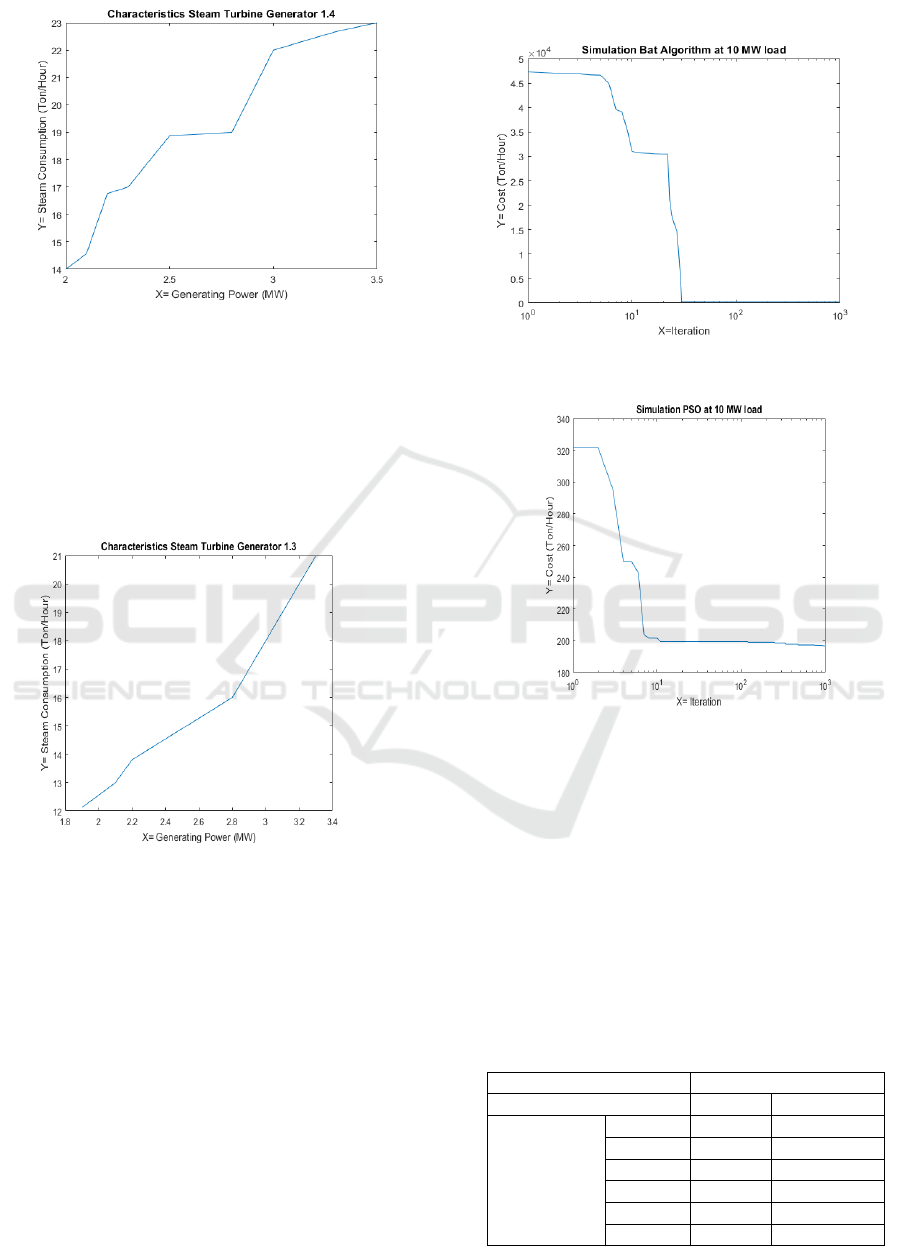
Figure 7: Characteristics STG 1.4

3.9 Cost Function STG 1.3

Based on Figure 8, the cost function of Steam Turbine

Generator 1.3 can be established. In equation 20 is the

result of forming the cost function of Steam Turbine

Generator 1.3.

3.1 10 21yxx



(20)

Figure 8: Characteristics STG 1.3

4 RESULT AND ANALYSIS

Economic dispatch simulation is performed using the

bat algorithm method and the PSO algorithm. The

simulation is carried out using MATLAB software.

4.1 Results of Simulations for 10 MW

Loads

Determination of the bat algorithm convergence

curve in solving economic dispatch is simulated with

1000 iterations, and the load requirement is 10 MW.

The convergence curve of the economic dispatch

problem is shown in Figure 9, while in Figure 10

shows the simulation results of the PSO algorithm.

Figure 9: The result of simulation bat algorithm at 10 MW

load

Figure 10 The result of simulation PSO at 10 MW load

Based on Figure 9, the bat algorithm can converge

at 865 iterations with a total expenditure of 195.88

Tons/hour. Figure 10 shows that the PSO algorithm

can converge at 956 iterations, while the generation

cost is 196.83 tons/hour. Based on the speed of the

algorithm to reach the convergence point, the bat

algorithm is better than the PSO algorithm and to

obtain the minimum expenditure costs obtained by

the bat algorithm with a difference of 0.95 Ton /

Hours. Table 4 shows the distribution of load on the

generator at a power requirement of 10 MW.

Table 4: Distribution load generator at 10 MW load

Load (MW) 10

Algorithm PSO BA

Load

distribution

(MW)

STG 2.1 0 0

STG 2.2 4,83 0,16

STG 2.3 1,48 7,61

STG 2.4 1,50 0,04

STG 1.5 0 0,01

STG 1.6 0 0

Comparative Economic between Bat Algorithm (Ba) and Particle Swarm Optimization (Pso) for Solving Economy Dispatch

277

STG 1.4 0 0

STG 1.3 2,20 2,18

Cost (ton/h) 196,83 195,88

Iteration 956 865

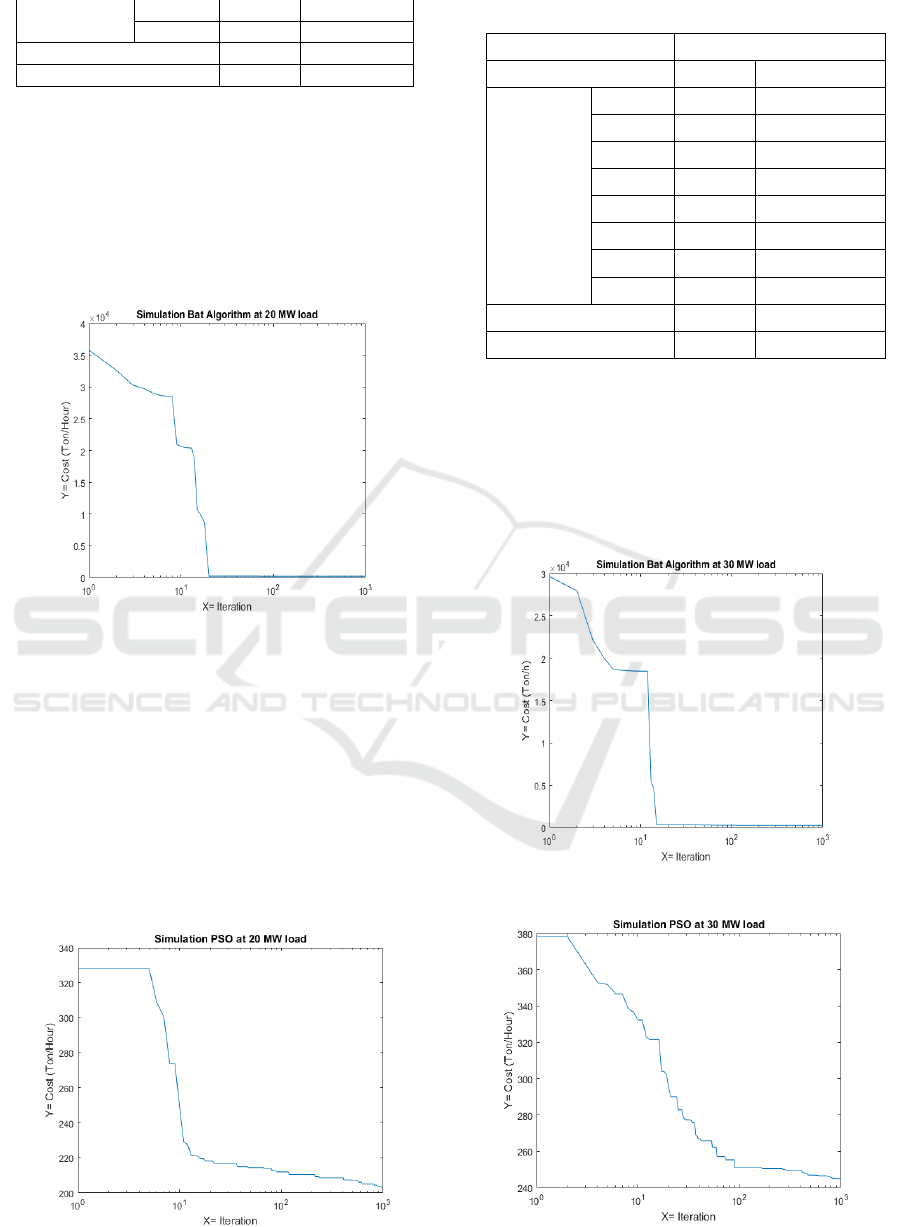
4.2 Results of Simulations for 20 MW

Loads

This simulation is carried out using a power

requirement of 20 MW. Figure 11 shows the

convergence curve of the bat algorithm at a load of 20

MW, while in Figure 12 shows the convergence curve

of the PSO algorithm.

Figure 11: The result of simulation Bat Algorithm (BA) at

20 MW load

Based on Figure 3, the bat algorithm convergence

curve is obtained at 669 iterations while the required

cost is 201.95 Tons / Hour. Figure 4 shows that PSO

can converge at 976 iterations with a cost of 203.23

ton/hour. By comparing the simulation results, it is

obtained that from the speed of the superior bat

algorithm with converging at 669 iterations while

PSO converges at 976 iterations. From the results

side, the bat algorithm is better than the PSO

algorithm. Table 5 shows the distribution of generator

power at a load of 20 MW.

Figure 12: The result of simulation PSO at 20 MW load

Table 5: Distribution load generator at 20 MW load

Load (MW) 20

Algorithm PSO BA

load

distribution

(MW)

STG 2.1

0 0

STG 2.2

4,00 4,66

STG 2.3

4,93 5,13

STG 2.4

0,38 0

STG 1.5

0 0

STG 1.6

0,50 0,01

STG 1.4

8,00 8

STG 1.3

2,20 2,20

Cost (ton/h)

203,23 201,96

Iteration

976 669

4.3 Results of Simulations for 30 MW

Loads

Figure 13 shows the results of the bat algorithm

simulation in the form of convergent curves, while in

Figure 14 shows the simulation results of the PSO

algorithm.

Figure 13: The result of simulation Bat algorithm at 30 MW

load

Figure 14: The result of simulation PSO at 30 MW load

ICONIT 2019 - International Conference on Industrial Technology

278

From Figure 13 and Figure 14, it can be seen that

in terms of speed, the bat algorithm is superior to the

PSO algorithm. Based on Figure 13, the bat algorithm

converges at 359 iterations. Figure 14 shows that the

PSO algorithm converges at 967 iterations. In terms

of the value generated, the bat algorithm is better than

the PSO algorithm. The value generated by the bat

algorithm is 242,765 Tons / Hour. In the PSO

algorithm, the resulting value is 244.98 Tons/hour.

From the two values, it can be seen that the results

issued by the bat algorithm are smaller. Table 6 shows

the distribution of generator power at a load of 30

MW.

Table 6: Distribution load generator at 30 MW load

Load (MW) 30

Algorithm PSO BA

load

distribution

(MW)

STG 2.1

0 0

STG 2.2

6,90 8

STG 2.3

7,30 8

STG 2.4

4,26 3,29

STG 1.5

0 0

STG 1.6

1,28 0,28

STG 1.4

8 8

STG 1.3

2,26 2,43

Cost (ton/h)

244,99 242,77

Iteration

967 359

4.4 Comparison of Algorithmic

Statistical Data

Statistical data consists of the best value, the worst

value, the average and the standard deviation of the

cost of expenditure by carrying out five times the data

collection with 1000 iterations and the load used is

32.7 MW. Statistical data is shown in table 7.

Table 7: Comperasion algorithm at statistic value

Algorithm

Best

value

(ton/h)

Worst

value

(ton/h)

Average

value

(ton/h)

STD

BAT 256,20 256,45 256,26 0,10

PSO 256,50 258,71 257,12 0,82

Based on statistical data in table 7, the minimum

cost (best value) is obtained by the bat algorithm

while the highest minimum cost (worst value) is

obtained by the PSO method, on average the bat

algorithm is superior compared to the PSO method

fixed at the standard deviation algorithm bat at 5

times of data retrieval the data difference is very small

at 0.09 while the PSO method is very large for data

differences in the data collection process that is equal

to 0.82 standard deviations the more the value is close

to zero then the better the program is made better.

5 CONCLUSIONS

Based on the results of experiments by comparing the

bat algorithm with the PSO algorithm. A comparison

of the two algorithms is made using three load

variations. The variations used are 10 MW, 20 MW,

and 30 MW. Statistical testing was carried out using

a load of 32.7 MW. In the 10 MW load variation the

bat algorithm produces a generation cost of 195.88

tons / h while the PSO algorithm generates 196.83

tons / h this shows that the bat algorithm can obtain a

generation cost that is less than the PSO, whereas at

the convergent convergence speed bats faster than the

PSO algorithm this is shown from the 865 iterations

to the bat algorithm can converge whereas the PSO

requires an iteration to 956. At 20 MW load variations

the bat algorithm is better than the PSO algorithm in

terms of the cost of generation and speed it is shown

from the value bat algorithm generation is 201.96 tons

/ h and iteration speed is 669 while the PSO algorithm

is 203.23 tons / h and iteration speed is 976. At 30

MW load variation, the bat algorithm is also better on

both sides. In the generation of 242.77 tons / h and for

iteration speed is 359. While in the PSO algorithm,

the generation rate is 244.99 tons / h, and the iteration

speed is 967. Based on the static test conducted by the

bat algorithm also obtained good values with STD of

0.1 while the PSO algorithm of 0.82.

REFERENCES

Ahmed Majid, Taha and Alicia Y.C. Tang. (2013) “Bat

Algorithm for Rough Set Attribute Reduction”. Journal

of Theoretical and Applied Information Technology,

Vol 51, No.1

Dewa, M., 2016. Perancangan Operasi Optimal Pembangkit

Listrik Tenaga Diesel (PLTD) dan Pembangkit Listrik

Tenaga Biogas (PLTBiogas) di Kabupaten Kepulauan

Meranti Menggunakan Metode Ekonomi Dispatch,

Jurnal Jom FTEKNIK, Volume 3, No 2

Ilyas, A., Penangsang, O., Soeprijanto, A., 2010.

Optimisasi Economic Dispatch Pembangkit Termal

Sistem 500 kV Jawa Bali Menggunakan Modified

Improved Particle Swarm Optimization, National

Conference: Design and Application of Technology,

Kanata, S., 2013. CFBPSO sebagai Solusi Economic

Dispatch pada Sistem Kelistrikan 500 kV Jawa-Bali,

Jurnal JNTETI, Vol 2, No 4

Comparative Economic between Bat Algorithm (Ba) and Particle Swarm Optimization (Pso) for Solving Economy Dispatch

279

Kim, S., 2016." A new metric of absolute percentage eror

for intermittent demand forecasts", International

Journal of Forecasting, Vol 32

Kautsar, F.M., Nugroho, A., 2017. Optimasi Ekonomis

Pembangkit PLTG di PLTGU Tambak Lorok

Menggunakan Algoritma Kelelawar, Jurnal Transient,

Vol 6, No 2.

Nugroho, A., 2006. Metode Pengaturan Penggunaan

Tenaga Listrik dalam Upaya Penghematan Bahan

Bakar Pembangkit dan Energi, Jurnal Transmisi, vol

11, No.1.

Rajab, A., Faharuddin, A., 2014. Pembagian Beban Secara

Ekonomis Pembangkit-Pembangkit Listrik Unit Termal

Menggunakan Kombinasi Metode Pemrograman

Dinamis dan Penyelesaian Secara Analitis, Artikel

Penelitian Dosen Muda, Vol 1

Syah, K., Dachlan, H.S., Hasanah, R.N., 2012. Analisis

Perbandingan Economic Dispatch Pembangkit

Menggunakan Metode Lagrange dan CFPSO, Jurnal

EECCIS, Vol 6, No.1.

Wulandhari, L.A., Komsiyah, S., Wicaksono, W., 2018. Bat

Algorithm Implementation on Economic Dispatch

Optimization Problem. Procedia Computer Science

135, 275–282.

https://doi.org/10.1016/j.procs.2018.08.175

Yang, X.-S., 2010. A New Metaheuristic Bat-Inspired

Algorithm, in: González, J.R., Pelta, D.A., Cruz, C.,

Terrazas, G., Krasnogor, N. (Eds.), Nature Inspired

Cooperative Strategies for Optimization (NICSO

2010). Springer Berlin Heidelberg, Berlin, Heidelberg,

pp. 65–74.

ICONIT 2019 - International Conference on Industrial Technology

280