
Multi-objective Modeling for a Course Timetabling Problem
Vertic Eridani Budi Darmawan
1
, Yuh Wen Chen
2
, Aisyah Larasati
1
, Deni Prastyo
1
and Anik
Dwiastuti
1
1
Department of Industrial Engineering, Universitas Negeri Malang, Malang, Indonesia
2
Institute of Industrial Engineering and Management, Da Yeh University, ChangHwa, Taiwan
Keywords:
University Timetabling, Curriculum-Based Course Timetabling, Multi-objective, Optimization.
Abstract:
This paper presents a multi-objective modelling approach for Curriculum Based Course Timetabling (CB-
CTT) problem. The problem comprises optimizing weekly scheduling by assigning offered courses to class-
rooms and time-periods. The model accommodates resource utilization of classroom occupation and the
limited cost by given two objective functions of minimizing loss cost of an empty seat and minimizing the
cost to open the course. The proposed model also satisfies the solutions that meet the lecturers time prefer-
ence, thereby produce the applied schedule for the lecturers. In terms of response time and quality, the model
outperformed manual alternatives to accommodate minimizing cost resources. The proposed model test using
private university data in Taiwan. The computational results are favourable and interactive using CPLEX 12.9
solver builds on AMPL.
1 INTRODUCTION
Producing an excellent educational timetabling is an
important issue and challenging task for every ad-
ministrative staff in an academic institution. It’s
needed hard work to fulfills the important stakeholder
(lecturers, students, and management) requirements.
Mostly, accommodating the new situation for the cur-
rent practice is to replicate the timetable in previous
years to speed up the process with some minor mod-
ification. However, recently, some changes may fre-
quently occur due to some new policy for each insti-
tution and mending of what has been developed pre-
viously take so much work. In these circumstances,
given the progress made in achieving the growth of
hardware and software systems, the scientific commu-
nity continues to investigate this issue in order to es-
tablish general and automated processes for establish-
ing effective and desirable timetables for stakeholders
(Bettinelli et al., 2015).
The curriculum-based course timetabling problem
defines as constructing the timetable by assigning the
university courses to the time-periods over the work-
ing days in a week and to the specific classroom that
suitable for the course need and the number of stu-
dents who registered the course and lecturer for each
courses in the weekly basis while satisfying various of
constraint (De Cesco et al., 2008). In every university,
the objective of producing a contented timetabling
could be a difference among others due to the dif-
ferences in preference and educational policy. How-
ever, the purpose is remaining the same to creates a
compelling and feasible timetabling by satisfying the
stakeholder’s preferences for at least to a certain ex-
tent (Kristiansen and Stidsen, 2013).
The curriculum-based course timetabling problem
has been explored extensively since 1980 by several
well-known techniques of the operational research
and the computer science field. In the last decade,
the primary methodologies use categorized as swarm
intelligence algorithm, evolutionary algorithm, lo-
cal search algorithm, graph coloring algorithm, and
the exact methods (Kristiansen and Stidsen, 2013).
Among those methodologies, the accurate methods,
integer programming, become one of the preferable
techniques that used in solving the problem to over-
come the quality of the solution found as the advance-
ment in computer software and hardware (Caccetta
and Aizam, 2012).
Clarence H. Martin (Martin, 2004) employed this
approach for Ohio University’s College of Busi-
ness by considering the practical issue on lecturers,
courses, classrooms, and timeslots. (Daskalaki et al.,
2004) perform a novel 0-1 integer programming for-
mulation by minimizing the linear cost function to
accommodate providing a significant number of op-
10
Budi Darmawan, V., Chen, Y., Larasati, A., Prastyo, D. and Dwiastuti, A.
Multi-objective Modeling for a Course Timetabling Problem.
DOI: 10.5220/0009857300100014
In Proceedings of the International Conference on Creative Economics, Tourism and Information Management (ICCETIM 2019) - Creativity and Innovation Developments for Global
Competitiveness and Sustainability, pages 10-14
ISBN: 978-989-758-451-0
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

erational rules and requirements for the constraints,
such as teaching periods, or days of week or class-
room specified courses using real data from Depart-
ment Electrical and Computer Science, University of
Patras. Lach and L
¨
ubbecke (Lach and L
¨
ubbecke,
2012) approaching the problem through integer lin-
ear programming using two stages decomposed tech-
nique using real data from the University of Udine,
Department Electrical and Computer Engineering.
The challenge in university course timetabling is
keeping the studied problem as close as to the prac-
tical problem as possible. The multi-objective opti-
mization does an influential part in this problem (Bet-
tinelli et al., 2015). In a weighted cost objective func-
tion to be minimized, a common strategy is to im-
plement constraints and penalize their violations. In
actual, some universities have some rule to consider
classroom capacity as the constraint that needs to ful-
fill (Bettinelli et al., 2015) as an approach in this study
to give a real contribution and theoretical in the re-
search community field. This paper organized as fol-
lows. The foundational problem of curriculum-based
course timetabling described. Then comes with the
explanation multi-objective model formulation, re-
sults, and discussion about the model performance
and conclusion.
2 PROPOSED APPROACH
This section describe the problem description of the
research area and the experimental design to construct
the problem.
2.1 Problem Description
In university curriculum-based course timetabling,
the problem formulated as given a set of course called
curriculum and each curriculum consists of several
lectures/courses. Each course is associated with a lec-
turer. Each course should be assigned in a classroom
at a time-period, which a time-period on particular
weekdays, without any conflicts. Each classroom also
has a specific size and requirement to accommodate
course needed. Fundamentally, to achieve an efficient
and feasible objective, the mathematical formulation
must be satisfied with all the related constraints. Ev-
ery institution has the policy to deal with its timetable,
so in many cases, adjustment much likely needed to
satisfying each timetabling community. In this pa-
per, the object of the study is a private university, Da-
Yeh University which located in ChangHwa, Taiwan.
Specifically, the data from the Industrial Engineering
and Management Department undergraduate course
in the College of Engineering with the time-period
of analysis is fall semester in the last two academic
years, 2017 and 2018. Figure 1 shows the collected
data.
Figure 1: Timetable Data.
In this paper, we assume and construct the time
preference for each professor for each semester as
close as a practical problem and accommodate the
classroom used for a particular equipped class, com-
puter class. The unique attributes university appears,
for the cost, every professor depends on the academic
status (assistant professor, associate professor, and
full professor) and the time-period (morning, after-
noon, and night). The higher academic standing, the
cost per hour, is higher. The time-period divides ev-
ery three hours length based on the length of course
offered, at morning, afternoon, and night. The night
time-period value is higher than the morning and af-
ternoon time-period. To satisfy the institution point of
view, the preference in having a good classroom oc-
cupancy due to efficiency resources, classroom, and
cost. Based on that, the model considering the funds
to satisfy the classroom capacity constraint and get
the feasibility timetabling.
2.2 Experimental Design
Constructing the university timetable using multi-
objective programming approach and the following
notation is needed to describe the model by given pa-
rameters that building the model as the essential struc-
tural element, the decision variables, objective func-
tion, and constraint. This model is a conceptual sim-
plified cost-minimizing model.
Parameters
c : course
r : classroom
t : time-period
s : student group
l : lecturer
fr : maximal capacity of classroom r
ec : number of students enrolled in course c
cost
c,r,t
: corresponding cost when the course c is as-
signed to classroom r, at period t
Il : set of course c taught by lecturer l
Is : set of course c attended by student group s
Tl : set of period t where the lecturer l is not available
Decision Variables
x
c,r,t
: boolean function, the value is 1 once the course
Multi-objective Modeling for a Course Timetabling Problem
11
c is assigned to a classroom r, at time-period t; other-
wise, it is zero.
Objective Function
A
1
= MinΣ
n
(c=1)
Σ
m
(r=1)
Σ
p
(t=1)
cost
(c,r,t)
x
(c,r,t)
( f
r
− e
c
)
(1)
Equation (1) is used to controlling the utilization
of classroom by minimizing loss cost for each empty
seat.
A
2
= MinΣ
n
(c=1)
Σ
m
(r=1)
Σ
p
(t=1)
cost
(c,r,t)
x
(c,r,t)
(2)
Equation (2) is used to design the timetabling by
minimizing cost. The mathematical formulation of
the problem is reads as follows:
Z = w
1
A
1
+ w
2
A
2
(3)
Constraint
Σ
m
(r=1)
Σ
p
(t=1)
X
(c,r,t)
= 1
1 ≤ c ≤ n (4)
Equation (4) indicates that each course must be
assigned in a classroom and at a period
Σ
n
(c=1)
x
(c,r,t)
≤ 1
1 ≤ r ≤ m, 1 ≤ t ≤ p (5)
Equation (5) indicates that each course cannot be
assigned to the same classroom and period, no colli-
sion.
e
c
x
(c,r,t)
≤ f
r
1 ≤ c ≤ n, 1 ≤ r ≤ m, 1 ≤ t ≤ p (6)
Equation (6) indicates the course capacity must be
satisfying classroom capacity.
Σ
n
(c∈I
l
)
nΣ
m
(r=1)
x
(c,r,t)
≤ 1
1 ≤ t ≤ p, 1 ≤ l ≤ L (7)
Equation (7) designates that each lecturer cannot
be assigned to more than one course in a given period,
no collision
Σ
n
(c∈I
l
)
Σ
m
(r=1)
Σ
p
(t∈T
l
)
x
(c,r,t)
= 0 (8)
Equation (8) indicates the courses timetable must
be satisfying the lecturer preference time.
Σ
n
(c∈I
s
)
Σ
m
(r=1)
x
(c,r,t)
≤ 1
1 ≤ t ≤ p, 1 ≤ s ≤ S (9)
Equation (9) designates that the student cannot be
assigned to more than one courses in a given period,
no collision.
The multi-objective framework considered for this
model, a weighted objective function is used to assist
the preference of decision maker to get a feasible so-
lution set (Hwang and Yoon, 1981). The subjective
weighted method use as simulated function to show
how each objective performs each other (Hwang and
Yoon, 1981).The model is designed to propose a sim-
ple input / output interface to integrate theory and user
practice (Chen, 2007).
3 RESULT AND DISCUSSION
Producing an excellent educational timetabling is an
important issue and challenging task for every admin-
istrative staff in an academic institution. It’s needed
hard work to fulfills the vital issue of stakeholder
(lecturers, students, and management) requirements.
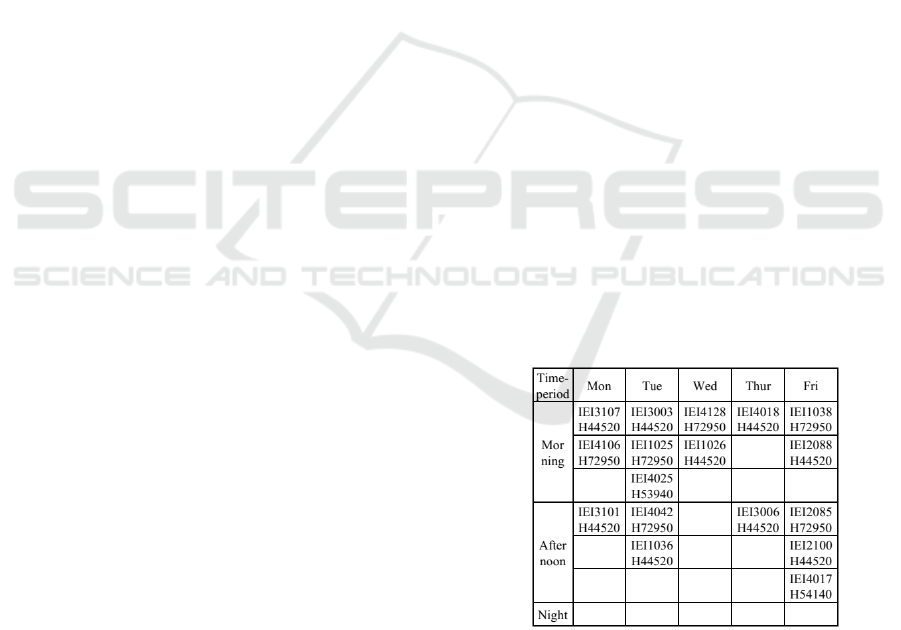
The result shows that timetable is favorably feasible,
shown in Figure 2 and Figure 3. The example of
computed timetable result applies 0.5 for each weight.
The suggested timetable shown the courses are held in
morning and afternoon time-period as a piece of ev-
idence how the model works that there is no courses
occur in the high-cost time-period.
Figure 2: Computed Timetable Academic Year 2018.
Figure 4 shows the variation value of Z in New
Taiwan Dollar (NTD) with the simulation weight be-
tween A1 and A2 (Steuer, 1986). A1 as the objective
to control the utilization of classroom to minimize the
loss cost of an empty seat. A2 as the objective to find
the feasible classroom, course and time-period that
minimize the cost. The weight represented as subject
ICCETIM 2019 - International Conference on Creative Economics, Tourism Information Management
12
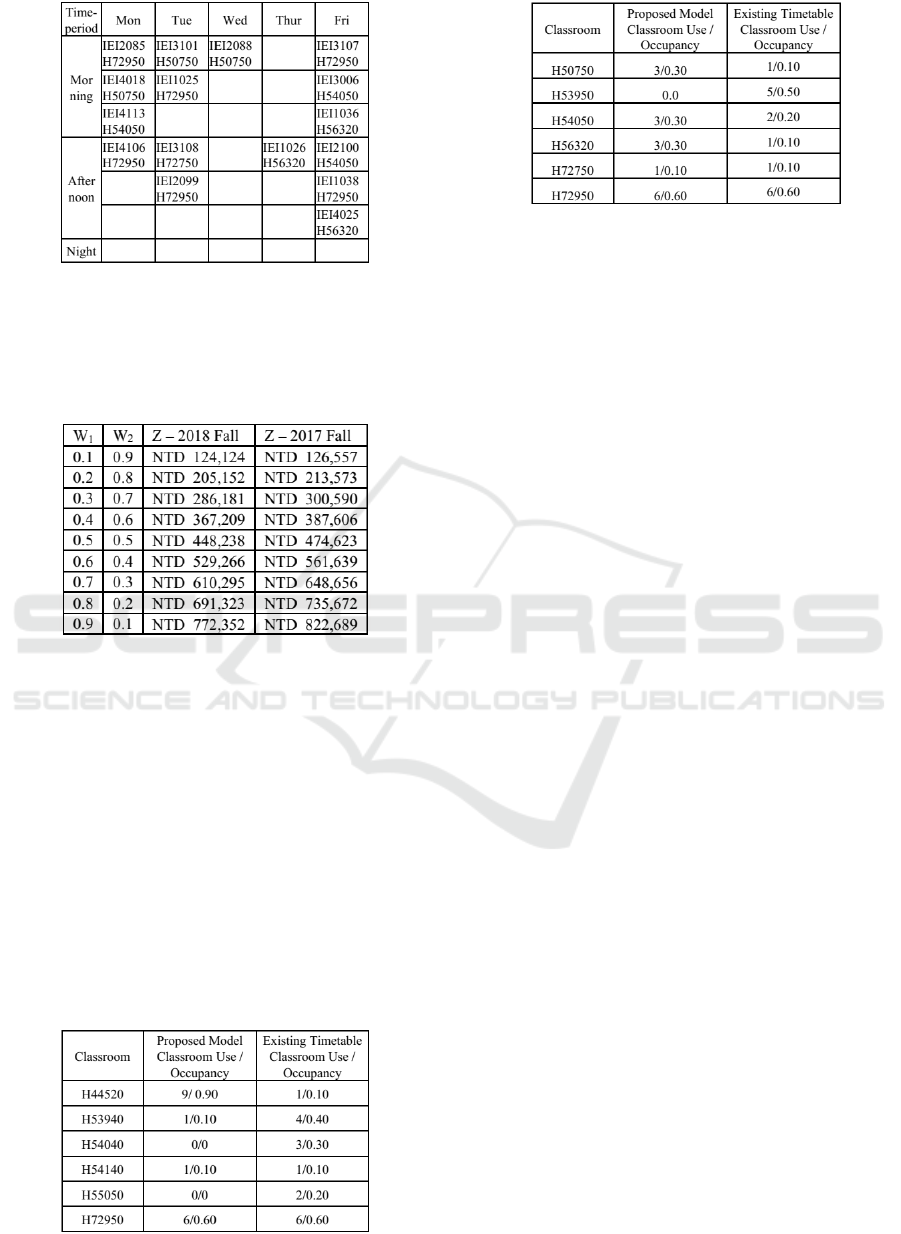
Figure 3: Computed Timetable Academic Year 2017.
preferences to the decision maker. The more domi-
nance penalty cost for the loss cost of an empty seat,
the cost result is getting higher.
Figure 4: Computed Result of Model Decision.
Comparing to the existing timetable, the total fund
that they need to spent to open the classroom for the
selected professor is identical. The difference is in
classroom occupancy operation; the proposed model
utilizes each classroom until reach maximum by min-
imizing loss cost of an empty seat for available class-
room and time-period for teacher except for particu-
lar equipped computer classroom, classroom H72950
and H72750, for the special equipment classroom for
special course. Meanwhile, the existing timetable
equalizes the classroom operation for each available
classroom within a time-period in the absence of the
empty seat consideration as shown in Figure 5 and
Figure 6.
Figure 5: Classroom Occupancy Academic Year 2018.
Figure 6: Classroom Occupancy Academic Year 2017.
4 CONCLUSIONS AND
RECOMMENDATIONS
Based on the results, the experimental work supports
that multi-objective programming is capable of gener-
ating the university course timetable. The developed
model considers the issue to satisfied the stakehold-
ers by minimizing the cost objective to accommodate
the university policy with favourable results within a
second compared to the manual process. The model
takes a penalty cost of an empty seat into considera-
tion as the way how this model can help to support the
decision maker giving broad options to optimize the
course timetable.
Interestingly, while most scholars are very famil-
iar with the concept, a few scholars consider cost in
the mathematical formulation to solve the problem
(Kristiansen and Stidsen, 2013). Since the finding
is simple, basic, and practical, this very beginning
conceptual simplified cost minimizing could be a ba-
sis for further model modification. The exploration
of weight assessment method lead to more develop-
ment in multi-objective modeling for future directions
(Chen, 2007).
ACKNOWLEDGEMENTS
This work is a joint research conducted by Universi-
tas Negeri Malang, Indonesia and Da Yeh University,
Taiwan and financially supported by the university re-
search fund (PNBP) 2019, the Institute of Research
and Community Services (LP2M), Universitas Negeri
Malang, Indonesia.
REFERENCES
Bettinelli, A., Cacchiani, V., Roberti, R., and Toth, P.
(2015). An overview of curriculum-based course
timetabling. Top, 23(2):313–349.
Multi-objective Modeling for a Course Timetabling Problem
13

Caccetta, L. and Aizam, N. A. H. (2012). Mixed integer lin-
ear programming models for university timetabling.
CONTRIBUTIONS IN MATHEMATICS AND APPLI-
CATIONS IV, page 90.
Chen, Y.-W. (2007). A group game of multiple attribute
decision making. Asia-Pacific Journal of Operational
Research, 24(05):631–645.
Daskalaki, S., Birbas, T., and Housos, E. (2004). An inte-
ger programming formulation for a case study in uni-
versity timetabling. European Journal of Operational
Research, 153(1):117–135.
De Cesco, F., Di Gaspero, L., and Schaerf, A. (2008).
Benchmarking curriculum-based course timetabling:
Formulations, data formats, instances, validation, and
results. In Proceedings of the seventh PATAT Confer-
ence, volume 2008.
Hwang, C.-L. and Yoon, K. (1981). Methods for multiple
attribute decision making. In Multiple attribute deci-
sion making, pages 58–191. Springer.
Kristiansen, S. and Stidsen, T. R. (2013). A comprehensive
study of educational timetabling-a survey.
Lach, G. and L
¨
ubbecke, M. E. (2012). Curriculum based
course timetabling: new solutions to udine bench-
mark instances. Annals of Operations Research,
194(1):255–272.
Martin, C. H. (2004). Ohio university’s college of business
uses integer programming to schedule classes. Inter-
faces, 34(6):460–465.
Steuer, R. E. (1986). Multiple criteria optimization. Theory,
computation and applications.
ICCETIM 2019 - International Conference on Creative Economics, Tourism Information Management
14
