Graphs with Partition Dimension 3 and Locating-chromatic
Number 4
Debi Oktia Haryeni
1
and Edy Tri Baskoro
2
1
Department of Mathematics, Faculty of Military Mathematics and Natural Science, The Republic of Indonesia Defense
University, IPSC Area, Sentul, Bogor 16810, Indonesia
2
Combinatorial Mathematics Research Group,
Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung Jl. Ganesa 10 Bandung 40132 Indonesia
Keywords: Graph, Tree, Partition Dimension, Locating-Chromatic Number, Cycle, Path.
Abstract
: The characterization study of all graphs with partition dimension either 2,𝑛 − 2,𝑛− 1 or 𝑛 has been
completely done. In the case of locating-chromatic numbers, the efforts in characterizing all graphs with
locating-chromatic number either 2,3, 𝑛 − 1 or 𝑛 have reached to complete results. In this paper we present
methods to obtain a family of graphs having partition dimension 3 or locating-chromatic number 4 by using
the previous known results.
1 INTRODUCTION
The concepts of partition dimension and locating-
chromatic number of connected graphs were
introduced by Chartrand et al. in (Chartrand et al.,
1998) and in (Chartrand et al., 2002), respectively.
The locating-chromatic number for graphs is a special
case of the partition dimension notion. In order to
generalize these two concepts, Haryeni et al. in
(Haryeni et al., 2017) enlarged the notion of the par-
tition dimension so that it can be applied also to dis-
connected graphs, and Welyyanti et al. in (Welyyanti
et al., 2014) enlarged the notion of locating-chromatic
number for disconnected graphs.
Let 𝐹=(𝑉,𝐸) be a (not necessarily connected)
graph and Π={𝑆

,𝑆

,…,𝑆

} be a partition of 𝑉(𝐹),
where 𝑆

is a partition class of Π for each 1≤ 𝑖≤
𝑘. If the distance 𝑑

(𝑣,𝑆

)<∞ for all 𝑣∈𝑉(𝐹)
and 𝑆

∈Π, then the representation 𝑟(𝑣|Π) of 𝑣 with
respect to Π is (𝑑

(𝑣,𝑆

),𝑑

(𝑣,𝑆

),…,𝑑

(𝑣,𝑆

)).
The partition Π is a resolving partition of F if every
two distinct vertices 𝑢,𝑣∈ 𝑉(𝐹) have distinct
representations with respect to Π, namely 𝑟
(
𝑢
|
Π
)
≠
𝑟(𝑣|Π). The partition dimension of 𝐹, denoted by
𝑝𝑑(𝐹) for a connected 𝐹 or by 𝑝𝑑𝑑(𝐹) for a
disconnected 𝐹, is the cardinality of a smallest
resolving partition of 𝐹. For a disconnected graph 𝐹,
if there is no a resolving partition of 𝐹, then
𝑝𝑑𝑑(𝐹)=∞. In addition, if the partition Π is
induced by a proper 𝑘−coloring 𝑐, then we define the
color code 𝑐

(𝑣) of a vertex 𝑣∈𝑉(𝐹) with
(𝑑

(𝑣,𝑆

),𝑑

(𝑣,𝑆

),…,𝑑

(𝑣,𝑆

)). If all vertices of
𝐹 have different color codes, then 𝑐 is a locating
coloring of 𝐹.
The locating-chromatic number of 𝐹, denoted by
𝜒

(𝐹) for a connected 𝐹 or by 𝜒

′(𝐹) for a
disconnected graph 𝐹, is the least integer 𝑘 such that
𝐹 admits a locating 𝑘−coloring. Otherwise, we say
that 𝜒


(
𝐹
)
=∞.
Chartrand et al. in (Chartrand et al., 2000)
characterized all connected graphs on 𝑛(≥3)
vertices having the partition dimension 2,𝑛, or 𝑛−1.
Tomescu in (Tomescu, 2008) showed that there are
only 23 connected graphs on 𝑛(≥9) vertices with the
partition dimension 𝑛−2. Further results of the
partition dimension of graphs for some graph
operations, namely corona product, Cartesian product
and strong product, can be observed in (Rodr´ıguez-
Velazquez et al., 2016; Yero et al., 2014; Yero et al.,
2010).
On the other hand, all connected graphs on 𝑛
vertices with locating-chromatic number 𝑛 or 𝑛−1
was characterized in (Chartrand et al., 2003). In the
same paper, they also gave conditions for graph 𝐹 on
𝑛(≥ 5) vertices with 𝜒

(
𝐹
)
≤𝑛−2. The
characterization of all graphs with locating-chromatic
number 3 can be seen in (Baskoro and Asmiati, 2013)
and (Asmiati and Baskoro, 2012).
14
Haryeni, D. and Baskoro, E.
Graphs with Partition Dimension 3 and Locating-chromatic Number 4.
DOI: 10.5220/0009876400002775
In Proceedings of the 1st International MIPAnet Conference on Science and Mathematics (IMC-SciMath 2019), pages 14-19
ISBN: 978-989-758-556-2
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In this paper, motivated by the results of the
characterization of all graphs with locating-chromatic
number 3, we present some method to extend those
graphs so that their partition dimension is equal to 3.
Furthermore, we show that these new graphs have
locating-chromatic number 4. We also construct some
classes of graphs by connecting some vertices in a
disjoint union of paths, so that the partition dimension
of these graphs remains equal to 3.
In order to present the results, we need additional
notions and some known results as follows. Let Π=
{𝑆

,𝑆

,…,𝑆

} be a resolving partition of 𝑉(𝐹). For
an integer 𝑘≥1, a vertex 𝑢∈𝑉(𝐹) is defined as
𝑘−distance vertex with respect to Π if 𝑑

(
𝑣,𝑆

)
=0
or 𝑘 for any 𝑆

∈Π . Note that in the locating-
chromatic number of 𝐹, the only possible value of 𝑘
is 1 and the vertex 𝑢 satisfies this condition is called
a dominant vertex.
Definition 1.1. (Haryeni et al., 2019) Let F be a
graph and 𝛱={𝑆

,𝑆

,…,𝑆

} be a minimum
resolving partition of 𝐹. Two distinct vertices 𝑝,𝑞∈
𝑉(𝐹) in 𝑆

for some 𝑖∈[1,𝑘] are called
independent vertices with respect to 𝛱 if there exist
two distinct integers, namely 𝑗 and 𝑙 which different
from 𝑖 , such that 𝑑

𝑝,𝑆

−𝑑

𝑞,𝑆

≠
𝑑

(
𝑝,𝑆

)
−𝑑

(
𝑞,𝑆

)
. Furthermore, if there exists a
minimum resolving partition of 𝐹 such that any two
vertices in the same class partition are independent,
then 𝐹 is called an independent graph. Otherwise, 𝐹
is a dependent graph.
Definition 1.2. (Haryeni et al., 2019) Let F be a
graph and 𝐵⊆𝑉(𝐹) where 𝐵=(𝑏

,𝑏

,…,𝑏

). We
denote F [
(
𝑏

,𝑏

,…,𝑏

)
;
(
𝑛

,𝑛

,…,𝑛

)
] as a hair
graph of 𝐹 with respect to 𝐵 which is obtained from
𝐹 by attaching a path 𝑃


with 𝑛

(≥ 2) vertices to a
root vertex 𝑏

, for all 𝑖∈[1,𝑘]. Furthermore, the set
of all hair graphs obtained from the graph 𝐹 is
denoted by 𝐻𝑎𝑖𝑟(𝐹).
Theorem 1.3. (Haryeni et al., 2019) Let 𝐹 be a graph
with a finite partition dimension. For any 𝐻∈
𝐻𝑎𝑖𝑟(𝐹), then
𝑝𝑑𝑑
(
𝐻
)
≤
𝑝𝑑𝑑
(
𝐹
)
, 𝑖𝑓 𝐹 𝑖𝑠 𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑒𝑛𝑡,
𝑝𝑑𝑑
(
𝐹
)
+1, 𝑖𝑓 𝐹 𝑖𝑠 𝑑𝑒𝑝𝑒𝑛𝑑𝑒𝑛𝑡.
Proposition 1.4. (Haryeni et al., 2019) For any 𝑛≥
3, a path 𝑃

is a dependent graph with any resolving
2-partition.
Theorem 1.5. (Haryeni et al., 2017) Let 𝐹 be a
disjoint union of 𝑚 paths with different lengths. If
𝑚=1, then 𝑝𝑑(𝐹)=2. Otherwise, 𝑝𝑑𝑑(𝐹)=3.
Corrollary 1.6. (Haryeni et al., 2017) If 𝐻∈
𝐻𝑎𝑖𝑟
(
𝑃

)
and 𝐻≇𝑃

for any 𝑛≥𝑚, then
𝑝𝑑
(
𝐻
)
=3.
2 TREES WITH PARTITION
DIMENSION 3 AND
LOCATING-CHROMATIC
NUMBER 4
Let 𝑇 be a tree with 3 dominant vertices 𝑥,𝑦 and
𝑧, and 𝑎𝑃

= (𝑎,𝑥,𝑢

,𝑢

,𝑢

,𝑢

= 𝑦,𝑣

,𝑣

,
…,𝑣

,𝑣

=𝑧,𝑏) be a path with 𝑟,𝑠 odd. If 𝑟,𝑠>
1, then define 𝑢
∗
=𝑢




, 𝑢
∗∗
=𝑢




, 𝑣
∗
=𝑣




, and
𝑣
∗∗
=𝑣




. Note that all internal vertices 𝑢

and 𝑣

of 𝑇 excluding 𝑢
∗
,𝑢
∗∗
,𝑣
∗
and 𝑣
∗∗
have degree 2. In
The following result, Baskoro and Asmiati (Baskoro
and Asmiati, 2013) characterized all trees with
locating-chromatic number 3.
Lemma 2.1. (Baskoro and Asmiati, 2013) In any tree
𝑇 with 𝜒

(
𝑇
)
=3, the color code of any vertex is
(𝑎

,𝑎

,𝑎

) where {𝑎

,𝑎

,𝑎

}={0,1,𝑘} for some
𝑘≥1.
Theorem 2.2. (Baskoro and Asmiati, 2013) Let 𝑇 be
a tree on 𝑛(≥ 3) vertices. The value 𝜒

(
𝑇
)
=3 iff 𝑇
is isomorphic to either 𝑃

,𝑃

,𝑆
,
,𝑆
,
, or any subtree
in Figure 1 containing a path 𝑎𝑃

.
Theorem 2.3. Let 𝐹 be a graph other than a path
with 𝜒

′
(
𝑇
)
=3. Then, 𝐹 is always independent.
Proof. Let 𝑐: 𝑉
(
𝐹
)
→{1,2,3} be any 3-coloring on
graph 𝐹. Let Π={𝑆

,𝑆

,𝑆

} be the partition of 𝐹
induced by 𝑐. We will show that any two vertices
𝑝,𝑞∈𝑆

for some 𝑎∈[1,3] are independent vertices
with respect to Π. If 𝑝 and 𝑞 are in different partition
classes, then certainly 𝑝 and 𝑞 are independent. Now
assume that 𝑝 and 𝑞 are in the same class, say 𝑝,𝑞∈
𝑆

. This implies that 𝑐

(
𝑥
)
=(0,𝑐

,𝑐

) and 𝑐

(
𝑦
)
=
(
0,𝑑

,𝑑

)
. By Lemma 2.1, then we have 𝑐

(
𝑥
)
=
(0,𝑐

,1) and 𝑐

(
𝑦
)
=
(
0,𝑑

,1
)
, or 𝑐

(
𝑥
)
=
(0,1,𝑐

) and 𝑐

(
𝑦
)
=
(
0,1,𝑑

)
, or 𝑐

(
𝑥
)
=(0,1,𝑐

)
and
𝑐

(
𝑦
)
=
(
0,𝑑

,1
)
, or 𝑐

(
𝑥
)
= (0,𝑐

,1) and
Graphs with Partition Dimension 3 and Locating-chromatic Number 4
15

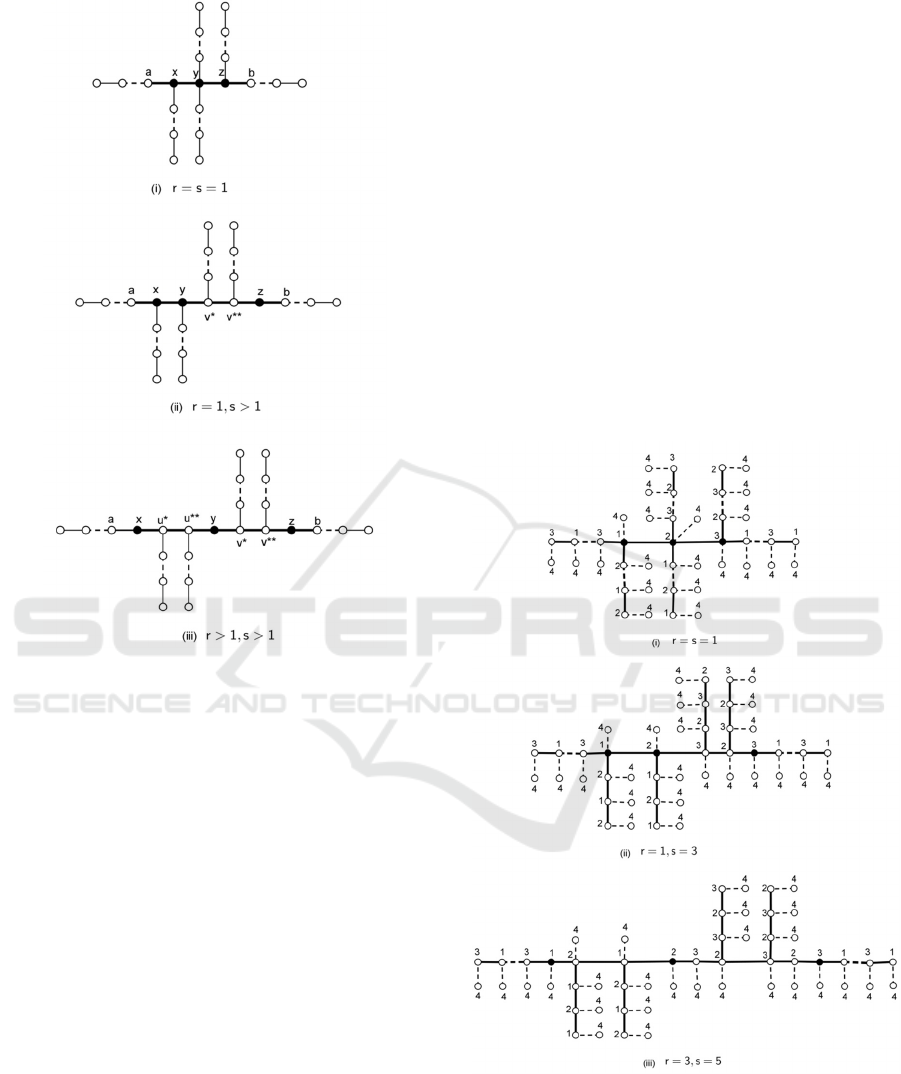
Figure 1: Any subtree 𝑇 containing a path 𝑎𝑃

with
𝜒

(
𝑇
)
=3 Now, we present the following results.
𝑐

(
𝑦
)
=
(
0,1,𝑑

)
. Note that 𝑐 is a locating coloring
of 𝐹 so that 𝑐

(
𝑥
)
≠𝑐

(
𝑦
)
. Therefore, for the
previous four cases we can conclude that 𝑐

−𝑑

≠
𝑐

−𝑑

. This implies that any two vertices 𝑥,𝑦 ∈ 𝑆

of 𝐹 are indepedent vertices so that 𝐹 is an
independent graph with respect to the partition Π.
By Theorems 2.2 and 2.3, we show that any hair
graph of tree 𝑇 in Theorem 2.2 has partition
dimension 3 and locating-chromatic number 4.
Corollary 2.4. Let 𝑇 be either a path 𝑃

or 𝑃

, a
double star 𝑆
,
or 𝑆
,
, or a subtree in Figure 1
containing a path 𝑎𝑃

. For all 𝐻∈𝐻𝑎𝑖𝑟(𝑇) where
𝐻≇𝑃

, then 𝑝𝑑(𝐻)=3 and with 𝜒

(𝐻)=4.
Proof. If 𝑇 is isomorphic to a path, then 𝑝𝑑
(
𝐻
)
=3
for any 𝐻∈𝐻𝑎𝑖𝑟(𝑇) with 𝐻≇𝑃

, by Corollary 1.5.
Now we suppose that 𝑇 is not isomorphic to a path.
Since 𝐻≇𝑃

, 𝑝𝑑(𝐻)≥3. By Theorems 2.2 and
2.3, then 𝑇 is an independent graph with locating 3-
coloring. By Theorem 1.3, then 𝑝𝑑(𝐻)≤𝑝𝑑(𝑇) ≤
𝜒

(𝑇)=3. Further-more, since all trees 𝑇 with
𝜒

(𝑇)=3 are only a path 𝑃

or 𝑃

, a double star
𝑆
,
or 𝑆
,
, or a subtree in Figure 1 containing a path
𝑎𝑃

, 𝜒

(
𝐻
)
≥4. The coloring of 𝐻 with 4 colors is
given in Figure 2. The color of the new vertices of 𝐻
are 4 and 𝑖 alternately, where 𝑖 is the color of the root
vertex.
3 GRAPHS CONTAINING CYCLE
WITH PARTITION
DIMENSION 3 AND
LOCATING-CHROMATIC
NUMBER 4
In the following theorem, all graphs containing cycle
with locating-chromating number 3 have been
characterized, see (Asmiati and Baskoro, 2012).
Figure 2: The locating 4-coloring of graph 𝐻∈𝐻𝑎𝑖𝑟(𝑇)
where 𝑇 depicted in Figure 1
Theorem 3.1. (Asmiati and Baskoro, 2012) Let 𝐹 be
any graph having a smallest odd cycle 𝐶. Then
𝜒

(𝐹)=3 iff 𝐹 is a subgraph of one of the graphs in
Figure 3 which every vertex 𝑎∉𝐶 of degree 3 must
IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)
16

be lie in a path connecting two different vertices in 𝐶.
By a similar reason to Corollary 2.4, we show that for
every 𝐻∈𝐻𝑎𝑖𝑟(𝐹), where 𝐹 is a graph in Theorem
3.1, then 𝑝𝑑(𝐻)=3 and 𝜒

(𝐻)=4.
Corollary 3.2. Let 𝐹 be any graph having a smallest
odd cycle 𝐶, where 𝐹 is a subgraph of one of the
graphs in Figure 3 which every vertex a 𝑎∉𝐶 of
degree 3 must be lie in a path connecting two different
vertices in 𝐶. For all 𝐻∈𝐻𝑎𝑖𝑟(𝐹), then 𝑝𝑑(𝐻)=3
and 𝜒

(𝐻)=4.
Figure 3: The four types of maximal graphs containing an
odd cycle with chromatic location number 3.
For now on, for any integer 𝑚≥2, define the graph
𝐺=
⋃
𝑃




where 𝑛

≥3 and 𝑛

= 𝑛

+1 for
all 𝑖∈[1,𝑚−1]. Note that 𝑝𝑑𝑑(𝐺)=3 by Lemma
1.5. In the next result, we construct some graphs
obtaining from disjoint union of paths 𝐺=
⋃
𝑃




so that their partition dimensions remains equal to 3.
Let the set of vertices and edges of 𝐺 by
𝑉
(
𝐺
)
=𝑣
,
:1≤𝑖≤𝑚,1≤𝑗≤𝑛

 and
𝐸
(
𝐺
)
=𝑣
,
𝑣
,
:1≤𝑖≤𝑚,1≤𝑗≤𝑛

−1,
respectively. Let 𝑆

,𝑆

and 𝑆

be three subsets of
𝑉(𝐺) where
𝑆

=𝑣
,
:1≤𝑖≤𝑚, (1)
𝑆

=𝑣
,
:1≤𝑖≤𝑚,2≤𝑗≤𝑖+1, (2)
𝑆

=𝑣
,
:1≤𝑖≤𝑚,𝑖+ 2≤𝑗≤𝑛

. (3)
By the above definitions, for three distinct vertices
𝑥,𝑦,𝑧∈ 𝑉(𝐹) where 𝑥=𝑣
,
∈𝑆

, 𝑦= 𝑣
,
∈ 𝑆

and 𝑧=𝑣
,
∈𝑆

for some 𝑖∈
[
1,𝑚
]
,𝑗∈[2,𝑖+ 1]
and 𝑘∈[𝑖 + 2,𝑛

], we have
𝑑

(
𝑥,𝑆

)
=
0, if 𝑡=1,
1, if 𝑡=2,
𝑖+ 1, if 𝑡=3,
𝑑

(
𝑦,𝑆

)
=
𝑗 − 1, if 𝑡=1,
0, if 𝑡=2,
𝑖+2−𝑗, if 𝑡=3,
𝑑

(
𝑧,𝑆

)
=
𝑘− 1, if 𝑡=1,
𝑘−𝑖−1, if 𝑡=2,
0, if 𝑡=3.
Now, define new graphs 𝐺

=𝐺∪𝐸

∪𝐸

and 𝐺⊆
𝐺

⊆𝐺′, where 𝐸

and 𝐸

are two sets of additional
edges connecting some vertices of 𝐹 as follows.
𝐸

=𝑣
,
𝑣
,
:1≤𝑖≤𝑚−1,1≤𝑗≤𝑛


𝐸

=𝑣
,
𝑣
,
:1≤𝑖≤𝑚−1,1≤𝑗≤𝑛

−1
By the above definitions, then 𝑉
(
𝐺

)
=𝑉
(
𝐺

)
=
𝑉
(
𝐺
)
. Let 𝑆

,𝑆

and 𝑆

be three subsets of 𝑉(𝐺’’)
similar to the equations in (1), (2) and (3),
respectively. Therefore, for three distinct vertices
𝑥,𝑦,𝑧∈ 𝑉(𝐺

) where 𝑥=𝑣
,
∈𝑆

, 𝑦=𝑣
,
∈𝑆

and 𝑧=𝑣
,
∈𝑆

where 𝑖∈
[
1,𝑚
]
, 𝑗∈[2,𝑖+ 1]
and 𝑘∈[𝑖+2,𝑛

], we have
𝑑


(
𝑥,𝑆

)
=min𝑑


𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑


𝑣
,
,𝑣
,

=𝑖+ 1,
𝑑


(
𝑦,𝑆

)
=min𝑑


𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑


𝑣
,
,𝑣
,

=𝑗− 1,
𝑑


(
𝑦,𝑆

)
=min𝑑


𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑


𝑣
,
,𝑣
,

=𝑖+ 2 − 𝑗,
𝑑


(
𝑧,𝑆

)
=min𝑑


𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑


𝑣
,
,𝑣
,

=𝑘− 1,
𝑑


(
𝑧,𝑆

)
=min𝑑


𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑


𝑣
,
,𝑣
,

=𝑘− 𝑖− 1.
Therefore, we obtain that
Graphs with Partition Dimension 3 and Locating-chromatic Number 4
17

𝑑


(
𝑥,𝑆

)
=
0, if 𝑡=1,
1, if 𝑡=2,
𝑖+ 1, if 𝑡=3,
𝑑


(
𝑦,𝑆

)
=
𝑗 − 1, if 𝑡=1,
0, if 𝑡=2,
𝑖+2−𝑗, if 𝑡=3,
𝑑


(
𝑧,𝑆

)
=
𝑘−1, if 𝑡=1,
𝑘−𝑖−1, if 𝑡=2,
0, if 𝑡=3.
By the above notations, we have the following results.
Theorem 3.3. Let 𝐺

=𝐺∪𝐸

∪𝐸

and 𝐺⊆𝐺

⊆
𝐺

. Then, 𝑝𝑑
(
𝐺

)
=3.
Proof. Since 𝐺’’ is not a path, 𝑝𝑑(𝐺’’)≥3. To show
the upper bound of partition dimension of 𝐺, define a
partition Π=
{
𝑆

,𝑆

,𝑆

}
of 𝐺′′ where 𝑆

=
𝑣
,
:1≤𝑖≤𝑚,𝑆

={𝑣
,
:1≤𝑖≤𝑚,2≤𝑗≤
𝑖+1}, and 𝑆

contains the rest vertices of 𝐺. By the
definition of partition Π, for a vertex 𝑣
,
∈𝑉(𝐺) in
𝑆

where 𝑖∈[1,𝑚], 𝑗∈[1,𝑛

] and 𝑎∈[1,3], we
have the representation of 𝑣
,
with respect to the
partition Π as follows.
𝑟𝑣
,
|Π
=
(0,1,𝑖+ 1), if 𝑗=1,
( 𝑗 − 1,0,𝑖 + 2 − 𝑗), if 𝑗∈
[
2,𝑖+ 1
]
,
( 𝑗 − 1,𝑗 − 𝑖− 1,0), if 𝑗∈
[
𝑖+2,𝑛

]
.
Let us show that Π is a resolving partition of 𝐺’’. We
consider any two vertices 𝑥,𝑦∈𝑉(𝐺’’). If 𝑥 and 𝑦are
in the different partition class, then clearly that they
have distinct representation. Now we suppose that
𝑥,𝑦 ∈ 𝑆

for some 𝑎∈[1,3]. If 𝑥=𝑣
,
and 𝑦=
𝑣
,
where 1≤𝑝≤𝑚 and 2≤𝑞<𝑟≤𝑝+
1 or 𝑝+2≤𝑞<𝑟≤𝑛

, then 𝑑


(
𝑥,𝑆

)
=𝑞−
1<𝑟−1=𝑑


(
𝑦,𝑆

)
. Therefore, 𝑟
(
𝑥
|
Π
)
≠
𝑟
(
𝑦
|
Π
)
.
Now, assume that 𝑥=𝑣
,
and 𝑦=𝑣
,
in 𝑆

for
some 𝑎∈
[
1,3
]
and 𝑝,𝑟∈[1,𝑚] where 𝑝≠𝑞. For
two vertices 𝑥=𝑣
,
and 𝑦=𝑣
,
in 𝑆

where 1≤
𝑝<𝑟≤𝑚, then 𝑑
’’
(𝑥,𝑆

)=𝑝+1<𝑟+1=
𝑑
’’
(𝑦,𝑆

). For two vertices 𝑥=𝑣
,
and 𝑦=𝑣
,
in
𝑆

where 1≤𝑝<𝑟≤𝑚,2≤𝑞≤𝑝+1 and 2≤
𝑠≤𝑟+1 , if 𝑑
’’
(𝑥,𝑆

)=𝑞−1=𝑠−1=
𝑑
’’
(𝑦,𝑆

) , then 𝑑
’’
(
𝑥,𝑆

)
=𝑝+2−𝑞<𝑟+2−
𝑠=𝑑
’’
(
𝑦,𝑆

)
.Otherwise, 𝑑
’’
(
𝑥,𝑆

)
≠𝑑
’’
(𝑦,𝑆

).
For two vertices 𝑥=𝑣
,
and 𝑦=𝑣
,
in 𝑆

where
1≤𝑝<𝑟≤𝑚,
𝑝+2≤𝑞≤𝑛

and 𝑟+2≤𝑠≤𝑛

, if 𝑑
’’
(
𝑥,𝑆

)
=
𝑞−1=𝑠−1=𝑑
’’
(
𝑦,𝑆

)
, then 𝑑
’’
(
𝑥,𝑆

)
=𝑞−
𝑝−1>𝑟−𝑠−1=𝑑
’’
(
𝑦,𝑆

)
. Otherwise,
𝑑
’’
(
𝑥,𝑆

)
≠𝑑
’’
(
𝑦,𝑆

)
. Therefore,
(
𝑥
|
Π
)
≠𝑟
(
𝑦
|
Π
)
for any two vertices 𝑥=𝑣
,
and 𝑦=𝑣
,
of 𝑉
(
𝐺

)
in 𝑆

for some 𝑎∈[1,3].
The four graphs in Figure 4 give an illustration of
the graphs provided for Theorem 3.3. These graphs
are (a) 𝐺=𝑃

∪𝑃

∪𝑃

∪𝑃

, (b) 𝐺′=𝐺∪ 𝐸

∪𝐸

,
(c) 𝐺


=𝐺∪𝐸

≅𝐺∪𝐸

and (d) 𝐺


⊂𝐺′. Note
that from Theorem 3.3, 𝑝𝑑(𝐺)=𝑝𝑑(𝐺′)=
𝑝𝑑(𝐺


)=𝑝𝑑(𝐺


)=3.
Figure 4: Graphs (a) 𝐺=𝑃

∪𝑃

∪𝑃

∪𝑃

, (b) 𝐺

=𝐺∪
𝐸

∪𝐸

, (c) 𝐺


=𝐺∪𝐸

, and (d) 𝐺


⊂𝐺

, where
𝑝𝑑(𝐺)=𝑝𝑑(𝐺′)=𝑝𝑑(𝐺


)=𝑝𝑑(𝐺


)=3.
In the next result, we also construct graphs from
disjoint union of paths 𝐺=
⋃
𝑃




, so that their
partition dimensions are equal to 3 as well.
Theorem 3.4. Let 𝐺

=𝐺∪𝐸

∪𝐸

,𝐹⊆𝐸(𝐺)
where 𝐹={𝑣
,
𝑣
,
:2≤𝑖≤𝑚−1,1≤𝑗≤𝑛

−
1} and 𝐹

⊆𝐹. Then, 𝑝𝑑
(
𝐺

−𝐹

)
=3.
Proof. Let 𝐻=𝐺

−𝐹′. This is easy to see that
𝑝𝑑(𝐻)≥3 . To show that 𝑝𝑑(𝐻)≤3 , define a
partition Π

={𝑆


,𝑆


,𝑆


} of 𝐻 where 𝑆


=𝑣
,
:1≤
𝑖≤𝑚,𝑆


={𝑣
,
:1≤𝑖≤𝑚,2≤𝑗≤𝑖+1} and
𝑆


=𝑣
,
:1≤𝑖≤𝑚,𝑖+2≤𝑗≤𝑛

.
By the definition of a partition Π′ of 𝑉(𝐻), for
three vertices 𝑥,𝑦,𝑧 ∈𝑉(𝐻) where 𝑥=𝑣
,
∈
𝑆


,𝑦=𝑣
,
∈𝑆


and 𝑧=𝑣
,
∈𝑆


for some 𝑖∈
[
2,𝑚
]
,𝑗∈[2, 𝑖 + 1] and 𝑘∈[𝑖 +2,𝑛

], we have
𝑑

(
𝑥,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑

𝑣
,
,𝑣
,

=1,
IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)
18

𝑑

(
𝑥,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑

𝑣
,
,𝑣
,

=𝑖+ 1,
𝑑

(
𝑦,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
= 
𝑑

𝑣
,
,𝑣
,
, if 𝑗≤𝑖,
𝑑

𝑣
,
,𝑣
,
, if 𝑗=𝑖+ 1.
= 
𝑗 − 1, if 𝑗≤𝑖,
𝑖, if 𝑗=𝑖+ 1.
=𝑗−1
𝑑

(
𝑦,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
= 
𝑑

𝑣
,
,𝑣
,
, if 𝑗=2,
𝑑

𝑣
,
,𝑣
,
, if 𝑗≠2.
= 
𝑖, if 𝑗=2,
𝑖−𝑗+2 if 𝑗≠2.
=𝑖+2−𝑗
𝑑

(
𝑧,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
=𝑑

𝑣
,
,𝑣
,

=𝑑

𝑣
,
,𝑣
,
+𝑑

(𝑣
,
,𝑣
,
)
=𝑘−1
𝑑

(
𝑧,𝑆


)
=min𝑑

𝑣
,
,𝑣
,
: 1≤𝑙≤𝑚
= 
𝑑

𝑣
,
,𝑣
,
, if 𝑘≤𝑚− 1,
𝑑

𝑣
,
,𝑣
,
, if 𝑘>𝑚−1.
= 
𝑘−1 − 𝑖, if 𝑘≤𝑚 − 1,
(
𝑚−𝑖
)
+(𝑘−𝑚−1) if 𝑘>𝑚−1.
=𝑘−1−𝑖.
.
By considering the resolving 3−partition Π=
{𝑆

,𝑆

,𝑆

} of a graph 𝐺′ in Theorem 3.3, we obtain
that for any vertex 𝑥∈𝑉(𝐺’) where 𝑉(𝐺’) = 𝑉(𝐻),
then 𝑟
(
𝑥
|
Π
)
=𝑟
(
𝑥
|
Π′
)
. Therefore, 𝑟
(
𝑥
|
Π′
)
≠
𝑟
(
𝑦
|
Π′
)
for any two vertices 𝑥,𝑦 ∈ 𝑉(𝐻) and so that
Π′ is a resolving partition of 𝐻.
Figure 5 represents some graphs satisfying
Theorem 3.4, namely (a) 𝐻=𝐺’−𝐹, (b) 𝐻

⊃𝐻
and (c) 𝐻

⊃𝐻 where 𝐻

=𝐺′−𝐹


and 𝐻

=𝐺′−
𝐹


for some 𝐹


,𝐹


⊆𝐹. Note that from Theorem 3.4,
𝑝𝑑(𝐻)=𝑝𝑑(𝐻


)=𝑝𝑑(𝐻


)=3.
Figure 5: Graphs (a) 𝐻=𝐺’−𝐹, (b) 𝐻

⊃𝐻 and (c) 𝐻

⊃
𝐻 where 𝐻

=𝐺′−𝐹


and 𝐻

=𝐺′−𝐹


for some
𝐹


,𝐹


⊆𝐹.
ACKNOWLEDGEMENTS
The second author thanks to the Ministry of Research
and Technology Indonesia for providing research
grant ”Penelitian Dasar Unggulan Perguruan Tinggi
(PDUPT)”.
REFERENCES
Asmiati and Baskoro, E. T. (2012). Characterizing all
graphs containing cycle with the locating-chromatic
number 3. AIP Conference Proceedings, 1450:351–
357.
Baskoro, E. T. and Asmiati (2013). Characterizing all trees
with locating-chromatic number 3. Electronic Journal
of Graph Theory and Applications, 1(2):109–117.
Chartrand, G., Erwin, D., Henning, M. A., Slater, P. J., and
Zhang, P. (2002). The locating-chromatics number of a
graph. Bulletin of the Institute of Combinatorics and its
Applications, 36:89–101.
Chartrand, G., Erwin, D., Henning, M. A., Slater, P. J., and
Zhang, P. (2003). Graph of order n with
locatingchromatics number n − 1. Discrete
Mathematics, 269:65–79.
Chartrand, G., Salehi, E., and Zhang, P. (1998). On the
partition dimension of a graph. Congressus
Numerantium, 130:157–168.
Chartrand, G., Salehi, E., and Zhang, P. (2000). The
partition dimension of a graph. Aequationes
Mathematicae, 59:45–54.
Haryeni, D. O., Baskoro, E. T., and Saputro, S. W. (2017).
On the partition dimension of disconnected graphs.
Journal of Mathematical and Fundamental Sciences,
49(1):18–32.
Haryeni, D. O., Baskoro, E. T., and Saputro, S. W. (2019).
A method to construct graphs with certain partition
dimension. Electronic Journal of Graph Theory and
Applications, 7(2):251–263.
Rodr´ıguez-Velazquez, J. A., Yero, I. G., and Kuziak, D. ´
(2016). The partition dimension of corona product
graphs. Ars Combinatoria, 127:387–399.
Tomescu, I. (2008). Discrepancies between metric
dimension and partition dimension of a connected
graph. Discrete Mathematics, 308:5026–5031.
Welyyanti, D., Baskoro, E. T., Simanjuntak, R., and
Uttunggadewa, S. (2014). The locating-chromatic
number of disconnected graphs. Far East Journal of
Mathematical Sciences, 94(2):169–182.
Yero, I. G., Jakovac, M., Kuziak, D., and Taranenko, A.
(2014). The partition dimension of strong product
graphs and cartesian product graphs. Discrete
Mathematics, 331:43–52.
Yero, I. G., Kuziak, D., and Rodr´ıguez-Velazquez, J. A. ´
(2010). A note on the partition dimension of cartesian
product graphs. Applied Mathematics and
Computation, 217:3571–3574.
Graphs with Partition Dimension 3 and Locating-chromatic Number 4
19