K-Means Clustering Optimization using the Elbow Method and Early

Centroid Determination Based-on Mean and Median

Edy Umargono

, Jadmiko Endro Suseno

and Vincensius Gunawan S. K.

Departement of Information System, Post Graduated School Diponegoro University, Jl. Imam Barjo, Semarang, Indonesia

Departement of Physics, Faculty of Science and Mathematics, Diponegoro University, Semarang, Indonesia

Keywords:

K-Means clustering, The Elbow Method, mean formula, median formula, centroid optimization.

Abstract:

The most widely used algorithm in the cluster partitioning method is the K-Means algorithm. Historically K-

Means is still the best grouping algorithm among other grouping algorithms with the ability to group a number

of data with relatively fast and efﬁcient computing time. The KMeans algorithm is widely implemented in

various ﬁelds in industrial and scientiﬁc applications and is very suitable for processing quantitative data with

numeric attributes but there are still weaknesses in this algorithm. Weaknesses of the K-Means algorithm

include determining the number of clusters based on assumptions and relying heavily on initial selection of

centroids to overcome this weakness, in this study, we propose the use of the elbow method to determine the

best number of clusters and determination of centroid based-on mean and median data. The results of this study

indicate that using initial centroid determination based on mean data makes the number of iterations needed to

achieve uniformity in clusters 22.58% less than using initial random cluster determination and determining the

best number of clusters using the elbow method makes the required iteration 25% less than using the number

of other clusters.

1 INTRODUCTION

Clustering is a process of grouping a set of data in a

dataset by dividing data into groups or clusters with

the principle of maximizing the high similarity in in-

traclass and minimizing the similarity in interclass

so that objects in one cluster have high similarity

but are very different from objects in other clusters

(Han et al., 2011) . Attribute values that describe

objects are used to assess dissimilarity and similar-

ity and usually involve distance measurements (Li

and Wu, 2012). The cluster method can generally be

classiﬁed as a partition method with mean or medoid

values that represent the cluster centroid values with

one level of grouping, hierarchical method with sev-

eral levels of grouping, density-based method, grid-

based method to handle spatial data. Judging from the

characteristics, ease of implementation and computa-

tional performance for grouping small and medium

data partition method with the average (mean) is the

most effective and efﬁcient (Wilks, 2011) .The data

to be grouped in this study are relatively small and of

medium-size so the partitionbased clustering method

using the mean is the most suitable method used in

this study.

The most widely used algorithm in the partition

method is the K-Means algorithm, K-Means is an it-

eration algorithm where the user determines the num-

ber of clusters to be used in grouping datasets and

determining the centroid for each cluster (Simovici

and Djeraba, 2014) so that the level the similarity

between members in one cluster is high whereas the

level of similarity with members in other clusters is

very low (Shakeel et al., 2018). Historically K-Means

is still the best clustering algorithm among other clus-

tering algorithms with the ability to group a number

of data with relatively fast and efﬁcient computing

time (L

opez-Rubio et al., 2018), (Bholowalia and Ku-

mar, 2014), (Kodinariya and Makwana, 2013)) and

become one of the most important algorithms in data

mining. KMeans algorithm is widely implemented in

various ﬁelds in industrial and scientiﬁc applications

(Shakeel et al., 2018) and is very suitable for process-

ing quantitative data with numerical attributes, how-

ever there are still weaknesses in this algorithm.

The weaknesses of the K-Means algorithm in-

clude the determination of the number of clusters

based on assumptions and relying heavily on the ini-

tial selection of cluster center (centroid) to overcome

these weaknesses, it is necessary to optimize, one of

234

Umargono, E., Suseno, J. and S. K., V.

K-Means Clustering Optimization using the Elbow Method and Early Centroid Determination Based-on Mean and Median.

DOI: 10.5220/0009908402340240

In Proceedings of the International Conferences on Information System and Technology (CONRIST 2019), pages 234-240

ISBN: 978-989-758-453-4

the popular cluster optimization methods is the El-

bow method (L

opez-Rubio et al., 2018) (Bholowalia

and Kumar, 2014), (Kodinariya and Makwana, 2013)

, (Liu et al., 2018). The Elbow method is a visual

method to test the consistency of the best number of

clusters by comparing the difference of the sum of

square error (SSE) of each cluster, the most extreme

difference forming the angle of the elbow shows the

best cluster number. In some of these studies, the fo-

cus is still on optimizing the determination of the best

number of clusters by the Elbow method while the

initial selection of centroid is still random. This al-

lows the number of iterations to place objects in the

cluster based on the center of the new cluster to be

more numerous so that the achievement of similarity

of patterns formed becomes longer.

Much research has been done related to determin-

ing the centroid value to improve the performance of

the K-Means algorithm including the idea of weight-

ing on each cluster variant as min-max K-Means

(Tzortzis and Likas, 2014), there are also studies with

a simple formula through weighting the highest and

lowest averages to be used as a centroid value (Fab-

regas et al., 2017) with better computational perfor-

mance results than the original K-Means, in this study

proposes the use of simple statistical mean and me-

dian formulas in initial determination of the centroid

and combined with the method Elbow to determine

the number of clusters used so that the performance

of the K-Means algorithm is better in terms of the

number of iterations needed and the consistency of

the generated cluster members compared to the origi-

nal K-Means method.

The K-means clustering algorithm in this research

will be implemented in the case study of mapping

data of teaching staff in public schools in districts,

cities in province of Central Java, with this grouping it

can be seen which schools have excess teaching staff

or lack of teaching staff so that they can be used as

a basis for distribution teaching staff as an effort to

equalize teaching staff placement in public schools in

Central Java so that there are no problems with ex-

cess or lack of teaching staff, excessive concentration

of teaching staff in certain areas, and aging teaching

staff population in placement in major city centers be-

cause of the distribution of teaching staff which is un-

even (Szelkagowska-Rudzka, 2018). In this study, it

is assumed that three main groups are formed that rep-

resent deﬁciency, sufﬁcient and excess conditions, to

improve the performance of the KMeans algorithm in

this study using the elbow method to evaluate the de-

termination of the best number of clusters and com-

bined with determining the initial centroid by compar-

ing the minimum value, the median value , the mean

value and maximum object values of the results of

the comparison of this experiment are used as a de-

terminant of the initial centroid, so it is expected to

reduce the number of iterations to achieve similarity

in the formed cluster rather than using the initial ran-

dom centroid determination.

2 MATERIALS AND METHODS

2.1 Materials

The data used in this study is a sample recapitulation

of Public high school data in Central Java Province

covering 16 of Public Senior High School data in Se-

marang City, 11 of Public Senior High School data

in Semarang Regency and 3 of Public Senior High

School data in Salatiga City and its attributes in-

cluding the name of the school, number of students

(ns), number of teachers (nt), number of study groups

(nsg), number of subjects (nsbc), data obtained from

http: //sekolah.data.kemdikbud.go.id and the Ofﬁce

of Education and Culture of the Central Java Provin-

cial Government, the data is downloaded in the form

of CSV ﬁle.

The tools used in this study are a set of computers

with AMD Dual Core A9-9420 3.6 GHz CPU hard-

ware speciﬁcations, 4GB RAM with Windows 10 op-

erating system, Excel applications, Orange Data Min-

ing, Python programming and Visual Studio Code ed-

itors as supporting software

2.2 Methods

In this study conducted using the following stages, the

ﬁrst stage is problem analysis at this stage a problem

analysis is carried out in the case study of equal dis-

tribution of teaching staff, especially in public schools

in districts, cities in Central Java, which results in the

formulation of the problem needed by mapping the

teaching staff in public schools.

The second stage is literature review, at this stage

a literature study method is conducted which will be

used to clustering data on existing case studies, the re-

sult of this stage is the use of the K-Means clustering

method for grouping data that enables improved per-

formance by determining the best number of clusters

and determining the initial centroid.

The third stage is data collection, the data used

are secondary data obtained from the website of

the Ministry of Education and Culture of the Re-

public of Indonesia at the address http: //seko-

lah.data.kemdikbud.go.id and other data from the

Ofﬁce of Education and Culture of Central Java

K-Means Clustering Optimization using the Elbow Method and Early Centroid Determination Based-on Mean and Median

235

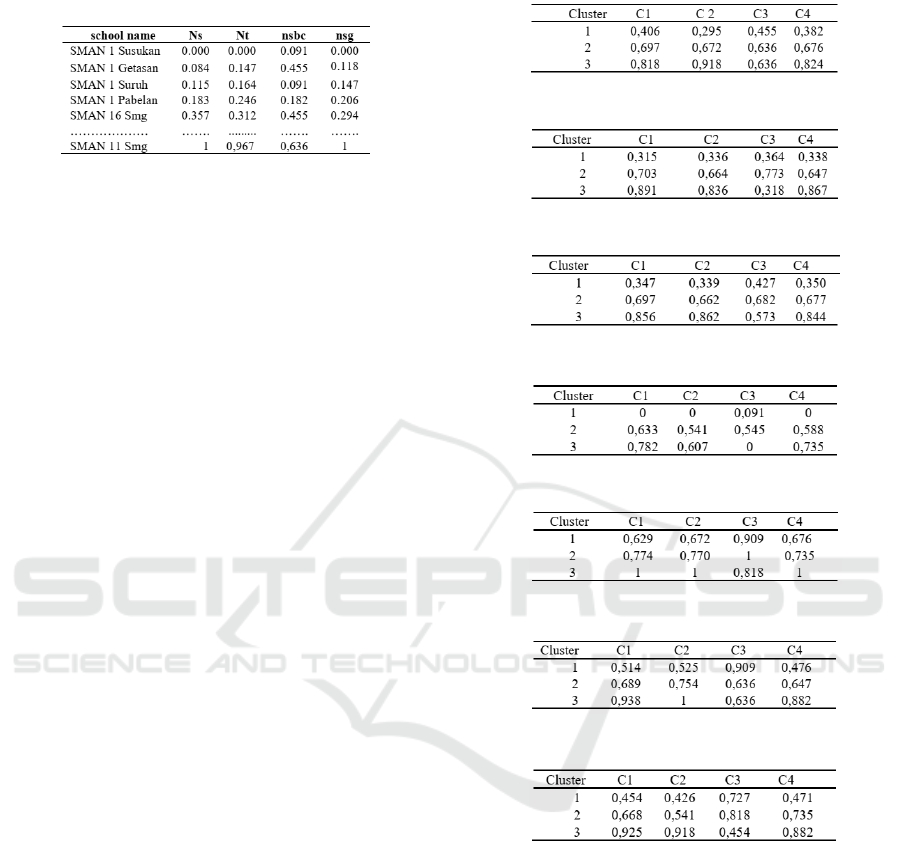
Province. Data attribute relationships are determined

with the Pearson Correlation Coefﬁcient are shown in

the Figure 1

Figure 1: Pearson Correlation Coefﬁcient (Schober et al.,

2018).

The fourth stage is data preparation, at this stage,

data cleaning is done from inconsistent data, incom-

plete data and then integrating data from different

sources, to eliminate attribute dominance, normaliza-

tion using the min-max method which places data in

the range of 0 as a minimum value up to 1 as a max-

imum value. With the following formula (Jain et al.,

2018).

X∗ =

x − minValue

maxValue − minValue

(1)

with x is the value to be normalized.

The ﬁfth stage is modeling, at this stage using the

K-Means algorithm to group data into a number of

groups that have been determined. K-Means Cluster-

ing is a prototype based clustering method where the

dataset is divided into a number of (k) - clusters, in

this method the user determines the number of clus-

ters (k) to be used. The purpose of KMeans Cluster-

ing is to ﬁnd a prototype for each cluster, all data ob-

jects are then assigned to the nearest prototype, which

then forms a cluster. The prototype is called centroid,

the center of the cluster. Centroid is the average of

all data objects in a cluster or the most representative

data object. K-Means clustering creates partitions (k)

in n-dimensional space, where n is the number of at-

tributes in the dataset. To partition data, proximity

measurements must be determined. The most com-

monly used measure for numerical attributes is the

Euclidean distance. Following are the stages of the

K-Means Clustering process (Simovici and Djeraba,

2014)

1. Determining the number of clusters by the user

2. Centroid initialization

The ﬁrst step in the k-means algorithm after deter-

mining the number of clusters is to start randomly

determining centroids. In this study it is proposed

to use the mean formula as a description of the av-

erage value of the cluster members shown in for-

mula (Sarkar and Rashid, 2016)

+ x

+ ... + x

(2)

with xj is object value in cluster and j number of

objects in cluster, and the formula for the single

data median as follows (Sarkar and Rashid, 2016),

if the data is odd and n is the amount of data then

the medians formula becomes

ME = X

n+1

(3)

If the amount of data is even then the median for-

mula becomes

ME =

(

)

+ x

(

+1)

) (4)

Median data by dividing the smallest and largest

addition values by formula

X∗ =

smallestvalue − largestvalue

(5)

3. Data allocation

Every data or object will be located to the clos-

est cluster. The distance between the two ob-

jects determines the proximity of the object. Dis-

tance measurement with Euclidean distance is

the most commonly used proximity measure, al-

though other measurements such as Manhattan

size and Jaccard coefﬁcient can be used. The Eu-

clidean distance (d) between two data points x

(x1, x2, ... xn) and c (c1, c2, ..., cn) with n at-

tributes is described in the Euclidean Distance for-

mula as follows (Draisma et al., 2016)

d =

(x1 − c1)2 + (x 2 − c2)

+ .. + (xn − cn)

(6)

with d is the distance of points x and c, xn is the

criterion data and cn is the centroid of the nth clus-

ter.

4. Calculate the new centroid

For each cluster, after the ﬁrst iteration data al-

location stage is completed then a new centroid

is calculated for the next iteration data allocation.

This new centroid is the most representative data

point of all data points in the cluster obtained from

the cluster average. Mathematically, this step can

be expressed as minimizing the sum squared er-

rors (SSE) from all data points in a cluster to the

centroid cluster. The overall goal of this step is

to minimize the SSE of each group. Here is the

new centroid determination formula(Sarkar and

Rashid, 2016)

x∈C

X (7)

CONRIST 2019 - International Conferences on Information System and Technology

236

with µ

is center point (centroid), X is object in the

cluster, ji the number of objects in the cluster.

5. Termination

The step of calculating a new centroid, and the

step to assign data points to the new centroid are

repeated until no more changes in the assignment

of data points occur. In other words, no signiﬁcant

changes in centroids were noted. The ﬁnal cen-

troid is declared as a prototype cluster and is used

to describe the whole grouping model. The stages

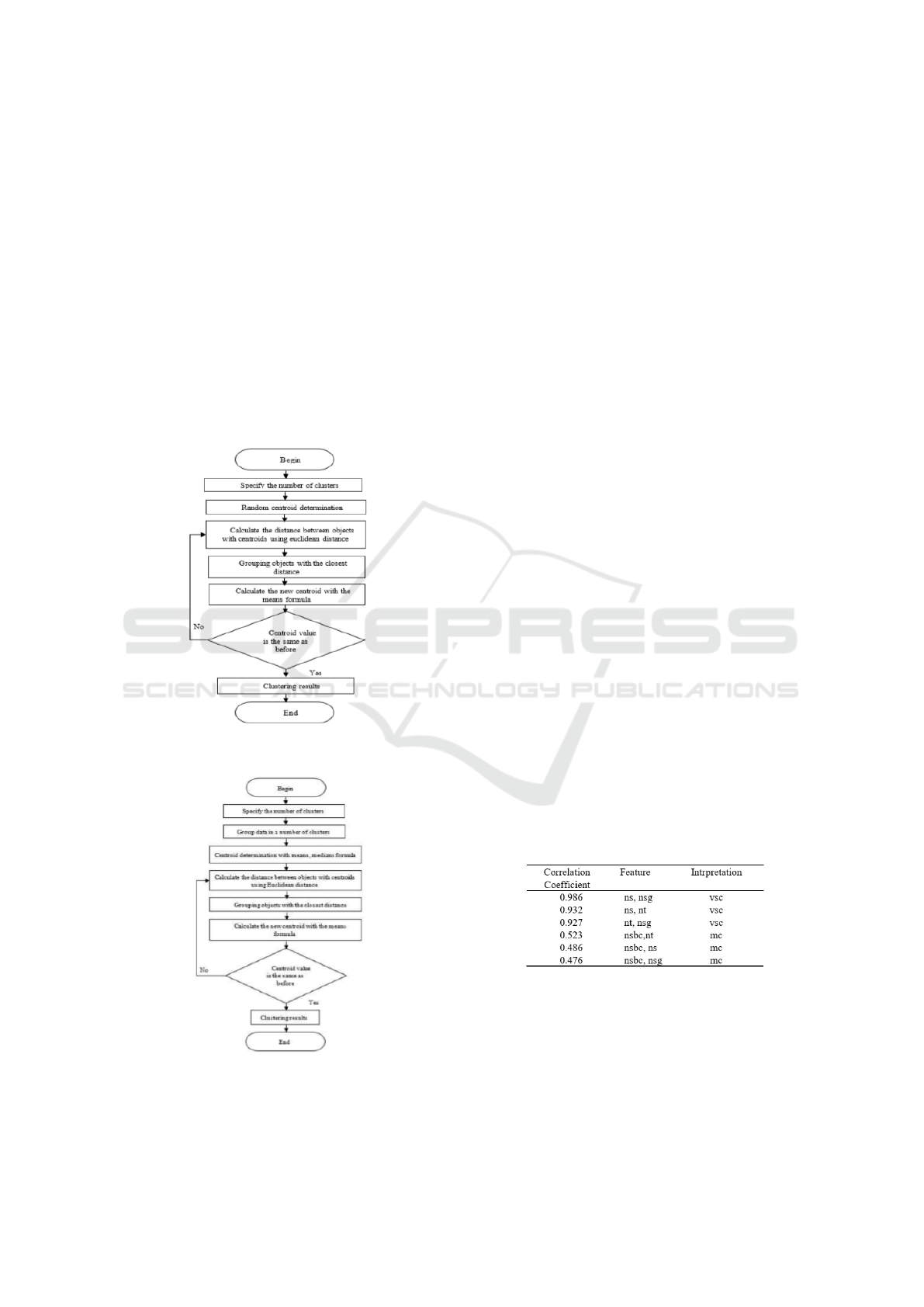
of the original K-Means algorithm are illustrated

in Figure 2and the proposed K-Means algorithm

by determining the initial centroid of the cluster

using the median formula and the mean formula

illustrated in Figure 3

Figure 2: Original K-Means algorithm

Figure 3: Proposed K-Means algorithm optimization

The sixth stage is Evaluation, evaluate the results

of the cluster using the Elbow method, this method

is a visual method to test the consistency of the best

number of clusters. The idea is to determine the num-

ber of clusters then add clusters, calculate the sum

squared error (SSE) per cluster until the maximum

number of clusters that have been determined, then

by comparing the difference SSE of each cluster, the

most extreme difference forming the angle of the el-

bow shows the best cluster number.(Bholowalia and

Kumar, 2014) (Madhulatha, 2012), here is the SSE

formula

SSE = Σ

i=1

x j∈C

||x

− µ

(8)

with xj is object in the cluster ci and centroid of the

cluster

The Elbow method algorithm in determining the

value of k in K-Means is as follows:

1. Initialization k = 1

2. Starting

3. Increment k value

4. Calculate SSE Y

5. Observe the value of SSE which drops dramati-

cally

6. The value of k at the SSE of a drastic decrease is

the optimal k value

7. End.

3 RESULTS AND DISCUSSION

In this study, the data preparation stage is performed

feature correlation analysis using Pearson Correlation

on data mining tools with the ﬁnal result using four

features with interpretation using the Pearson Corre-

lation coefﬁcient table (Schober et al., 2018), a com-

parison of correlations between features is presented

in Figure 4

Figure 4: Pearson Correlation Coefﬁcient result.

Base on Figure 4 it can be seen that features of the

number of students with the number of study groups,

the number of students to the number of teachers, the

number of teachers with the number of study groups

has a very strong correlation and the others has a mod-

erate correlation, then to eliminate the dominance of

attributes so the data is normalized using the min-max

K-Means Clustering Optimization using the Elbow Method and Early Centroid Determination Based-on Mean and Median

237

normalization method with the following results in

Figure 5

Figure 5: Sample of data normalization results.

Before the clustering process is carried out with

the K-Means algorithm the data is divided into a num-

ber of (k) clusters and the data is sorted from the

smallest to the largest value, this is done so that the

median and average group data can be calculated. The

results of the K-means clustering algorithm are very

dependent on the initial determination of the number

of clusters to be formed and the selection of the ini-

tial centroids on grouping objects in the cluster, re-

lated to these problems in this study conducted exper-

iments using the mean statistical formula, and the me-

dian formula to determine initial centroids compared

to random initial centroid determination to test the

effect of initial determination of centroids in the K-

Means algorithm on the number of iterations needed

to reach the data uniformity in the cluster formed. In

the KMeans algorithm, the initial determination of the

centroid is done by randomly selecting an object as-

suming each data object has a level of similarity to be

chosen as the initial centroid. In this research, the re-

sults of three clusters that represent the excess teach-

ing staff, the adequacy of the teaching staff and the

lack of teaching staff are needed then a random value

is used that refers to the initial, middle and end val-

ues to represent the distribution of existing data ob-

jects. The median formula is used in this experiment

as a representation of the mean value of the data in

the group assuming that the middle value is a coun-

terbalance to the minimum and maximum values that

exist in the data group, also conducted an experiment

with the average formula (mean) with the assumption

of representing all the values of objects in the group

because the mean formula divides all the values of

data objects in the group with the amount of data in

the group. The initial centroid value is taken from the

number of students as centroid 1, the number of teach-

ers as centroid 2, the number of subjects as centroid 3

and the number of study groups as centroid 4, here is

the centroid table of all clusters

space

Figure 6: Early centroid based-on median value.

Figure 7: Early centroid based-on median 2 value.

Figure 8: Early centroid based-on mean value.

Figure 9: Early centroid based-on minimum value.

Figure 10: Early centroid based-on maximum value.

Figure 11: Early centroid based-on random 1 value.

Figure 12: Early centroid based-on random 2 value.

Determination of the number of clusters that are

formed greatly affects the results of grouping data us-

ing K-Means clustering because this is the earliest

stage of this algorithm, if incorrectly determining the

number of clusters used will cause the number of iter-

ations needed to be more and allows there are empty

clusters that do not have members. In this study the

evaluation of determining the best number of clusters

to be used in clustering uses the Elbow method which

in principle observes the most drastic decrease in SSE

that forms the angle of the elbow, the evaluation re-

sults of determining the best cluster number in this

study are presented in Figure 13

CONRIST 2019 - International Conferences on Information System and Technology

238

space

Figure 13: Determination of the best cluster using the El-

bow method.

Graph in Figure 13 is arranged based on the sum-

mary results of the SSE total calculation experiment

from each number of clusters in the range of exper-

iments starting from 2 to 10 clusters which are pre-

sented in Table 11

Figure 14: Comparison table of the number of clusters with

SSE and the number of iterations needed.

Based on the Figure 13it can be observed that

the most drastic decrease in SSE refers to the num-

ber of clusters 3 with SSE difference at 2 data points

0.943396 then the SSE gradually decreases without a

drastic surge towards the lowest point forming an an-

gular angle between clusters 2, 3 and 5 so that from

observation in the graph forming a right angle, the

number of clusters 3 is the best number of clusters

to use. This is reinforced by the number of iterations

needed to achieve the convergence of cluster members

formed referring to the number of 3 clusters with 3 it-

erations needed or 25% less iteration than the number

of iterations needed if using another cluster.

Statistics on the results of the K-Means clustering

process with various experiments conducted are pre-

sented in the form of bar charts in Figure 15

Figure 15: Results of K-Means clustering with various cen-

troid value experiments.

Based on the Figure 15 The results of clustering

using the K-Means algorithm with initial determina-

tion of centroid values using various formulas can be

explained as follows, clustering KMeans using initial

centroid values based on the median formula (5) re-

quires 3 iterations with 6 members of cluster 1, 16

members of cluster 2 and 8 cluster members 3 while

the median-based centroid value based on formula (6)

requires the same iteration as the initial centroid based

on formula average (3) but has a difference in the

number of cluster members in clusters 2 and 3. The

cluster member results use a minimum based value

centroid is very much different in the number of clus-

ter members 2 and 3 compared to the results of the

cluster using other centroid values. Clustering uses

centroid values based on maximum values, random 1

value, random 2 value produces the same number of

members, namely 6 members in cluster 1, 14 mem-

bers in cluster 2, 10 members in cluster 3, but requires

a different number of iterations, centroid values based

on maximum values is the one that requires the most

iteration, as many as 6 iterations.

Based on the explanation of the experimental re-

sults that using the mean value requires a number of

iterations of 3 iterations or 22.58% lower than the av-

erage iteration using a random value that requires a

number of iterations of 4.75 iterations and the num-

ber of cluster members produced is more stable than

median and random values.

4 CONCLUSIONS

Based on the results of the clustering data experiment

using the K-Means algorithm with optimization of the

determination of the best number of clusters using

the Elbow method in terms of the iteration needed to

achieve the convergence of the members of the clus-

ter results 25% less than using the number of other

clusters and the determination of the initial centroid

using a mean formula is more consistent in producing

convergence of the number of members in the clus-

ter as well as the most efﬁcient number of iterations

with 22.58% less than the iteration needed if using a

random initial centroid determination.

K-Means Clustering Optimization using the Elbow Method and Early Centroid Determination Based-on Mean and Median

239

REFERENCES

Bholowalia, P. and Kumar, A. (2014). Ebk-means: A clus-

tering technique based on elbow method and k-means

in wsn. International Journal of Computer Applica-

tions, 105(9).

Draisma, J., Horobet¸, E., Ottaviani, G., Sturmfels, B., and

Thomas, R. R. (2016). The euclidean distance degree

of an algebraic variety. Foundations of computational

mathematics, 16(1):99–149.

Fabregas, A. C., Gerardo, B. D., and Tanguilig III, B. T.

(2017). Enhanced initial centroids for k-means algo-

rithm. International Journal of Information Technol-

ogy and Computer Science, 1:26–33.

Han, J., Pei, J., and Kamber, M. (2011). Data mining: con-

cepts and techniques. Elsevier.

Jain, S., Shukla, S., and Wadhvani, R. (2018). Dynamic

selection of normalization techniques using data com-

plexity measures. Expert Systems with Applications,

106:252–262.

Kodinariya, T. M. and Makwana, P. R. (2013). Review on

determining number of cluster in k-means clustering.

International Journal, 1(6):90–95.

Li, Y. and Wu, H. (2012). A clustering method based on

k-means algorithm. Physics Procedia, 25:1104–1109.

Liu, L., Peng, Z., Wu, H., Jiao, H., Yu, Y., and Zhao, J.

(2018). Fast identiﬁcation of urban sprawl based on

k-means clustering with population density and local

spatial entropy. Sustainability, 10(8):2683.

opez-Rubio, E., Palomo, E. J., and Ortega-Zamorano, F.

(2018). Unsupervised learning by cluster quality opti-

mization. Information Sciences, 436:31–55.

Madhulatha, T. S. (2012). An overview on clustering meth-

ods. arXiv preprint arXiv:1205.1117.

Sarkar, J. and Rashid, M. (2016). Visualizing mean, me-

dian, mean deviation, and standard deviation of a set

of numbers. The American Statistician, 70(3):304–

312.

Schober, P., Boer, C., and Schwarte, L. A. (2018). Corre-

lation coefﬁcients: appropriate use and interpretation.

Anesthesia & Analgesia, 126(5):1763–1768.

Shakeel, P. M., Baskar, S., Dhulipala, V. S., and Jaber,

M. M. (2018). Cloud based framework for diagnosis

of diabetes mellitus using k-means clustering. Health

information science and systems, 6(1):16.

Simovici, D. A. and Djeraba, C. (2014). Clustering. In

Mathematical Tools for Data Mining, pages 767–817.

Springer.

Szelkagowska-Rudzka, K. (2018). Human resources man-

agement in higher education institutions in poland.

Management, 22(1):208–225.

Tzortzis, G. and Likas, A. (2014). The minmax k-

means clustering algorithm. Pattern Recognition,

47(7):2505–2516.

Wilks, D. S. (2011). Cluster analysis.

CONRIST 2019 - International Conferences on Information System and Technology

240