Urban Traffic Jam Time Prediction Mode

Zhixu Gao

1, a, *

, Guyue Tian

2, b

, Fengsi Yu

2, c

School of physics and electronic information, Yunnan Normal University, Yunnan 650500, China

College of Science, Chongqing University of Technology, Chongqing, 401320, China

Keywords: Survival analysis model; Traffic congestion; Predictive model.

Abstract: Urban transportation is the core of urban social activities and economic activities. However, due to the

increase of population and motor vehicles, traffic congestion is caused by many factors. This paper established

a traffic congestion duration model based on survival analysis. The purpose is to use the model to obtain the

relationship between congestion index and congestion time, and improve the accuracy of prediction. Using

the nonparametric method to calculate, after defining the Shanghai Expressway survival function and risk

function, combined with the compiled data, calculate whether it is the impact of the working day on traffic

congestion, and the difference between the early, middle and late peaks for traffic congestion. The result can

be obtained: Traffic congestion on workdays is higher than on weekends, and traffic congestion is longer than

weekends.

1 INTRODUCTION

With the development of technology, people's

transportation is more convenient and intelligent.

Existing navigation software typically acquires real-

time GPS data through a taxi or vehicle in which the

software is installed to determine current road

conditions. Many navigation softwares have

introduced smart travel features to help people plan

the best route for travel and predict travel time. The

predictive congestion principle of navigation is to use

the speed prediction algorithm to calculate the vehicle

speed, and to update the timing according to the

driving information of the car, and then re-calibrate

and calculate. (Zhu Fuling, 2006)

However, with the increasing number of cars,

traffic congestion in cities is becoming more and

more serious, and traffic jams in urban traffic often

occur. (You Zhaoquan, 2018) Therefore, it is

practical to improve the prediction accuracy of

navigation through mathematical methods. It can

provide a guiding plan for the development of traffic

congestion control and guidance strategies. (Xiong

Li, Lu Yue, Yang Shufen, 2017)

2 DATA COLLECTION

We consult the relevant literature to collect the GPS

information of 10,000 taxies in Shanghai city on April

20,2017 (Shanghai Traffic Travel Network, 2019).

Since the data is too large, we sort out some of the

data in the table below. Please check the detailed data

in supporting documentation in appendix. The

following gives data analysis for taxies in Shanghai.

As can be seen from the table 1, the data we collected

included the latitude and longitude and instantaneous

travel speed of each tax

3 MODEL BASED ON SURVIVAL

ANALYSIS OF TRAFFIC

CONGESTION DURATION

Survival analysis is a statistical method that analyzes

and infers the survival time of living things, people,

and other things like survival rules based on

experimental or survey data. It is also called risk rate

model or continuous model. The survival analysis

methods mainly include three methods: parametric

method, semiparametric method and nonparametric

method. When the distribution type is unknown, the

nonparametric method has higher computational

efficiency.

Gao, Z., Tian, G. and Yu, F.

Urban Trafﬁc Jam Time Prediction Mode.

DOI: 10.5220/0010019600380041

In Proceedings of the International Symposium on Frontiers of Intelligent Transport System (FITS 2020), pages 38-41

ISBN: 978-989-758-465-7

3.1 Establishment of Model

3.1.1 Traffic Congestion Probability

Distribution

According to the probability statistics, the probability

distribution of the capital vehicle is represented by a

distribution function, and the function is as follows.

    

Ft PT t f xdx





lim

dF t P t t t

dt t









，

Where



represents distribution function,

represents probability,

Indicates the duration of

traffic congestion,



Indicates the probability

density of the moment.

3.1.2 Calculation of Congestion Duration

Survival Function

The congestion duration survival function is

expressed as a survival rate, which indicates the

probability that the congestion duration is greater

than, and its expression is as follows. When the

survival probability is low, the survival curve is steep.

When the survival probability is high, the survival

curve is flat.

     

tPTt fxdx Ft



 



3.1.3 Traffic Congestion Risk Function

The risk function refers to the probability that traffic

congestion does not disappear after the moment

occurs, but disappears in a very small time period



, also called the conditional survival probability. The

risk function can also be expressed by the distribution

function



and the probability density function



. The formula is as follows:









lim

Pt T t tT t

tft

ht st

tstdF



 





The cumulative risk function curve is obtained by

integrating the risk function. The higher the position,

the higher the probability of ending the traffic

congestion event in Δt.

3.1.4 Nonparametric Kaplan



Meier

Method

Suppose there are n traffic congestion duration

samples, the duration period has k different values,

and they are directly arranged from small to large

12 k

tt t





. The survival function of the traffic

congestion duration is the estimation function of





as shown in equation:











Where

is the number of samples that existed

before the moment

, that is, the sample size that

traffic congestion continues to be;

is the number of

samples for which congestion has ended during this

unit time period

;



is the probability of

survival for the moment

In this practice, the survival function has a simple

estimation method because there is no censored data.

Since the congestion duration in this paper is a

complete sample, that is, the exact congestion

duration is known during the observation time, there

is no censored data. Therefore, the survival function

can be estimated by the proportion of the number of

samples whose congestion duration is longer than





Here





is an estimate of





, indicating the

probability that the congestion duration is longer than

if a congestion event has occurred. The risk

probability formula is expressed as follows:



Bt B





Then get the average risk rate: the number of

samples ending in the unit time interval of a unit

divided by the number of samples in the interval

Urban Trafﬁc Jam Time Prediction Mode

where the conceptual congestion does not end, the

formula is as follows:





Where A is Number of samples ending in

congestion at the beginning of time T; B is Number

of samples with no congestion after time T; C is

Number of samples congested per unit time after time

T; D is Number of samples ending in the interval.

t

is Interval width.

3.2 Result of the Model

Calculate the survival function of Shanghai working

days and weekends based on the existing data as

shown in Fig1. (Si Sukui, 2011)

Fig 1: Traffic congestion index.

By calculating the survival function of weekdays

and weekends

=0.0039p

, it is shown that both are

significant. Known from Fig 1. The working day

survival function is above the weekend survival

function, indicating that the traffic congestion

frequency on the working day is higher than the

weekend, and the traffic congestion duration is longer

than the weekend. On weekends, the traffic

congestion duration is 85.4% within 250min. The

traffic congestion is likely to end at the end of the

traffic congestion period. The traffic congestion is

less likely to be exceeded. The working day traffic

congestion duration is less than 300min. %, the traffic

congestion is more likely to end the congestion

period, and the possibility of traffic congestion is less

than the duration. To further compare the difference

in traffic congestion duration between weekends and

weekdays, we compare the risk function based on the

traffic congestion duration model of survival analysis,

as shown in Fig 2.

Fig 2: Survival coefficient.

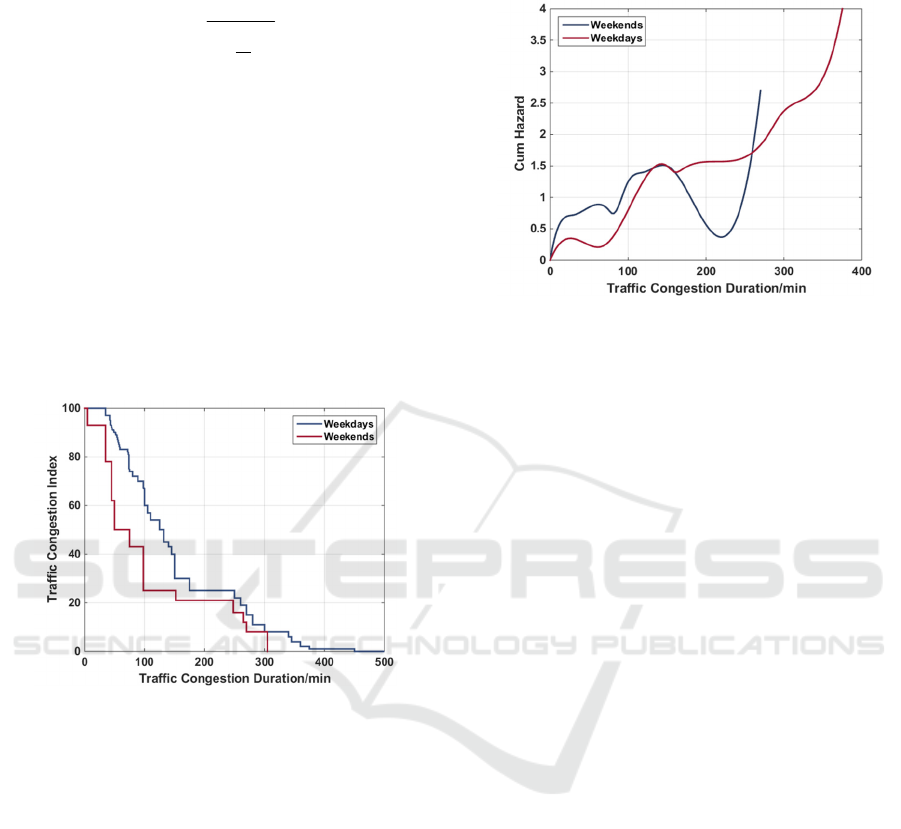
It can be seen from the Fig 2 that when the traffic

congestion duration is between 0 and 165 min or

greater than 275 min, the risk function of the working

day is less than the weekend risk function, indicating

that when the traffic congestion duration is within the

interval, the same congestion duration, It is easier to

end the congestion on weekends. When the

congestion duration is less than 165min or greater

than 275min, the risk function of the weekend is less

than the working day. Under this condition, the

working day is more likely to end the congestion

under the same traffic congestion duration. This is

consistent with the working day due to commuting

travel demand.

4 CONCLUSION

A traffic congestion duration model based on survival

analysis is established. The purpose is to use the

model to obtain the relationship between congestion

index and congestion time, and improve the accuracy

of prediction. Using the nonparametric method to

calculate, after defining the Shanghai Expressway

survival function and risk function, combined with

the compiled data, calculate whether it is the impact

of the working day on traffic congestion, and the

difference between the early, middle and late peaks

for traffic congestion. Get: Traffic congestion on

workdays is higher than on weekends, and traffic

congestion is longer than weekends. The traffic

congestion in the afternoon peak and the evening

peak is longer than the early peak. The traffic

congestion in the afternoon peak actually lasts until

the evening peak.

FITS 2020 - International Symposium on Frontiers of Intelligent Transport System

REFERENCES

Shanghai Traffic Travel Network. Interpretation of Traffic

Index [EB/OL].htt p://www. j tcx.sh.cn/zhishu/ j

iedu.html,2019-11-22

Si Sukui. Mathematical Modeling Algorithm and

Application [M]. National Defense Industry Press,

2011.

Xiong Li, Lu Yue, Yang Shufen. Study on Urban Road

Traffic Congestion Prediction and Duration[J].

Highway,2017,62(11):125-134.

You Zhaoquan. Research on Traffic Congestion Prediction

Based on Hadoop Big Data Platform [D]. Chinese

People's Public Security University, 2018.

Zhu Fuling. Research on Urban Road Traffic Congestion

Evaluation Index System [D]. Southeast University,

2006.

Urban Trafﬁc Jam Time Prediction Mode