
Detection of Ball Spin Direction using Hitting Sound in Tennis
Naoki Yamamoto
1 a
, Kenji Nishida
1 b
, Katsutoshi Itoyama
1 c
and Kazuhiro Nakadai
1,2 d
1
School of Engineering, Tokyo Institute of Technology, Tokyo, Japan
2
Honda Research Institute Japan Co., Ltd., Saitama, Japan
Keywords:
Sports Science, Tennis, Acoustic Analysis of Impact, Ball Spin Detection.
Abstract:
This paper describes the detection of rotation direction using the hitting sound of tennis balls. Since each
ball rotation direction has a slightly different rotation direction and trajectory, there should be a difference
in the hitting sound. To distinguish the characteristics of ball rotation direction, a database was constructed
that combines the hitting sound recorded experimentally with ball rotation direction. Since it is difficult
to distinguish audible differences in hitting sounds by ear, it is necessary to identify them using measuring
instruments. For this purpose, after extracting the amplitude spectrum by fast Fourier transform of the shot
sound, the entire data was normalized and classified by a support vector machine. As a result of evaluating this
method, a high accuracy was obtained in identifying the sound associated with slice among other hit sounds.
The proposed method also evaluated the ball hit sound from a YouTube video in an unknown environment and
achieved a perfectly correct identification of spin and slice.
1 INTRODUCTION
In recent years, there has been a growing movement
worldwide to introduce science and technology
into sports. Smart courts (SecondSpetrum, 2020;
Playsight, 2020), which have multiple cameras that
can track the movement of players and balls using
Figure 1: Smartsensor can be attached to the grip end of
the racket and can measure the rotation direction, speed,
rotational speed, etc. of the stroke.
a
https://orcid.org/0000-0001-7367-4725
b
https://orcid.org/0000-0003-4214-4005
c
https://orcid.org/0000-0002-7098-3896
d
https://orcid.org/0000-0002-6134-4558
computer vision technology, are utilized in various
sports such as football, basketball, and so on (Seo
et al., 2018). The smart court system developed to
improve the accuracy of umpire decisions in tennis in-
troduced “Hawkeye” which includes eight super high-
speed cameras to specify the trajectory and landing
point of the ball (Baodon, 2014) to inform umpires in
professional matches and to smoothly advance games.
However, smart courts require large systems to be
installed and their cost prohibit personal use. Form
(pose) analysis is an important issue in computer vi-
sion for sports in which many studies have been re-
ported (Cust et al., 2019; Appelbaum and Erickson,
2018; Okamoto et al., 2015; Cao et al., 2019). Such
studies have achieved significant progress in many
sports, but one important issue has not been studied
well in ball games – the detection of the spin (or rota-
tion) direction of balls.
The trajectory of a ball is greatly affected by its
rotation, so players need to be able to detect the rota-
tion direction to predict the ball trajectory. In tennis
especially, players need to be able to perform balls
with various rotation and also identify the rotation di-
rection of the opponents’ balls. A smart tennis sen-
sor (Zepp, 2020) has been developed to measure ball
speed, rotation direction and revolution using an ac-
celerometer and three-axis gyro-sensor, which is usu-
ally attached to the grip-end of the racket (Figure 1).
30
Yamamoto, N., Nishida, K., Itoyama, K. and Nakadai, K.
Detection of Ball Spin Direction using Hitting Sound in Tennis.
DOI: 10.5220/0010107600300037
In Proceedings of the 8th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2020), pages 30-37
ISBN: 978-989-758-481-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Players can learn to hit various rotation directions by
using smart tennis sensors, but they do not provide in-
formation about the opponent’s treatment of the ball.
Ball rotation can be detected using a high-speed and
high-resolution camera, but since tennis is a sport in
which the balls travel fast in a short period of time,
and are hit at various places in the court, a precise
tracking system is required in addition.
Since tennis players are known to make decisions
based on the hitting sound of the opponent, in this
study, we focused on the hitting sound. Although
some previous studies focused on the hitting sound
of tennis balls during play, they paid attention only to
ball speed (Zhang et al., 2017). In depth research on
hitting sound and ball rotation direction has not been
previously conducted. However, Canal-Bruland et al
asked subjects to watch a professional tennis match
on video and predict the trajectory of the ball at that
time (Canal-Bruland, 2018). As a result, it was shown
that the hitting sound could be an important factor in
predicting the ball trajectory. In predicting the tra-
jectory of a ball, three types of the rotation direc-
tion, namely spin, flat, and slice form the basis of ball
movement pattern. By recognizing rotation direction,
a rough trajectory of the ball can be predicted, and
player performance can improve as prediction accu-
racy improves.
A spin hit happens when the head of the racket is
rotated over the top of the ball during a hit causing a
tangential velocity of the top of the ball in the same di-
rection as the ball’s trajectory resulting in lower drag
force at the bottom of the ball so it falls downwards
(Figure 2a). A flat hit ball does not spin to any sig-
nificant degree so does not veer from the direction in
which it is hit (Figure 2b). A slice hit, contrary to
spin, happens when a player angles the racket back
and slides it underneath the ball when hitting which
makes it veer upwards. The tangential velocity of the
top of the ball is in the opposite direction of the tra-
jectory of the ball, so the force of this hit tends to
be weaker than spin or flat. Players may also make
the ball deflect left or right by corresponding rota-
tions (Figure 2c). To validate the proposed method,
a set of tests was, performed to obtain necessary ball
hitting sound data. Then, a identifiable data set was
constructed using a developed identifier. Thereafter,
accuracy of the identifier was evaluated. Finally, we
sampled ball hitting sounds from YouTube and ap-
plied the identifier to observe the percentage of cor-
rect answers.
Following, Section 2 describes related research,
Section 3 describes the database constructed, Section
4 proposes a method for processing the data, and Sec-
tion 5 describes the results and considerations of eval-
uation experiments using the proposed method.
2 RELATED RESEARCH
To improve player performance in tennis, Asano et al.
attached markers to a ball and used high-speed cam-
eras to determine the rotation angle and number of ro-
tations for each of three axes. Three-dimensional lo-
cation of the ball center was obtained from the camera
parameters with two cameras, and the ball trajectory
was estimated.
Elsewhere, research has focused on the sound of
hitting balls in sound table tennis. A game was de-
signed for blind people with a rule that if no returned
ball hitting sound was heard, it was a foul. Because
the judge only relied on hearing, application of the
rule was ambiguous. Kogusuri et al. aimed to clarify
this rule (Kogusuri et al., 2008). In that research, they
propose a technique to determine a hit by focusing on
frequency domain components by recording the hit
sound with a digital audio tape recorder via a noise
meter, applying wavelet transform analysis, and us-
ing the hit sound. Similar concept was used aimed at
improving the player performance in other ball sports
studies focusing on the hitting sound. Although the
effect of ball hitting sound on performance has been
studied, waveform characteristics of the hitting sound
have not been clarified.
Therefore, Zhang et al. are conducting research of
the latent characteristics of the hitting sounds of op-
ponent players (Zhang et al., 2017). In their study,
the sound of hitting a service ball was extracted from
the deuce side and the advantage side in 15 examples
each, and the characteristics were compared by over-
lapping the time domain waveforms. Specifically, a
television image was recorded and its sound was ex-
tracted, the first peak of each sound waveform was
overlapped and compared for each player, and the
sound characteristics of each player were detected
from the average amplitude of the first peak and the
arrival time between the first peak and the last peak.
It is defined that a sample point has a peak when it
has a greater value than two adjacent sample points
and a certain threshold. It is how to find peaks. They
reported a correlation between ball speed and hitting
sound magnitude, but rotation direction was not men-
tioned.
Hitting sound has been studied in other sports.
However, in tennis, although some studies aimed at
improving performance focused on the sound of hit-
ting balls, no study has been conducted to determine
ball rotation from the sound of hitting balls as far as
we know. In this study, we focused on ball hitting
Detection of Ball Spin Direction using Hitting Sound in Tennis
31

Direction of Travel
Direction of Racket Swing
Direction of Rotation
(a) Spin rotation direction.
Direction of Travel
Direction of Racket Swing
(b) Flat rotation direction.
Direction of Travel
Direction of Racket Swing
Direction of Rotation
(c) Slice rotation direction.
Figure 2: Three types of rotational directions.
sound to describe and identify rotation direction.
3 METHODS AND
CONSTRUCTION OF BALL
HITTING SOUND DATABASE
This section describes experiments to construct a hit-
ting sound database, and processing algorithm to con-
struct a hitting sound pattern database from collected
sound data.
3.1 Recording Exercise
The purpose of this exercise was to record spin, flat,
and slice shot sounds and create a basic pattern data
set to identify rotation directions. The recording was
performed under the following conditions.
• Date & Time: 2019/12/10 11:00-13:00
• Place: Ninomiya Park Tennis Court (hard court,
outdoor), Tsukuba City, Japan
• Weather: Sunny & almost no wind
• Hitter: A male, 15 years of tennis experience
Figure 3 illustrates the experimental setting, and
Table 1 shows specifications of the equipment used in
the recording. The hitting procedure is controlled to
maintain the quality of recorded sounds as follows:
1. A ball person throws a ball for a hitter.
2. The hitter hits the ball with a certain direction and
force which is decided by the hitter.
3. The hitter tells a recorder the rotation direction
(and force) that the hitter decided.
In total, 92 trials were performed.
3.2 Ball Hitting Sound Database
Construction
For each recorded sound, a 50 ms clip was extracted
so that each clip can include the moment of impact.
This was manually done for all 92 recorded sound
Table 1: Equipment used in the recording.
Equipment Description
Microphone type TAMAGO-03
Microphone position 2 near the pillars con-
nected straight to PC
Tennis ball 20 new balls
Racket SRIXON REVO CV3.0
(SR21802)
PC 16 kHz and 16-bit record-
ing
data using Audacity. We, thus, collected a ball hit-
ting pattern dataset consisting of 92 sound clips and
the corresponding rotation direction.
Ball trajectory
USB cable
Microphone
Ball person
Hitter
PC
Figure 3: Experimental setup. A ball person throws a ball,
and a hitter hits the ball. Arrows show a typical trajectory
of the ball for a single trial.
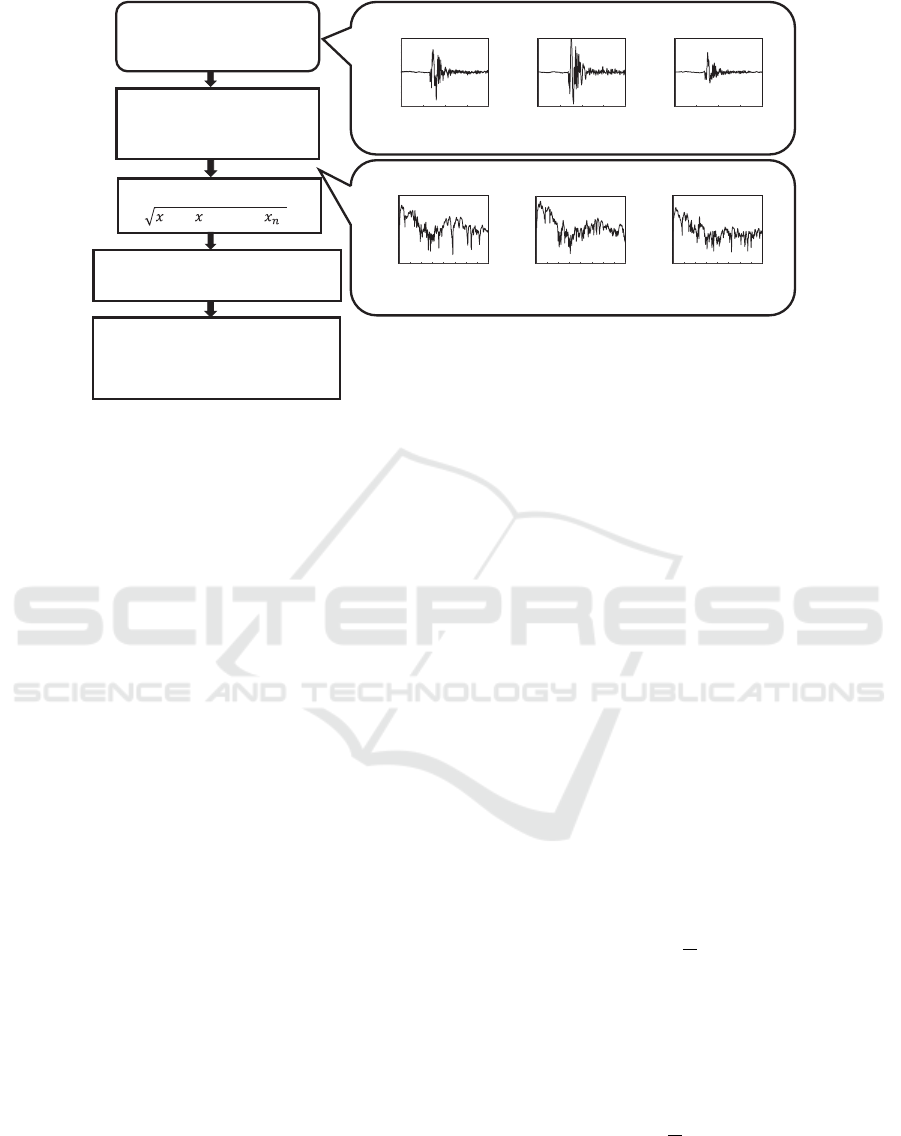
4 PROPOSED METHOD
This section explains the proposed method to identify
rotation direction from hitting sound. The proposed
method uses frequency analysis, data normalization,
dimensionality reduction, and 2-class SVM to clas-
sify the ball rotation (Figure 4).
icSPORTS 2020 - 8th International Conference on Sport Sciences Research and Technology Support
32
slice
Input: Amplitude spectrum (91dim)
Output: Ball rotation (spin, flat, slice)
Normalization
1
2
+
2
2
+ ⋯ +
2
Constructed dataset
spin
amplitude spectrum
spin
flat
slice
Frequency analysis
Window length: 800
FFTsample point: 1024
flat
Recorded hitting sound
Sampling frequency: 16kHz
Length of sound: 50ms
Support vector machine
Principal component analysis
0 200 400 600 800
Time (sample)
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Amplitude
0 200 400 600 800
Time (sample)
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Amplitude
0 200 400 600 800
Time (sample)
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Amplitude
0 1 2 3 4 5 6 7 8
Frequency (kHz)
-50
-40
-30
-20
-10
0
10
20
30
Amplitude (dB)
0 1 2 3 4 5 6 7 8
Frequency (kHz)
-50
-40
-30
-20
-10
0
10
20
30
Amplitude (dB)
0 1 2 3 4 5 6 7 8
Frequency (kHz)
-50
-40
-30
-20
-10
0
10
20
30
Amplitude (dB)
513dimЍ 91dim
Figure 4: Flowchart of the proposed method.
4.1 Frequency Analysis
The input sound pattern is assumed to have 50 ms du-
ration including the impact of hitting as described in
Section 3. Fourier transform is performed for the in-
put signal. Fourier transform is a frequency analysis
method used to decompose a complex sound into its
constituent parts, and there is an algorithm to greatly
increase the speed of the discrete Fourier transform,
which is called fast Fourier transform (FFT). FFT is
beneficial when dealing with a large amount of data,
and thus we decided to use FFT with a rectangular
window for frequency analysis. In the present case,
the number of data sets to be processed was 92. Since
the sampling frequency was set at 16 kHz and the time
component of clipped signals was 50 ms, the length
of the signal was 800 samples. For FFT, the win-
dow length of 1024 samples with zero padding was
adopted. When FFT is applied, the real part of the
frequency-amplitude diagram is line-symmetric, the
imaginary part is point-symmetric, that is, it is con-
jugate, and the amplitude spectrum is line-symmetric.
Therefore, the frequency component of interest at this
time was 0–8 kHz (Nyquist frequency). Thus, the
number of dimensions of the data to be treated this
time was 513 dimensions. The analysis was per-
formed using MATLAB.
4.2 Data Normalization
Normalization was performed to prevent variation due
to the difference of the impacted position for each
data.
4.3 Dimensionality Reduction with
Principal Component Analysis
Since only 92 samples with a 513 dimensional fea-
ture representation for each impact sound were ob-
tained, the training samples should be mapped to the
lower dimensional feature space to ensure good gen-
eralization performance. Principal component anal-
ysis (PCA) (Diamantaras and Kung, 1998) estimates
principal components of a dataset, where a principal
component with a larger score gives better representa-
tion of the dataset. By selecting principal components
with larger scores, the dataset is well represented with
a lower dimensional feature space. Therefore, we
applied the Principal Component Analysis (PCA) to
our impact sound data. The procedure of PCA is de-
scribed as follows. Let x
i
(i = 1,..., N) represent the
i-th D-dimensional data. The DC offset is first re-
moved by,
˜
x
i
= x
i
−
1
N
N
∑
j=1
(x
j
). (1)
DC offset is the addition of a Direct Current compo-
nent to a device’s performance and the effect of sur-
rounding electrical influences that causes it to deviate
from 0V.
The covariance matrix of X is, then, calculated as,
Σ
X
=
1
N
N
∑
i=1
˜
x
i
˜
x
T
i
. (2)
Eigenvalue decomposition is performed for the ob-
tained covariance matrix X by,
Σ
X
U = UΛ, (U
T
U = I), (3)
Detection of Ball Spin Direction using Hitting Sound in Tennis
33

0 100 200 300 400 500
Feature dimention
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Contribution rate
Figure 5: Cumulative contribution rates of PCA for the con-
structed database. The horizontal axis is the dimension of
rotation direction and the vertical axis is the cumulative con-
tribution rate at the selected feature dimension.
where U is the square D×D matrix whose i-th column
is the eigenvector, and Λ is the diagonal matrix whose
diagonal elements are the corresponding eigenvalues.
Figure 5 shows a cumulative contribution rate for
first 91 principal components in the descending order.
Since the cumulative contribution rate reached 1 with
the 91 principal components, the number of dimen-
sions was set to 91 in the feature vector for identifica-
tion. Note that due to rank deficient, the rate reached
1 with 91 principal components for 92 samples. In
Figure 5, the rate also reached 0.7 with 20 principal
components, and we will also verify a lower feature
such as a 20-dimensional feature in the evaluation.
4.4 SVM
The proposed method performs two-class classifica-
tion. For example, when a target is spin, the iden-
tification is to discriminate whether the sound is for
spin or not. This means that three types of two-class
identification, that is, for spin, flat, and slice were per-
formed.
For the low dimensional input vector, s, obtained
by PCA, we first introduce a general classification
function, y, defined as,
y = sign
(
w
T
s − h
)
, (4)
where w indicates a weight vector for the input and
h is a threshold. Function sign(u) is a sign func-
tion, which outputs 1 when u > 0 and outputs -1 when
u ≤ 0. In other words, Eq. (4) separates a space rep-
resented by s into two sub-spaces using a separating
hyperplane defined by w. An SVM (Scholkopf et al.,
1999; Vapnik, 1998) is a method to determine the sep-
arating hyperplane that maximizes the distance (mar-
gin) between the separating hyperplane and the near-
est sample. However, in a conventional SVM, all in-
put samples should be linear separable, which is de-
Table 2: The number of data and class weight.
Identifier spin flat slice
positive sample 46 16 30
negative sample 46 76 62
q
i
1 5 2
fined by,
(w
T
s
i
− h) ·t
i
≥ 1, i = 1,...,N, (5)
where t
i
shows the correct class label (1 or −1) for s
i
.
s
i
stands for the i-th input vector.
This means that the samples are separated by two
hyperplanes such as
H1 : w
T
s
i
− h = 1, (6)
H2 : w
T
s
i
− h = −1, (7)
and there are no samples between these two hyper-
planes. The distance between the separating hyper-
plane and each of these hyperplanes is defined as
1/∥w∥.
To relax a linear separable constraint, a soft-
margin is introduced to SVM, which allows training
samples between H1 and H2. For this, a distance pa-
rameter ξ
i
for s
i
is introduced. It is defined for the i-th
sample with t
i
= 1 as,
ξ
i
=
{
−w
T
s
i
+ h + 1 (w
T
s
i
− h < 1)
0 (otherwise)
(8)
It is also defined for the i-th sample with t
i
= −1 as,
ξ
i
=
{
w
T
s
i
− h + 1 (w
T
s
i
− h > −1)
0 (otherwise)
(9)
The soft-margin SVM is, then, defined as an opti-
mization problem to minimize a cost function defined
by,
L(w,ξ) =
1
2
∥w∥
2
+C
N
∑
i=1
q
i
ξ
i
(10)
subject to
ξ
i
≥ 0, t
i
· (w
T
s
i
− h) ≥ 1 − ξ
i
, (i = 1, . . .,N), (11)
where ξ = {ξ
i
|i = 1,··· ,N}. C stands for a cost pa-
rameter for ξ. q
i
is a weight for the i-th sample defined
by,
q
i
=
{
1 s
i
∈ C
l
|x ∈ C
l
|/|x ∈ C
s
| s
i
∈ C
s
(12)
where C
s
and C
l
indicate the smaller and the larger
class, respectively.
Mentioned above, there are three types of identi-
fiers such like Table 2.
icSPORTS 2020 - 8th International Conference on Sport Sciences Research and Technology Support
34

Solving this problem with an optimal solution α,
the classification function can be redefined as
y = sign (w
T
s − h)
= sign (
∑
i∈S
α
i
t
i
s
T
i
s − h). (13)
where S stands for the indices of the support vectors.
The samples are grouped with α
i
; a sample s
i
is classi-
fied correctly when α
i
= 0, when 0 < α
i
< C the sam-
ple s
i
is also classified correctly and it locates on the
hyperplane H1 (or H2) as a support-vector, if α
i
= C
the sample s
i
becomes a support-vector but it locates
between H1 and H2 with ξ ̸= 0.
The recorded signal data was fed into the support
vector machine (SVM). The number of data examples
was 92. Therefore, a method called the Leave One
Out Cross-Validation (LOOCV), which splits up the
sample into two categories: validation data, made up
of one data from the sample, and training data, made
up of the rest of the data in the sample, was used to ex-
amine the data. The sample was given a class weight,
and the classification was carried out accordingly. Us-
ing LOOCV is advantageous as it prevents overfitting
for few data, as observations are made on N-1 sam-
ples.
The present method identifies one rotation direc-
tion and others, such like spin and not spin (flat and
slice). Then, using the hyperparameter optimization
function in MATLAB, the parameter of the soft mar-
gin in which the accuracy was at maximum, was set.
5 EVALUATION
The proposed method is validated with the con-
structed ball hitting sound database and sound clips
selected from YouTube videos.
5.1 Identification with Recorded Ball
Hitting Sound Database
Each recorded sound clip was fed into the support
vector machine (SVM) as an input. The data set was
as small as 92, and the evaluation was performed by
LOOCV explained in the previous section in order to
prevent over-fitting and to maintain open test.
For each rotation, the hyper parameters such as a
soft margin were optimized using MATLAB to maxi-
mize the accuracy.
Figures 6a-6c illustrate the answer rates for identi-
fication of spin, flat, and slice from the sound clip us-
ing the constructed ball hitting sound database. The
horizontal axis of each figure shows the number of
feature dimensions up to 91 in the descending order
Table 3: Confusion matrix for identification of each ball
rotation direction. All 92 samples were identified with 91
dimensional features.
(a) Confusion matrix for identification of spin and oth-
ers.
spin (correct) others (correct)
spin
(prediction)
35 10
others
(prediction)
11 36
(b) Confusion matrix for identification of flat and oth-
ers.
flat (correct) others (correct)
flat
(prediction)
11 14
others
(prediction)
5 62
(c) Confusion matrix for identification of slice and
others.
slice (correct) others (correct)
slice
(prediction)
27 11
others
(prediction)
3 51
of eigenvalues. It is clear that, the accuracy is over
70% for all rotation directions. It is remarkable that
the accuracy with 91 dimensions is almost identical to
that with 20 dimensions. In other words, the analysis
can be effectively and accurately performed with 20
dimensions.
Tables 3 show confusion matrices of 2-class iden-
tification tasks with 91 feature dimensions. Each table
illustrates true-positive, true-negative, false-positive,
and false-negative scores of the identification task. As
mentioned above, accuracy of more than 70% was ob-
tained for all three rotations , but the precision has
different characteristics. The precision of identifying
flat is remarkably low like 44%, while the precision of
identifying spin and slice exceeds 70%. This is also
linked to the low F value for flat.
5.2 Analysis of YouTube Clips
To apply the proposed method to YouTube clips, a
video including ball hitting sounds by a professional
tennis player were selected. The selected video is of
the world’s fourth-ranked Roger Federer practicing at
the Australian Open (hard court) in January 2020
1
.
From the video, 5 spin samples and 5 slice samples
were picked up. After that, 50 ms ball hitting sound
clips were extracted from each video in the same man-
1
https://youtu.be/hTn42aJIhk8
Detection of Ball Spin Direction using Hitting Sound in Tennis
35

0 10 20 30 40 50 60 70 80 90
Feature dimension
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Accuracy
(a) Accuracy for spin.
0
10
20
30
40
50
60
70
80
90
Feature dimension
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Accuracy
(b) Accuracy for flat.
0 10 20 30 40 50 60 70 80 90
Feature dimension
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Accuracy
(c) Accuracy for slice.
Figure 6: Accuracy for each spin direcsion. The horizontal and vertical axes indicate the feature dimension and the accuracy
of two class identification between one rotation direction and others, respectively. The accuracy is defined as the number of
correctly identified sounds divided by the total number of sounds.
Table 4: Confusion matrix for hitting sound identification.
It uses 91 feature dimensions.
(a) Identification result of spin and others from
YouTube clips.
spin (correct) others (correct)
spin
(prediction)
5 0
others
(prediction)
0 5
(b) Identification result of slice and others from
YouTube clips.
slice (correct) others (correct)
slice
(prediction)
5 0
others
(prediction)
0 5
ner as it was done when constructing the database.
Since the sampling rate of YouTube video sound is
44100 Hz, it was resampled at 16 kHz using the Au-
dacity. Since overtaking from experiment result, the
number of feature dimensions was set to 91.
Tables 4a and 4b show the results of identifica-
tion for spin and slice, respectively. All 10 clips from
YouTube were 100% identified.
5.3 Discussion
This section discusses the results obtained from
the experiments using our own recorded sound and
YouTube clips. Not only our own recorded data but
YouTube data were successfully identified with high
accuracy. One problem is that identification perfor-
mance for flat shots was poor. This problem is con-
sidered to be caused by a small number of flat data.
The training data set consists of 46 spin, 16 flat and
30 slice shots. The lack of flat data and data unbal-
ancing between three kinds of shots resulted in poor
precision for flat data identification. Generally speak-
ing, when focusing on an individual tennis player, it is
natural that spin and slice are easy to be distinguished
from each other, but flat is difficult to be detected.
This will be supported by the fact that spin and slice
are in the opposite direction of rotation, and flat has
less rotation, that is, between spin and slice.
When the first principal component is analyzed,
we found that many of determining features are re-
lated to a frequency range 250-1100 Hz. This shows
that relatively a low frequency range is needed for
good identification although a hitting sound is impul-
sive with wide spectrum.
6 CONCLUSION
This paper describes identification of the rotation di-
rection of tennis ball from hitting sound. We consid-
ered three class identification, that is, spin, flat, and
slice, and proposed a rotation direction identification
method based on support vector machine and princi-
pal component analysis. We also constructed a hitting
sound database consisting of 92 hitting sounds with
labels. Using the constructed database, the accuracy
of spin identification was over 70% for each of three
classes, although the precision of flat was only about
44% due to unbalanced data and the small number of
flat data. The proposed method was also applied to
10 clips selected from YouTube, and in all cases the
shots were successfully identified. Our detail analy-
sis showed that the first principal component depends
heavily on 250-1100 Hz features, which is interesting
because hitting sound is impulsive with a lot of high
frequencies in the spectrum.
icSPORTS 2020 - 8th International Conference on Sport Sciences Research and Technology Support
36

7 FUTURE WORK
For YouTube, all 10 clips were successfully identi-
fied, which shows that the models trained with SVM
worked properly, although the number of YouTube
clips is still small. Since the number of data is lim-
ited, we need to confirm the generality using a large
amount of data. Also, the robustness of the identifi-
cation should be verified, because other noise sources
will be mixed into the input sound, and the distance
between a microphone and a sound source can not
be well controlled in practice, and the deference of
experiment place and weather. Future work also in-
cludes an extension of the proposed method to esti-
mate more information such as the number of revolu-
tions and the ball speed.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
No. 19K12017, 19KK0260 and 20H00475.
REFERENCES
Appelbaum, L. G. and Erickson, G. (2018). Sports vi-
sion training: A review of the state-of-the-art in digital
training techniques. International Review of Sport and
Exercise Psychology, 11(1):160–189.
Baodon, Y. (2014). Hawkeye technology using tennis
match. Computer Modelling & New Technologies,
18(12):400–402.
Canal-Bruland, R. (2018). Auditory contributions to visual
anticipation in tennis. Psychology of Sport and Exer-
cise, 36:100–103.
Cao, Z., Hidalgo Martinez, G., Simon, T., Wei, S., and
Sheikh, Y. A. (2019). OpenPose: Realtime multi-
person 2D pose estimation using part affinity fields.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, pages 1–1.
Cust, E. E., Sweeting, A. J., Ball, K., and Robertson, S.
(2019). Machine and deep learning for sport-specific
movement recognition: a systematic review of model
development and performance. Journal of Sports Sci-
ences, 37(5):568–600.
Diamantaras, K. I. and Kung, S. Y. (1998). Principal com-
pornent neural networks: Theory and applications. In
Karhunen, J., editor, Pattern Analysis and Applica-
tions, pages 74–75. John Wiley & Sons.
Kogusuri, Y., Sato, T., Toyoda, K., and Miyato, S. (2008).
Developement of the holding judgement technology
using batted ball sound of sound table tennis. The
Proceeding of the Conference on Information, Intel-
ligence and Precision Equipement : IIP, (8):49–52.
Okamoto, H., Moro, A., Yamashita, A., and Asama, H.
(2015). Toward sports training service with the in-
teractive learning platform. In Sawatani, Y., Spohrer,
J. C., Kwan, S. K., and Takenaka, T., editors, Service-
ology for Smart Service System, Selected papers of the
3rd International Conference of Serviceology, ICServ
2015, San Jose, CA, USA, 7-9 July 2015, pages 231–
236. Springer.
Playsight (2020). Smartcourt. https://www.playsight.com.
Scholkopf, B., Burges, C. J. C., and Smola, A. J. (1999). In
Advances in Kernel Methods - Support Vector Learn-
ing. The MIT Press, USA.
SecondSpetrum (2020). The next way of seeing sports.
https://www.secondspectrum.com/index.html.
Seo, S.-W., Kim, M., and Kim, Y. (2018). Optical and
acoustic sensor-based 3d ball motion estimation for
ball sport simulators. Proceedings of the 2017 Inter-
national Conference on Information and Communica-
tion Technology Convergence, 18(1323).
Vapnik, V. N. (1998). In Statistical Learning Theory. John
Wiley and Sons.
Zepp (2020). Smart tennis sensors. https://www.
secondspectrum.com/index.html.
Zhang, D., Yokohama, K., and Yamamoto, Y. (2017). Char-
acterisitics of impact sound in tennis service among
top-level players. Nogoya J. Health, Physical, Fit-
tness, Sports, 40(1):37–43.
Detection of Ball Spin Direction using Hitting Sound in Tennis
37
