Validating Results of 3D Finite Element Simulation for Mechanical

Stress Evaluation using Machine Learning Techniques

Alexander Smirnov

, Nikolay Shilov

, Andrew Ponomarev

Thilo Streichert

, Silvia Gramling

and Thomas Streich

SPIIRAS, 14

Line, 39, St. Petersburg, Russia

ITMO University, Kronverksky pr., 49, St. Petersburg, Russia

Festo SE & Co. KG, Ruiter Str., 82, Esslingen, Germany

Keywords: Artificial Intelligence, 3D Simulation Data, Mechanical Stress Evaluation, Geometric Features, Resnet18,

VoxNet.

Abstract: When a new mechanical part is designed its configuration has to be tested for durability in different usage

conditions (‘stress evaluation’). Before real test samples are produced, the model is checked analytically via

3D Finite Element Simulation. Even though the simulation produces good results, in certain conditions these

could be unreliable. As a result, validation of simulation results is currently a task for experts. However, this

task is time-consuming and significantly depends on experts’ competence. To reduce the manual checking

effort and avoid possible mistakes, machine learning methods are proposed to perform automatic pre-sorting.

The paper compares several approaches to solve the problem: (i) machine learning approach, relying on

geometric feature engineering, (ii) 2D convolutional neural networks, and (iii) 3D convolutional neural

networks. The results show that usage of neural networks can successfully classify the samples of the given

training set.

1 INTRODUCTION

When a new mechanical part is designed, it has to be

tested for durability in different usage conditions

(‘stress evaluation’). In order to save on time and

expenses, the model is usually checked analytically

before real test samples are produced. However,

automated simulations sometimes deliver results that

require expert knowledge for interpretation.

Currently, experts validate if the results are reliable

and detect the nonreliable ones (fig. 1, a). This is a

time-consuming and prone to errors process.

In case of finite element simulations (Reddy,

2009), nonreliable results (“failures”) can arise from,

for example:

 Overlapping components in the imported CAD

file,

 Contact of different (rigid) components or

https://orcid.org/0000-0001-8364-073X

https://orcid.org/0000-0002-9264-9127

https://orcid.org/0000-0002-9380-5064

https://orcid.org/0000-0002-8197-3538

https://orcid.org/0000-0002-0191-6366

 Equal treatment of tensile and compressive stress.

In order to reduce the manual checking efforts and

also to avoid checking mistakes, training of machine

learning models that allow automatic pre-sorting is

proposed within the scope of this research study (fig.

1, b).

The challenge of this classification task is that the

simulation results are given as unstructured 3D point

clouds, so common frameworks for processing

regular data, e.g. for image recognition, cannot be

applied directly. That is why different problem

specific approaches have to be studied.

The research question considered in the paper is if

the classification of reliability (automated validation)

of the 3D finite element simulation results can be

done using AI and which AI approaches can provide

for acceptable results.

The paper compares three approaches to solve the

Smirnov, A., Shilov, N., Ponomarev, A., Streichert, T., Gramling, S. and Streich, T.

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques.

DOI: 10.5220/0010108500130023

In Proceedings of the International Conference on Innovative Intelligent Industrial Production and Logistics (IN4PL 2020), pages 13-23

ISBN: 978-989-758-476-3

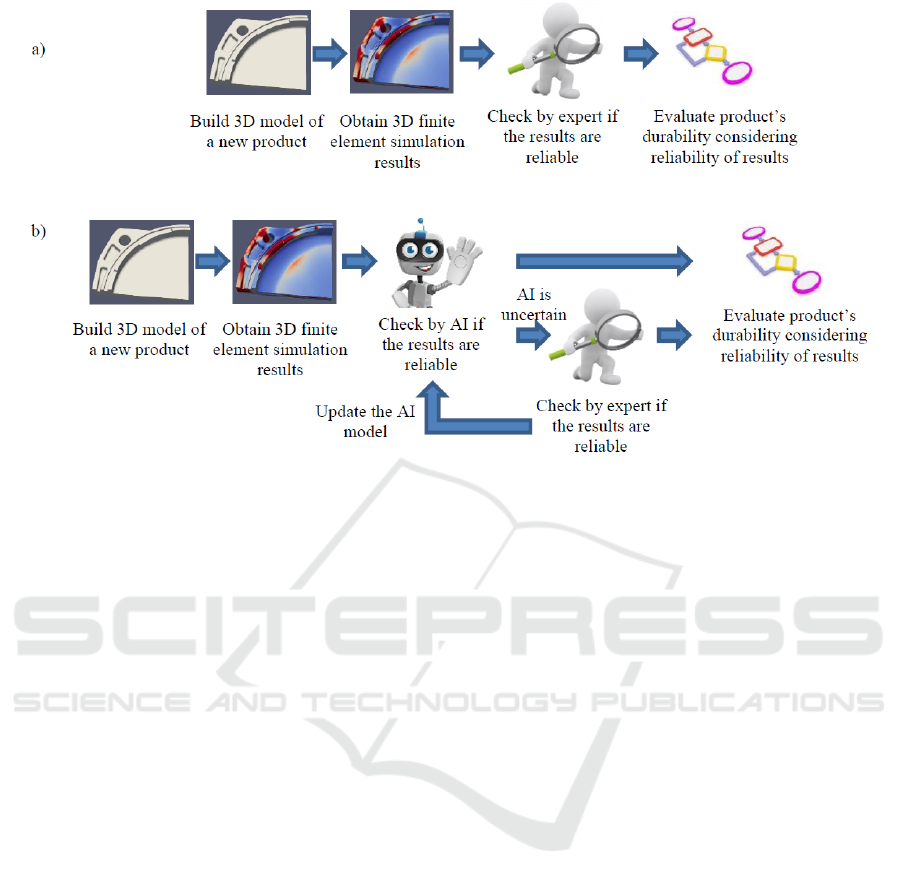
Figure 1: The process of evaluating new product’s durability: current (a), desired (b).

problem using different machine learning techniques:

1) machine learning approach, relying on geometrical

feature engineering, 2) 2D convolutional neural

networks, and 3) 3D convolutional neural networks.

The paper is strucutred as follows. The next

section defines the problem at hand. It is followed by

the state of the art review. Sections 4-6 repesent the

AI training and classification results for the above

mentioned techniques. The results are compared and

discussed in section 7. The conclusions summarize

the findings and outline the future research directions.

2 PROBLEM DEFINITION

The source data for the classification problem is

stored in VTU mesh files (Kitware Inc., 2005) with

different number of points per inch depending on the

curvature of a particular fragment of the model (less

points on smooth surfaces and more points for

curves). An average number of vertices in a model is

around 5000 but it differs significantly from model to

model. Due to symmetry, models are given as 1/4 part

or 1/2 part of a component. If the components had no

symmetry properties, the model would have

represented the whole part.

The locations of the vertices of a sample are set

before the simulation is conducted. The output of the

simulation are so-called safety factor values for each

vertex. This safety factor (SF) value is defined as the

relationship between an allowable mechanical load

and a given mechanical load. That means, the higher

the SF, the more stable the simulated component is.

That is why the SF is used as a metric to decide if a

component fulfils the mechanical requirements of the

development process. Therefore, the minimal SF

value has to lie above a certain threshold. Validation of

the reliability of this minimal SF is the problem at

hand. In order to automate it, within the scope of this

research work machine learning models have been

developed to validate if this minimum is reliable or not.

The reliability check is then applied iteratively: If the

global minimum is not reliable, the second lowest local

minimum is validated and so on until a reliable

minimum is found. This SF minimum has to lie above

the threshold to be mechanically stable. Otherwise, the

construction needs to be re-engineered.

In the dataset of this research study, the label

refers to the global minimum, so only the global

minimum is classified. Since the global minimum is

the easiest to find and the patterns for classification

are the same for other local minima, this study is

focused on the classification of the global minimum.

The the test set consisting of 814 simulation

results was manually classified by an expert based on

the evaluation of the reliability of the global

minimum so that 304 samples were considered as

reliable (“reliable samples”), and 510 samples as

nonreliable (“nonreliable samples”). The nonreliable

samples are split into 3 types of failures (failure

modes): 142, 115, and 253 samples respectively.

However, in the presented research only two labels are

IN4PL 2020 - International Conference on Innovative Intelligent Industrial Production and Logistics

used: reliable and unreliable. Classification of samples

into failure modes is still the subject of future research.

3 STATE-OF-THE-ART REVIEW

The considered task is rather unique, and no “of the

box” solutions or methods have been found. As a

result, the paper presents approaches for classifying

models of 3D objects. One can read on advances in

3D object classification in (Ahmed et al., 2018;

Ioannidou et al., 2017). Based on these, all

approaches to 3D object classification can be split

into the following groups:

 Architectures exploiting descriptors extracted

from 3D data,

 Architectures exploiting RGB data,

 Architectures exploiting 3D data directly.

The first group of approaches is not directly

related to 3D object classification but follows the

generic approach of feature selection and application

of various models to the features and their

combinations (L. Ma et al., 2018; Wahl et al., 2003).

These models are less computationally expensive and

are preferable for tasks where they can be applied

successfully. However, they often cannot work well

for distinguishing between some complex shapes.

The second group of approaches is based on

application of various techniques to generating 2D

images out of 3D objects and their further

classification. These approaches can also be split into

two groups: (i) analysing various views, projections,

and cuts, and (ii) analysing images with depth

information. The advantage of these approaches is the

possibility to use well-studied 2D classification

techniques without the need to develop a new 3D

model. However, extensive application of such

techniques caused appearance of specialized multi-

view models (Su et al., 2015; Yavartanoo et al., 2019;

Zhou et al., 2020). The cut-based approaches are most

often used in medical domain since many medical

data, for example, tomography results, were

originally represented as cuts (Deng et al., 2018; Lu

et al., 2018; Z. Ma et al., 2018), however they are

applied in other domains as well (Qiao et al., 2018).

Analysing images with depth information (often

referred as RGB-D) is a very popular group of

approaches. They also had the advantage of applying

state-of-the-art 2D classification techniques to

classifying 3D objects but developed into a separate

group classification models (Feng et al., 2016;

Schwarz et al., 2015).

Direct analysis of 3D data can also be approached

from different perspectives. Classification of meshes

(Hanocka et al., 2019) and irregular point clouds

(Charles et al., 2017; Y. Wang et al., 2019) are

characterized by speed and absence of the need of

computation-intensive pre-processing since usually

engineering and design data (e.g., CAD models) are

stored in this form. Approaches based on analysis of

regular point clouds (voxel-based models) provide

better results “out-of-the-box”, for the price of

additional data pre-processing (Maturana & Scherer,

2015).

In the presented research one approach from each

group was tested: classification based on geometrical

feature engineering, 2D convolutional neural network

(Resnet18) for depth images, and 3D convolutional

neural network VoxNet. A number of models for

irregular point clouds have also been tested, but so far

their result were much worse than those presented so

they are not considered in the paper.

4 CLASSIFICATION BASED ON

GEOMETRIC FEATURES

4.1 Approach Description

The first approach is to build a classification model

that relies on geometrical feature engineering. As the

definition of the error modes is connected to some

geometric properties of the SF minimum point and its

neighbourhood, a set of features was proposed

describing the geometry of the neighbourhood of the

SF minimum. In particular, the features describe the

complexity of the SF minimum neighbourhood,

including two interpretations of mesh complexity:

1. Structural complexity, related to the number of

nodes and faces in the mesh.

2. Geometric complexity, describing how similar the

surface is to a “simple” shape (e.g., plane).

Structural complexity is quite easy to formalize

and evaluate. We created two groups of features:

cells_no_X (number of mesh cells in the SF minimum

neighbourhood of the given radius in millimetres) and

points_no_X (number of mesh nodes in the SF

minimum neighbourhood of the given radius in

millimetres). The corresponding features are

calculated by intersecting the input mesh with a

sphere of the particular radius positioned to the SF

minimum point and finding the properties of the

resulting mesh.

It is not clear in advance what is the size of the SF

neighbourhood that is the most informative to the

reliability classification. In order to understand that,

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques

each feature was generated w.r.t. different sizes of

neighbourhood (sphere radiuses). For example, we

created the features “number of nodes in 1 mm radius

neighbourhood” (points_no_1), as well as in 2 mm

(points_no_2), 3 mm (points_no_3) radius

neighbourhoods and so on. It applies to all the

features (representing both structural and geometric

complexity).

The notion of geometric complexity is not so

straightforward to formalize. Therefore, several

features were introduced.

The first is the volume of the minimal oriented

bounding box of the neighbourhood of the specified

size (obb_volume_X). The intuition behind this

feature is that flat or slightly bent surfaces have a

bounding box with zero or close to zero volume,

while for curved surfaces the bounding box will be

(almost) close to a cube having relatively large

volume. Minimal oriented bounding boxes are

estimated with a help of trimesh library (Dawson-

Haggerty et al., n.d.).

The second group of features is generalized

variance of face normals (in the neighbourhood of the

specified size – gen_var_X), estimated according to

the following formula:











||





















where  – a set of vectors normal to mesh faces (each

vector is 3-dimensional), and 



– is the mean normal.

The next group of features is the neighbourhood

convexity, estimated using the tangent plane,

containing the minimum SF point. In particular, there

are two groups of features, calculated using this tangent

plane. Features convexity1_X are defined as the mean

value of the plane equation for the neighbourhood

points, while convexity2_X features are defined as the

logarithm of the ratio of the number of points in the

positive subspace w.r.t. the tangent plane, to the

number of points in the negative subspace.

The features of the next group are rooted in the

notion of surface curvature. Specifically, we use the

notion of discrete gaussian curvature measure as

defined in (Cohen-Steiner & Morvan, 2003) and

implemented in trimesh library. This gives two

groups of features gauss_curv_X (the sum of the

discrete gaussian curvature of the nodes in the

specified neighbourhood) and gauss_curv_avgd_X

(mean discrete gaussian curvature of the specified

neighbourhood).

All the described groups of features characterize

the SF minimum neighbourhood of the given size in

millimetres. The last group of features describe the

closest possible neighbourhood of the SF minimum

node, given by the mesh structure – nodes reachable

from the SF minimum by one and two ‘hops’. This

gives features edgeness_min_1nbr,

edgeness_max_1nbr, edgeness_min_2nbr, and

edgeness_max_2nbr. In the name of these features

min and max correspond to minimal and maximal

values of the cosine of the angle between the normal

of faces situated in the given neighbourhood, and

1nbr and 2nbr suffixes correspond to the

neighbourhoods reachable in one and two hops from

the minimum SF point respectively. The complete list

of features is provided in the table 1.

4.2 Feature Importance Analysis

Feature importance analysis shows how informative

each feature is in the process of classification. In this

problem, the role of feature importance analysis is at

least twofold:

1. The features are very similar, they all try to

capture convexity in some sense. Which one is

better?

2. What neighbourhood size is the most

informative? This knowledge can help to keep the

model small and thus to speed up the processing.

Besides, understanding the size of the informative

neighbourhood may help to select

neighbourhoods used to train other ML methods.

Table 1: The list of features.

Feature Neighbourhood sizes, mm

cells_no_X 10, 8, 6, 5, 4, 3, 2, 1

points_no_X 10, 8, 6, 5, 4, 3, 2, 1

obb_volume_X 10, 8, 6, 5, 4, 3, 2, 1

gen_var_X 10, 8, 6, 5, 4, 3, 2, 1

convexity1_X 5, 4, 3, 2, 1

convexity2_X 5, 4, 3, 2, 1

gauss_curv_X 5, 4, 3, 2, 1

gauss_curv_avgd_X 5, 4, 3, 2, 1

edgeness_min_1nbr -

edgeness_max_1nbr -

edgeness_min_2nbr -

edgeness_max_2nbr -

To estimate feature importance we used null

importance method (Altmann et al., 2010; Grellier,

2018) in conjunction with feature importance

estimation procedures typical for the tree-based

learning algorithms.

The idea is as follows. The machine learning

algorithm leveraged for reliability classification is a

decision tree-based gradient boosting implemented in

CatBoost library (Yandex, 2020b). Decision tree-

based learning algorithms have an internal ability to

IN4PL 2020 - International Conference on Innovative Intelligent Industrial Production and Logistics

estimate feature importance, i.e. the impurity measure

(information or Gini) gain, which is obtained by the

splits that use the particular feature (Y. Y. Wang &

Li, 2008). Gradient boosting on decision trees

implemented in CatBoost is not an exception, as it

also estimates the importance of the input features by

how on average the prediction changes if the feature

value changes (Yandex, 2020a). However, feature

importance estimation is not always indicative of the

actual importance of the feature, especially in

multidimensional spaces and in the presence of noise.

The main problem is that it is usually is not clear what

level of impurity gain corresponds to some real

patterns in the data, and what gain can be learned even

from the noise.

The null importance method provides some kind

of a ‘reference point’ in assessing the importance. The

rationale behind the method is following. Let’s

consider a slightly modified learning dataset, where

feature f is replaced with its random permutation f*.

A learning algorithm can be applied to the modified

dataset and an importance of f* can be estimated in a

usual way. Further, as we repeat this process several

times, for each feature we can build an importance

distribution (null importance distribution). That

distribution essentially provides the required

‘reference point’ – if sampling the importance of the

feature f in its original ordering is likely to be sampled

from this distribution then the feature is actually no

more important than the random noise. On the other

hand, if the importance of the feature in its original

ordering is greater than the importance of most of the

permutations of this feature, it actually carries some

information about the target. This also gives a way to

measure the importance, e.g., by considering the ratio

of the importance of the original feature ordering to

the 3rd quartile of the null importance distribution.

Table 2 shows top 10 features estimated by the

described procedure. It can be seen from the table that

Table 2: Top 10 features according to the null importance

method.

Feature Importance

convexity1_4 5.5

convexity1_3 4.6

convexity1_5 4.0

convexity2_4 3.8

convexity2_3 3.8

convexity2_5 2.2

obb_volume_2 1.8

gauss_curv_avgd_2 1.3

convexity2_2 0.97

convexity2_1 0.95

only 5 features have importance greater than the 3

quartile of the null importance distribution. The most

important features are various convexity indicators

applied to the SF minimum neighbourhoods of the

radius 3 mm and 4 mm. Smaller and larger

neighbourhoods are not so important.

5 CNN-BASED CLASSIFICATION

OF DEPTH IMAGES

The second approach is based on the representation

of the 3D models as 2D depth images and further

classification by a convolutional neural network. In

certain sense this representation can be considered as

surface model, where coordinates of an image point

correspond to the coordinates of the surface point

along two axes, and the depth colour can be

considered as the coordinate along the third axis.

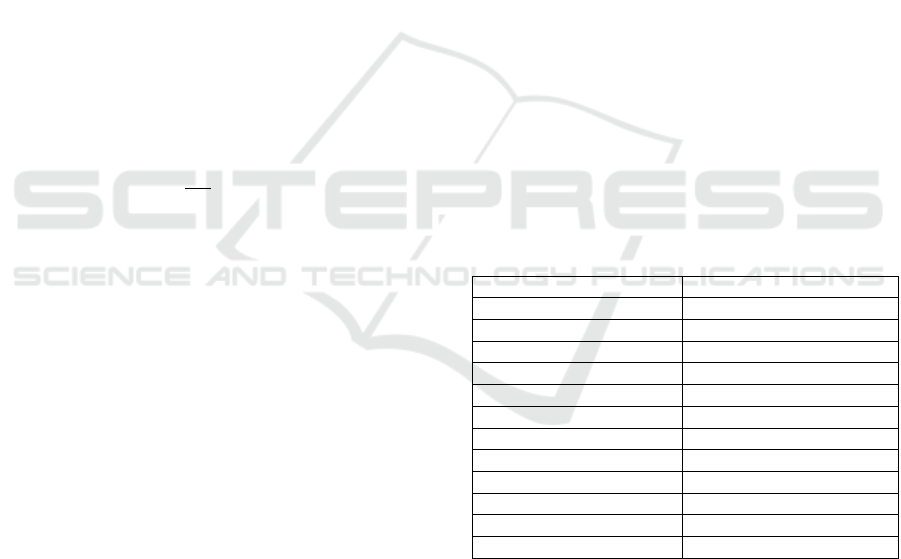
Generation of the depth images has been done via

the following procedure. First, the fragment of a

given diameter around the analysed point (the point

with the minimal SF, fig. 2, a and b). Experiments

were carried out with radiuses of 2, 3, and 4 mm,

however for simplicity 3 mm radius is considered in

the descriptions below.

Then, the fragment is rotated so that the normal of

the analysed point would be oriented along axis Z

(pointing to the viewer in fig. 2, c).

In the presented example, one can see that in some

complex shapes, there can be fragments obstructing

the analysed point, and, as a result, it is not possible

to see the shape around it. For this purpose, a

procedure has been developed for removing such

obstructing fragments. It consists of two steps:

(1) remove all points whose normals are oriented to

opposite direction (cosine between the normals of

analysed point and checked point is negative);

(2) remove all fragments that are not connected to the

fragment containing the analysed point. The resulting

fragment is shown in fig. 2, d.

Finally, the depth map is built via measuring

distances between the fragment and nodes of a

224x224 grid located on a flat surface, which is

perpendicular to the normal of the analysed minimum

and positioned 3 mm away from it (fig. 3). The closer

points are lighter (the points located 0 mm away from

the grid are white), and the further points are darker

(the points located 6 mm away from the grid are

black). The resulting image is shown in fig. 2, e.

Since CNNs are usually oriented to object

recognition, they do not work very well with colour

shades, but with borders. For this reason, the contrast

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques

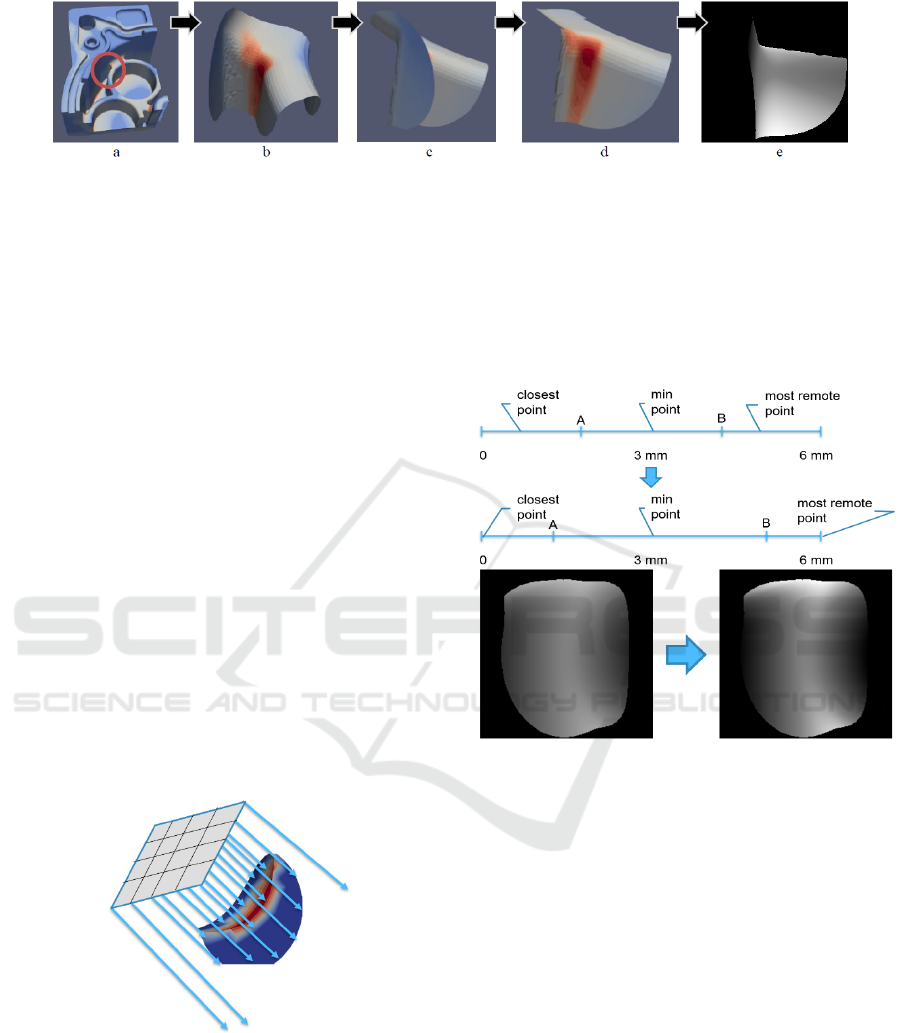
Figure 2: The process of generating depth image of 3D model.

of the generated images was increased. However, it

was done in such a way that the analysed point always

coloured as 127 (“located” 3 mm away from the grid).

At the same time closer and further parts are

“zoomed” proportionally to the closest and furthers

points (fig. 4). We understand that the procedure of

increasing contrast produces a risk of losing

information about curvature, however, this was not a

case for the considered training set.

Resnet18 was chosen as a classification model.

Resnet18 is a 18 layers deep residual CNN for image

classification (He et al., 2016). Experimentation

showed that usage of pre-trained network did not give

any advantage during training, so the network with

randomly initialised weights was used. The following

training parameters were applied for training:

 Additional linear layer was added with sigmoid

output at the network output for binary

classification;

 Error function: cross entropy;

 Used augmentations (for training set only) are

horizontal flip and 15 rotations by 22,5 degrees

(31 augmentations for each sample);

 Learning rate 1.0e-6 (no learning rate degrading);

 Batch size: 32.

Figure 3: Measuring distance between a surface and 3D

object.

The network was implemented in TorchVision

library (Facebook Inc., 2020) ver. 0.6.0. One training

procedure (1 fold and 50 epochs) on the Intel Xeon

server with Nvidia Geforce 2080 RTX GPU took

about 35 minutes. The training results are presented

in fig. 5-7.

For the comparison with other techniques, the

following numbers of epochs have been chosen for

each of the radius that let one to avoid overfitting:

2 mm – 20 epochs (no more significant

improvement), 3 mm – 14 epochs (further training

causes overfitting), and 4 mm – 8 epochs (further

training causes overfitting).

Figure 4: Increasing the contrast of depth images.

One can see that classification of samples with the

radius of 2 mm produces the best results, however,

there is a concern that in the future analysing such

small fragments of the parts can produce false results.

On the other side, fragments with the radius of 4

mm are not classified well and the model becomes

overfitted already after 10 epochs, with the loss

function values being higher than those for smaller

fragments. As a result, for future research the

classification of fragments with radiuses of 2 and 3

mm were selected.

6 3D CNN-BASED

CLASSIFICATION OF

VOXELIZED MODELS

The third implemented model is an adaptation of a 3D

CNN to the reliability classification problem. The

IN4PL 2020 - International Conference on Innovative Intelligent Industrial Production and Logistics

Figure 5: Training results of Resnet18-based depth image classification of 2 mm radius fragments.

Figure 6: Training results of Resnet18-based depth image classification of 3 mm radius fragments.

rationale is that two-dimensional representation (even

with the depth map) misses some details of the part

(e.g., it cannot distinguish between solid and hollow

parts), and 3D model makes the difference between

the inside and outside of the part more obvious. It is

self-evident, that 3D representation contains much

more detail about an object. The reason why neural

networks for processing 3D data receive relatively less

attention is that in most cases there are just no accurate

3D data. For example, in object detection problem, 3D

representation typically should be constructed from 2D

data or LiDAR data and this reconstruction is a

problem itself. However, in the area of manufacturing

(CAD/CAM systems) precise 3D models are available,

which makes 3D neural networks (and 3D CNN, in

particular) a reasonable choice.

We have adapted VoxNet architecture described in

(Maturana & Scherer, 2015). Original VoxNet is

designed for object recognition problem and has

softmax output layer (with the number of output units

equal to the number of classes of objects). As

reliability classification is binary classification

problem, we changed the softmax output layer to a

dense layer consisting of one unit with sigmoid

activation function. We used the same input size as

the

original

model:

32x32x32

(fig.

8). Overall,

the

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques

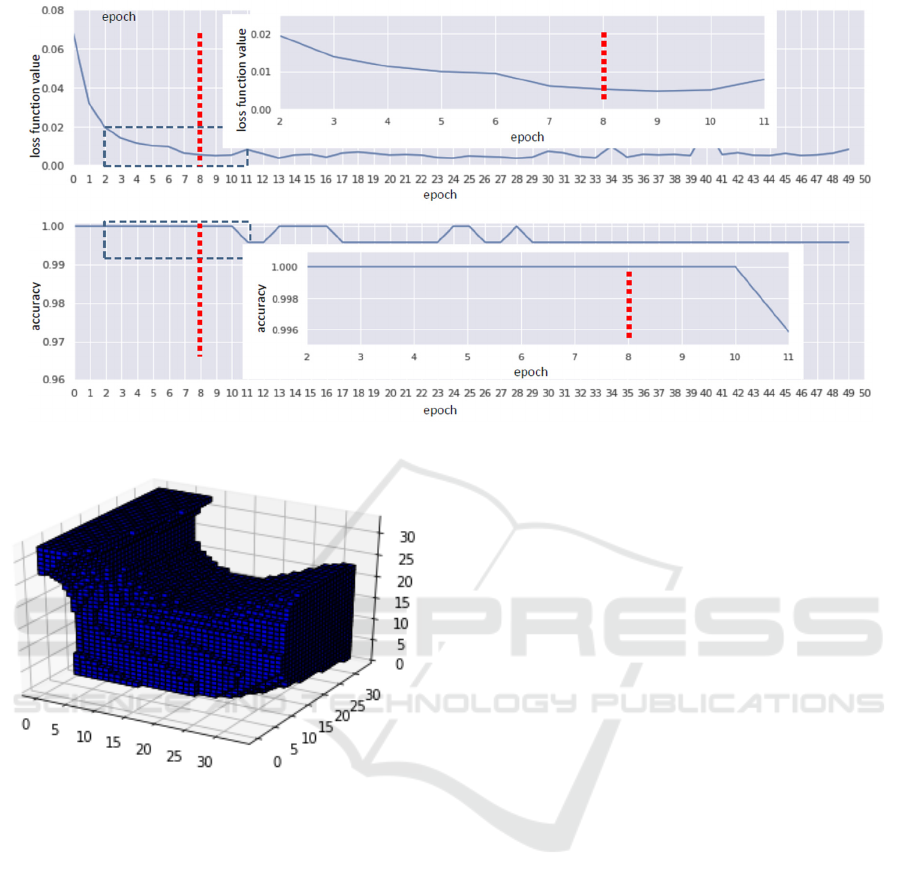
Figure 7: Training results of Resnet18-based depth image classification of 4 mm radius fragments.

Figure 8: Example of a voxelized neighbourhood of a SF

minimum.

adapted VoxNet implementation has the following

structure:

3D convolution layer with filter size 5, strides 2,

normal padding and Leaky ReLU activation

function with alpha 0.1.

2. 3D convolution layer with filter size 3, strides 1,

normal padding and Leaky ReLU activation

function with alpha 0.1.

3. 3D max pooling layer with pool size 2 and strides

4. Reshape to flat vector (of size 6*6*6*32).

5. Dense layer with 128 units and ReLU activation.

6. Dense output unit with sigmoid activation.

The network is trained with the Adam algorithm

for minimization of binary cross-entropy as a loss

function.

The data preparation procedure is the following.

The part model is rotated to align the direction of the

normal at the point of the examined SF minimum with

Z axis. Then, the neighbourhood of the examined SF

minimum node is transformed into a voxel model

32x32x32 so that the minimum SF point corresponds

to the centre of the cube (voxel with coordinates [17;

17; 17]). The size of each voxel is 0.1 mm

, therefore,

a whole voxelized neighbourhood has dimensions

3.2x3.2x3.2 mm. An example of a pre-processed

network input is shown in fig. 8. While the position

of the normal at SF minimum is determined by the

pre-processing step, the part may still be rotated

around Z axis resulting in different models and

potentially different results. To achieve the invariance

to this rotations, we used an augmentation scheme,

according during the training voxelization of 16

rotations of each model around Z axis were

considered, and for each rotation, also one flipping.

Therefore, each SF minimum point results in 32

training samples.

7 EVALUATION AND

COMPARISON

The dataset contains 814 mesh models (samples) with

SF assigned to each vertex of the mesh. Sample label

in the dataset is determined by the expert

classification of the node with the lowest SF (global

minimum) reliability. The dataset contains 304

samples with reliable global minimum and 510

samples with non-reliable global minimum.

IN4PL 2020 - International Conference on Innovative Intelligent Industrial Production and Logistics

To evaluate the classification algorithms, the k-

fold cross-validation procedure has been carried out.

In accordance with this procedure, the data set is

divided into k subsets of approximately equal size,

and k experiments are performed so that each of the k

subsets is used once as the test set and the other k-1

subsets are put together to form the train set. In our

case the dataset has been split into 5 folds (k=5). The

resulting train and test sets are presented in Table 3.

During splitting the dataset, the following

consideration was taken into account. Not all models

of the dataset correspond to different components but

to result of a different simulations, i.e. a different

mechanical load case. As a result, some samples may

correspond to the same component but have different

SF values and different vertices with minimal SFs.

This fact was taken into account during splitting. It

turned out that different simulations of the same part

tend to place minimum SF to similar locations of the

part. Therefore, to prevent overfitting to a particular

part, the folds were created in such a way, that the

same part does not present both in the train and test

sets (sometimes, this is referred to as “group K-fold

validation”; in this case, the group is interpreted as

simulation results of one component).

The described above algorithms have been

evaluated on the same set of folds. They include

(1) CatBoost with all features, (2) CatBoost with top

10 features, (3-5) Resnet18 for neighborhoods with

radiuses of 2 mm, 3 mm, and 4 mm, and (6) VoxNet.

We have also added the logistic regression as a base

classification model for the comparison.

To evaluate the algorithms two types of criteria

were considered: performance, measured by training

and prediction times; and prediction quality,

measured by accuracy. However, it turned out that the

accuracy values were quite high, so the absolute

number of misclassified samples was also considered

(it does not provide additional information compared

to the accuracy, but slightly easier to read and

interpret). The results of the evaluation are shown in

Table 4.

It can be seen, that all the models achieve quite

good results in terms of accuracy. Logistic regression

has a significant advantage in training time over the

other models, but has the lowest accuracy. Taking

into account, that training is not so frequent operation

in the intended use cases of the model, and training

times of deep learning models are also reasonable,

this advantage is not very important. None of the

explored feature-based models were able to achieve

perfect classification, which is most likely related to

the fact that proposed features didn’t describe

significant aspects of the SF minimum

neighbourhood necessary for such classification.

Among

the deep learning-based models, 3D CNN

Table 3: Distribution of samples for folds used in the experiment.

Fold

Train set Test set

“Reliable”

samples

“Unreliable”

samples

Total

“Reliable”

samples

“Unreliable”

samples

Total

1 258 391 649 46 119 165

2 212 437 649 92 73 165

3 246 405 651 58 105 163

4 252 401 653 52 109 161

5 248 406 654 56 104 160

Table 4: Comparison of approaches to Validating Results of 3D Finite Element Simulation.

Classification

approach

Errors on fold

Mean training time, s

Mean prediction

time, s

Mean accuracy

Mean # of

errors

1 2 3 4 5

Logistic regression 2 1 0 0 10 0.017 0.006 0.984 2.6

CatBoost 0 4 0 0 0 1.58 0.008 0.995 0.8

CatBoost

(10 features)

0 2 2 2 0 0.988 0.007 0.993 1.2

Resnet18 (radius

0 0 0 0 0

800 (GPU, 20

epochs)

0.036

(no GPU)

1 0

Resnet18 (radius

0 0 0 0 0

560 (GPU, 14

epochs)

0.036

(no GPU)

1 0

Resnet18 (radius

0 0 0 0 0 320 (GPU, 8 epochs)

0.036

(no GPU)

1 0

VoxNet 0 0 0 0 0 9.6 (GPU, 3 epochs) 0.161 1 0

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques

VoxNet can be considered the best, as it achieves

perfect classification of the provided dataset and has

significantly lower training time than other models. It

supports the initial intuition that 3D CNN should be a

reasonable choice as they fully exploit the 3D

structure of analysed components.

Based on the results, it was decided that further

research should focus on the Resnet18 models for the

radius of 2 and 3 mm and the VoxNet model.

8 CONCLUSIONS

The paper is aimed at application of AI techniques to

reliability evaluation of 3D simulation results

produced via 3D finite element simulation. It was

found that such classification is possible by various

3D model classification techniques, and some of them

produce perfectly accurate results.

Among the machine learning approach, relying on

geometrical features, 2D depth image classification

via Resnet18, and VoxNet-based classification of

voxelized models, the latter two were selected for

further analysis.

Future research is planned to be aimed for two

major aspects. First, currently only global SF minima

were classified, whereas in reality, local minima need

to be classified as well.

Second, absolute sizes of components (and

component fragments) were used for classification.

However, there can be components with significantly

different sizes and the appropriate sample radius may

differ from the findings in this paper. Approaches to

either scale models or choose the fragments according

to the number of included vertices need to be studied,

which might be more generic for varying component

sizes.

ACKNOWLEDGEMENTS

The paper is due to collaboration between SPIIRAS

and Festo SE & Co. KG. The state-of-the-art analysis

(sec. 3) is due to the grant of the Government of

Russian Federation (grant 08-08). The CNN-based

classification (sec. 5) is partially due to the State

Research, project number 0073-2019-0005.

REFERENCES

Ahmed, E., Saint, A., Shabayek, A. E. R., Cherenkova, K.,

Das, R., Gusev, G., Aouada, D., & Ottersten, B. (2018).

A survey on Deep Learning Advances on Different 3D

Data Representations. http://arxiv.org/abs/1808.01462

Altmann, A., Toloşi, L., Sander, O., & Lengauer, T. (2010).

Permutation importance: a corrected feature importance

measure. Bioinformatics, 26(10), 1340–1347.

https://doi.org/10.1093/bioinformatics/btq134

Charles, R. Q., Su, H., Kaichun, M., & Guibas, L. J. (2017).

PointNet: Deep Learning on Point Sets for 3D

Classification and Segmentation. 2017 IEEE

Conference on Computer Vision and Pattern

Recognition (CVPR), 77–85.

https://doi.org/10.1109/CVPR.2017.16

Cohen-Steiner, D., & Morvan, J.-M. (2003). Restricted

delaunay triangulations and normal cycle. Proceedings

of the Nineteenth Conference on Computational

Geometry - SCG ’03, 312.

https://doi.org/10.1145/777792.777839

Dawson-Haggerty et al. (n.d.). trimesh.

Deng, X., Zheng, Y., Xu, Y., Xi, X., Li, N., & Yin, Y.

(2018). Graph cut based automatic aorta segmentation

with an adaptive smoothness constraint in 3D

abdominal CT images. Neurocomputing, 310, 46–58.

https://doi.org/10.1016/j.neucom.2018.05.019

Facebook Inc. (2020). PyTorch. https://pytorch.org/

Feng, J., Wang, Y., & Chang, S.-F. (2016). 3D shape

retrieval using a single depth image from low-cost

sensors. 2016 IEEE Winter Conference on Applications

of Computer Vision (WACV), 1–9.

https://doi.org/10.1109/WACV.2016.7477652

Grellier, O. (2018). Feature Selection With Null

Importances.

Hanocka, R., Hertz, A., Fish, N., Giryes, R., Fleishman, S.,

& Cohen-Or, D. (2019). MeshCNN: A Network with an

Edge. ACM Transactions on Graphics, 38(4), 1–12.

https://doi.org/10.1145/3306346.3322959

He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual

Learning for Image Recognition. 2016 IEEE

Conference on Computer Vision and Pattern

Recognition (CVPR), 770–778.

https://doi.org/10.1109/CVPR.2016.90

Ioannidou, A., Chatzilari, E., Nikolopoulos, S., &

Kompatsiaris, I. (2017). Deep Learning Advances in

Computer Vision with 3D Data. ACM Computing

Surveys, 50(2), 1–38. https://doi.org/10.1145/3042064

Kitware Inc. (2005). File Formats for VTK Version 4.2.

https://vtk.org/wp-content/uploads/2015/04/file-

formats.pdf

Lu, X., Xie, Q., Zha, Y., & Wang, D. (2018). Fully

automatic liver segmentation combining multi-

dimensional graph cut with shape information in 3D CT

images. Scientific Reports, 8(1), 10700.

https://doi.org/10.1038/s41598-018-28787-y

Ma, L., Sacks, R., Kattel, U., & Bloch, T. (2018). 3D Object

Classification Using Geometric Features and Pairwise

Relationships. Computer-Aided Civil and

Infrastructure Engineering, 33(2), 152–164.

https://doi.org/10.1111/mice.12336

Ma, Z., Wu, X., Song, Q., Luo, Y., Wang, Y., & Zhou, J.

(2018). Automated nasopharyngeal carcinoma

segmentation in magnetic resonance images by

IN4PL 2020 - International Conference on Innovative Intelligent Industrial Production and Logistics

combination of convolutional neural networks and

graph cut. Experimental and Therapeutic Medicine.

https://doi.org/10.3892/etm.2018.6478

Maturana, D., & Scherer, S. (2015). VoxNet: A 3D

Convolutional Neural Network for real-time object

recognition. 2015 IEEE/RSJ International Conference

on Intelligent Robots and Systems (IROS), 922–928.

https://doi.org/10.1109/IROS.2015.7353481

Qiao, K., Zeng, L., Chen, J., Hai, J., & Yan, B. (2018). Wire

segmentation for printed circuit board using deep

convolutional neural network and graph cut model. IET

Image Processing, 12(5), 793–800.

https://doi.org/10.1049/iet-ipr.2017.1208

Reddy, J. N. (2009). An Introduction to the Finite Element

Method (3rd ed.). McGraw-Hill.

Schwarz, M., Schulz, H., & Behnke, S. (2015). RGB-D

object recognition and pose estimation based on pre-

trained convolutional neural network features. 2015

IEEE International Conference on Robotics and

Automation (ICRA), 1329–1335.

https://doi.org/10.1109/ICRA.2015.7139363

Su, H., Maji, S., Kalogerakis, E., & Learned-Miller, E.

(2015). Multi-view Convolutional Neural Networks for

3D Shape Recognition. 2015 IEEE International

Conference on Computer Vision (ICCV), 945–953.

https://doi.org/10.1109/ICCV.2015.114

Wahl, E., Hillenbrand, U., & Hirzinger, G. (2003). Surflet-

pair-relation histograms: a statistical 3D-shape

representation for rapid classification. Fourth

International Conference on 3-D Digital Imaging and

Modeling, 2003. 3DIM 2003. Proceedings., 474–481.

https://doi.org/10.1109/IM.2003.1240284

Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M.,

& Solomon, J. M. (2019). Dynamic Graph CNN for

Learning on Point Clouds. ACM Transactions on

Graphics, 38(5), 1–12.

https://doi.org/10.1145/3326362

Wang, Y. Y., & Li, J. (2008). Featureselection ability of

the decisiontree algorithm and the impact of feature

selection/extraction on decisiontree results based on

hyperspectral data. International Journal of Remote

Sensing, 29(10), 2993–3010.

https://doi.org/10.1080/01431160701442070

Yandex. (2020a). CatBoost - Feature Importance.

Yandex. (2020b). CatBoost - open-source gradient

boosting library.

Yavartanoo, M., Kim, E. Y., & Lee, K. M. (2019). SPNet:

Deep 3D Object Classification and Retrieval Using

Stereographic Projection. Computer Vision – ACCV

2018. Lecture Notes in Computer Science, 11365, 691–

706. https://doi.org/10.1007/978-3-030-20873-8_44

Zhou, H.-Y., Liu, A.-A., Nie, W.-Z., & Nie, J. (2020).

Multi-View Saliency Guided Deep Neural Network for

3-D Object Retrieval and Classification. IEEE

Transactions on Multimedia

, 22(6), 1496–1506.

https://doi.org/10.1109/TMM.2019.2943740

Validating Results of 3D Finite Element Simulation for Mechanical Stress Evaluation using Machine Learning Techniques