
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera
Athanasios Tsoukalas
1
, Nikolaos Evangeliou
1
, Nikolaos Giakoumidis
2
and Anthony Tzes
1
1
Engineering Division, New York University Abu Dhabi, P.O. 129188, Abu Dhabi, U.A.E.
2
Core Technology Platform, New York University Abu Dhabi, P.O. 129188, Abu Dhabi, U.A.E.
Keywords:
Variable Object Tracking, Visual Homography, Optical Flow.
Abstract:
The visual detection and tracking of UAVs using a Pan-Tilt-Zoom (PTZ) camera attached to another aerial
platform is the scope of this article. The long-term tracker is performing image background subtraction using
visual homography and is used to initialize a short term tracker that works in parallel to enhance the tracking for
various motions. The moving UAV is detected using optical flow concepts and its bounding box encapsulates
its detected features. A Kalman predictor provides a robust smooth tracking of the bounding box in the
temporary absence of a detected UAV. The camera pans and tilts so as the tracked UAV is centered within
its Field-of-View and zooms in order to expand the UAV’s view. Experimental results are offered using an
evader-tracker UAV-group to validate the presented tracking algorithm.
1 INTRODUCTION
In this work the subject of the Long Term Tracking
(LTT) of a target UAV from another one equipped
with a Pan - Tilt - Zoom (PTZ) camera is consid-
ered. The estimation of the strong background im-
age feature points in comparison to those of a mov-
ing object is performed through a comparison of the
image optical flows and the predicted position of the
feature points according to the Homography transfor-
mation derived between feature points found in pre-
vious frame and the estimate in the current frame.
A Kalman prediction filter (Paul and Musoff, 2015)
can smooth the trajectory in the presence of noisy
measurements, while a correlation based tracking al-
gorithm is also used in combination with our LTT
scheme to account for the cases where the UAV
blends with the background.
Previous research on Variable Object Tracking
(VOT) has focused on strong image features matching
and Homography. In (Eshel and Moses, 2008) mul-
tiple static cameras are used to infer multiple mov-
ing targets, using the homography of three planes
parallel to the floor between each pair of cameras.
In (Arr
´
ospide et al., 2010) the ground plane is de-
tected using a single moving camera, by finding the
homography between the ground planes in successive
images, using a feature matching approach. These
methods assume that the floor or a top down view
is always present in the camera view. In (Cui et al.,
2019) a moving object segmentation is performed
from stationary or moving cameras based on homog-
raphy constraints across multiple frames, that de-
scribes the background motion, without assuming a
planar scene using a pixel precision. In (Dey et al.,
2012) the detection of independently moving fore-
ground objects in non-planar scenes captured by a
moving camera is performed, using a multi frame
monocular epipolar constraint of camera motion. The
method applies optical flow across the whole image
between consecutive frames, that scales exponentially
in performance loss as the image resolution is higher.
In (Viswanath et al., 2015) foreground object seg-
mentation is performed with a background modelling
technique that models each pixel with a single Spatio-
Temporal Gaussian. In (Sheikh et al., 2009) objects
are tracked using a freely moving camera with no
assumptions that the background approximated by a
plane, by building a sparse background model by es-
timating a compact trajectory basis from trajectories
of salient features across the video. Following the
background subtraction by removing trajectories that
lie within the space spanned by the basis, builds the
foreground and background appearance models. Then
an optimal pixel-wise foreground/background label-
ing is obtained by efficiently maximizing a posterior
function. In (Fu et al., 2016) the algorithm tracks
by finding feature correspondences in a way that an
improved binary descriptor is developed for global
feature matching, while an iterative Lucas–Kanade
90
Tsoukalas, A., Evangeliou, N., Giakoumidis, N. and Tzes, A.
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera.
DOI: 10.5220/0010112900900097
In Proceedings of the International Conference on Robotics, Computer Vision and Intelligent Systems (ROBOVIS 2020), pages 90-97
ISBN: 978-989-758-479-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

optical flow algorithm is employed for local feature
tracking and a local geometric filter (LGF) module
maintaining pairwise geometric consistency is used to
identify outliers.
In all of the above methods (excluding (Viswanath
et al., 2015)), the feature points are identified and
matched between frames, resulting in one extra step
dependent on both the feature matching between
frames algorithm and the feature selection algorithm.
In our method we do not perform any feature match-
ing, using directly the positions estimated by the op-
tical flow as next-frame features and calculate the
homography matrix based on the features found in
the previous frame and the estimated by the optical
flow in the current frame. This allows for a one-
to-one correspondence of features positions between
frames, removing any ambiguity as to which fea-
tures are matched and dramatically enhances perfor-
mance as there is no need for a feature matching step.
In (Viswanath et al., 2015), similar to our method the
feature points in the previous frame are tracked using
an optical flow method and a Homography is calcu-
lated for the background pixels, under the assump-
tion of an initial background state image and subse-
quently updating a distribution of background proba-
bility of each pixels in the new frame. This is used to
model the new background and perform background
subtraction using the entire new background image
as mask, requiring a significant computational bur-
den.This method does not behave well in the absence
of many background points to estimate the Homogra-
phy, and the foreground object estimation needs more
computations, since it operates on the whole image
for both the background transformation/subtraction.
In Section 2 the visual tracking problem of the
UAV from another airborne UAV statement is pro-
vided, followed by the case of identifying a flying
object using the Homography based method in Sec-
tion 2.1. In Section 3 the method of estimating the im-
age based optical flow is discussed using the current
and previous image frames. In Section 4 the method
of estimating the image flow for background image
features based on the Homography transformation de-
rived between image feature points found in previous
and current frames is discussed as well as the method
of comparing the two flows in order to evaluate which
parts of the image are background, that is when the
optical flow velocity vectors match closely those of
the expected by the Homography based flow estima-
tion of the image features corresponding to the back-
ground. The method of calculation of the bounding
box around the tracked target UAV points that have
been identified as foreground is also discussed. In
Section 5 the implementation of the Kalman predic-
tor for the smooth follow of the tracked UAV dur-
ing tracking window estimation noise is discussed. In
Section 6 a correlation based tracker is considered and
described, for further enhancing the ability to track
the object when the flow based method is not pro-
viding a result due to object blending with the back-
ground. In Section 7 the control of the PTZ camera
motion to track the target UAV is discussed along with
the overall algorithm. In Section 8 the results of an
experiment of tracking a UAV from a flying UAV pur-
suer is presented and analyzed.
2 AIRBORNE
VISUAL-TRACKING OF UAV
The algorithms are running locally on a mini i7-based
Intel NUC PC on board of an enhanced Vulkan UAV
shown in Figure 1.
Figure 1: Tracker UAV with mounted PTZ-camera.
Real time LTT of an object using a video-stream is
a complex task due to the limited information we have
about the object. The various correlation methods
give a good tracking performance, given the motion
is not very fast and can keep the correlation strong
between frames, but fail when the motion is fast and
loose the tracking window. These must be initial-
ized with a starting window that engulfs the object
to track. Thus a LTT-scheme based on object motion
is required in order to track a general object across
all motions regions, occlusion and change of appear-
ance. Such a scheme is proposed in this article, en-
hanced with a correlation based tracker for the cases
where the object blends with the background since its
motion which can be slow or not moving relative to it.
2.1 Object Tracking Method using
Homography
The background subtraction method used in order
to identify the moving object motion is relying
only on visual feedback and homography calcula-
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera
91
tions (Szeliski, 2010) between two frames. This
method is robust against general disturbances and per-
forms well when IMU measurements are not avail-
able. Initially a strong image features set is identi-
fied on the previous camera frame and an optical flow
technique is used to estimate the position of the fea-
tures in the current frame, as shown in Figure 2. The
method involves the discovery of special image areas
with specific characteristics. The feature set is a col-
lection of pixel points in the camera image, while var-
ious algorithms are available for the discovery of im-
age features (Tareen and Saleem, 2018).
0: Initialize
1: Get current image I
I
I
2: Detect corner features
in I
3: Calculate optical
flow from toI I
4: Calculate Homography
using features computed in
steps 2 and 3
5: Identify foreground
features
i-1
i-1
i-1
i-1
i-1
i-1
6: Dilation of moving points
7: Bounding box calculation
8: Bounding box prediction using Kalman filter
9: PTZ-camera PID control for VOT
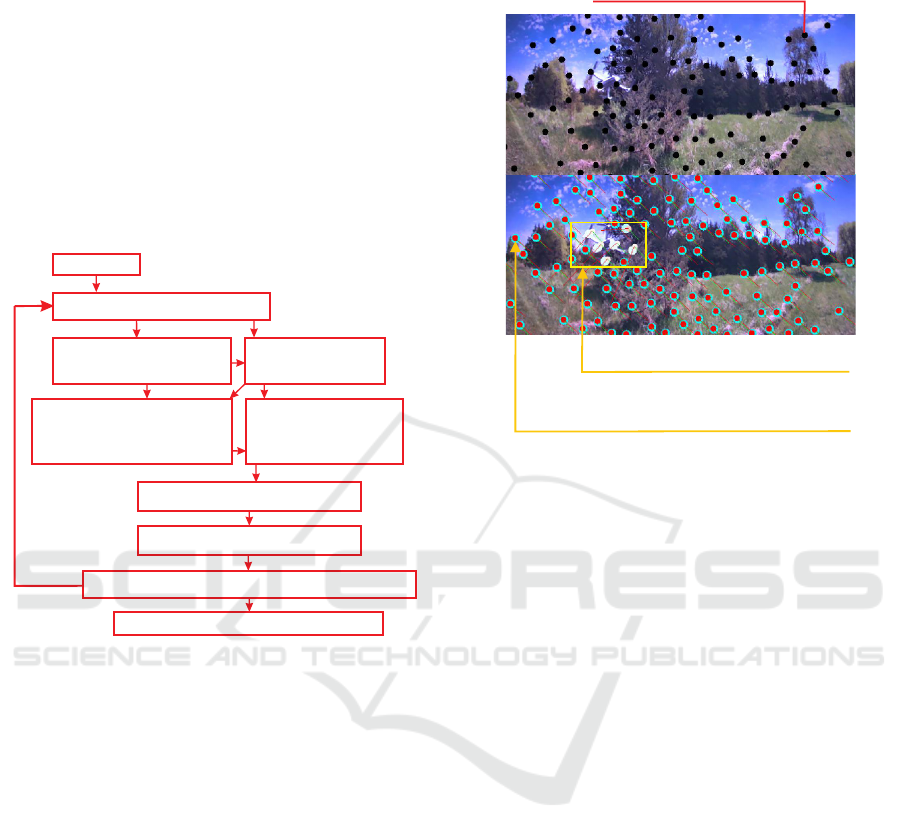
Figure 2: Visual Homography based tracking.
OpenCV’s “goodFeaturestoTrack” (Shi and
Tomasi, 1994) algorithm was used for finding the
strong corners image features in our experiments
Under the assumption that the background holds the
majority of the pixels with a consistency in displace-
ment, a homography is calculated that transforms the
features positions from the previous to the current
frame, which correspond to the background pixels.
The previous frame features are then transformed
using the homography to get their position in the
current frame. We assume that the background points
transformed with the homography that corresponds
mainly to the background pixels group will coincide
with the estimated ones by the optical flow, while
the moving objects features estimated by the optical
flow will diverge from the homography transformed
pixels, as shown in Figure 3.
The pixels that correspond to static background
objects will follow the predicted motion by the Ho-
mography transformation and coincide to the po-
sitions predicted by an optical flow based estima-
tion, while the rest will be classified as belonging to
Estimated UAV bounding box
after background points removal
Optical flow and Homography based estimated
positions of features in the current frame
in red and cyan respectively.
Feature points positions
in previous image frame
Brightness of circles is proportional to divergence
of the two estimates of features position.
(When 0 assume features are on background)
d
d
≈
Figure 3: Homography/Optical flow tracking method.
moving objects of interest (Figure 4). The calcula-
tions of the optical flow follow the Lucas - Kanade
method (Lucas and Kanade, 1981) with an extension
using a pyramidal scheme with variable image resolu-
tions (Bouguet, 2000). The basic optical flow premise
is to discover the position of an image feature from
previous frame, in the current frame.
One downside of the technique is that when the
tracked object remains static and blends with the
background, it cannot be identified, thus a correlation
short term tracker relying on the MOSSE tracking al-
gorithm (Bolme et al., 2010) is used. This identifies
the UAV’s position until new estimated positions from
the flow based method are available. The benefit of
the LTT-schemer is that requires zero a priori infor-
mation, unlike the methods that require prior knowl-
edge of the target bounding window for initialization.
2.2 Homography Calculation
The homography or perspective transform can be for-
mulated as a 3 × 3 operator H on homogeneous coor-
dinates
x
0
i
y
0
i
1
= H ˜x =
h
00
h
01
h
02
h
10
h
11
h
12
h
20
h
21
h
22
x
i
y
i
1
. (1)
The resulting homogeneous coordinates x
0
i
, y
0
i
are nor-
malized as
ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems
92

t
p
t
p
t-1
t-1
t-1
p
p
p
Target drone
Static Background
Image features in frame t-1
Camera motion
Camera motion
Estimated features in frame using optical flow based
on the drone position
t
Estimated features in frame using Homography
transformation
t
Estimated background - foreground features in frame t
t
p
t
p
d > threshold
d ≈ 0
d ≈ 0
Background
Foreground
flow
flow
hmg
hmg
Figure 4: Foreground identification method.
x
0
i
=
h
00
x
i
+ h
01
y
i
+ h
02
h
20
x
i
+ h
21
y
i
+ h
22
, y
0
i
=
h
10
x
i
+ h
11
y
i
+ h
12
h
20
x
i
+ h
21
y
i
+ h
22
, (2)
while the operator H is calculated such that minimizes
the back projection error
∑
i
x
0
i
−
h
00
x
i
+ h
01
y
i
+ h
02
h
20
x
i
+ h
21
y
i
+ h
22
2
+
y
0
i
−
h
10
x
i
+ h
11
y
i
+ h
12
h
20
x
i
+ h
21
y
i
+ h
22
2
. (3)
In order to get a good estimation of the transfor-
mation matrix in the presence of outliers, which may
include foreground points that move not inline with
the background point majority, the RANSAC method
is used to estimate the homography matrix using this
subset followed by a simple least-squares algorithm to
compute the quality of the computed homography (de-
fined by the number of inliers). The best subset is then
used to produce the initial estimate of the homography
matrix. The computed homography matrix is refined
further with the non linear Levenberg-Marquardt opti-
mization (Levenberg, 1944; Marquardt, 1963) method
to further reduce the re-projection error.
3 OPTICAL FLOW ON SPARSE
IMAGE FEATURES
When the tracker UAV is moving, static camera based
background subtraction algorithms cannot provide an
accurate UAV-tracking, and another background sub-
traction method needs to be implemented for this case.
The method involves the discovery of special image ar-
eas with specific characteristics in the camera image,
which we note as the image feature set F
s
t
at time t. The
feature set is a collection of pixel points in the camera
image p
t
= [px
t
, py
t
]. Various algorithms are available
for the discovery of image features (Tareen and Saleem,
2018).
OpenCV’s “goodFeaturestoTrack” (Shi and Tomasi,
1994) adapted to run on the GPU using the “se-
tUseOpenCL” of the OpenCL module and UMat image
holder is employed to find the strong corners image fea-
tures. This algorithm calculates the corner quality mea-
sure at every source image pixel using the Minimum
Eigenvalue or the Harris method. For each of the dis-
covered image features of the previous image frame, the
optical flow F
v
t
is derived as a collection of velocity vec-
tors that correspond to each of the image features. For
the optical flow estimation of the discovered image fea-
tures, the OpenCV function “calcOpticalFlowPyrLK” is
used. The method operates on a sparse feature set using
the iterative Lucas-Kanade method with pyramids and
the inputs are the current and previous frames as well as
the image features identified from the previous frame.
The output is the estimated feature position in the cur-
rent frame. An example of the feature matching between
the current and previous frames is presented in Figure 5.
Figure 5: Image feature matching between successive
frames.
The algorithm also provides a status flag for each
point that describes whether a flow was found for the
specific point. The calculations of the optical flow fol-
low the Lucas - Kanade method (Lucas and Kanade,
1981) with the an extension using a pyramidal scheme
with variable image resolutions (Bouguet, 2000). The
basic optical flow premise is to discover the positioning
of an image feature in the previous frame, in the current
captured frame.
OpenCV’s calcOpticalFlowPyrLK function is used
accepting as inputs the previous camera image, and the
feature points selected in the previous image to estimate
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera
93

the optical flow on the current camera image. The output
is the estimated points along with status number for each
estimation, which has a value of one if an estimation of
the point in the new image is found, otherwise is zero.
4 HOMOGRAPHY-BASED
TRACKING
The tracking method differentiates the foreground to the
background image features discovered in the previous
image frame. The estimated background points given by
the transformation of those points using a Homography
matrix are compared to the foreground ones and their
estimated positions by an optical flow method, in the
current frame.
Given an image g
t−1
in time t − 1, we derive the es-
timation of the positions of the selected image feature
points set F
s
t
in the image g
t
in time t, based on the Ho-
mography calculated between the strong feature points
of the previous and current camera frames, as described
in the previous sections. Then an optical flow method
as described in Section 3 is used for the same estimation
of the feature point positions. The two resulting posi-
tions are compared to distinguish the background points
from the moving ones, considering the estimation points
with distance less than a threshold would belong to the
background. The optical flow provides the estimation
ˆp
f low
t
of the position of a feature point in the previous
frame g
t−1
, in the current frame g
t
for the p
t
point in
the previous frame and an estimation of the point ˆp
Hmg
t
is also provided from the Homography based transfor-
mation on the feature points set of the previous frame
g
t−1
. The distance b
t
= || ˆp
f low
t
− ˆp
Hmg
t
|| is evaluated
and if b
t
(p
t
) ≥ b
bkgd
, ∀p
t
∈ F
s
t
(image feature point set),
then the point p
t
is considered as moving, otherwise as
a background one.
The foreground points correspond to those describ-
ing the UAV; a dilation operator followed by the compu-
tation of a predicted bounding around the blob of points
that surrounds the UAV, as shown in Figure 6 bottom
left window, using OpenCV’s function “Find Contours”
in combination with the “approxPolyDP” function that
approximates found contours with polylines that are in-
serted into the “boundingRect” function to create the
bounding box around the polyline. The aforementioned
search is performed at each frame and the performance
of the system using a 960 × 540 pixels is at 65fps on
the airborne i7 CPU Intel NUC PC. The NUC’s GPU
is used with OpenCL library for OpenCV to enhance
the performance of the optical flow and image manip-
ulation calculations. When the background has static
objects across a wide range of distances to the tracker
UAV, some points may be identified as foreground, thus
a second background layer is assumed and the Homog-
raphy is recalculated using this new subset, in order to
identify the remaining background points. It should be
noted that this layer can be computed extremely fast due
to the lack of need to compute the optical flow.
Estimated UAV bounding box
after background points removal
and dilation of the foreground
points
Estimated image feature points
corresponding to the UAV
Strong image feature points
Figure 6: Estimated image features on tracked UAV.
5 KALMAN FILTER TRACKING
OF BOUNDING BOX
A Kalman filter prediction scheme tracks the motion
smoothly in the absence of a tracking window (or short
time sensor malfunction) in some frames and provides
the an estimate of the UAV’s trajectory. The Kalman
predictor uses a state vector X = [x, y, ˙x, ˙y, ¨x, ¨y, w, h]
comprising of the position (Velocity) of the center of
the tracking window [x, y] ([ ˙x, ˙y), and the width and
height of the window w, h. The estimated vector m
e
=
[x
m
, y
m
, ˙x
m
, ˙y
m
, w
m
, h
m
] contains the currently identified
window center x
m
, y
m
, its velocity ˙x
m
, ˙y
m
and box’s
width and height w
m
, h
m
. The ˆx
k
-estimate of X is found
in a recursive manner as
ˆx
k
= F
k
ˆx
k−1
ˆ
P
k
= F
k
ˆ
P
k−1
F
T
k
+ Q
k
Under the assumption of a constant acceleration, the
state transition matrix is
F
k
=
I
2
dtI
2
dt
2
2
I
2
O
2
O
2
I
2
dtI
2
O
2
O
2
O
2
I
2
O
2
O
2
O
2
O
2
I
2
where dt is the time delta between two consec-
utive frames, and I
2
(O
2
) is the 2 × 2 identity
(zero) matrix . The expected process noise covari-
ance matrix of the model is assumed to be Q =
diag(σ
x
, σ
y
, σ
˙x
, σ
˙y
, 0, 0, σ
w
, σ
h
). The conversion of the
state space to measurement units is performed through
the measurement adaptation matrices m
e
= H
k
ˆx
k
, and
ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems
94

S
e
= H
k
P
k
H
T
k
, where
H
k
=
I
2
O
2
O
2
O
2
O
2
I
2
O
2
O
2
O
2
O
2
O
2
I
2
.
For our tracking window measurements, we define
R
k
= diag(σ
x
m
, σ
y
m
, σ
˙x
m
, σ
˙y
m
, σ
w
m
, σ
h
m
) as the covari-
ance of the estimated window parameters measurement
noise induced uncertainty and z
k
the mean of the mea-
surements. The final measurement update ˆx
k
t
and the
covariance
ˆ
P
k
t
are defined as
ˆx
k
t
= ˆx
k
t−1
+ K(z
k
− H
k
ˆx
k
) (4)
ˆ
P
k
t
= P
k
t−1
− KH
k
P
k
t−1
(5)
where the Kalman gain K is given by
K = P
k
H
T
k
(H
k
P
k
H
T
k
+ R
k
)
−1
(6)
The measurement matrix is updated with the esti-
mated bounding box position-width-height and velocity
calculated using the position estimations in previous and
current frames and the time between them.
6 CORRELATION BASED MOSSE
TRACKING ALGORITHM
In the case where a UAV is hovering, the optical flow
method may not provide results as essentially the UAV
can be considered as background. To avoid this behav-
ior we use the MOSSE tracking algorithm (Bolme et al.,
2010) around the tracking window to check if the cor-
relation to the previous frame stays strong, and decide
whether to keep the window to the same position or
move it to some other position, according to the latest
measurements. The MOSSE algorithm requires an ini-
tial bounding box around the target, which we provide
through our LTT when the confidence is high enough
across multiple frames and the MOSSE tracking win-
dow to our estimated tracking window have distance be-
yond a threshold. A weight is given based on how strong
the correlation and how far the new measurement from
the previous to make the final decision. When MOSSE
algorithm alone is used to track the target UAV, the re-
sults are generally adequate, but the algorithm needs an
initial tracked object bounding box and also can fail to
provide information for the loss of tracking, getting lo-
cally trapped in an image position different than the re-
quired one. Thus an LTT-scheme is needed for MOSSE
re-initialization in loss of tracking. The MOSSE algo-
rithm uses the correlation of a filter calculated by the
previous bounding box engulfed image and the current
image, to track closeness of the current frame to the ini-
tial target provided by the LTT. The calculations are per-
formed using FFT, due to the fact that correlation can be
expressed as the element wise multiplication of the in-
dividual FFT on the correlation filter and current image.
Thus the correlation between the input image F = F(f )
and the filter H = F(h) is expressed as
G = F H
∗
. (7)
The filter is initially trained by the UAV image,
provided by the optical flow based method that deter-
mines the initial tracked object bounding box. The tar-
get is then tracked by correlating the current filter over a
search window in the next frame and the maximum cor-
relation output position indicates the new position of the
target. The filter is then retrained based on the newly
identified position. The filter is defined such that it min-
imizes the square error sum between the actual and de-
sired output of the convolution.
min
H
∗
∑
i
|F
i
H
∗
− G
i
|
2
. (8)
resulting in
H
∗
=
∑
i
G
i
F
∗
i
F
i
F
∗
i
. (9)
The numerator can be interpreted as the correlation
between the input and the desired output and the de-
nominator is the input energy spectrum. The training
set is constructed using random affine transformations
to generate eight small perturbations ( f
i
) of the track-
ing window in the initial frame. Training outputs (g
i
)
are also generated with their peaks corresponding to the
target center. During tracking, a UAV-target can often
change appearance by changing its rotation, scale, pose,
by moving through different lighting conditions. There-
fore, filters need to quickly adapt in order to follow ob-
jects. Running average is used for this purpose. The it-
erative MOSSE filter after the initialization is computed
as
H
∗
i
=
A
i
B
i
=
nG
i
F
∗
i
+ (1 − n)A
i−1
nF
i
F
∗
i
+ (1 − n)B
i−1
(10)
where n is the learning rate. MOSSE’s performance
ws found to be suitable for real time tracking. In Fig-
ure 6, the MOSSE tracking window is shown in blue box
around the tracked UAV. The Kalman tracking window
is represented by the red box and the magenta one cor-
responds to the predicted tracking object bounding box
by the optical flow and Homography method.
7 PTZ CAMERA CONTROL
The PTZ camera moves according to commands issued
by its programming API. A PID controller has been de-
vised to track the discovered target UAV by turning the
camera towards the UAV with the goal to center it on the
screen at every frame. When the target has been near
centered, a zoom action is performed in order to extend
the target’s bounding box thus eliminating a portion of
the background that may affect the tracking result. The
overall algorithm for tracking a target UAV is presented
in the sequel.
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera
95
1: Initialize algorithm and retrieve first frame I
0
.
2: Retrieve current image I
i
and buffer I
i−1
.
3: Detect the coordinates (x, y) of image feature set
g
i−1
, in previous frame I
i−1
.
4: Calculate the optical flow from I
i−1
to I
i
such that
g
i−1
corresponds to the g
i
features.
5: Estimate background pixels position ˆg
i
for every
g
i−1
feature using Homography transformation.
6: Subtract ˆg
i
from the optical flow g
i
to get estima-
tion distance b
t
= || ˆp
f low
t+1
− ˆp
Hmg
t+1
||.
7: The feature points p
t
in g
i
where b
t
(p
t
) ≥
b
bkgd
∀p
t
∈ g
t
are considered moving, otherwise these
are marked as background.
8: Dilate the foreground points and extract the
polygonal boundaries around point concentrations.
9: Generate bounding boxes around identified fea-
tures clusters and select the largest one that corresponds
to the tracked object.
10: Initialize and run in parallel the MOSSE corre-
lation based tracker when the measurements confidence
is high across multiple frames.
11: Use a Kalman filter to smoothly track the
MOSSE estimated tracking window in each frame.
12: Use the PID controller to direct the PTZ to the
tracked object.
13: Repeat step 2.
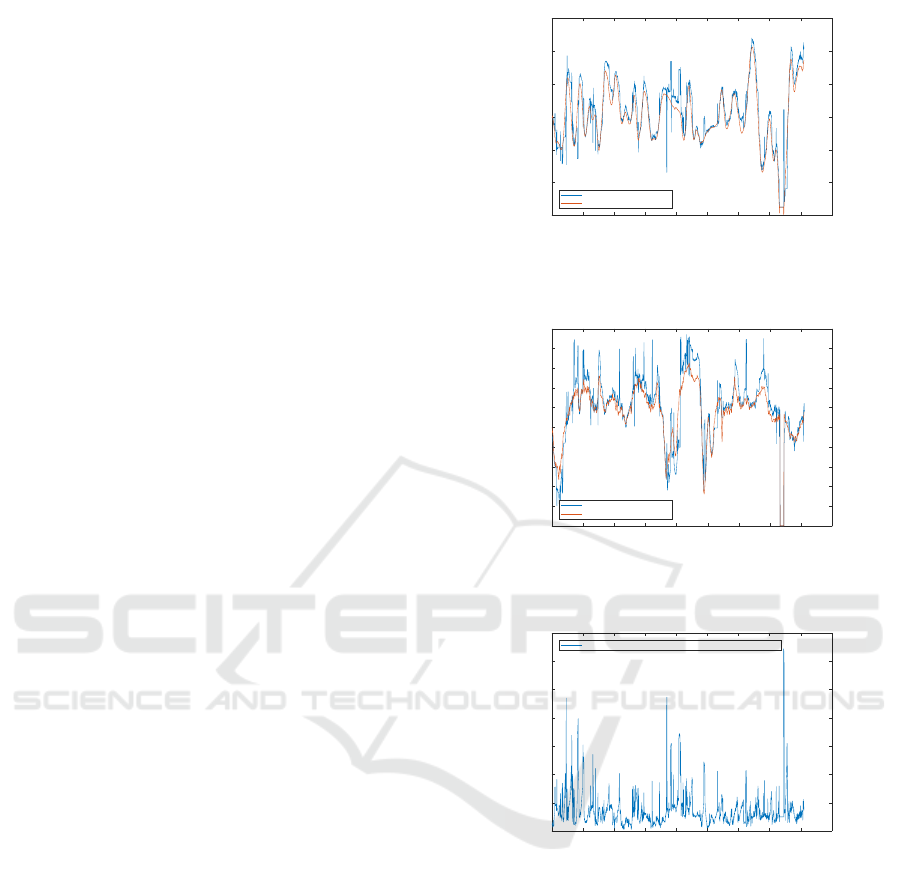
8 EXPERIMENTAL STUDIES
The results of an airborne tracking of a UAV is presented
in this section. Both UAVs are monitored by a Motion
Capture System (MoCaS) using a set of 24 Vicon cam-
eras. Figures 7 to 9 show the tracking results in pix-
els. It is shown that the tracking using the Homogra-
phy based method closely follows the tracked UAV and
is further enhanced when the MOSSE correlation based
tracking is also used to account for the cases where there
is no position estimate. The MOSSE algorithm is re-
initialized based on the measurements by our method,
given a confidence of three consecutive frames with an
estimated object position that does not diverge beyond
a threshold. In the case where no measurement track-
ing window or MOSSE tracking window is estimated,
the previous known estimation is used respectively. A
presentation of the algorithm working on smooth mo-
tion videos and multiple targets can be previewed in the
videos in (Tsoukalas, 2020).
9 CONCLUSIONS
A method to determine the trajectory of a moving UAV
has been presented in this work, using a PTZ camera.
The foreground is discriminated from the background
based on the comparison of the predicted background
0 200 400 600 800 1000 1200 1400 1600 1800
Video Frame
0
200
400
600
800
1000
1200
Tracked object average position - X axis
Tracked object X axis average position from Measurement and MOSSE tracked estimations
MOSSE-Measurement Average
Vicon
Figure 7: Estimation of X axis of the tracked UAV using
MOSSE and Measurements estimations.
0 200 400 600 800 1000 1200 1400 1600 1800
Video Frame
50
100
150
200
250
300
350
400
450
500
550
Tracked object average position - Y axis
Tracked object Y axis average position from Measurement and MOSSE tracked estimations
MOSSE-Measurement Average
Vicon
Figure 8: Estimation of Y axis of the tracked UAV using
MOSSE and Measurements estimations.
0 200 400 600 800 1000 1200 1400 1600 1800
Video Frame
0
100
200
300
400
500
600
700
Tracked object distance to Vicon measured real position
Distance of averaged estimated tracked object position to Vicon measurement
MOSSE and Measurement average position to Vicon positions distance
Figure 9: Distance betwen Tracked UAV estimated position
and MoCaS real position.
image features motion using the Homography derived
by image feature sets between two successive frames
and the motion estimated by the optical flow between
these frames. The optical flow long term tracking and a
correlation short term tracking are combined to provide
a robust tracking scheme. A Kalman predictor is also
used in order to smoothly follow the trajectory and in-
crease the tolerance of the system to the tracked UAV’s
bounding box prediction temporal errors.
ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems
96

REFERENCES
Arr
´
ospide, J., Salgado, L., Nieto, M., and Mohedano, R.
(2010). Homography-based ground plane detection
using a single on-board camera. Intelligent Transport
Systems, IET, 4:149 – 160.
Bolme, D., Beveridge, J., Draper, B., and Lui, Y. (2010). Vi-
sual object tracking using adaptive correlation filters.
In Proceedings of the IEEE Computer Society Con-
ference on Computer Vision and Pattern Recognition,
pages 2544–2550.
Bouguet, J. Y. (2000). Pyramidal implementation of the
lucas kanade feature tracker. Intel Corporation, Mi-
croprocessor Research Labs.
Cui, Z., Jiang, K., and Wang, T. (2019). Unsupervised
moving object segmentation from stationary or mov-
ing camera based on multi-frame homography con-
straints. Sensors, 19:4344.
Dey, S., Reilly, V., Saleemi, I., and Shah, M. (2012). De-
tection of independently moving objects in nonplanar
scenes via multi-frame monocular epipolar constraint.
In Computer Vision – ECCV 2012, pages 860 – 873.
Eshel, R. and Moses, Y. (2008). Homography based multi-
ple camera detection and tracking of people in a dense
crowd. In 2008 IEEE Conference on Computer Vision
and Pattern Recognition.
Fu, C., Duan, R., Kircali, D., and Kayacan, E. (2016). On-
board robust visual tracking for UAVs using a reliable
global-local object model. Sensors, 16:1406.
Levenberg, K. (1944). A method for the solution of cer-
tain non-linear problems in least squares. Quarterly
of Applied Math., 2(2):164–168.
Lucas, B. and Kanade, T. (1981). An iterative image regis-
tration technique with an application to stereo vision.
In Proceedings of the 7th International Joint Confer-
ence on Artificial Intelligence, volume 2, pages 674–
679.
Marquardt, D. (1963). An algorithm for least-squares es-
timation of nonlinear parameters. SIAM Journal on
Applied Mathematics, 11(2):431–441.
Paul, Z. and Musoff, H. (2015). Fundamentals of Kalman
Filtering: A Practical Approach. American Institute
of Aeronautics and Astronautics.
Sheikh, Y., Javed, O., and Kanade, T. (2009). Background
subtraction for freely moving cameras. Proceedings of
the IEEE International Conference on Computer Vi-
sion, pages 1219–1225.
Shi, J. and Tomasi, C. (1994). Good features to track. In
Proceedings of IEEE Conference on Computer Vision
and Pattern Recognition, pages 593–600.
Szeliski, R. (2010). Computer Vision: Algorithms and Ap-
plications. Springer-Verlag, Berlin, Heidelberg, 1st
edition.
Tareen, S. A. K. and Saleem, Z. (2018). A comparative anal-
ysis of sift, surf, kaze, akaze, orb, and brisk. In 2018
International Conference on Computing, Mathemat-
ics and Engineering Technologies (iCoMET), pages
1–10.
Tsoukalas, A. (2020). Tracking videos using Homography
based algorithm. https://drive.google.com/open?id=
1MgL1RoW7r36ftm aloNzV GJstS4L7Wr.
Viswanath, A., Behera, R., Senthamilarasu, V., and Kutty,
K. (2015). Background modelling from a moving
camera. Procedia Computer Science, 58:289–296.
Airborne Visual Tracking of UAVs with a Pan-Tilt-Zoom Camera
97
