
Detecting Unsatisfiable Pattern Queries under Shape Expression Schema
Shiori Matsuoka
1
and Nobutaka Suzuki
2
1
Graduate School of Library, Information and Media Studies, University of Tsukuba, 1-2, Kasuga, Tsukuba, Ibaraki, Japan
2
Faculty of Library, Information and Media Science, University of Tsukuba, 1-2, Kasuga, Tsukuba, Ibaraki, Japan
Keywords:
Shape Expression, Pattern Query, Satisfiability.
Abstract:
Among queries for RDF/graph data, pattern query is the most popular and important one. A pattern query
that returns empty answer for every valid graph is clearly useless, and such a query is called unsatisfiable.
Formally, we say that a pattern query q is unsatisfiable under a schema S if there is no valid graph g of S
such that the result of q over g is nonempty. It is desirable that unsatisfiable pattern queries can be detected
efficiently before being executed since unsatisfiable query may require much execution time but always reports
empty answer. In this paper, we focus on Shape Expression (ShEx) as schema, and we propose an algorithm
for detecting unsatisfiable pattern queries under a given ShEx schema. Experimental results suggest that our
algorithm can determine the satisfiability of pattern query efficiently.
1 INTRODUCTION
Over many years, RDF/graph has been a popular
data model and used for various kinds of applica-
tions, Linked Open Data, social networks, citation
graph, and so on. For such data, RDF Schema
(RDFS) is sometimes used as a schema definition
language. However, RDFS is an ontology language
rather than a schema language and is not necessarily
suitable for describing structures of graph data (Sta-
worko et al., 2015). Due to this, a new schema lan-
guage called Shape Expression (ShEx) has been con-
sidered under W3C Draft Community Group (Baker
and Prud’hommeaux, 2019). ShEx is designed for
capturing structural features of RDF data rather than
its ontological semantics, and already used in a vari-
ety of areas (Thornton et al., 2019).
Among queries for RDF/graph data, pattern query
is the most popular and important one. A pattern
query that returns empty answer for every valid graph
is clearly useless, and such a query is called unsat-
isfiable. Formally, for a pattern query q and a ShEx
schema S, we say that q is unsatisfiable under S if
there is no valid graph G of S such that the answer of
q for G is not empty. As a simple example, consider
the ShEx schema in Fig. 1 having the definitions of
four types t
1
,t
2
,t
3
,t
4
. Then Fig. 2 illustrates an exam-
ple of pattern query over the schema. Since v
1
cannot
have “tel” and “email” at the same time due to the def-
inition of t
2
, the pattern query is unsatisfiable. Here,
suppose that a user writes an unsatisfiable query q and
that he/she executes q over a graph data G. Then q tra-
verses nodes/edges of G but fails to find any answer.
Since the size of recent RDF/graph data tend to be
very large, executing such a query may requires huge
computation cost. Therefore, it is desirable that un-
satisfiable queries can be detected efficiently before
being executed.
In this paper, we propose an algorithm for detect-
ing unsatisfiable pattern queries under ShEx schema.
For a pattern query q and a ShEx schema S, the algo-
rithm decomposes S into connections between types
of S, then checks the matchability between the type
connections and edges of q. If every edge of q is
“safely” matched by a connection in S, then the al-
gorithm answers that “q is satisfiable,” otherwise “q
is unsatisfiable.” Although this problem is intractable
in general, our preliminary experiments suggest that
our algorithms can detect unsatisfiable pattern queries
efficiently.
Recently, an architectural schema for business
document processing is proposed (Cristani et al.,
2018). Business documents are large amounts of date
and may be processed using ShEx. For example,
some efforts have been spent upon such documents,
in which unifying semantics by ShEx could be fruit-
fully used. Our problem is worth considering in that
field.
Matsuoka, S. and Suzuki, N.
Detecting Unsatisfiable Pattern Queries under Shape Expression Schema.
DOI: 10.5220/0010171602850291
In Proceedings of the 16th International Conference on Web Information Systems and Technologies (WEBIST 2020), pages 285-291
ISBN: 978-989-758-478-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
285

< t
1
>{
student@ < t
2
>
∗
}
< t
2
>{
supervisor@ < t
3
>
?
||
takes@ < t
4
>
+
||
(tel xsd : string | email xsd : string)
}
< t
3
>{
teaches@ < t
4
>
+
}
< t
4
> {
}
Figure 1: Example of ShEx schema.
Figure 2: Example of unsatisfiable pattern query.
1.1 Related Work
Satisfiablity of query has been a major problem of
database and document management field. A num-
ber of studies on XPath satisfiability problem un-
der DTDs or XML Schema have been made, e.g.,
(Groppe and Groppe, 2007; Montazerian et al., 2007;
Benedikt et al., 2008; Ishihara et al., 2013; Figueira,
2018). Geneves et al. proposes a comprehensive tool
for checking satisfiability of XPath expressions un-
der schema (Geneves et al., 2011). However, XML is
based on ordered tree data model and XPath query can
also be represented by tree, and thus their query/data
models are quite different from that of this paper.
Zhang et al. consider satisfiability of pattern query
without schema (Zhang et al., 2016). To the best of
the authors’ knowledge, however, no studies on satis-
fiability of pattern queries under ShEx schemas have
been made so far.
2 PRELIMINARIES
Let Σ be a set of labels. A labeled directed graph
(graph for short) is denoted G = (V, E), where V is a
set of nodes and and E ⊆ V × Σ ×V is a set of edges.
Let e ∈ E be an edge labeled by l ∈ Σ from a node
v ∈ V to a node v
0
∈ V . Then e is denoted (v, l, v
0
),
v is called source, and v
0
is called target. A pattern
query (query for short) is also represented as a graph
q = (V (q), E(q)). For example, Fig. 3 illustrates a
graph G and Fig. 4 illstrates a query q and its answer
over G.
Figure 3: Example of valid graph G.
In XML data model, sibling nodes are ordered. On
the other hand, in RDF/graph data model the order
among sibling nodes are less significant and thus sib-
ling nodes are treated as unordered. Thus ShEx uses
regular bag expression (RBE) to represent the node
type (Staworko et al., 2015). RBE is defined simi-
lar to regular expressions except that RBE uses un-
ordered concatenation instead of ordered concatena-
tion. Let Γ be a set of types. Then RBE over Σ × Γ is
recursively defined as follows.
• ε and a :: t ∈ Σ × Γ are RBEs.
• If r
1
, r
2
, ·· · , r
k
are RBEs, then r
1
|r
2
|· ·· |r
k
is an
RBE, where | denotes disjunction.
• If r
1
, r
2
, · · · , r
k
are RBEs, then r
1
k r
2
k · · · k r
k
is
an RBE, where k denotes unordered concatena-
tion.
• If r is an RBE, then r
[n,m]
is an RBE, where n ≤ m.
[n, m] is called interval. In particular, r
?
= r
[0,1]
,
r
∗
= r
[0,∞]
, and r
+
= r
[1,∞]
.
For example, let r = (a :: t
1
|b :: t
2
) k c :: t
3
be an RBE.
Since k is unordered, r matches not only a :: t
1
c :: t
3
and b :: t
2
c :: t
3
but also c :: t
3
a :: t
1
and c :: t
3
b :: t
2
.
A ShEx schema is denoted S = (Σ, Γ, δ), where Γ
is a set of types, δ is a function from Γ to the set of
RBEs over Σ × Γ. For example, the schema in Fig. 1
can be denoted S = (Σ, Γ, δ), where
Σ = {teaches, student, supervisor, takes, tel,
email},
Γ = {t
1
,t
2
,t
3
,t
4
,t
5
},
δ(t
1
) = (student :: t
2
)
∗
,
δ(t
2
) = (supervisor :: t
3
)
?
k (takes :: t
4
)
+
k (tel :: t
5
|email :: t
5
),
δ(t
3
) = (teaches :: t
4
)
+
,
δ(t
4
) = δ(t
5
) = ε
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
286

Figure 4: Query q and its answer over G.
(t
5
corresponds to string type). Here, consider S and
the graph G in Fig. 3. In RBE, a :: t matches an edge
e if e is labeled by a and the target node of e is of type
t. Thus we can verify that G is a valid graph of S.
ShEx has two semantics of typing: single-type
typing and multi-type typing (Staworko et al., 2015).
First, a single-type typing (s-typing) of G w.r.t. S is a
function λ : V → Γ that associates every node v ∈ V
with a type λ(v). Let
out-lab-type
λ
G
(v) = {|a :: λ(v) | (v, a, v
0
) ∈ E|},
where {|···|} denotes a bag. Then λ is a
valid s-typing if for every node v ∈ V , λ(v)
matches out-lab-type
λ
G
(v). Second, a multi-type
typing (m-typing) of G w.r.t. S is a function λ :
V → 2
Γ
that associates every node v ∈ V with
a set of types λ(v). Let Out-lab-type
λ
G
(v) =
L(Flatten(out-lab-type
λ
G
(v))). For example, if
out-lab-type
λ
G
(v)) = {|a :: {t
1
,t
2
}, b :: {t
3
}|}, then
Out-lab-type
λ
G
(v)) = {{|a :: t
1
, b :: t
3
|}, {|a :: t
2
, b ::
t
3
|}}. Then an m-typing λ is valid if
1. λ(v) 6=
/
0 for every v ∈ V , and
2. for every v ∈ V and every t ∈ λ(v),
Out-lab-type
λ
G
(v)) ∩ δ(t) 6=
/
0.
G is valid w.r.t. S under single-type (multi-type) se-
mantics if there is a valid s-typing (m-typing) of G
w.r.t. S.
3 DETECTING UNSATISFIABLE
QUERY
To determine if a query q is unsatisfiable under a ShEx
schema S, our algorithm checks if each node in q is
safely matched by a type of S. To do this, we treat S
as a graph, called schema graph. In the following, we
first define schema graph and then present our algo-
rithm.
3.1 Schema Graph
Let S = (Σ, Γ, δ) be a ShEx schema. Then the
schema graph of S is denoted by a 4-tuple G
S
=
(V
S
, E
S
,C
or
,C
int
), where V
S
= Γ is a set of nodes
(types), E
S
= {(t, l, t
0
) | δ(t) includes l :: t
0
} is a set
of edges, C
or
is a collection of sets of “disjunctive”
edges, and C
int
is a collection of sets C
[n,m]
of edges
associated with interval [n, m]. For example, con-
sider the ShEx schema S presented in the previous
section. Then Fig. 5 shows the schema graph G
s
=
(V
s
, E
s
,C
or
,C
int
= {C
∗
,C
+
,C
?
}) of S, where
V
S
= {t
1
,t
2
.t
3
,t
4
,t
5
},
E
S
= {(t
1
, student,t
2
), (t
2
, supervisor, t
3
),
(t
2
, takes, t
4
), (t
2
, tel, t
5
), (t
2
, email, t
5
),
(t
3
, teaches, t
4
)},
C
or
= {{(t
2
, tel, t
5
), (t
2
, email, t
5
)}},
C
∗
= {(t
1
, student,t
2
)},
C
+
= {(t
2
, takes,t
4
), (t
3
, teaches,t
4
)},
C
?
= {(t
2
, supervisor,t
3
)}.
Figure 5: Schema graph of S.
Under s-type semantics, our algorithm uses the
schema graph defined above. On the other hand, un-
der m-typing semantics we need some modification to
the schema graph, since some nodes may be associ-
ated with more than one type. To handle this, we cre-
ate new types representing “combined types.” Here,
we briefly explain this by an example. For types t
1
and t
2
, the combined type of t
1
and t
2
, denoted t
12
, is
obtained as follows.
1. Find the common part of δ(t
1
) and δ(t
2
) without
taking care of target type. For example, let δ(t
1
) =
a :: t
3
|b :: t
4
and δ(t
2
) = a :: t
2
. Then we obtain
a :: t
3
from δ(t
1
) and a :: t
2
from δ(t
2
) since “a” is
the common label. If the result is empty, t
12
is not
created.
2. For each corresponding “label::type” pair in δ(t
1
)
and δ(t
2
), combine the target types of the “la-
bel::type” pair. In this example, since a :: t
3
of
Detecting Unsatisfiable Pattern Queries under Shape Expression Schema
287

δ(t
1
) corresponds to a :: t
2
of δ(t
2
), the target types
t
2
and t
3
are combined and we obtain δ(t
12
) = a ::
t
23
.
3. Each edge incident to t
1
or t
2
is “copied” for t
12
,
e.g., if there is an edge (t, l,t
1
), then we also have
(t, l, t
12
).
To summarize, under m-typing semantics we firstly
obtain all the combined types as above, add the com-
bined types and the “copied” edges incident to the
combined types to S, and then apply our algorithm
to the modified schema of S. Note that t
1
can be
combined with t
2
only if δ(t
1
) and δ(t
2
) are “enough
close” to each other in that a node v of type t
1
is also
of t
2
. Thus, in general the number of such combined
types generated from a ShEx schema would be rather
small.
3.2 Algorithm
Basically, our algorithm is based on solving the sub-
graph isomorphism problem between query q and
schema graph of S. However, existing methods for
solving the problem cannot be applied to our prob-
lem due to the following reasons. First, the schema
graph may contain disjunction, and thus edges in the
same set of C
or
cannot be matched at the same time.
Second, RBE may contain intervals, which imposes
an upper bound on the number of outgoing edges
and thus such a restriction needs to be taken into ac-
count when finding a match between edges of q and S.
Third, more than one query node may have the same
type; thus, the mapping from pattern nodes to schema
types may not be bijective.
Our algorithm consists of two parts: Algo-
rithms 3.1 and 3.2. Algorithm 3.1 is the initialization
part of our algorithm and Algorithm 3.2 is called from
Algorithm 3.1 to find a match between q and S. First,
Algorithm 3.1 works as follows. Line 1 initializes M,
which is a set to store “answer”, i.e., a set of pairs
of matched nodes between q and schema graph G
S
.
MAKESCHEMAGRAPH on line 2 creates the schema
graph G
S
of S. Lines 3 to 6 find, for each node u of q,
a set of candidate nodes (types) C(u) ⊆ Γ. Here, C(u)
consists of “candidate” types t ∈ Γ such that the set of
outgoing labels of t includes that of u. FILTERCAN-
DIDATES on line 4 is a function that computes C(u).
On line 7, FINDMATCH recursively traverses q and
G
S
and finds “matching” between q and G
S
.
Algorithm 3.2, called FINDMATCH, recursively
traverses q and G
S
and adds matched pairs to M.
Lines 1 and 2 check whether the size of M reaches
the number of nodes of q. If it holds, then every node
in q is safely matched by a type of S and thus output
Algorithm 3.1: Unsatisfiability CHECKING.
Input: query q = (V (q), E(q)), ShEx schema S =
(Σ, Γ, δ)
Output: “satisfiable” or “unsatisfiable”
1: M
:
=
/
0;
2: G
S
= MAKESCHEMAGRAPH(S);
3: for each u ∈ V (q) do
4: C(u)
:
= FILTERCANDIDATES(q, G
S
, u);
5: if C(u) =
/
0 then
6: return “unsatisfiable”;
7: FINDMATCH(q, G
S
, M, nil)
Algorithm 3.2: FINDMATCH.
Input: query q = (V (q), E(q)), schema graph G
S
=
(Γ, E
S
,C
or
,C
int
), set M ⊆ V (q) × Γ, current node
u
c
Output: “satisfiable” or “unsatisfiable”
1: if |M| = |V (q)| then
2: return “satisfiable”;
3: else
4: u
:
= NEXTVERTEX(q, u
c
);
5: E
u
← {(u, l, u
0
) ∈ E(q) | u
0
appears in M}
∪ {(u
0
, l, u) ∈ E(q) | u
0
appears in M}
6: E
t
← {(t, l, t
0
) ∈ E
S
| t
0
appears in M}
∪ {(t
0
, l,t) ∈ E
S
| t
0
appears in M}
7: for each t ∈ C(u) such that t is not in M do
8: if CHECKDISJUNCTION(u, t, q, G
S
, E
u
, E
t
)
then
9: if ISUSABLEONCE(u, t, q, G
S
, E
u
, E
t
)
then
10: if ISUSABLENTIMES(u, t, q, G
S
,E
u
,E
t
)
then
11: UPDATESTATE(M, u,t);
12: FINDMATCH(q, G
S
, M, u);
13: RESTORESTATE(M, u, t);
14: return “unsatisfiable”;
“satisfiable”. NEXTVERTEX on line 4 is a function
that returns the “next” node u ∈ V(q) of the current
node u
c
. If u
c
= nil, then the function returns the first
node of q. Here, we assume that there is some order
on V (q) (the order can be arbitrary), and NEXTVER-
TEX works based on that order. Lines 7 to 10 deter-
mine, for each candidate t ∈ C(u), whether t matches
u w.r.t. M. Let E
u
be the set of edges between u and
the q’s nodes in M, and let E
t
be the set of edges be-
tween t and the G
S
’s nodes in M. Checking if t safely
matches u is done by the following three functions.
1. CHECKDISJUNCTION on line 8 checks if t can
match u without violating the disjunction con-
straints in S. This is done by comparing E
u
and
E
t
along with C
or
of S. For example, if t has ex-
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
288

actly two outgoing edges (t, a, t
0
) and (t, b, t
00
) that
are in the same set of C
or
while u has two outgo-
ing edges (u, a, u
0
) and (u, b, u
00
) such that t
0
(t
00
)
matches u
0
(resp., u
00
), then t cannot match u.
2. ISUSABLEONCE on line 9 checks if t can match u
without violating the constraints on the edge car-
dinality of q except C
int
. That is, if an edge inci-
dent to t does not appear in C
int
, then the corre-
sponding edge incident to u must be exist at most
once. The function checks if the condition holds
for u and t.
3. ISUSABLENTIMES on line 10 checks if t can
match u without violating C
int
. For example, sup-
pose that (t, a, t
0
) ∈ C
[0,k]
. Then the number of
edges in E
u
that match (t, a, t
0
) must be no more
than k. The function checks such a condition by
comparing E
u
and E
t
along with C
int
.
If all the above checks are passed, then pair (u, t) is
added to M by UPDATESTATE on line 11. On line 12,
call FINDMATCH recursively in order to find matches
for the rest of nodes of q and G
S
. If no answer is found
by the call of FINDMATCH, then RESTORESTATE on
line 13 restores M, i.e., (u, t) is deleted from M, and
back to line 7. Finally, if no answer is found until all
the nodes in q are examined, output “unsatisfiable” on
line 14.
Finally, consider briefly the computational com-
plexity of the problem. In theory, the problem cannot
be solved efficiently.
Theorem 1. Detecting unsatisfiable pattern queries
is NP-hard under both s-typing and m-type semantics.
The algorithm checks if each node u of q is
matched by a node t of S. Thus the time complex-
ity may become exponential in the worst case, but
which is unavoidable due to the above theorem. How-
ever, the size of schema is much smaller than that of
data graph, and the algorithm terminates as soon as
one satisfiable matching is found. Thus, although the
problem is NP-hard, the algorithm can be executed
highly efficiently as shown in the next section.
4 PRELIMINARY EXPERIMENTS
We conducted preliminary experiments to evaluate
our algorithm. To detect unsatisfiable queries, the al-
gorithm has to be executed before executing queries
over RDF data. Therefore, we need to verify that
the execution time of our algorithm is enough small
compared with query execution time over RDF data.
The algorithm was implemented in Ruby 2.5.1, and
all the experiments were executed on a machine with
Intel(R) Core(TM) m3-7Y30 CPU 1.60GHz, 4.00GB
RAM, Windows 10 Home OS.
We used two datasets. The first one was gener-
ated by SP
2
Bench (Schmidt et al., 2008) and the sec-
ond one was generated by BSBM (Bizer and Schultz,
2009). SP
2
Bench is a well-known SPARQL per-
formance benchmark tool based on DBLP. For the
SP
2
Bench dataset, we generated RDF data of size
1,087,517 byte (10,291 triples) and 5,400,376 byte
(50,168 triples). Since SP
2
Bench does not have any
ShEx schema, we manually created a ShEx schema
(type: 11, edge: 69) based on (Schmidt et al., 2008).
BSBM is also a well-known SPARQL performance
benchmark tool, which data is based on e-commerce
use case. For the BSBM dataset, we generated
RDF data of size 2,583,293 byte (10,250 triples) and
10,216,303 byte (40,377 triples). BSBM does not
have any ShEx schema either, therefore we created a
ShEx schema (node: 10, edge: 71) based on (Bizer
and Schultz, 2009). Since both of SP
2
Bench and
BSBM assume s-type semantics implicitly, the exper-
iments were conducted under s-typing semantics.
As for pattern queries, we made a Ruby program
for generating queries. In short, this program ran-
domly selects labels and types from a given ShEx
schema and generates nodes and edges, and then the
authors check unsatisfiability of the generated queries
manually. We generated 50 different unsatisfiable
queries (10 queries for each of 5 different query
sizes) for each dataset. We also made a Ruby pro-
gram to execute queries based on the Ullmann’s algo-
rithm (Ullmann, 1976). Note that, although a num-
ber of algorithms for pattern matching are proposed,
the data used in this experiments are very small and
thus which algorithm is used hardly affects execu-
tion time. Actually, in such a case “preprocessing”
such as reading data and registering nodes and edges
into lists/arrays accounts for most portion of execu-
tion time, which is common to any kind of pattern
matching algorithms.
Tables 1 and 2 show the results. All the execu-
tion times were measured in seconds. Each query ex-
ecution time in the tables is the average of those of
10 queries. As shown in the tables, compared with
the query execution time over RDF data, the execu-
tion time of our algorithm is much smaller and, e.g.,
we can save about 300 seconds for the larger data of
SP
2
Bench dataset. Also, the ratio values are almost
negligible. Note that, since the size of RDF data used
in the experiment is rather small, the ratio would be-
come much smaller if we use larger RDF data. There-
fore, if a user tries to execute a query and it is unsatis-
fiable, our algorithm can save a lot of time by detect-
ing the unsatisfiability of the query. And even if it is
Detecting Unsatisfiable Pattern Queries under Shape Expression Schema
289
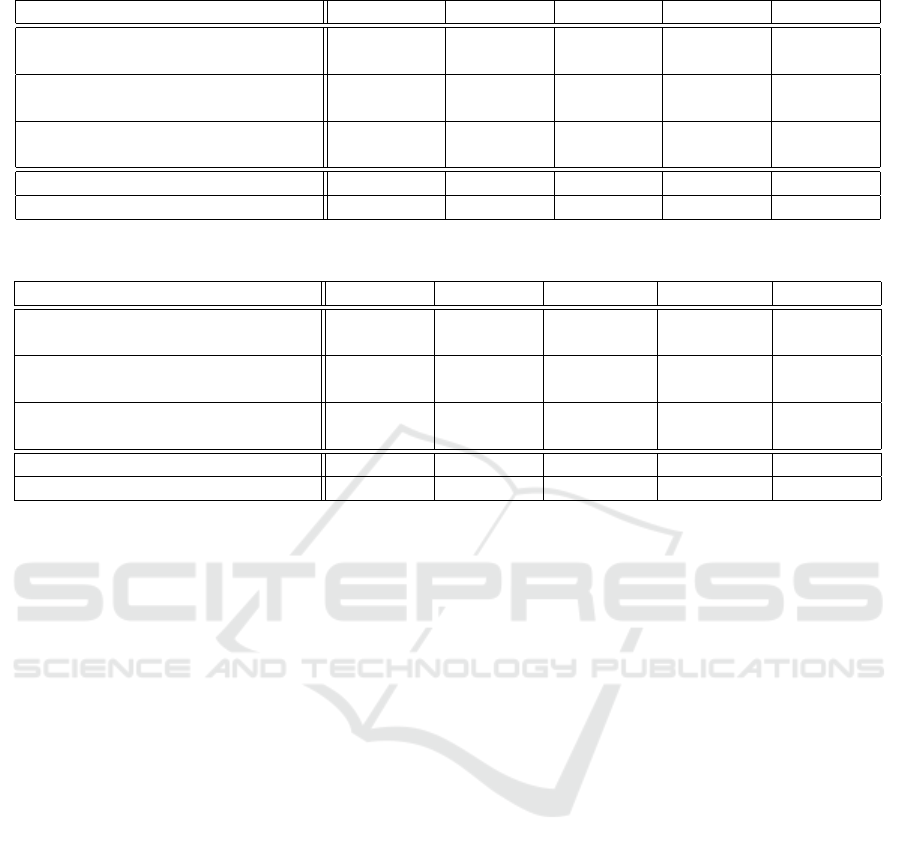
Table 1: Result for SP2Bench dataset.
query size 3 4 5 6 7
(a) Unsatisfiability Checking time
(our algorithm)
0.00343 0.00357 0.00501 0.00463 0.00469
(b) Query execution time
(10,291 triples)
43.2 34.1 34.1 36.0 38.9
(c) Query execution time
(50,168 triples)
369 343 396 406 339
Time ratio (a/b) 0.0000793 0.000105 0.000147 0.000129 0.000120
Time ratio (a/c) 0.00000927 0.0000104 0.0000126 0.0000114 0.0000138
Table 2: Result for BSBM dataset.
query size 3 4 5 6 7
(a) Unsatisfiability checking time
(our algorithm)
0.0105 0.00737 0.00888 0.0114 0.00762
(b) Query execution time
(10,250 triples)
18.1 15.5 19.9 23.5 17.6
(c) Query execution time
(40,377 triples)
224 216 236 230 238
Time ratio (a/b) 0.000574 0.000475 0. 000446 0.000486 0. 000433
Time ratio (a/c) 0.0000469 0.0000342 0. 0000377 0. 0000497 0.0000321
satisfiable, unsatisfiability checking can be done very
quickly and little time is wasted.
5 CONCLUSIONS
In this paper, we proposed an algorithm for detect-
ing unsatisfiable pattern queries under ShEx schemas.
Experimental results suggest that our algorithm run
efficiently w.r.t. the running time of query execution.
As future issues, since the experiments were con-
ducted under s-type semantics only, we need to con-
duct experiments under m-typing semantics. We also
need to use other datasets under variety kinds of of
ShEx schemas. Moreover, ShEx has more functions
not discussed in this paper (e.g., negation). Thus we
need to consider extending our algorithm to adopt
such functions.
REFERENCES
Baker, T. and Prud’hommeaux, E. (2019).
Shape expressions (ShEx) primer.
http://shexspec.github.io/primer/.
Benedikt, M., Fan, W., and Geerts, F. (2008). XPath satis-
fiability in the presence of DTDs. J. ACM, 55(2):8:1–
8:79.
Bizer, C. and Schultz, A. (2009). The berlin SPARQL
benchmark. In International journal on Semantic Web
and information systems 5(2), pages 1–24.
Cristani, M., Bertolaso, A., Scannapieco, S., and Tomaz-
zoli, C. (2018). Future paradigms of automated pro-
cessing of business documents. International Journal
of Information Management, 40:67–75.
Figueira, D. (2018). Satisfiability of XPath on data trees.
ACM SIGLOG News, 5(2):4–16.
Geneves, P., Layada, N., and Knyttl, V. (2011). XML
reasoning solver user manual. available from
https://hal.inria.fr/inria-00339184v2/document.
Groppe, J. and Groppe, S. (2007). Filtering unsatisfi-
able XPath queries. Data & Knowledge Engineering,
64(1):134–169.
Ishihara, Y., Suzuki, N., Hashimoto, K., Shimizu, S., and
Fujiwara, T. (2013). XPath satisfiability with parent
axes or qualifiers is tractable under many of real-world
DTDs. In Proceedings of the 14th International Sym-
posium on Database Programming Languages (DBPL
2013).
Montazerian, M., Wood, P. T., and Mousavi, S. R. (2007).
XPath query satisfiability is in PTIME for real-world
DTDs. In Proc. International XML Database Sympo-
sium, pages 17–30.
Schmidt, M., Hornung, T., Lausen, G., and Pinkel, C.
(2008). SP2Bench: a SPARQL performance bench-
mark. In Proc. ICDE, pages 371–393.
Staworko, S., Boneva, I., Labra Gayo, J. nad Hym, S.,
Prud’hommeaux, E., and Sorbrig., H. (2015). Com-
plexity and expressiveness of ShEx for RDF. In
Proceedings of 18th In-ternational Conference on
Database Theory (ICDT 2015), pages 195–211.
Thornton, K., Solbrig, H., Stupp, G. S., Labra Gayo, J. E.,
Mietchen, D., Prud’hommeaux, E., and Waagmeester,
A. (2019). Using shape expressions (ShEx) to share
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
290

RDF data models and to guide curation with rigorous
validation. In Hitzler, P., Fernandez, M., Janowicz,
K., Zaveri, A., Gray, A. J., Lopez, V., Haller, A., and
Hammar, K., editors, In Proceedings of the European
Semantic Web Conference, pages 606–620.
Ullmann, J. R. (1976). An algorithm for subgraph isomor-
phism. Journal of the ACM, 23(1):31–42.
Zhang, X., den Bussche, J. V., and Picalausa, F. (2016). On
the satisfiability problem for SPARQL patterns. Jour-
nal of Artificial Intelligence Research, 55:403–428.
Detecting Unsatisfiable Pattern Queries under Shape Expression Schema
291
