Transforming Property Path Query
According to Shape Expression Schema Update
Goki Akazawa
∗
, Naoto Matsubara
†
and Nobutaka Suzuki
‡
University of Tsukuba, Tsukuba, Japan
Keywords:
ShEx, Property Path, Schema Update.
Abstract:
Suppose that we have a query q under schema S and then S is updated. Then we have to update q according
to the update of S, since otherwise q no longer reports correct answer. However, updating q manually is often
a difficult and time-consuming task since users do not fully understand the schema definition or are not aware
of the details of schema update. In this paper, we consider transforming queries automatically according to
schema update. We focus on Shape Expression (ShEx) and Property Path as schema and query language,
respectively, and we take a structural approach to transform Property Path query. For a Property Path query q
and a schema update op to an ShEx schema S, our algorithm checks how op affects the structure of q under S,
and transforms q according to the result.
1 INTRODUCTION
Schema plays an important role in management of
various kinds of data, and the importance holds for
RDF/graph data as well. Since user requirements to
RDF data may change over time, schema tends to be
updated continuously to meet the requirements. Here,
suppose that we have a query q written for data under
schema S, then S is updated, and that q is (re)executed
after the update. Such a situation often arises, e.g., (a)
q is embedded in a program code and the code is ex-
ecuted after a schema update, (b) q is recorded in a
user’s history and she/he tries to use q again, and so
on. In such cases, we have to update q according to
the update of S, since otherwise q no longer reports
correct answer. However, updating q manually is of-
ten a difficult and time-consuming task, since users do
not fully understand the schema definition or are not
aware of the details of schema update.
To address the problem, in this paper we con-
sider transforming queries automatically according
to schema update. We focus on Shape Expression
(ShEx) (Baker and Prud’hommeaux, 2019) and Prop-
erty Path as schema and query language, respectively.
Here, ShEx is a novel schema language for RDF and
is already used in a number of areas (Thornton et al.,
2019). For RDF data, there is another schema lan-
guage, called SHACL (Knublauch and Kontokostas,
2017), but it has some differences. SHACL schema
description tends to be more complicated due to its
strict definition. On the other hand, ShEx has higher
readability and is easy to handle although the vocab-
ulary has some limitation. In addition, recursion is
formally supported in the ShEx specification, but not
in that of SHACL (depending on the implementation).
As for query language, Property Path is a well-known
path query language included in SPARQL 1.1. In
this paper, we first define update operations to ShEx
schema, then propose an algorithm for transforming
a given query into a new query according to schema
update.
In this paper we take a structural approach to
transform query. For a query q and an update oper-
ation(s) op to ShEx schema S, our algorithm checks
how op affects the structure of S, examines how the
changes to S affects the structure of q, and then trans-
forms q into new query q
0
according to the result.
Here, it is desirable that the transformed query q
0
pre-
serves the behaviour of q as much as possible, i.e.,
the answer of q
0
should be as close to that of its origi-
nal query q as possible. To examine the effectiveness
of our structural approach, we made a small prelimi-
nary experiment. The result suggests that transformed
queries obtained by our algorithm show rather good
behaviors on this respect.
1.1 Related Work
For XML documents, a number of studies on schema
updates have been made so far. Guerrini et al. pro-
292
Akazawa, G., Matsubara, N. and Suzuki, N.
Transforming Property Path Query According to Shape Expression Schema Update.
DOI: 10.5220/0010173002920298
In Proceedings of the 16th International Conference on Web Information Systems and Technologies (WEBIST 2020), pages 292-298
ISBN: 978-989-758-478-7
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

posed update operations that assures any updated
schema contains its original schema so that docu-
ments under an original schema remains valid under
its updated schema (Guerrini et al., 2005). Junedi et
al. studied query-update independence analysis and
showed that the performance of (Benedikt and Ch-
eney, 2010) can be drastically enhanced in the use of
µ-calculus (Junedi et al., 2012). Oliveira et al. pro-
posed an algorithm for detecting possible problems
affecting XQuery code according to XML Schema
update (Oliveira et al., 2012). Wu et al. proposed
an algorithm for correcting XSLT stylesheet accord-
ing to DTD update (Wu and Suzuki, 2016).
For RDF/graph schema update, Chirkova and
Fletcher proposed a model of RDF schema evolu-
tion (Chirkova and Fletcher, 2009) but no query trans-
formation was considered. Bonifati et al. discussed
evolution of property graph schema by using graph
rewriting operations (Bonifati et al., 2019).
To the best of our knowledge, however, no stud-
ies on transforming Property Path query according to
ShEx schema update have been made so far.
The rest of this paper is organized as follows. Sec-
tion 2 gives some preliminary definitions. Section 3
shows some operations to types of ShEx schema and
our algorithm. Section 4 presents the result of our pre-
liminary evaluation experiment. Section 5 shows our
conclusion.
2 PRELIMINARIES
Let Σ be a set of labels. A labeled directed graph
(graph for short) is denoted G = (V, E), where V is a
set of nodes and and E ⊆ V × Σ ×V is a set of edges.
Let e ∈ E be an edge labeled by l ∈ Σ from a node
v ∈ V to a node v
0
∈ V . Then e is denoted (v, l, v
0
), v is
called source, and v
0
is called target.
Unlike XML documents, in RDF/graph data the
order among sibling nodes are less significant. Thus
ShEx uses regular bag expression (RBE) to represent
content model of type (Staworko et al., 2015). RBE
is defined similarly to regular expression except that
RBE uses unordered concatenation instead of ordered
concatenation. Let Γ be a set of types. Then RBE over
Σ × Γ is recursively defined as follows.
• ε and a :: t ∈ Σ × Γ are RBEs.
• If r
1
, r
2
, · ·· , r
k
are RBEs, then r
1
|r
2
|· ·· |r
k
is an
RBE, where | denotes disjunction.
• If r
1
, r
2
, · ·· , r
k
are RBEs, then r
1
k r
2
k ·· · k r
k
is
an RBE, where k denotes unordered concatena-
tion.
• If r is an RBE, then r
[n,m]
is an RBE, where n ≤ m.
In particular, r
?
= r
[0,1]
, r
∗
= r
[0,∞]
, and r
+
= r
[1,∞]
.
For example, let r = a :: t
1
k (b :: t
2
|c :: t
3
) be an RBE.
Since k is unordered, r matches not only a :: t
1
b :: t
2
and a :: t
1
c :: t
3
but also b :: t
2
a :: t
1
and c :: t
3
a :: t
1
.
A ShEx schema is denoted S = (Σ, Γ, δ), where
Γ is a set of types and δ is a function from Γ to
the set of RBEs over Σ × Γ. For example, let S =
(Σ, Γ, δ) be a ShEx schema, where Σ = {a, b, c}, Γ =
{t
0
, t
1
, t
2
, t
3
, t
4
}, and
δ(t
0
) = a :: t
1
k b :: t
3
k (c :: t
2
)
∗
,
δ(t
1
) = b :: t
3
|c :: t
4
,
δ(t
2
) = c :: t
3
,
δ(t
3
) = ε,
δ(t
4
) = a :: t
3
.
For example, consider the graph G shown in
Fig. 1(left). In RBE, a :: t matches an edge e if the
label of e is a and the target node of e is of type t.
Thus, assuming that each node v
i
is of type t
i
, δ(t
i
)
matches the outgoing edges of v
i
. Then it is easy to
verify that G is a valid graph of S.
The schema graph of a ShEx schema S =
(Σ, Γ, δ) is a graph G
S
= (V
S
, E
S
), where V
S
= Γ and
E
S
= {(t, a, t
0
) | δ(t) contains a :: t
0
}. For example,
Fig. 1(right) shows the schema graph of S.
Property Path query (query for short) over Σ is de-
fined as follows.
• ε and any a ∈ Σ is a query. Here, query a matches
an edge labeled by a.
• ∗ is a “wildcard” query, which matches any edge.
• For a set of labels {a
1
, a
2
, · ·· , a
k
},
!{a
1
, a
2
, · ·· , a
k
} is a query. Here, ! denotes
negation and this query matches an edge whose
label is not in {a
1
, a
2
, · ·· , a
k
}.
• For a label a ∈ Σ, a
−1
is a query, which matches
the inverse of an edge labeled by a.
• For queries q
1
, q
2
, · ·· , q
k
, q
1
.q
2
. · ·· .q
k
and
q
1
|q
2
|· ·· |q
k
are queries. The former matches a
path p = p
1
. p
2
. · ·· . p
k
if q
i
matches subpath p
i
for
every 1 ≤ i ≤ k. The latter matches a path p if one
of q
1
, q
2
, · ·· , q
k
matches p.
• For a query q, q
∗
is a query. This query matches a
path p = p
1
. p
2
. · ·· . p
k
if q matches subpath p
i
for
every 1 ≤ i ≤ k (k ≥ 0).
In this paper, we focus on single source query traver-
sal. For a graph G, query q, and node v
s
, the answer
of q from v
s
over G is a set of nodes v such that G
contains a path from v
s
to v whose sequence of labels
is matched by q. For example, if q = a
−1
.!{a, b}, then
the answer of q from v
1
over G in Fig.1 is {v
2
}.
Transforming Property Path Query According to Shape Expression Schema Update
293

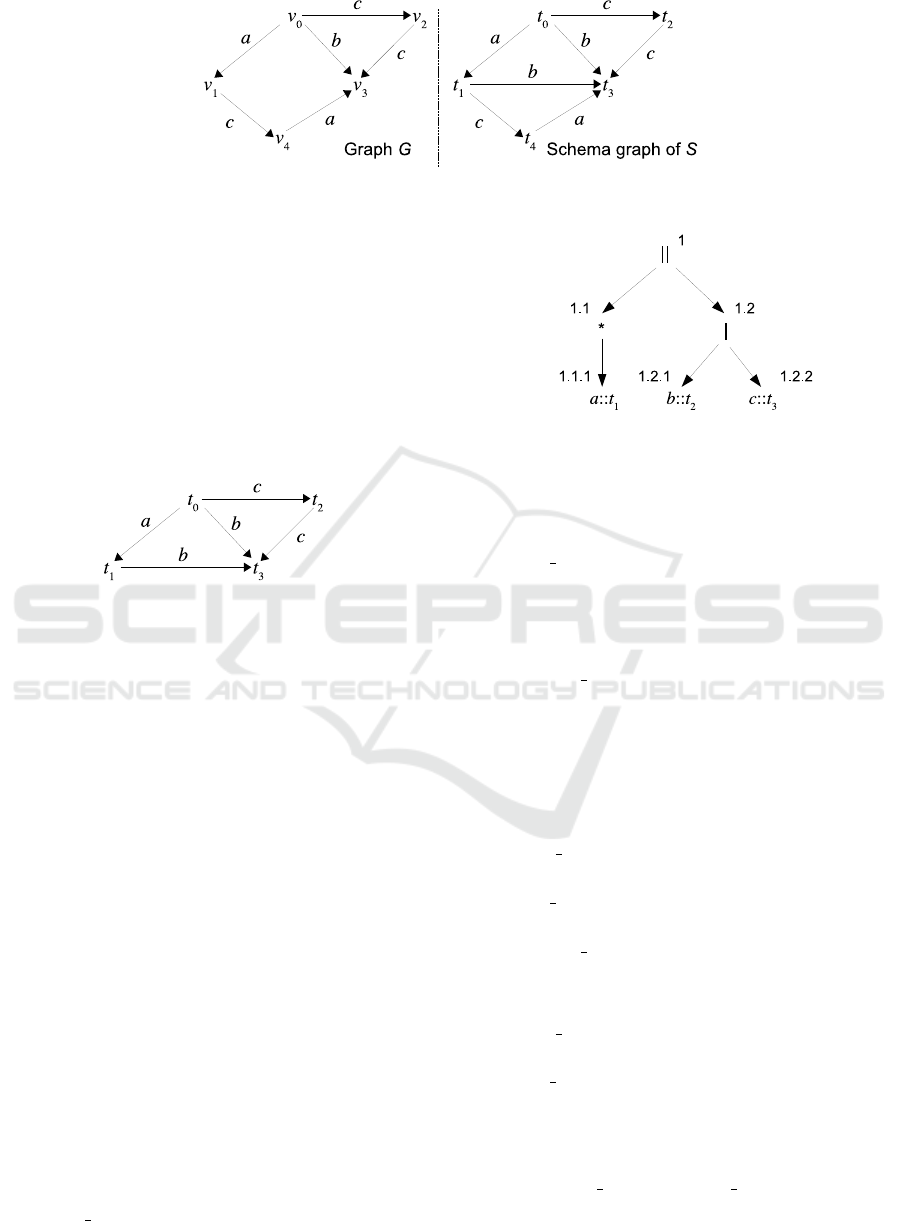
Figure 1: Valid graph G and schema graph of S.
Let G
S
= (V
S
, E
S
) be the schema graph of S, q
be a query, and t be a type of S. By G
S
(q, t) we
mean the traversal area of q from t over G
S
, that is,
the subgraph of G
S
traversed by q from t over G
S
.
For example, let G
S
be the schema graph shown in
Fig. 1(right), q = b.(c
−1
)
∗
.(a|b). Then G
S
(q, t
1
) is
shown in Fig. 2. By Ans(G
S
(q, t)), we mean the “an-
swer” types of G
S
(q, t)), i.e., the “answer” types ob-
tained by traversing q from t over G
S
. For example,
in Fig. 2 Ans(G
S
(q, t
1
)) = {t
1
, t
3
}.
Figure 2: Traversal area G
S
(q, t
1
).
3 QUERY TRANSFORMATION
In this section, we first define operations to types
of ShEx schema. Then we present an algorithm for
transforming a given query according to schema up-
date.
3.1 Operation on Types
To represent schema update, we introduce update op-
erations (operations for short) to types. First, we in-
troduce tree representation of type. To identify the
position of each node, an id based on Dewey ordering
is given to each node. For example, let
δ(t
0
) = a :: t
∗
1
k (b :: t
2
|c :: t
3
).
Then the tree representation of t
0
is shown in Fig. 3.
The id associated with each node is the position of the
node.
We define the following eight operations to types
of ShEx schema. Let t be a type of a ShEx schema S.
• Changing label::type pair of type:
– add
l t(t, i, l
0
:: t
0
): this operation adds la-
bel::type pair l
0
:: t
0
to δ(t) at position i, where
Figure 3: Tree representation of t
0
.
i is a Dewey order. This operation corresponds
to adding an edge (t, l
0
, t
0
) to the schema graph
of S.
– del lt(t, i): this operation deletes label::type
pair at position i of δ(t). Let l
0
:: t
0
be the pair
to be deleted. Then this operation corresponds
to deleting an edge (t, , t
0
, l
0
) from the schema
graph of S.
– change lt(t, i, l
0
:: t
0
): this operation replaces la-
bel::type pair at position i of δ(t) with l
0
:: t
0
.
Let l
00
:: t
00
be the pair to be replaced. Then
this operation corresponds to replacing an edge
(t, l
00
, t
00
) with an edge (t, l
0
, t
0
) in the schema
graph of S.
• Changing operator (|, k, [n, m]) of type:
– add opr(t, i, op): this operation adds an opera-
tor op to to δ(t) at position i.
– del opr(t, i): this operation deletes the opera-
tion at position i from δ(t).
– change opr(t, i, op): this operation replaces the
operation at position i of δ(t) with op.
• Adding/deleting type of schema:
– add type(t): this operation adds a new type t
to S. Initially, δ(t) = ε.
– del type(t): this operation deletes type t from
S.
An update script is a sequence s = op
1
op
2
·· ·op
n
of
operations. For example, consider t
0
in Fig. 3 and let
s = change lt(t
0
, 1.2, k)add lt(t
0
, 1.1, d :: t
3
)
be an update script. By applying s to t
0
, we obtain
δ(t
0
) = d :: t
3
k a :: t
∗
1
k (b :: t
2
k c :: t
3
).
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
294

Let q be a query and S be a ShEx schema. In
the above operations, add lt(), add opr(), del opr(),
change opr(), add type() do not affect q in that q
remains “valid” against the update schema of S. On
the other hand, del lt(), change lt(), del type() may
affect q, i.e., q may become “invalid” under the up-
dated schema of S in that q may lost some part of
answers that were obtained under S. Thus, our al-
gorithm shown below transforms q when del lt(),
change lt(), or del type() is applied to S.
We finally note that when a ShEx schema S is up-
dated, the data under S must also be updated accord-
ing to the schema update. Thus we have developed a
method for updating data according to schema update
(details are omitted).
3.2 Algorithm
Our algorithm consists of Algorithms 1 and 2. Algo-
rithm 1 is the main part of our algorithm. For a given
update script s = op
1
.op
2
. · ·· .op
n
on ShEx schema
S and start type t
s
, the algorithm transforms a given
query q according to s. Let G
S
be the schema graph
of S, and let G
S
(q, t
s
) be the traversal area of q from
t
s
(lines 1 and 2). First, we take copies H
S
and G
0
S
of
G
S
(q, t
s
) and G
S
, respectively (line 3). Then for each
operation op
i
of s the algorithm modifies H
S
accord-
ing to op
i
(lines 4 to 27), and converts H
S
to trans-
formed query q
0
(line 28). The for loop in lines 4 to
27 proceeds as follows. The algorithm does nothing
if op
i
does not affect the traversal area H
S
(lines 5 to
7). Otherwise, H
S
(and G
0
S
) is modified according to
op
i
in lines 8 to 26, as follows.
• Lines 8 to 14 deal with change lt(t, i, l
0
:: t
0
). This
operation changes label::type pair l
i
:: t
i
of δ(t) at
position i to l
0
:: t
0
. According to this, we replace
edge (t, l
i
, t
i
) with (t, l
0
, t
0
) in H
S
and G
0
S
. If t
i
= t
0
,
then we are done. Otherwise, since t
i
is changed
to t
0
, a path from t
s
to some accepting node via
t
i
may be disconnected by this change. To repair
this, we find a set of simple paths P from t
0
to t
i
in
G
0
S
by FindPaths and add each path p ∈ P to H
S
to
connect t
i
and t
0
.
Here, for given types t, t
0
, FindPaths (not shown)
is a method for finding the set P of simple paths
p from t to t
0
over G
0
S
with inverse edge traversal
allowed. But if the length of every simple path
p exceeds a given threshold, FindPaths also tra-
verses paths from t to the neighbours of t
0
and if
shorter simple path(s) is found, then the FindPaths
reports the shorter paths instead of P.
• Lines 15 to 19 deal with del lt(t, i). This opera-
tion deletes the label::type pair l
i
:: t
i
at position i
of δ(t). According to this, we delete edge (t, l
i
, t
i
)
from H
S
and G
0
S
. By this edge deletion t and t
i
may be disconnected, thus we find paths from t to
t
i
over G
0
S
by FindPaths and add the paths to H
S
.
• Lines 20 to 26 deal with del type(t). This opera-
tion deletes type t from S. Thus t and every edge
incident to t is deleted from H
S
and G
0
S
. To repair
this, we find the set T
s
of nodes outgoing to t and
the set T
g
of nodes incoming from t, and then find
paths from T
s
to T
g
and add the paths to H
S
.
In line 28, ConstructPropertyPath (Algorithm 2) con-
verts H
S
to new query q
0
. This is done by regard-
ing H
S
as an NFA M with start state t
s
and the set
Ans(G
S
(q, t
s
)) of accept states (line 2), constructing a
DFA M
0
equivalent to M (line 3), and then converting
M
0
into a query q
0
(line 4). The conversion from M
0
to q
0
is done by using an extension of the state elimi-
nation method for DFA.
4 PRELIMINARY EXPERIMENT
In this section, we present the result of our prelimi-
nary evaluation experiment. We applied our algorithm
to several queries in order to examine if the trans-
formed queries show “good” behaviour in the sense
that the answers of the original queries are maintained
after schema update.
The data used in this experiment is Japanese Text-
book LOD (Egusa and Takaku, 2018a; Egusa and
Takaku, 2018b). Here, Japanese Textbook LOD is
RDF data compiled from a collection of textbooks
that has been organized over the years by NIER Edu-
cation Library and Textbook Research Center Library.
The data structure of Japanese Textbook LOD is illus-
trated in Fig. 4. Japanese Textbook LOD consists of
233,001 triples of the Turtle format. The data size is
12MB.
In this experiment, we manually created five
queries and short schema updates shown in Table. 1.
We transformed each query by the algorithm (and the
data is also transformed according to the schema up-
date), executed the original and transformed queries
over the original and updated data, respectively, and
calculated the recall, precision and F-measure values.
Let q be a query, q
0
be the transformed query of q, and
Ans(q) be the set of obtained answer nodes of q. The
recall of q
0
w.r.t. q is defined as follows.
recall(q, q
0
) =
|Ans(q) ∩ Ans(q
0
)|
|Ans(q)|
.
Similarly, the precision of q
0
w.r.t. q is defined as fol-
lows.
precision(q, q
0
) =
|Ans(q) ∩ Ans(q
0
)|
|Ans(q
0
)|
.
Transforming Property Path Query According to Shape Expression Schema Update
295

Figure 4: Data structure of Japanese Textbook LOD.
Table 1: Original query and update script.
No. (a) original query and (b) update script
1
(a) catalogue.school
(b) del lt(Textbook, 6) add lt(Textbook, 1, sub jectType :: Sub jectType)
2
(a) catalogue
−1
.publisher
−1
.curriculum.hasSubjectArea.hasSubject
(b) del type(Publisher) del lt(Catalogue, 1)
3
(a) curriculum
−1
.school
(b) del lt(Textbook, 5) del type(Sub jectArea)
4
(a) (catalogue | subjectArea).school
(b) del lt(Textbook, 6) add lt(Sub jectType, 3, hasSub ject :: Sub ject)
5
(a) subjectArea
−1
.curriculum.hasSubjectArea.hasSubject.school
(b) del type(Sub ject) change lt(CurriculumGuideline, 1, version :: Version)
Table 2 lists the transformed queries for the orig-
inal queries and their recall, precision and F-measure
values. The average F-measure of the five queries
is 0.87, and thus the transformed queries showed
rather good behaviors overall. However, the first,
second, and fourth transformed queries missed some
correct answers, especially the second one. A rea-
son for this is as follows. Japanese Textbook LOD
schema contains many edges associated with “*” or
“?”. Such edges are “optional” and their correspond-
ing edge may not appear in the RDF data. There-
fore, if transformed query contains a label of such
“optional” edges, the answers obtained by the trans-
formed queries do not coincide with those of their
original queries. In the experiment, “hasSubject” of
the second query has such optional edges.
The results show some potential of our approach,
however, the queries and schema updates used in the
experiment are very limited and we need to conduct
more experiments by using more queries and update
operations. This is left as a future work.
5 CONCLUSION
In this paper, we first defined update operations to
ShEx schema, and then proposed an algorithm for
transforming a given query into a new query accord-
ing to schema update. We made a small preliminarily
experiment and the results showed that queries trans-
formed by our algorithm shows good behaviour in
that their answers were close to that of the original
queries.
However, we have to some works to do. First,
the dataset used in our experiment is limited. Thus
we need to conduct more experiments with a variety
kinds of datasets. In the experiment, each schema up-
date consists of only two update operations. However,
we need to examine schema update consisting of more
update operations in order to reflect real schema up-
date situations. Moreover, there are some ShEx ele-
ments missing in our paper, e.g., negation. Thus we
plan to consider more broader class of ShEx schema.
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
296

Table 2: Transformed Query and Recall, Precision, F-measure.
No. Transformed Query recall precision F-measure
1 publisher.catalogue.school 0.88 0.99 0.93
2 catalogue
−1
.curriculum.hasSubjectArea.hasSubject 0.70 0.50 0.59
3 curriculum
−1
.publisher
∗
.catalogue.school 1.00 1.00 1.00
4 (publisher.catalogue | subjectArea).school 0.88 0.77 0.82
5 (subjectArea
−1
.curriculum.hasSubjectArea)
∗
.subjectType
∗
.school 1.00 1.00 1.00
average of five queries 0.89 0.85 0.87
Algorithm 1: Query Transformation.
Input: ShEx schema S = (Σ, Γ, δ), update script s =
op
1
op
2
·· ·op
n
to S, query q, type t
s
∈ Γ
Output: query q
0
1: construct the schema graph G
S
of S
2: construct the traverse area G
S
(q, t
s
) of q from t
s
on G
S
3: H
S
← G
S
(q, t
s
); G
0
S
← G
S
4: for i = 1, 2, ··· , n do
5: if op
i
does not affect H
S
then
6: continue
7: end if
8: if op
i
= change lt(t, i, l
0
:: t
0
) then
9: let l
i
:: t
i
be the label::type pair at position i
of δ(t)
10: replace (t, l
i
, t
i
) with (t, l
0
, t
0
) in H
S
and G
0
S
11: if t
i
6= t
0
then
12: P ← FindPaths(G
0
S
, t
0
, t
i
)
13: add all p ∈ P to H
S
14: end if
15: else if op
i
= del lt(t, i) then
16: let l
i
:: t
i
be the label::type pair at position i
of δ(t)
17: delete (t, l
i
, t
i
) from H
S
and G
0
S
18: P ← FindPaths(G
0
S
, t, t
i
)
19: add all p ∈ P to H
S
20: else if op
i
= del type(t) then
21: T
s
←{t
1
|(t
1
,l,t) is an edge from t
1
to t in G
0
S
22: T
g
←{t
2
| (t,l,t
2
) is an edge from t to t
2
in G
0
S
23: delete t and every edge adjacent to t from H
S
and G
0
S
24: P ← {p | p ∈ FindPaths(G
0
S
, t
1
, t
2
), t
1
∈
T
s
, t
2
∈ T
g
}
25: add all p ∈ P to H
S
26: end if
27: end for
28: q
0
← ConstructPropertyPath(H
S
,t
s
, ans(G
S
(q,t
s
)))
29: return q
0
Algorithm 2: ConstructPropertyPath.
Input: traversal area H
S
, start type t
s
, set of types Ans
Output: query q
0
1: let V and E be the sets of nodes and edges of H
S
,
respectively
2: construct an NFA M = (Q, Σ, δ, t
s
, Ans), where
Q = V and δ is a transition function s.t. δ(t, a) = t
0
iff (t, a, t
0
) ∈ E
3: construct a DFA M
0
equivalent to M
4: construct a query q
0
from M
0
5: return q
0
REFERENCES
Baker, T. and Prud’hommeaux, E. (2019).
Shape expressions (ShEx) primer.
http://shexspec.github.io/primer/.
Benedikt, M. and Cheney, J. (2010). Destabilizers and in-
dependence of XML updates. Proc. VLDB Endow.,
3(1-2):906–917.
Bonifati, A., Furniss, P., Green, A., Harmer, R., Oshurko,
E., and Voigt, H. (2019). Schema validation and evo-
lution for graph databases. In Conceptual Modeling,
pages 448–456.
Chirkova, R. and Fletcher, G. H. (2009). Towards well-
behaved schema evolution. In Proc. 12th Interna-
tional Workshop on the Web and Databases (WebDB
2009).
Egusa, Y. and Takaku, M. (2018a). Building and publishing
japanese textbook linked open data. The journal of
Information Science and Technology, 68(7):361–367.
Egusa, Y. and Takaku, M. (2018b). Japanese textbook LOD.
https://jp-textbook.github.io/en/about.
Guerrini, G., Mesiti, M., and Rossi, D. (2005). Impact of
XML schema evolution on valid documents. In Proc.
WIDM, pages 39–44.
Junedi, M., Genev
`
es, P., and Laya
¨
ıda, N. (2012). XML
query-update independence analysis revisited. In
Proc. ACM DocEng’12, pages 95–98.
Knublauch, H. and Kontokostas, D. (2017).
Shapes constraint language (SHACL).
https://www.w3.org/TR/shacl/.
Oliveira, R., Genev
`
es, P., and Laya
¨
ıda, N. (2012). Toward
automated schema-directed code revision. In Pro-
Transforming Property Path Query According to Shape Expression Schema Update
297

ceedings of the 2012 ACM Symposium on Document
Engineering, DocEng ’12, page 103–106.
Staworko, S., Boneva, I., Gayo, J. E. L., Hym, S.,
Prud’hommeaux, E. G., and Solbrig, H. R. (2015).
Complexity and expressiveness of ShEx for RDF.
In Proceedings of 18th In-ternational Conference on
Database Theory (ICDT 2015), page 17p.
Thornton, K., Solbrig, H., Stupp, G. S., Labra Gayo, J. E.,
Mietchen, D., Prud’hommeaux, E., and Waagmeester,
A. (2019). Using shape expressions (ShEx) to share
RDF data models and to guide curation with rigorous
validation. In Hitzler, P., Fern
´
andez, M., Janowicz,
K., Zaveri, A., Gray, A. J., Lopez, V., Haller, A., and
Hammar, K., editors, In Proceedings of the European
Semantic Web Conference, pages 606–620.
Wu, Y. and Suzuki, N. (2016). An algorithm for correct-
ing xslt rules according to dtd updates. In Proceed-
ings of the 4th International Workshop on Document
Changes: Modeling, Detection, Storage and Visual-
ization, DChanges ’16.
WEBIST 2020 - 16th International Conference on Web Information Systems and Technologies
298