Intelligent Algorithms for Non-parametric Robot Calibration

Marija Turkovi

1,2

, Marko

Svaco

1 a

and Bojan Jerbi

1 b

Department of Robotics and Production System Automation, Faculty of Mechanical Engineering and Naval Architecture,

University of Zagreb, Ivana Lu

ca 5, Zagreb, Croatia

Department of Physics, Faculty of Science, University of Zagreb, Bijeni

cka cesta 32, Zagreb, Croatia

Keywords:

Non-parametric Robot Calibration, Neural Networks, Genetic Algorithms, Robot Precision.

Abstract:

In this paper, a novel method for non-parametric robot calibration which uses intelligent algorithms is pro-

posed. The non-parametric calibration should prove very useful, because it does not need to identify the

geometric parameters of the robot as is the case in parametric calibration. Instead, only the position measure-

ments need to be provided. This could potentially lead to a cheaper and faster calibration process which could

simplify its application on different and unique robot geometries. The biggest issue of using neural networks

is that they require a lot of data, while for the process of robot calibration a very limited number of measure-

ments is usually collected. In this experiment, the improvement of the hyperparameters of the neural network

was attempted by using the genetic algorithms. Simulations also showed that the parametric optimization

converges faster and that feed-forward back-propagating neural networks could not correctly simulate the be-

haviour of complex robots, or problems which used small datasets. However, for simple robot geometries and

massive datasets, the neural network successfully simulated the behaviour of the robot. Although the number

of measurements needed was well beyond the scope for real world applications, a few possible improvements

were suggested for future research.

1 INTRODUCTION

Robot calibration is a process which can signiﬁcantly

improve the accuracy of a robot by correcting its po-

sitioning errors. The main objective is to establish an

accurate mapping between the theoretical model of an

idealized robot and an actual measured position. The

inconsistencies in predicted and realized locations of

a robot are arising from many error sources (for exam-

ple, manufacturing tolerances, wear and tear, trans-

mission errors, compliance and set-up errors).

The most common method of calibration is para-

metric calibration, and it focuses on constructing a

model of a robot and determining the actual param-

eters of the robot, thereby improving the positioning

accuracy. This type of calibration was extensively re-

searched over the past decades and many solutions

have already been given (Gang et al., 2014). The para-

metric calibration has in most cases four basic steps.

First, the geometric model of the robot which de-

scribes the relationship between the robot joint space

and the actuator space is made. Afterwards, the ac-

https://orcid.org/0000-0002-6761-4336

https://orcid.org/0000-0003-1811-5669

tual robot locations are measured by using an exter-

nal measurement device, which is followed by param-

eter identiﬁcation based on the differences between

the measured and the expected positions. Finally, the

implementation of the modiﬁed geometric model is

made, which provides better positioning of the robot

(

Svaco et al., 2014).

In recent years, intelligent optimization tech-

niques such as neural networks and genetic algo-

rithms are increasing in popularity in a variety of ap-

plications. Genetic algorithms were inspired by the

process of evolution and there are many approaches

in the calibration techniques which are making use

of genetic programming to minimize the difference in

the actual and ideal robot positions by identifying the

geometric parameters of a robot.

The differential evolution algorithm proved to be

very effective and robust in the case of a serial-parallel

hybrid robot, and the calibration was giving good re-

sults on the simulation of 15 measurements and all of

the 54 geometrical error parameters were successfully

identiﬁed. The precision of the ﬁnal optimization

function approached the scale of 10

−22

(Wang et al.,

2012). Even with a smaller number of measurements,

the different genetic algorithms were able to com-

Turkovi

c, M., Švaco, M. and Jerbi

c, B.

Intelligent Algorithms for Non-parametric Robot Calibration.

DOI: 10.5220/0010176900510058

In Proceedings of the International Conference on Robotics, Computer Vision and Intelligent Systems (ROBOVIS 2020), pages 51-58

ISBN: 978-989-758-479-4

pensate for as much as 87% of the positioning error.

The number of measured points was 12, and the per-

formance of the four different algorithms was com-

pared (Barati et al., 2011). Improved quantum par-

ticle swarm optimization (IQPSO) also proved as an

effective algorithm for the identiﬁcation of the robot

parameters (Wang et al., 2016). The mean squared

error (MSE) of 260 positions measured by the laser

tracker was 2.80 mm, and after IQPSO optimization,

the MSE was only 0.07 mm. Compared with the or-

dinary particle swarm optimization algorithm (Alici

et al., 2006), the convergence speed was improved by

200%. The genetic algorithm can also be used to es-

tablish and identify the whole geometric model of a

robot (Dolinsky et al., 2007). The mapping between

the ideal and the realized robot positions were based

on a dataset of 30 robot measurements. Another 30

positions were used for the validation of the calibra-

tion and the MSE was improved from 1.85 mm prior

to calibration to 0.77 mm after calibration.

Parametric calibration has fast convergence, the

computation cost is low and the insight into the error

sources is provided. Geometrical errors are usually

the main cause of robot inaccuracy and they are re-

sponsible for up to 90% of the total positioning errors

(Judd and Knasinski, 1990). However, non-geometric

error sources (such as joint compliance errors caused

by the robot weight and the payload, link deﬂection

errors, backlash in gear transmission and thermal ef-

fects) make a smaller but still a signiﬁcant contribu-

tion to the positional error of the robot (Elatta et al.,

2004). It is difﬁcult to model these effects paramet-

rically because their number is too great to consider

every one of them, but they can be corrected with

non-parametric calibration. This type of calibration is

independent of the robot model, and one of the meth-

ods used for non-parametric calibration is optimiza-

tion with neural networks. It consists of three basic

steps: measurement and the recording of the real and

expected position of the robot, training and testing

the neural network which simulates the behaviour of

the robot and using the neural network output for the

compensation of the error.

Neural networks were mostly used as an addi-

tional step in the calibration process for compensation

of the non-geometric errors after the kinematic pa-

rameters have been determined (Aoyagi et al., 2010).

The ﬁrst experiments in using neural networks for

robot calibration started three decades ago, and the

artiﬁcial neural network managed to reduce the ab-

solute positioning error by 1/3 for a 6-DOF manip-

ulator (Takanashi, 1990). This was succeeded with

a small dataset of 25 measured points. A Recur-

rent Neural Network (RNN) was also used for both

the simulated and the experimental calibration of a 6-

DOF robot (Xiao-Lin Zhong and Lewis, 1995). Only

the internal joint measurements were used while the

manipulator was in contact with the constraint plane,

which generated the identiﬁcation equations. A Hop-

ﬁeld type RNN was used for solving these equations

and kinematic parameters were extracted. In total,

120 points have been used and position accuracy has

been improved to the level of robot repeatability. A

back-propagating neural network was used to com-

pensate the joint transmitting error, but only after the

geometric calibration of the robot (Liu et al., 2007).

The input values for the neural network were joint

angles and the information about the rotation direc-

tion, and the output was the angle by which the mo-

tors should rotate. The number of measured points

was 19, and the robot workspace size was 15 x 15 x

15 cm. Experimental veriﬁcation showed the MSE

decreased from 3.7 mm prior, to 0.5 mm after the cal-

ibration process. More extensive data was provided

with automated measuring system, which collected

more than 10.000 robot positions and conﬁgurations

(Zhao et al., 2019). The two-step calibration process

consisted of a parametric calibration which identiﬁed

the geometric parameters, and a non-parametric cali-

bration which identiﬁed the nonlinear residual errors

by using deep neural networks. The MSE was re-

duced from 1.81 mm to 0.10 mm. The repeatability

accuracy of the robot was 0.05 mm. Other compensa-

tions of non-parametric effects were made with neu-

ral networks after identiﬁcation of a robots geometric

parameters by using the extended Kalman ﬁlter algo-

rithm (Nguyen et al., 2015) and joint angle division

(Wang et al., 2019). Experimental validations of both

methods conﬁrmed the enhanced position accuracy,

which was increased from 3.59 mm to 0.42 mm in the

ﬁrst, and from 17 cm to 4.5 cm in the second example.

Shallow neural networks were used on a simu-

lated dataset, which demonstrated the superior perfor-

mance of a non-parametric calibration with a neural

network in comparison with bilinear and fuzzy inter-

polations (Bai and Wang, 2019). The absolute posi-

tion accuracy of a drilling robot was also improved

by using the algorithm based on the extreme learning

machine (Yuan et al., 2018). The input of the neural

network was ideal position of a robot and the output

was positional error measured by a laser tracker. The

robot controller was directed to compensate for the

predicted positional errors. By using this method, the

absolute position was improved by 75.89%. It was

also shown that choosing different hyperparameters

of a neural network could increase the accuracy.

The main advantage of the non-parametric cali-

bration lies in the possibility of simple application to

ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems

many different geometries of a robot, which could po-

tentially lower the cost and time needed for the cali-

bration of tailor-made and unique robots. Since the

geometric model does not have to be taken into con-

sideration, calibration is not limited to a pre-deﬁned

model of a robot. The biggest drawback of this ap-

proach is the neural networks tendency to be data-

hungry and the need for a large amount of measure-

ments. Furthermore, there are many network hyper-

parameters which can be adjusted, and this can gen-

erate unwanted errors if the hyperparameters are not

tuned appropriately for the given optimization prob-

lem.

In this paper, we propose a novel method of an

intelligent algorithm which could further improve the

process of calibration by searching for the best hyper-

parameters of a back-propagating feed-forward neural

network.

2 METHODS

Neural networks are universal approximators for non-

linear functions and their behaviour is loosely mod-

eled in resemblance to the interconnected neurons in a

biological brain, which transmit and process the data.

The problems are usually formulated in a way so that

the loss function (the measure of a discrepancy be-

tween the solution predicted by the network and the

solution which is expected and given by the train-

ing set) is minimized on a training dataset, by using

an optimization function which provides the means

for minimization, for a set number of epochs. The

reason for good performance on the various types of

problems is the usage of different activation functions

which introduce nonlinearities in the algorithm. The

challenge which arises from using neural networks

for the robot calibration is the amount of data needed

for successful optimization. Usually, not many mea-

surements for the calibration process are obtained,

because such measurements are time-consuming and

expensive. This can be partially compensated by

choosing a network architecture and hyperparameters

suitable for the speciﬁc problem.

While the non-parametric approach with neural

networks is overshadowed by their usage as an addi-

tional step in parametric calibration, there is little re-

search in their direct applications in the process of cal-

ibration. The objective of this experiment was to show

if neural networks can behave in the same way as the

robot that needs to be calibrated, simulating the ex-

act same errors in the robots resulting orientation and

position. However, no insights can be gained about

the error sources as in a parametric calibration; with

Figure 1: Measurement of the robot positions with a laser

tracker.

its hundreds or thousands parameters neural networks

virtually behave equivalent to a black box because of

the sheer complexity of the code. Unlike the paramet-

ric calibration, this process does not require both the

robot model and the measurements. Instead, only the

measurements should be provided.

The positions of the 6-DOF KUKA KR6 R900

robot were measured with a high-accuracy FARO

ION laser tracker (Figure 1), with the mean per-

centage error of 0.018 mm. The theoretical loca-

tions which the robot was commanded to reach were

recorded as information about the idealized positions

), in opposition to measured positions of the robot

), and the difference in those two values equals the

robot positioning error. A total of 366 robot positions

were measured. The data was divided into two groups

- the group of idealized positions of the robot (P

)

was used as the input for the neural network, and the

group of associated measured positions of the robot

) was used as the output for the neural network.

The dataset was then divided into two sets - the train-

ing set with 315 input/output pairs (P

, P

) and the

test set with 51 input/output pairs (P

, P

). Every po-

sition P consisted of six values, three of which denote

spatial coordinates (x, y, z) and the other three which

denote the orientation (r, p, y) of the robot.

The neural network used was a feed-forward,

back-propagating network, with two hidden layers

and interconnected neurons in each layer (the number

of neurons was 50). Linear and hyperbolic tangent

functions were used as activation functions, mean ab-

solute error was used for the loss function and the

Adam optimization (Kingma and Ba, 2014) for mini-

mizing the loss function. The learning rate was adap-

tive - the staircase exponential decay was used, and

the input and output pairs were normalized.

Intelligent Algorithms for Non-parametric Robot Calibration

Figure 2: Displacement of the robot manipulator for the

KUKA KR6 R900 before and after optimization.

The distribution of the difference between the

measured (P

) and idealized positions (P

) for (x, y, z)

components before optimization and the distribution

of the difference between the expected and calculated

positions after the optimization with neural network

was calculated (Figure 2). Although the distribution

of the error after optimization got smaller by an or-

der of magnitude, the error was still quite large. The

reason for such underperformance could perhaps be

found in an inadequate choice of network hyperpa-

rameters.

For the validation of that assumption, the perfor-

mance of the same neural network was then analyzed

on various robot simulations, which were specially

constructed to introduce datasets of robots with var-

ious complexity. The input/output pairs (P

, P

) were

generated for:

• a planar linear robot with N translational links

• a planar articulated robot with N rotational joints

Figure 3: Schematic representation of the linear (a) and ar-

ticulated (b) planar robots in special case with two links.

The planar linear robot with N links (Figure 3a)

was generated by stacking new links perpendicularly

to the formerly added link. The idealized position (P

)

was a set of random x and y positions, while the real-

ized position (P

) had an additional constant error (δx

and δy) for every link.

The data for the planar articulated robot with N

links (Figure 3b) was generated by choosing a ran-

dom set of N joint angles (θ

, θ

, ..., θ

) and using the

following equation for the idealized positions P

(x, y):

x =

∑

i=1

cos(

∑

j=1

), y =

∑

i=1

sin(

∑

j=1

) (1)

The l

represents the link length for the ith joint.

For the calculation of the realized robot positions

error

, y

error

), errors in the link lengths (δl) as well

as errors in the joint angles (δθ) were introduced:

error

∑

i=1

+ δl

)cos(

∑

j=1

(θ

+ δθ

)) (2)

error

∑

i=1

+ δl

)sin(

∑

j=1

(θ

+ δθ

)) (3)

With these equations for the linear and articu-

lated planar robots, it was possible to quickly gen-

erate the ”ideal” and ”measured” datasets and to

examine the performance of a former neural net-

work previously used for an optimization of a KUKA

KR6 R900 dataset. The performance of the network

was deﬁned as the mean squared error of the dif-

ference in P

error

, y

error

) given by the dataset and

error

, y

error

) predicted by the neural network. The

results were satisfactory in the case with one link for

both robots, but in contrast to the linear robot which

showed good performance (although very slowly de-

creasing as the new links were added), the perfor-

mance of the neural network for the articulated robot

with more than two links signiﬁcantly decreased by

two orders of magnitude (Figure 4). From this result it

was possible to conclude that the choice of the neural

network hyperparameters used on the speciﬁc prob-

lem of the 6-DOF articulated robot was inadequate.

Figure 4: Comparison of the MSE of the linear and the ar-

ticulated robot after optimization.

One of the most challenging tasks will be to de-

termine the best architecture and hyperparameters of

ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems

the neural network for solving the speciﬁc calibra-

tion problem when non-linearities are introduced. For

the calibration attempt of the 6-DOF KUKA KR6

R900 robot, another computer-generated model was

created, based on the aforementioned robot.

The robot position is calculated by forward kine-

matics, for which the Denavit-Hartenberg parameters

of the robot (θ, α, d, a) are used. Here, θ stands for the

joint angle of the robot, while α, d and a are inherent

constants which describe the geometry of the robot

and deﬁne the robot’s kinematic chain. The model

is also taking into account 24 different kinematic er-

ror parameters (δθ, δα, δd and δa). At the beginning

and the end of the kinematic chain, the robot base ref-

erence frame as well as robot ﬂange reference frame

were added. The position of the robot is calculated by

multiplication of matrix transformations (Jerbi

c et al.,

2020):

T = T

base

f lange

(4)

Each transformation for the modiﬁed Denavit-

Hartenberg notation equals:







cθ

−sθ

0 a

sθ

cα

cθ

cα

sα

sθ

sα

cθ

sα

cα

0 0 0 1







, i = 1, ..., 6

(5)

The abbreviations for the sine and cosine func-

tions were used (c = cos and s = sin). The coordinates

and orientations in (P

, P

) dataset can be calculated

from T .

To ﬁnd the best hyperparameters of the neural net-

work, the genetic algorithm, which is searching for

the best solution from the population of all potential

solutions, was constructed. At the beginning, a ran-

dom population of the individuals was created. In ev-

ery new generation, the selected individuals are the

best performing ones, and the new possible solutions

were added to the population by recombinations and

mutations of the best-performing individuals. Since

the population is generated completely at random, ge-

netic algorithms have slow convergence speed.

The pseudocode is given as follows:

1: t = 0

2: Population initialization P(t)

3: Evaluation of the population P(t)

4: while (t < T):

5: t = t + 1

6: P’(t) = Selection of the P(t-1)

7: P’’(t) = Mutation of the P’(t)

8: P’’’(t) = Recombination of the P’’(t)

9: Evaluation of the new population P’’’(t)

10: P(t) = P’’’(t)

In this paper we consider the novel method for

robot calibration by using the neural networks care-

fully selected by the genetic algorithm and investigate

its potential in the future usage.

3 RESULTS

The same genetic algorithm was used for both the

parametric and the non-parametric optimization, but

the population for each problem was generated in a

different way. The individual solutions for the para-

metric optimization represented the correction of the

DH parameters used for the calculation of the for-

ward kinematics. Every individual of the population

consisted of 24 numbers in the range of [10

−8

, 10

−2

and the data was distributed evenly across the whole

range. The input and output pairs were formed

by computer-generated datasets for the KUKA KR6

R900, and the data was generated for three datasets

with 10, 100 and 1000 pairs of ideal and associated

realized locations of the robot. Best-performing indi-

viduals were selected and added to the new population

by means of crossovers and mutation. A signiﬁcant

improvement in the accuracy was obtained (Figure 5),

which conﬁrmed the validity of the usage of genetic

algorithms in the parameter identiﬁcation problems.

Although there were no new insights in using the ge-

netic algorithms in robot calibration, the reference for

the best obtained accuracy was provided, as well as

the time needed for the optimization (Table 1).

Although the number of the individuals in the pop-

ulation was relatively low (30 in each new gener-

ation), all of the three different datasets eventually

reached the satisfactory accuracy. As expected, the

convergence was faster for the largest dataset. Con-

sidering the computation time, a signiﬁcantly less

time was needed for the dataset with 100 points. The

trade-off for a small increase in precision, as in the op-

timization of the biggest dataset with 1000 robot po-

sitions, means the computation time might be several

times longer. However, with different randomly gen-

erated initial population, the convergence speed could

be a lot faster or slower.

The MSE after optimization was tested on a com-

pletely new dataset speciﬁcally created for measuring

the performance of the algorithm, which is the rea-

son the error does not necessarily decrease in time.

Since the generation number varies for every dataset,

for comparison were depicted only the ﬁrst 1641 gen-

erations (Figure 5), although the datasets with 10 and

100 points also eventually reached the satisfactory ac-

curacy (Table 1).

The non-parametric optimization had a different

Intelligent Algorithms for Non-parametric Robot Calibration

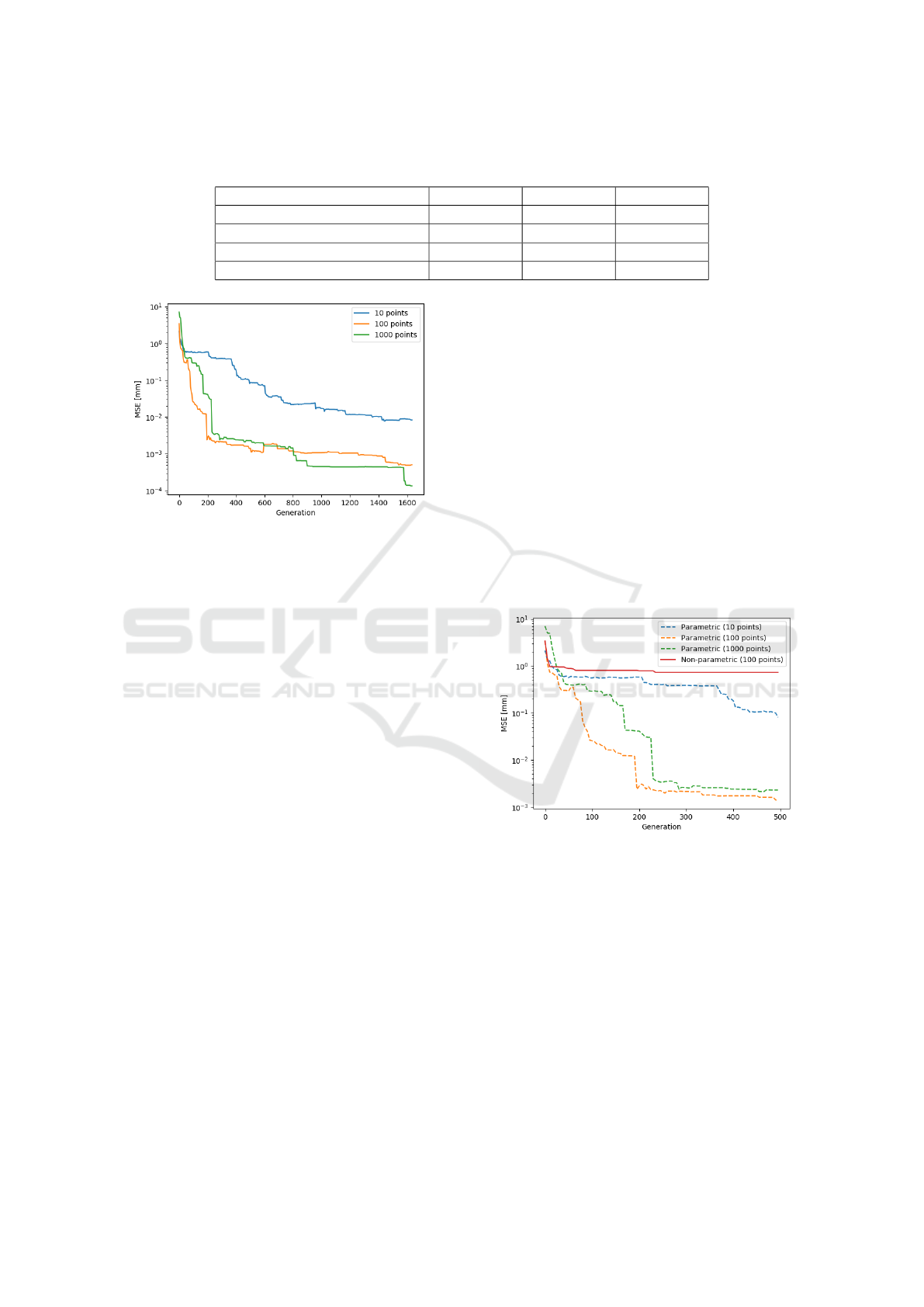
Table 1: The comparison of the mean squared errors after optimization with respect to number of generations and optimization

time for various datasets.

Dataset size 1000 100 10

MSE before optimization [mm] 7.92 8.96 14.26

MSE after optimization [mm] 1.34 × 10

−4

2.04 × 10

−4

5.06 × 10

−4

Number of generations 1641 4451 99996

Optimization time [min] 490 134 366

Figure 5: The behaviour of the mean squared errors for the

parametric optimization by using the genetic algorithm for

three different-sized datasets.

set of initialized population, whose individuals con-

sisted of a variable number of layers, a random num-

ber of neurons for each layer, randomly chosen activa-

tion functions, optimization functions and loss func-

tions. The batch number was also set to random as

well as the normalization range. Sometimes the abil-

ity of the algorithm to generalize well worsens with

time and longer training time does not always guar-

antee better results. For that reason, the number of

epochs of the neural network was also random.

The performance of the different neural net-

work architectures with different hyperparameters

was tested, and the genetic algorithm once again se-

lected the best-performing individuals and added new

population of similar solutions by using crossovers

and mutations. This process seemed very promising

considering the success of both the genetic algorithms

and neural networks in robot calibration. However,

because of the duration of the optimization process,

no new improvement was accomplished (Figure 6).

Time needed for reaching the 500th generation was

166 minutes. This would not be considered long given

the signiﬁcant improvement in accuracy. But in com-

parison to parametric calibration, the search for the

best neural network architecture was underperform-

ing. The mean squared error for the best-ranked neu-

ral network after 500 epochs was 0.73 mm, and for

the best-ranked parametric calibration for the 10, 100

and 1000 points were 5.06 × 10

−4

mm, 2.04 × 10

−4

mm and 1.34 × 10

−4

mm, respectively.

The reason for this might be found in the be-

haviour of the loss function in the parametric space.

It was generally believed that neural network should

search for global optima and the local optima solu-

tions were not seemed as important. However, the

new research is starting to show that the parametric

space is very densely populated by a large number

of local minima which give results almost as good

as those of the global minimum (Kawaguchi et al.,

2019). No matter what parameters we choose, there

is a great probability the neural network’s solution

found in the local minima will be good enough for

practical applications. In this light, the usage of the

genetic algorithm for choosing the right neural net-

work architecture is not the best way the robot cali-

bration could be done.

Figure 6: The comparison of the MSE for the parametric

and non-parametric optimization.

Since the attempt at the optimization did not

reach the expected values (Figure 2), and no new in-

sights into the architecture of the neural network were

gained, the validity of the usage of neural networks

for optimization in robot calibration was questioned.

The generated input and output pairs (P

, P

) for the

KUKA KR6 R900 robot were used for veriﬁcation of

the universal approximation theorem, which claims

that the neural networks should be able to approxi-

mate arbitrary and continuous non-linear functions to

any desired accuracy (Kidger and Lyons, 2019). To

verify this theory, the random neural network archi-

tecture was generated, as well as the data in certain

ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems

volume range. For the ﬁrst dataset, the points were

generated in the 2m

volume. For the second dataset,

the points were generated in the 2dm

volume, and

for the third dataset in the 2cm

volume. The various

dataset sizes were used.

The randomly chosen parameters of the neural

network were generated, and the theorem was con-

ﬁrmed - the neural network reached the desired accu-

racy for the dataset in the small volume because of the

largest density of the data (Figure 7). With more data,

the optimization process would perform even better.

However, for the purpose of the non-theoretical robot

calibration, the number of measured points should be

below four-digit number.

Figure 7: The behaviour of the MSE with respect to the size

of the input and output datasets, for different volumes.

4 DISCUSSION AND

CONSLUSION

Since the non-parametric robot calibration by using

neural networks was sparsely researched, the possi-

bility of calibration was immediately tested on the

KUKA KR6 R900 robot. The usage of the neural net-

works in the calibration problems showed unsatisfac-

tory results in simulating the behaviour of a 6-DOF ar-

ticulated robot. For that reason, computer-simulated

datasets for two planar robots with different complex-

ities were generated. For the linear robot the cali-

bration proved possible, as opposed to the articulated

robot for which the optimization proved impossible as

soon as additional complexity was introduced.

There are many hyperparameters of the neural net-

work which can be tuned. Otherwise the network

does not produce good approximations for the given

optimization problem. In this paper, a novel method

which uses the genetic algorithms to ﬁnd an appro-

priate network architecture was proposed, since the

choice of appropriate hyperparameters is of extreme

importance.

Besides the non-parametric, a parametric-

optimization method was tested for reference. The

genetic algorithm was also used, but in this case, the

population consisted of the geometric parameters

which were needed to be identiﬁed. The comparison

of the non-parametric and the parametric optimiza-

tion was made on a simulated dataset, and the faster

convergence and better performance of the parametric

optimization was demonstrated.

The validity of the non-parametric calibration at-

tempt was also questioned and tested with massive

datasets. For massive datasets, the feed-forward back-

propagating neural network proved as a good opti-

mizer. However, for the simulation of the complex

robot behaviour, more speciﬁc types of network struc-

tures should be researched. Preferably, the number of

the measured positions should be as small as possible

to speed up both the measuring and the calibration

process, but large enough for the model to be able

to generalize well on the whole working space of the

robot.

The solutions considered in this paper are time-

invariant, which does not hold true for the real robot.

Because of the possibility for some manipulators to

reach certain points by alternative joint conﬁgura-

tions, the positional errors will be different. It should

prove valuable to consider, in the future research, how

the former movement of the robot affects the error and

if it is possible to make a correction with the neu-

ral networks. By using recurrent networks such as

the LSTM (Long Short-Term Memory), which pro-

cess entire sequences of data, it might be possible to

address this issue. The use of Bayesian Neural Net-

works might also produce better approximations on

smaller datasets because they could extract more in-

formation than other neural networks.

REFERENCES

Alici, G., Jagielski, R., Sekercioglu, A., and Shirinzadeh,

B. (2006). Prediction of geometric errors of robot ma-

nipulators with particle swarm optimisation method.

Robotics and Autonomous Systems, 54:956–966.

Aoyagi, S., Kohama, A., Nakata, Y., Hayano, Y., and

Suzuki, M. (2010). Improvement of robot accuracy

by calibrating kinematic model using a laser tracking

system-compensation of non-geometric errors using

neural networks and selection of optimal measuring

points using genetic algorithm. In 2010 IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems, pages 5660–5665.

Bai, Y. and Wang, D. (2019). Using Shallow Neural Net-

work Fitting Technique to Improve Calibration Accu-

racy of Modeless Robots, pages 623–631.

Intelligent Algorithms for Non-parametric Robot Calibration

Barati, M., Khoogar, A., and Nasirian, M. (2011). Esti-

mation and calibration of robot link parameters with

intelligent techniques. Iranian Journal of Electrical

and Electronic Engineering, 7:225–234.

Dolinsky, J., Jenkinson, I., and Colquhoun, G. (2007). Ap-

plication of genetic programming to the calibration of

industrial robots. Computers in Industry, 58:255–264.

Elatta, A., Gen, L., Zhi, F., Daoyuan, Y., and Fei, L. (2004).

An overview of robot calibration. Information Tech-

nology Journal, 3:74–78.

Gang, C., Tong, L., Ming, C., Xuan, J. Q., and Xu, S. H.

(2014). Review on kinematics calibration technology

of serial robots. International Journal of Precision

Engineering and Manufacturing, 15:1759–1774.

Jerbi

c, B.,

Svaco, M., Chudy, D.,

Sekoranja, B.,

Suligoj,

F., Vidakovi

c, J., Dlaka, D., Vitez, N.,

Zupan

c, I.,

Drobilo, L., Turkovi

c, M.,

Zgalji

c, A., Kajtazi, M.,

and Stiperski, I. (2020). RONNA G4 — Robotic neu-

ronavigation: A novel robotic navigation device for

stereotactic neurosurgery. In Handbook of Robotic

and Image-Guided Surgery, pages 599 – 625. Elsevier.

Judd, R. P. and Knasinski, A. B. (1990). A technique to

calibrate industrial robots with experimental veriﬁca-

tion. IEEE Transactions on Robotics and Automation,

6(1):20–30.

Kawaguchi, K., Huang, J., and Kaelbling, L. (2019). Every

local minimum value is the global minimum value of

induced model in nonconvex machine learning. Neu-

ral Computation, 31:1–31.

Kidger, P. and Lyons, T. (2019). Universal approximation

with deep narrow networks.

Kingma, D. and Ba, J. (2014). Adam: A method for

stochastic optimization. International Conference on

Learning Representations.

Liu, J., Zhang, Y., and Li, Z. (2007). Improving the po-

sitioning accuracy of a neurosurgical robot system.

Mechatronics, IEEE/ASME Transactions on, 12:527

– 533.

Nguyen, H.-N., Zhou, J., and Kang, H.-J. (2015). A cali-

bration method for enhancing robot accuracy through

integration of an extended Kalman ﬁlter algorithm

and an artiﬁcial neural network. Neurocomputing,

151:996–1005.

Takanashi, N. (1990). 6 DOF manipulators absolute

positioning accuracy improvement using a neural-

network. In EEE International Workshop on Intelli-

gent Robots and Systems, Towards a New Frontier of

Applications, pages 635–640 vol.2.

Svaco, M.,

Sekoranja, B.,

Suligoj, F., and Jerbi

c, B. (2014).

Calibration of an industrial robot using a stereo vision

system. volume 69, page 459–463.

Wang, F., Wang, Y., Li, J., and Fang, W. (2016). Kinemat-

ics Parameters Identiﬁcation for IRB 1400 Using Im-

proved Quantum Behaved Particle Swarm Optimiza-

tion, volume 386, pages 881–890.

Wang, Y., Wu, H., and Handroos, H. (2012). Error

modelling and differential-evolution-based parameter

identiﬁcation method for redundant hybrid robot. In-

ternational Journal of Modelling and Simulation, 32.

Wang, Z., Chen, Z., Wang, Y., Mao, C., and Hang, Q.

(2019). A robot calibration method based on joint an-

gle division and an artiﬁcial neural network. Mathe-

matical Problems in Engineering, 2019:1–12.

Xiao-Lin Zhong and Lewis, J. M. (1995). A new method

for autonomous robot calibration. In Proceedings of

1995 IEEE International Conference on Robotics and

Automation, volume 2, pages 1790–1795 vol.2.

Yuan, P., Chen, D., Wang, T., Cao, S., Cai, Y., and Xue,

L. (2018). A compensation method based on extreme

learning machine to enhance absolute position accu-

racy for aviation drilling robot. Advances in Mechan-

ical Engineering, 10:168781401876341.

Zhao, G., Zhang, P., Ma, G., and Xiao, W. (2019).

System identiﬁcation of the nonlinear residual er-

rors of an industrial robot using massive measure-

ments. Robotics and Computer-Integrated Manufac-

turing, 59:104–114.

ROBOVIS 2020 - International Conference on Robotics, Computer Vision and Intelligent Systems