
Multi Input Single Output Fuzzy Model to Evaluate the Performance
of Distance Education Media
Wassan Adnan Hashim
1 a
, Faiz A. Mohammed Alawy
2
and Jawad Hamad Hameed
3
1
Information Technology Department, Qala University College, Erbil, Iraq
2
Promoting Sustainable Change Inc, Michigan, U.S.A
3
Department of Petroleum Systems Control Engineering, Tikrit University, SalahAldin, Iraq
Keywords: Distance Education, Media, Adaptive Neuro-Fuzzy Inference System, MATLAB.
Abstract: Distance learning is being the preferred mean for continuous learning at any educational center and there is
urgent need to adapt with the technological requirements for such open learning methods. A fuzzy logic
based model has been introduced in this work to estimate the overhaul efficiency of the distance education
media to meet specific training objective. This fuzzy model has been tested to simulate the Tony Bates
“ACTIONS” model (Bates, 1995). The performance of the model has been validated by comparing the
model results with actual examples which have been obtained by conducting practical survey. The fuzzy
ANFIS model has been trained using back-propagation and least-square methods.
a
https://orcid.org/0000-0001-8473-8595
1 INTRODUCTION
The impact of the rapid development in the fields of
telecommunication and digital technologies have
helped in delivering online and distant learning
which in turn has expanded the learning
opportunities; because of this rapid technology
development and the availability of different
educational tools, organizations are facing many
challenging decisions to enhance their educational
systems. Learning centres are working
seriously
to
meet the fast growing needs for continuous learning
by redefining their systems to be more attractive for
the new and old learners. Universities, schools, and
training centres are developing new contents and
medias to make it easy for any person to reach out to
the learning resources at any time, with minimum
cost and easy access throughout the world (Teixeira
and Bates, 2019; Kappel and Lehmann, 2002; Zhang
and Jiang).
There are very limited practical theories for
selecting the most suitable learning media for certain
systems and the most common practice is to have the
organization management or a special committee of
experts to decide the best technology tools for each
specific case. The ACTIONS model (Bates, 1995) is
the most famous model for selecting the optimal
learning media which was developed for campus-
based as well as distance education. More detailed
approaches are also available at more micro-level
when it comes to designing specific multimedia
educational materials (Holden and Westfall, 2007)
(Simonson and Zvacek, 2019).
A model for technology selection is very
important to help covering a wide variety of learning
contexts and suggests strategic and tactical
institutional and instructional plans on both of
educational and operational issues. The optimal
design of an educational model should accommodate
new technology development and create a cost
effective system. As an example, SECTIONS is
found to be one of the best models to provide the
required needs. SECTIONS stands for: Student,
Ease of use, Cost, Teaching function, Interaction,
Organizational issues, Networking, and Security &
privacy.
This work is introducing a new model which is
based on multi input signals; easiness to access the
teaching or learning, estimated costs, user-
friendliness & interactivity, organizational issues,
novelty, and speed of the required change. The
suggested model is designed by using Adaptive
Neuro-Fuzzy Inference System (ANFIS) method of
fuzzy based modelling.
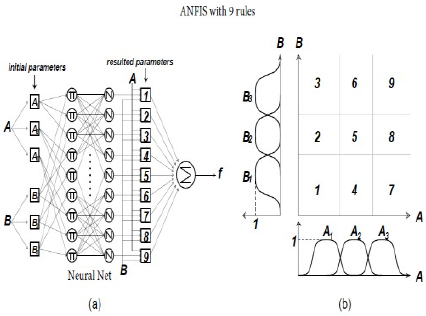
2 ANFIS MODEL DEFINITION
Modelling any specific system by using
conventional mathematical tools can be a very
difficult process especially when dealing with ill-
defined or uncertain systems, a process of several
pages of decision-trees, which are completely
impractical to apply. While a fuzzy inference system
employing fuzzy if then rules is much easier to
human knowledge and reasoning processes without
employing precise quantitative analyses. This fuzzy
modeling is first explored by Takagi and Sugeno
(Mehran, 2008; Yulianto and Komariyah, 2017).
Generally, there is no standard method to transform
the human experience into the rule base of a fuzzy
inference system in addition to the need to design a
tuning method to define the membership functions in
order to optimize the criteria of the output error and
performance index
ANFIS is an adaptive network based fuzzy
inference system which can be used as a basis for
constructing a set of fuzzy if-then rules with
appropriate membership functions to state the
required initial input-output pairs.
The basics of fuzzy if-then rules, fuzzy inference
systems, the structures and learning rules of adaptive
networks are described in (Al-Hmouz and Shen,
2011). In using ANFIS, there are almost no
constraints on the network structure and node
functions, but the network should be of feed forward
type (Salleh and Talpur, 2017). Figure 1 below
shows a simple example of a two input – nine rules
ANFIS system structure. A more complicated
structure of six input ANFIS model is used in this
work to model the distance education media
selection system.
Figure 1: Simple example of ANFIS structure with two
input – nine rules ANFIS.
3 DISTANCE EDUCATION
MODEL
The objective of designed ANFIS model is to
evaluate and enhance the media selection process
and to avoid the associated problems facing the
universities or education centers. Also, this ANFIS
model is introduced to estimate the overhaul
efficiency of the appropriate media for any
suggested distance education system using the
designing the parameters of Bates model.
3.1 Model Structure
Numerical and statistical data-based methods can be
complemented by the human expertise and
knowledge to design the required set of fuzzy rules
for a certain system. The modeling of distance
education media selection is designed using ANFIS
modeling techniques with six input parameters and
single output parameter. The Adaptive Neuro-Fuzzy
inference system (ANFIS) is a hybrid technique
which is based on fuzzy and neural networks to
enhance the performance of the system accuracy for
modeling and simulating complex systems with
none linear characteristics (Ritika and Bhardwaj,
2020). The required membership function
parameters for the designed fuzzy inference system
are calculated by feeding the given information that
is embedded in relation among the
input/output
training data sets. The ANFIS embedded learning
capabilities makes it more efficient and works
similarly to neural networks. The membership
functions parameters are tuned by using a
combination of back propagation and least squares
error minimization learning technique. Throughout
the learning process, the suggested membership
functions will continue to evolve until reaching the
required target error value. The calculation of fuzzy
membership functions is interpolated by gradient
vector to provide a measure of how well the
implemented fuzzy inference system is capable of
modeling the input/output data for a given set of
variables. The optimization process is applied to
adjust the network weights and parameters to
continuously reduce a previously designed output
error measure. This system is based on Sugeno-type
system to simulate the required model and analyze
the mapping relation between the input and output
data values and to determine the optimal distribution
of membership function (Qun, 2015). It is mainly
based on the fuzzy “if-then” rules from the Takagi
and Sugeno type. The equivalent Takagi and Sugeno
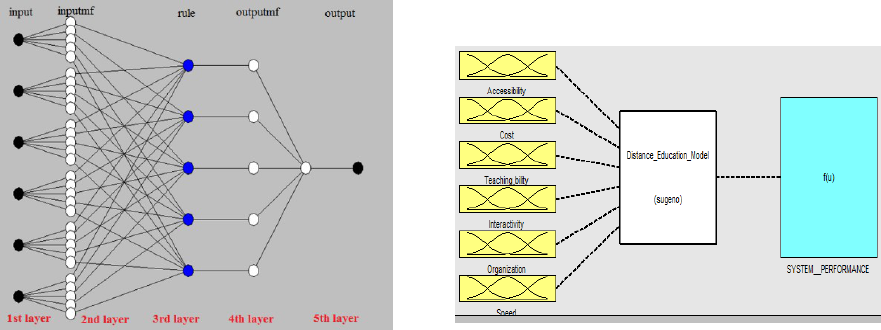
ANFIS architecture is shown in Figure 2. It contains
five successive layers and each layer involves
several nodes, with different node function per layer.
Figure 2: The equivalent Takagi and Sugeno ANFIS
Architecture.
The output signals from each node in the
previous layer is fed to the input signals in the
present layer. Each node is firing its output value
depending on its embedded activation function and
accumulated input from the previous layer. The node
output will be fed to the nodes in the next layer.
The below bullet points describe the
designed
ANFIS model:
Total number of network nodes: 30 + 5 + 1
Total number of the network linear parameters:
932
Total number of the network nonlinear
parameters: 28
Total number of the model parameters: 6 inputs
+ 1 output
The total number of the training data pairs: 500
The total number of used fuzzy rules: 19
Any text or material outside the aforementioned
margins will not be printed.
3.2 Model Input/Output Parameters
The fuzzy logic part of the ANFIS based model is
initially determined by the fuzzy sets of input/output
values which represent the possible values of these
variables. Figure 3 shows the general three stages of
the suggested model to simulate the distance
learning media selection system. Figure 3 shows a
sequence of six inputs to generate target single
output as a measure of the selected distance learning
media performance. That means, it is a multi-input
single output ANFIS model with six input
parameters (accessibility, cost, teaching,
interactivity, organization, and speed) and one
output parameter to indicate the selected distance
learning system performance.
Figure 3: The schematic model of the distance learning
media selection.
For each suggested set on these six input parameters,
the resulted output value is considered as the
estimated goodness of the distance learning media
for this specific state of input.
3.3 Membership Function
The fuzzy theory is based on the overlapped
triangular membership logic with a predefined
suitable width and values. Each element accordingly
can belong to a particular set with partial
membership value to each set. Depending on the
addressed problem, it is possible to define a suitable
membership function with certain environment and
limitation for each of the required variables. Table 1
below shows the initial description of the fuzzy sets
for a system with six input variables and the related
fuzzy classification
3.4 Fuzzy Rules Characteristics
Each of the six inputs of the designed system is
assigned to different levels of linguistic variables.
These variables have been tuned to generate only
nineteen rules. Keeping in mind that there are many
rules might be classified as 'not applicable'
conditions and accordingly are not included in the
designed set of accepted rules.
This ANFIS model for Bate’s ACTIONS
parameters is designed and trained by using
MATLAB fuzzy toolbox. The membership functions
are generated by using clustering algorithm.
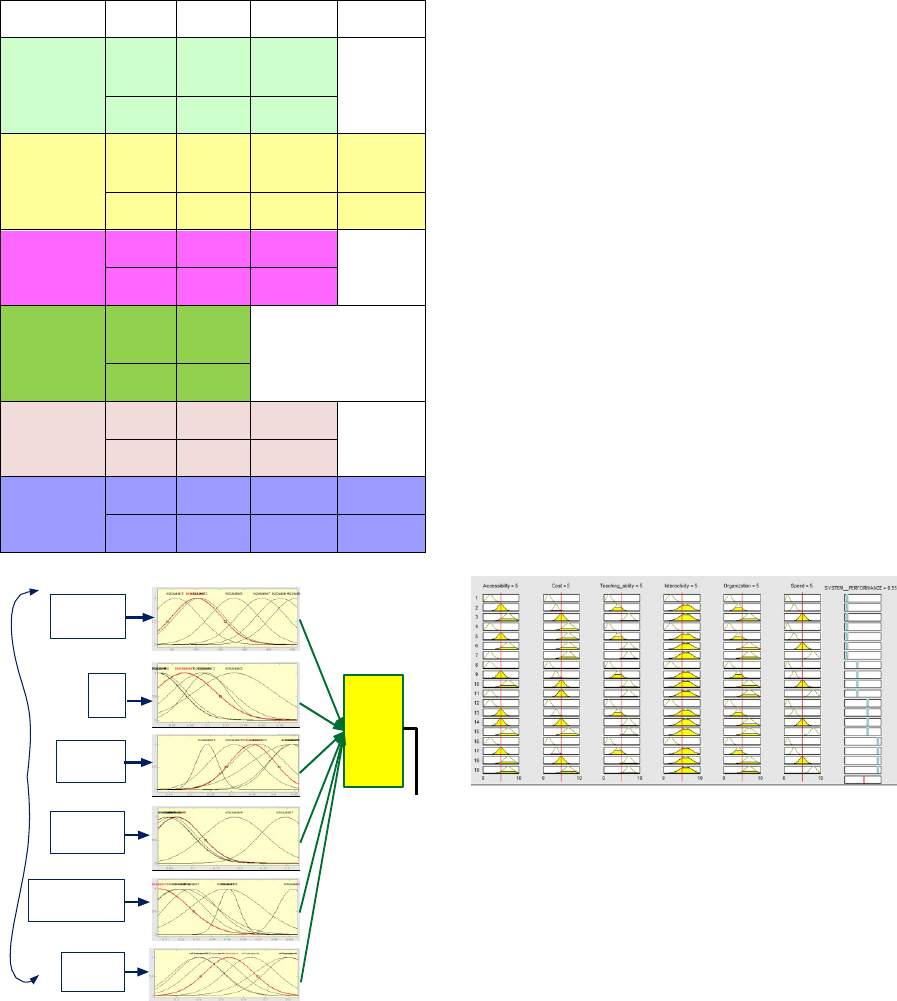
Table 1: The definition of the fuzzy input variables.
Input Cat.1 Cat.2 Cat.3 Cat.4
Accessibility
V.
Simple
Simple Difficult
0-4 3-7 5-10
Cost
V. Cheap Cheap Expensive
V.
Expensive
0-3 2.5-5 3-6 6-10
Teaching
ability
Bad Good V. Good
0-3 2-6 5-10
Interactivity
Not user
friendly
User
friendly
0-4 4-10
Organization
Bad Suitable V. Suitable
0-3 2.6-6 5-10
Speed
V. Slow Slow Fast V. Fast
0-2 1.8-4 3.5-6.7 6-10
Figure 4: The membership functions after the
ANFIS
training.
The training parameters are: Influential radius (Rc)
is 0.5, Quash factor (η) is 1.5, Accept ratio (R
Accept
)
is
0.5, and the Reject ratio (R
Reject
) is 0.15. The
applicable rules formulated for the model and the
memberships are given in Figure 4 below. The core
of the proposed ANFIS system is designed by using
fuzzy linear model type Sugeno which converts a
fuzzy inference engine into an adaptive network that
learns the relationship between inputs. The designed
system is defined by the Bate’s model input
parameters (accessibility, cost, teaching ability,
interactivity, organization, speed) while the single
output is defined as the related performance of the
tested distance learning system (sp).
The six input/single output bate’s model is used
to improve the converge speed of the ANFIS hybrid
leaning algorithm. The available data set is
randomly partitioned into a training set and a
checking (testing) sets. The training sets are a
practical description of the desired input/output data
which is used during the training stage to train the
model by minimizing the target output error. While
the checking data sets are used for the testing phase
and to carry out the cross validation of the ANFIS
model.
The first-order (linear) ANFIS is trained using
the hybrid algorithm of the back-propagation and
least-square methods available through the
MATLAB toolbox. The rule viewer is used to
generate the below example of value-relations for a
certain state of training parameters shown in Figure
5.
Figure 5: ANFIS rules shown by rule viewer.
The designed rules along with membership function
are also shown in rule viewer of fuzzy model as
given in the above Figure 5. This Figure 5 clearly
shows the characteristic of the six input parameters
for a certain example to present their accumulated
effect on the output variable.
4 TRAINING RESULTS AND
DISCUSSIONS
The first phase of the system design is the
convergence to the final shape of the ANFIS model
to optimize the distance education media selection
system for certain set of input variables. Then,
SYSTEM
PERFORMANCE,
SP
Parameters
Of
BATE
S
MODEL
ANFIS
(sugeno)
Accessibility
Cost
Interactivity
Teaching
ability
Organization
Speed

verifying the accuracy of the model in the testing
phase to demonstrate the designed model
performance. Figure 6 below is partially showing the
cross-relations among the six input variables and the
related interdependency of the model output value
on each of these inputs. Eight interdependent
relations were selected
randomly
to show eight
examples of the output surface area changing in
response to the associated change in two of the input
variables as shown in figure 6. The Eight different
three- dimensional relations for the system
performance shown in this figure prove that each of
the six input variables is affecting the final value of
the model output in a different way depending on the
pre- learning phase and the weighted effect of this
input variable and its interdependent relations with
the other input variables
Figure 6: Input/output surface area interdependent
relations.
Figures (7a) and (7b) are showing the ANFIS model
training to simulate the performance of Bate’s
ACTIONS model which is carried out by using 600
epochs before converging to the minimum accepted
preset error value. Figure (7c), is showing the final
ANFIS model output performance (output accuracy)
during the validation or checking stage
Figure 7: (a) Decrease of error during training phase.
(b) Decrease of error during testing phase.
(c) ANFIS prediction versus checking data set.
In this model a total of 50 input/output data sets are
used as practical examples to verify the model
accuracy. It was found that only two input data sets
were out of range and couldn’t meet the expected
target output value and the output error has exceeded
five percent. The rest of the validation data sets have
shown individual error less than three percent. Thus,
the overall average error for the model is about five
percent which means that the simulated fuzzy model
is giving an overall of 95 percent accuracy. It can be
concluded that the designed ANFIS model is very
accurate and there is a very small error percentage
which is acceptable compared to the huge efforts
required to carry out the process by using the tedious
conventional methods which depend on using
human calculations under different conditions.
5 CONCLUSION
The feasibility of using ANFIS model technique was
demonstrated to simulate a simple adaptive system
to estimate the optimal choice of distance education
media. A
multi-input
single output adaptive Neuro-
Fuzzy model was developed and the designed model
was validated by using pre-calculated experimental
results for given conditions. The demonstration
results proved that the designed fuzzy model
accurate enough to be used by the educational
organization who are planning to upgrade to new
learning systems. It has been concluded that the
model is about 95 percentage accurate. A model
with such accuracy can be used by the practicing
educational system designers who would like to get
quick answers by using this optimized simple
intelligent tool. This work has emphasized the fact
that ANFIS modeling technique can be used as a
viable alternative to carry out analysis without
conducting actual experiments which might be very
expensive and time consuming process. The system
was found to be very flexible and easy to use.
Modeling using ANFIS techniques was proved to be
very cost effective and practical alternative to the
conventional methods.
REFERENCES
Teixeira, A. M., Bates, T., & Mota, J., 2019. What future
(s) for distance education universities? Towards an
open network-based approach. RIED: Revista
Iberoamericana de Educación a Distancia, 22(1),
107-236.,
Kappel, H. H., Lehmann, B., & Loeper, J.,
2002.
Distance education at conventional universities in
Germany. The International Review of Research in
Open and Distributed Learning, 2(2).
Zhang, W., Jiang, G., & Niu, J., 2002. Web-based
education at conventional universities in China: A case
study. The International Review of Research
in Open and Distributed Learning, 2(2).
Holden, J. T., & Westfall, P. J. L., 2007. An instructional
media selection guide for distance learning. Online
Submission.
Simonson, M., Zvacek, S. M., & Smaldino, S. (2019).
Teaching and Learning at a Distance: Foundations of
Distance Education 7th Edition. IAP.
Mehran, K., 2008.
Takagi-Sugeno
fuzzy modeling for
process control. Industrial Automation, Robotics and
Artificial Intelligence (EEE8005), 262. Bates, P. C.
(1995). Debugging heterogeneous distributed systems
using event-based models of behavior. ACM
Transactions on Computer Systems (TOCS), 13(1), 1-
31.
Yulianto, T., Komariyah, S., & Ulfaniyah, N.,
2017.
August). Application of fuzzy inference system by
Sugeno method on estimating of salt production. In
AIP Conference Proceedings (Vol. 1867, No. 1, p.
020039). AIP Publishing LLC.
Al-Hmouz, A., Shen, J., Al-Hmouz, R., & Yan,
J.,
2011.
Modeling and simulation of an adaptive neuro-fuzzy
inference system (ANFIS) for mobile learning. IEEE
Transactions on Learning Technologies, 5(3), 226-
237.
Salleh, M. N. M., Talpur, N., & Hussain, K.,
2017.
Adaptive neuro-fuzzy inference system: Overview,
strengths, limitations, and solutions. In International
Conference on Data Mining and Big Data (pp. 527-
535). Springer, Cham.
Ritika, Reenu Dhaiya, Rishabh Bhardwaj,
2020.
Hybrid
Technique for Data Scrutiny using Artificial
Intelligence, International Journal of Recent
Technology and Engineering (IJRTE) ISSN: 2277-
3878, Volume-8
Issue-5.
Qun Ren, 2015. Type-2 Takagi-Sugeno-Kang Fuzzy Logic
System and Uncertainty In Machining, Thèse
présentée en Vue De L’obtentiondu Diplôme De
Philosophiae Doctor(Génie Mécanique), Université De
Montréal.
