Impact of Internal Parameterization on the Performance of Support

Vector Machines for Crop Mapping Sentinel-2 NDVI Time Series

Badr-Eddine Sebbar

, Aicha Moumni

and Abderrahman Lahrouni

LMME, Centre Geber, Faculté des Sciences de Semlalia, UCA,

Marrakech, Morocco

Keywords: Support Vector Machines, Remote-sensing, classification, Kernel function, parameterization, performance

evaluation.

Abstract: The Support Vector Machines classifiers has been increasingly used to derive land-cover/ land-use

information from satellite imagery. As software implemented classifiers, SVM give satisfactory but imperfect

results, when performed at first using the default set of parameters. Thus, obtaining the best results requires a

basic understanding of the theory behind their workings and how their accuracy can be parametrically

influenced. In this paper, we report the result of an investigation of the SVM’s different parameters, applied

to satellite data for crop mapping, in order to develop some guides for parameterizing this classification

technique. The internal parameters considered in this study include the Kernel function, Pyramid Level,

Penalty parameter, Gamma parameter, the Bias and the Degree. A set of 21 NDVI time-series layer-stack,

extracted from Sentinel-2 (S2) images, were used. The results showed that the Kernel function choice, and

the four internal parameters, namely, Penalty parameter, Gamma parameter, the Bias and the Degree, can

improve the classification accuracy. The best overall accuracy reached 94.50% using the polynomial function.

1 INTRODUCTION

With the contribution of remote sensing latest high

spatio-temporal resolution imagery (HSTRI), land-

cover classification and crop mapping have become

essential tools in agricultural management by

regularly assessing the vegetation status using various

technics in different parts of the globe (Anderson,

Allen, Morse, et al 2012; Mulla, D. J. 2013;

McDowell, Nate G., et al. 2015; Lawley, V., et al.

2016; Khanal, S., et al 2017). Nowadays, the

available and free S2 data, is the most popular source

of HSTRI used by researchers and decision makers

for this purpose (Moumni, A., et al 2019; Moumni,

A., et al 2020). In addition to remote sensing data

qualities, classification algorithms play an important

role in improving performance accuracies of crop

maps. Many previous studies have been focusing on

comparing various, well-known classification

algorithms in the remote sensing community in order

to provide useful documents describing the methods

https://orcid.org/0000-0002-1276-6877

https://orcid.org/0000-0002-0203-8462

https://orcid.org/0000-0002-2118-8570

and procedures for image classification . Different

articles compared different sets of classification

algorithms, Yu, Le, et al., (2014) investigated the

relationship between the classification accuracy,

publication date, extent of the study area, and

accuracies for different sensors and classification

algorithms. Li, Congcong, et al., (2014) compared the

performances of 15 image classification algorithms,

with the same Landsat Thematic Mapper (TM) data

set and the same classification scheme over

Guangzhou City, China. In terms of algorithms

performances, most case studies give different

outcomes, despite extensive work on classification

methods, questions comparing different techniques

remain unanswered (Khatami, R., et al 2016), for

example, sometimes Neural Networks (NN) performs

slightly better than Support Vector Machine (SVM),

sometimes it’s the other way, which depends on the

size of data, how it is handled and more importantly

the parameters configuration of each algorithm,

suffering from assignment issues, they significantly

can sometimes give unsatisfactory results. In this

context, certain studies have been focusing on the

evaluation of the performance of a given

classification algorithm by investigating its

parameters. Zhou, L., et al (2008) assessed the

impacts of several internal parameters of the multi-

layer-perceptron (MLP) neural networks, they

reported that a number of internal parameters

significantly affect classification accuracy, and

proposed a guideline that can facilitate the use of

neural networks for land cover classification. Huang

et al (2002) compared the outcome of different sets of

parameters of the Polynomial and Radial Basis

Function Kernels. Keuchel et al. (2003) compared the

classification accuracy of SVMs, maximum

likelihood and iterated conditional modes (ICM), and

suggested that attention should be payed to SVM

parameters. One noteworthy mention to Yang, X.

(2011), who constructed a set of SVMs with different

combinations of Kernel types and parameters, to

classify a Landsat Thematic Mapper image, and

stated that the improvement of the performance of

classification, can in fact be obtained by a careful

selection of parameter settings.

Our objective being the assessment of the impact

of internal parameters of the theoretically robust

classification technique SVM (Kernel types, Pyramid

Level, Penalty parameter, Gamma Parameter, the bias

and the degree) on the performance of SVM for land-

cover classification using remote sensed data. We

examined the efficiency of this technique in

classifying S2 derived NDVI time-series from 21

dates of 2018. The images were acquired over the

Haouz plain, in central of Morocco, and classified

into six land-cover classes. The implementation of the

algorithms has been software-based, and the results

were validated and quantified using ground truth

information.

The present work started with an introduction

clarifying the importance and the motivations behind

the creation of detailed and accurate land cover maps.

Then, we illustrated the main materials and methods

used in this study. After that, the obtained results were

presented and discussed in the third section. Finally,

we ended this paper with the main conclusions and

perspectives.

2 MATERIAL AND METHODS

2.1 Site Location

The Haouz plain is located in the eastern part of the

Marrakech-Safi region in central Morocco. It extends

in the west-to-east direction between the High Atlas

Mountains in the south and Jebilat hills in the north.

It is characterized by a semi-arid climate, where the

annual average of the rainfall is about 250mm. It is a

predominantly rural area where the agricultural sector

plays an important role. The mainly consistent crop

types in the area are: Cereals, Citrus and olive trees.

2.2 Sentinel-2 Data

S2 is a series of earth-observation satellites carrying

multi-spectral imagery (MSI) optical sensors. The

free of charge, atmospherically and geometrically

corrected 10-, 20- to 60- meter images are acquired

every 5 days. 21 cloud free images, ranged over the

seasons from January to December of 2018 were

selected to derive the Normalized Difference

Vegetation Index (NDVI) time-series. The NDVI was

chosen for being an efficient and popular index for

monitoring the vegetation. It was first introduced by

Tucker (1979). The ground truth samples were

collected during the spring of the same year. All the

samples were divided into two groups using a

proportionate random sampling approach: calibration

data and validation data.

2.3 ENVI Software and SVM

Parameters

Software-based, automated classification algorithms

are widely used in the field of remote sensing. ENVI

is a powerful image analysis software, commonly

used in the remote sensing society. It includes a suite

of image analysis tools, among which a variety of

supervised and unsupervised classification

algorithms, and particularly the SVM classifier. The

choice of a parametrization is always presented

before starting the classification. Unfortunately, the

parameters are often left by not-familiar users in

“default mode”. As to our work, evaluating the effect

of the parametrization on the outcoming classified

images, and presenting a guideline that can help

parameterize the SVMs, was part of our interest.

Although users do not need to fully understand the

theory behind SVM, brief basics are introduced.

Support Vector Machine is derived from the

statistical learning theory, first introduced by Vapnik

in 1979, often gives satisfying results from large and

noisy data. It separates the classes with a decision

surface called the optimal hyperplane that maximizes

the margin between the classes. The original optimal

hyperplane algorithm was a linear classifier,

nevertheless, SVM can be adapted to become a

nonlinear classifier through the use of nonlinear

functions called Kernels (Cortes and Vapnik, 1995).

Considering a set of training samples (Xi, Yi), i =

1,……, n where Xi ϵ Rn and y ϵ {1,-1}n, SVM

optimizes the problem by searching for a large margin

and a small error penalty, from a mathematical point

of view (Cortes and Vapnik, 1995), it requires the

solution of:

𝑀𝑖𝑛

𝑤,𝑏,𝜀

𝑤

𝑇

𝑤𝑃 𝜀

𝑖

𝑛

𝑖1

Such that:

𝑌

𝑖



𝑤

𝑇

𝛷



𝑋

𝑖



𝑏



1 𝜀

𝑖

𝑎𝑛𝑑 𝜀

𝑖

0

Where Φ is a function that project Xi into a higher

dimension, and P is the Penalty parameter (P>0).

Although new Kernels are being proposed by

researchers, the basic Kernels considered in this study

include the ones implemented in ENVI: linear,

polynomial, radial basis function, and sigmoid:

- Linear: K (Xi , Xj) = XiT Xj.

- Polynomial: K (Xi , Xj) = (γ × XiT Xj + r) d , γ > 0.

- Radial basis function (RBF):

K (Xi , Xj) = exp (-γ ×||Xi – Xj ||²), γ > 0.

- Sigmoid: K (Xi , Xj) = tanh (γ × XiT Xj + r).

Where K (Xi , Xj) = Φ (Xi)T Φ (Xj), γ is the Gamma

parameter, d the Degree and r the Bias.

ENVI’s implementation of SVM includes the listed

above parameters, which are apparently dependent of

the Kernel Type. More details about the default and

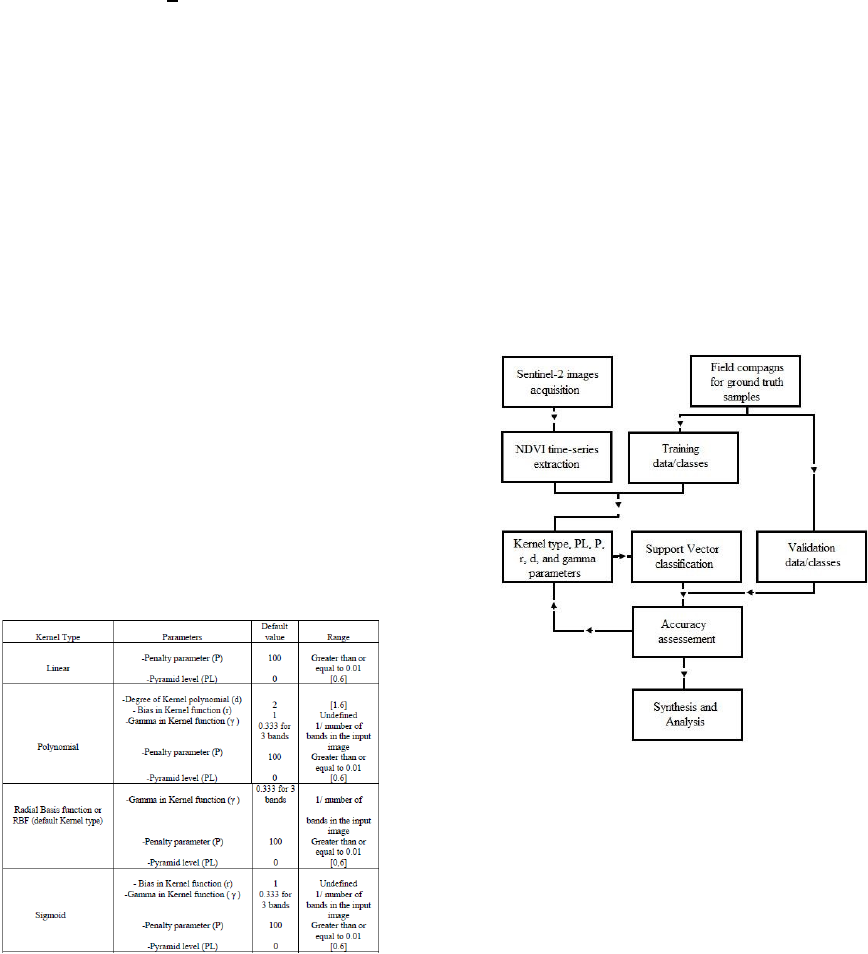
ranges values are presented in the table below.

Table 1. Kernel functions, Default values and variation

ranges of SVM in ENVI.

2.4 Methodology

The methodological approach for this study consists

mainly on applying different parameter combination

scenarios, with the same input NDVI time series and

the same training/validation samples. The accuracy

assessment was evaluated using the generated

confusion matrix. The resulting OA, Kappa and

running time of each model were noted and analyzed

for determining the effect of the different sets on the

classification outcome. The number of combinations

can reach thousands if not millions, therefore the

approach consisted on a similar technique used by

Zhou, L., et al (2008). They altered the value of one

NN’s parameter while holding the others unchanged,

a way to separately evaluate each parameter’s effect

on the resulting classification’s accuracy and Kappa,

or the work of Yang, X. (2011), where he used the

same methodology but for SVM classifier. The

difference in our approach, is that we regularize one

parameter until an optimum is reached, then it’s value

will be fixed for the rest, a way of ensuring the best

performance of the Kernels, the same process is

repeated to the next one until all the parameters values

are investigated (Figure 1). The default set of

parameters of each Kernel function are chosen as

starting scenarios.

Figure 1: The methodological approach of the procedure

followed in this study.

3 RESULTS AND DISCUSSION

The ultimate goal of this study was to assess how

internal parameters of support vector machines, can

affect land-cover classification, when used to classify

NDVI time-series. The final number of models

investigated is 85, and which depended on the

resulting accuracies. We followed the up and down

evolutions of the accuracies until it has been clear

where the optimum resides. Radial basis function,

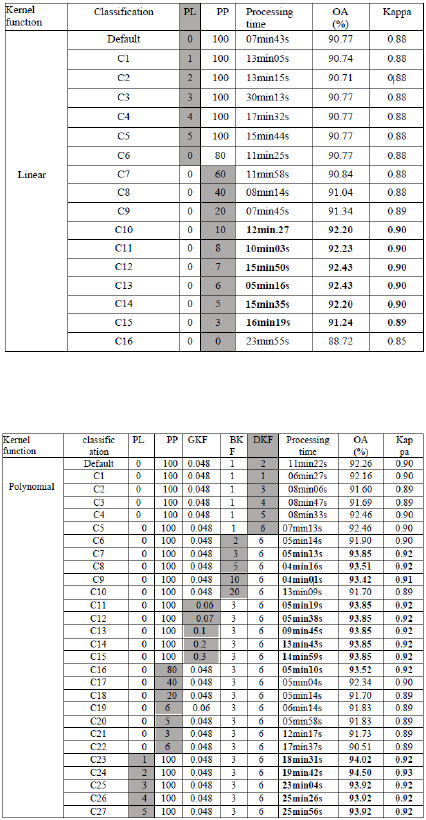
with a PL=0, a P=100, and Gamma=0.048, being the

default set of parameters for the SVM algorithm in

ENVI software, gave an OA of 92.76% and Kappa of

0.91(Table.4). While parameterizing the models, one

after another, we observed two important facts, the

first is: for all the four Kernel functions, the starting

configuration (Default parameters) increases by

varying the Penalty parameter for the linear and RBF

Kernel functions, the Degree and Bias for the

polynomial, and Gamma for the Sigmoid function.

The second fact is: generally, except for the

polynomial Kernel, increasing the Pyramid Level,

only decreases the OA, and surprisingly result in

more processing time (Tables.2-5). Polynomial

Kernel function, PL=2, P=100, Gamma=0.048, r=3

and d=6, resulted in the best accuracy and kappa in a

relatively good amount of processing time, and which

are of the order of 94.50% and 0.93 respectively

(Table.3).

For better visualization and analysis of the results,

figures 2, 3, 4 and 4 represent the variation of the OA

as the parameters are investigated. Flat areas reflect

the fact that the parameter in question doesn’t affect

the classification results at all. Meanwhile areas with

high slopes confirm that the parameter does affect the

outcoming results. A closer look to the results,

starting with the linear Kernel, we can summarize by

saying that, while it seems unaffected by the Pyramid

Level’s varying value, the OA increases when the

Penalty parameter decreases, and more specifically

when its value approaches the number of input

classes. It attains a maximum value of 92.43% and a

Kappa of 0.91 using this type of Kernel. The

polynomial Kernel is slightly sensitive to the degree

parameter, small fluctuations are observed, and the

OA increased as the degrees get greater, which is

consisting to the findings of Huang et al. (2002).

The Bias raised from 1 to 20 with non-regular

steps, and performed the best with a value of 3.

Gamma seemed to not affect the OA for values

between 0.048 and 0.3 and the performance was

rather stable. Meanwhile lowering the value of

penalty negatively affected it. A penalty of 2 helped

the polynomial Kernel to reach the best accuracy and

Kappa obtained for all the constructed models, which

equals 94.50 % and 0.93 respectively. The RBF

function, being the default Kernel, relatively to the

others, resulted in moderate OA, it’s affected the most

by the Penalty parameter and performed at its best

with a value of 60, namely, 92.99% OA and 0.91

Kappa. While Gamma does appear to generally not

affect the performance, raising the Pyramid Level

decreases it. And last, the Sigmoid function, similarly

to the RBF, performed best with a Penalty of 60, and

was quite sensitive when varying Gamma, still didn’t

improve. The best OA and Kappa found using this

Kernel is 92.99%.

Table 2: Overall accuracies, Kappa and processing time for

the linear Kernel type’s different combinations

Table 3: Overall accuracies, Kappa and processing time for

the Polynomial Kernel type’s different combinations.

Even though the OA and Kappa have increased

slightly when comparing the 85 models, given a large

area, the weight of this augmentation’s importance

can be great. For example, for a regular 100×100 Km

S2 image, for a spatial resolution of 10m, a 1.51% of

improvement represents about 1.51 million corrected

pixels, and an area of fifteen thousand one hundred

hectares. We mapped the best resulting classifications

for each of the four Kernel functions, obtained with

the optimal set of parameters.

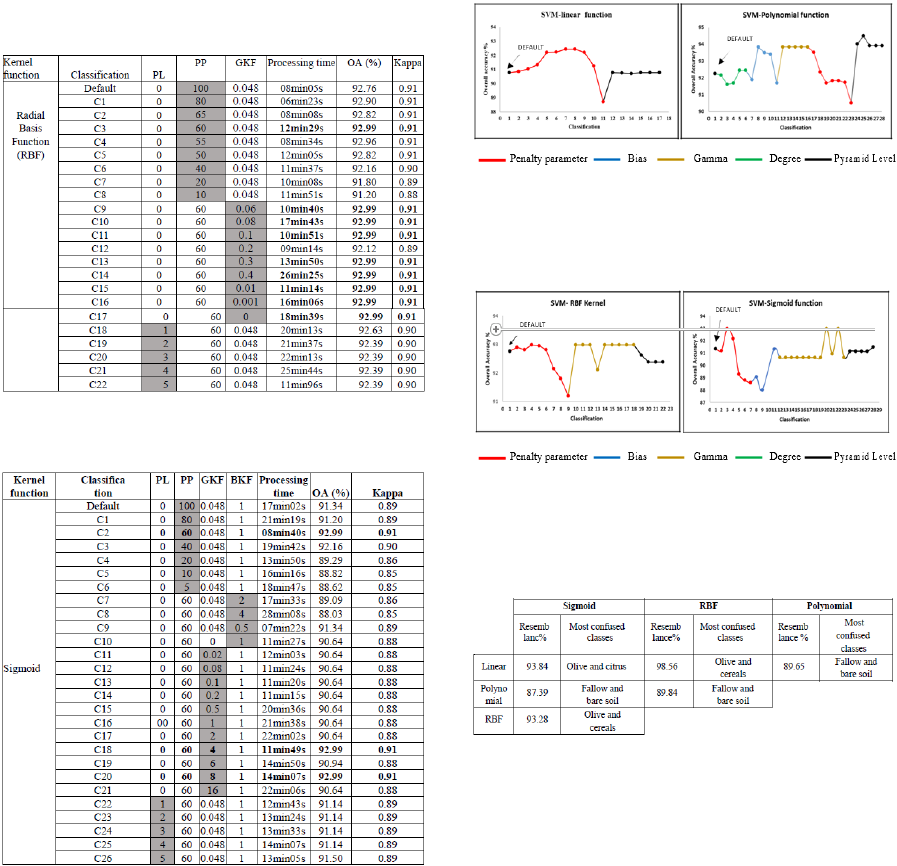
Table 4: Overall accuracies, Kappa and processing time for

the RBF Kernel type’s different combinations.

Table 5: Overall accuracies, Kappa and processing time for

the Sigmoid Kernel type’s different combinations.

Table 6 summarizes the percentage of

resemblance of the four maps and shows the most

confused classes. The Linear and RBF Kernels were

found to resemble each other the most, and hey both

performed like the Sigmoid Kernel more than the

Polynomial one. The nearest one to this latter, in

terms of performance is the RBF Kernel. A further

examination, shows that the classes that were

confused the most are fallow and bare soil, which is

natural, due to the fact that their spectral signatures

overlap, and not to mention that vegetation is absent

during the dry months.

Figure 2 and 3: To the left, combination of different

parameters using the Linear Kernel. To the right,

combination of different parameters using the polynomial

Kernel.

Figure 4 and 5: Combination of different parameters using

the RBF Kernel. To the right, Combination of different

parameters using the Sigmoid Kernel.

Table 6: Comparison of the four Kernels best combinations.

Additional experiments were done, using the

ground truth data of another area in the western part

of Haouz plain for the year of 2019. Seven thematic

classes were selected, including winter and summer

crops, for classification. The obtained results, with

standard parameters, gave an OA of 82.19 % and

kappa of 0.78. While, using the optimal parameters

obtained in this study, the classification accuracy

decreased and reached an OA of 72.06% and kappa

of 0.66. The main goal of these experiments is to

proof that such parameterization should be done for

each specific area depending on its land cover types.

4 CONCLUSIONS

This paper highlights the influence of SVM Kernel

types and internal parameters over the accuracy of the

land-cover classification of remote sensing data. 21

NDVI time-series derived from S2 images was used.

85 models were constructed from a combination of

four types of Kernels, between one to four Kernel

parameters (depending on Kernel’s type: The Penalty

parameter Gamma, the Bias and the Degree), and one

software-dependent parameter, the Pyramid Level.

Each model’s OA and Kappa coefficient were noted

and served as means of the performance evaluation.

The results showed that this techniques effectiveness,

does substantially depend on the Kernel’s choice and

the internal parameters combination. The polynomial

kernel outperformed the others, and attained, for

PL=2, P=100, r=3, d=6, and Gamma = 0.48, the best

OA and Kappa values: 94.50% and 0.93 respectively,

while the linear kernel performed the least with an

OA that can go down to 88.72% and Kappa of 0.85.

Overall, the models were quite sensitive to the

Penalty parameter and except for the polynomial

type, does not appear to improve when changing the

Pyramid Level, if not degrading the performance. We

hope that the work provided in the current paper,

would help as a guidance to applying SVM classifier

for the purpose of land cover classification of satellite

data, and encourage users to explore more the

different set of parameters. Further work would be

carried in exploring other powerful classifiers such as

the Neural Networks or the Random Forest.

REFERENCES

Anderson, M. C., Allen, R. G., Morse, A., & Kustas, W. P.

(2012). Use of Landsat thermal imagery in monitoring

evapotranspiration and managing water resources.

Remote Sensing of Environment, 122, 50-65.

Cortes, C., & Vapnik, V. (1995). Support-vector networks.

Machine learning, 20(3), 273-297.

Huang, C., Davis, L. S., & Townshend, J. R. G. (2002). An

assessment of support vector machines for land cover

classification. International Journal of remote sensing,

23(4), 725-749.

Keuchel, J., Naumann, S., Heiler, M., & Siegmund, A.

(2003). Automatic land cover analysis for Tenerife by

supervised classification using remotely sensed data.

Remote sensing of environment, 86(4), 530-541.

Khanal, S., Fulton, J., & Shearer, S. (2017). An overview

of current and potential applications of thermal remote

sensing in precision agriculture. Computers and

Electronics in Agriculture, 139, 22-32.

Khatami, R., Mountrakis, G., & Stehman, S. V. (2016). A

meta-analysis of remote sensing research on supervised

pixel-based land-cover image classification processes:

General guidelines for practitioners and future research.

Remote Sensing of Environment, 177, 89-100.

Lawley, V., Lewis, M., Clarke, K., & Ostendorf, B. (2016).

Site-based and remote sensing methods for monitoring

indicators of vegetation condition: An Australian

review. Ecological Indicators, 60, 1273-1283.

Li, C., Wang, J., Wang, L., Hu, L., & Gong, P. (2014).

Comparison of classification algorithms and training

sample sizes in urban land classification with Landsat

thematic mapper imagery. Remote Sensing, 6(2), 964-

983.

McDowell, N. G., Coops, N. C., Beck, P. S., Chambers, J.

Q., Gangodagamage, C., Hicke, J. A., ... & Meddens,

A. J. (2015). Global satellite monitoring of climate-

induced vegetation disturbances. Trends in plant

science, 20(2), 114-123.

Mishra, D., & Singh, B. N. (2019). Derivation of Magnitude

of Crop Diversity Through NDVI Composite Index

Using Sentinel-2 Satellite Imagery. Journal of the

Indian Society of Remote Sensing, 1-14.

Moumni, A., Sebbar, B., Simonneaux, V., Ezzahar, J., &

Lahrouni, A. (2019). Sample period dependent

classification approach for the cartography of crops in

the Haouz plain, Morocco. In Remote Sensing for

Agriculture, Ecosystems, and Hydrology XXI (Vol.

11149, p. 1114909). International Society for Optics

and Photonics.

Moumni, A., Sebbar, B. E., Simonneaux, V., Ezzahar, J., &

Lahrouni, A. (2020). Evaluation Of Sen2agri System

Over Semi-Arid Conditions: A Case Study Of The

Haouz Plain In Central Morocco. In 2020

Mediterranean and Middle-East Geoscience and

Remote Sensing Symposium (M2GARSS) (pp. 343-

346). IEEE.

Mulla, D. J. (2013). Twenty five years of remote sensing in

precision agriculture: Key advances and remaining

knowledge gaps. Biosystems engineering, 114(4), 358-

371.

Thanh Noi, P., & Kappas, M. (2018). Comparison of

random forest, k-nearest neighbor, and support vector

machine classifiers for land cover classification using

Sentinel-2 imagery. Sensors, 18(1), 18.

Tucker, C. J. (1979). Red and photographic infrared linear

combinations for monitoring vegetation. Remote

sensing of Environment, 8(2), 127-150.

Vapnik, V. N. (1979). Reconstruction of Dependences from

Empirical Data.

Wilkinson, G. G. (2005). Results and implications of a

study of fifteen years of satellite image classification

experiments. IEEE Transactions on Geoscience and

remote sensing, 43(3), 433-440.

Yang, X. (2011). Parameterizing support vector machines

for land cover classification. Photogrammetric

Engineering & Remote Sensing, 77(1), 27-37.

Yu, L., Liang, L., Wang, J., Zhao, Y., Cheng, Q., Hu, L., ...

& Li, X. (2014). Meta-discoveries from a synthesis of

satellite-based land-cover mapping research.

International Journal of Remote Sensing, 35(13), 4573-

4588.

Zhou, L., & Yang, X. (2008). Use of neural networks for

land cover classification from remotely sensed imagery.

The International Archives of the Photogrammetry,

Remote Sensing and Spatial Information Sciences, 37,

575-578.