
COVID19: Confinement Control based on a New Discrete
Localization Algorithm (DLA)
Yves Frederic Ebobisse Djene
1,2
, Rafiqa Zerououl
2
, Amine Berrazzouk
1
, Youness Chaabi
3
,
Fatima-Zahra Belouadha
4,5
, Younes Bekali Karfa
5,6
, Brahim El Bhiri
2
1
LARIT- IBN Tofail University, Kenitra, Morocco
2
SMARTiLab EMSI, Rabat, Morocco
3
CEISIC, IRCAM, Rabat, Morocco
4
EMI, Rabat, Morocco
6
Faculté des Sciences de Rabat
5
Mohammed V University in Rabat, Morocco
,bra.elbhiri}@gmail.com, y.bekali@um5r.ac.ma
Keywords: COVID-19, mobile Applications, Graph theory, Code QR, Confinement/Deconfinement.
Abstract: Mobile apps have potential to reinforce contact- tracing policies to cover and reverse the spread of COVID-
19. However, the majority of applications are based on the use of GPS, which have limitations linked to the
violation of data privacy. This finding is strongly refused by human rights NGOs. In this context, we propose
a concrete and operational digital solution related to epidemics including Covid-19, which is today the highest
international priority. This solution based on Discrete Localization Algorithm (DLA) is a complete and legal
intelligent solution to automate containment control and the deconfinement processes.
1 INTRODUCTION
The first case of the Corona virus epidemic (COVID-
19) procured in China (Wu, 2020), started at the end
of 2019 and quickly dispersed to the whole word.
Indeed, the mortality rate of Covid-19 is not as
high as that of MERS or SARS. However, it is a novel
virus with no effective cures or vaccines, which can
disrupt the public health systems. Moreover, most
Covid-19 patients in modest parts of the population
have to battle with severe pneumonia without crucial
life support, and thus leading to much higher fatality
rates (Ferguson, 2020).
Over the world, to curb the outbreak and stop the
spread of COVID-19, national governments
particularly implemented two approaches. The first
approach included rigorous social distancing
measures, such as the national lockdown (closing
down of schools, public places, closure of non-
essential commercial and industrial activities and a
ban on non-essential traveling). The main goal of this
strategy was to reduce contact between all types of
persons and subsequently control the reproduction
number R0, which is the average number of persons
affected by an infectious person. This methodology
was thoroughly implemented by China, effectively
conquering the epidemic in a couple of months, and
the method was thereafter adopted by most Western
countries. However, there has been no reports on the
strategies to implement after the Pandemic is tamed,
which leaves most of the population still vulnerable
to the virus and thus prone to a second wave of virus
propagation.
The second approach is mitigation: The idea is to
focus on slowing rather than stopping the spread of
the epidemic, leading to herd immunity, while
controlling it by protecting those at most risk of
serious illness from infection, in a way that ensures
the continuity of the public health system. This
approach initially spearheaded by (Hunter, 2020), has
been adopted by the UK government, which later
changed the strategy to transmission suppression after
the public release of the 9th related report from
Imperial College London (Ferguson, 2020).
Truly, other measures and procedures can be used
to control the mentioned index R0. For instance, the
use of digital and special mobile applications in
combating COVID-19 has been largely discussed and
suggested. These apps are designed to help contact
tracing and identifying persons in response to the
COVID-19 pandemic. In this perspective, several
applications were suggested, with official
government support in some countries. Several states
recognize that the value of such apps needs to be
considered within the context of wider public health
measures and the stage of the spread of the infection.
These mobile applications seem to be very interesting
as they can help in identifying the infected persons,
contact tracing and averting, symptoms checking and
contact notification contacts etc.
Since the beginning of the COVID-19 pandemic,
many smartphone apps have been developed, some of
them by public authorities. Moreover, the World
Health Organization (WHO) is working on an
application that can provide medically- approved
information and inform the users based on their
symptoms (WHO, 2020). This standalone application
comes besides the WhatsApp-based messaging
(WHO, August 2020).
However, the Covid-19 mobile apps must have
full compliance and ensure privacy legislation and
data protection. These Privacy worries have been
raised, especially about systems that are established
on tracking the geographical location of application
users. A of lot of measurements are taken to deal with
such problems, like the use of the anonymized data,
which does not consist of storing data in centralized
databases...
In the case of Morocco, the police have been using
a mobile application to follow on individuals that do
not respect the travel restrictions imposed to fight
Covid-19. With the same objective, we propose in
this study a new efficient system for controlling the
COVID-19 pandemic. This digital system is based on
a mathematical formalism to ensure confinement
control while respecting privacy data protection. This
solution can widely control the R0 parameter by
controlling the citizens mobility.
As presented in the following sections of this
paper, the proposed system uses a new concept called
the Discrete Localization Algorithm (DLA) and can
help to widely control R0 index with data protection.
The main objective of our system is twofold. On
one hand, it targets the authorization strategy control
and congestion suppression by automatically
generating authorizations to go out of the house or
those delivered by the job office with respect of the
data privacy. On the other hand, the system targets
data census by collecting information on people’s
mobility and compliance to confinement rules. Our
system therefore solves problems related to the time
delays in the measurements and control of the R0
parameter.
This study presents Graph theory and Minimum
Spanning Tree algorithm as well as details on the
Discrete Localization Algorithm (DLA), including
simulations.
2 GRAPH THEORY AND
MINIMUM SPANNING TREE
Our approach is based on graph theory and minimum
spanning tree. Thus, each city (region or country) can
be rep- resented by its corresponding undirected and
connected graph G(B; E) where B is the set of vertices
(nodes) representing different police control point,
and E is the set of links between nodes (itineraries).
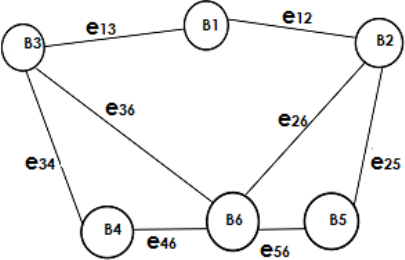
Each vertex of B is indicated by an index i € 1, ..., N.
e
ij
identifies the edge between the nodes B
i
and B
j
as
represented in figure 1.
For the connected graph G (B; E), the minimum
spanning tree (MST) problem is focused on finding a
spanning tree with minimum total edge weight. This
problem has been widely considered and is a sub-
problem of many known network problems. Its
applicable in wireless networks and VLSI design
(AFP, 2020), (Tseng, 1998), (Zheng, 1996) and many
graph problems such as connectivity checking (Maon,
1986), (Tarjan, 1985). It is also used on ovarian and
bronchial cancer detection and various other medical
analyses (Brinkhuis, 1997), and network evolvement
(Matos, 2002).
Boruvka, Kruskal, and Prim algorithms provide a
large number of the known algorithms. Since
Kruskals algorithm works on arranged edges and
MST edges are likely to be among the θ(nlog(n))
smallest weight edges, partial sorting of edges work
greatly to find out lighter edges (Brennan, 1982),
(Paredes, 2006).
Filtering of edges connecting nodes makes the
algorithm very faster (Kershenbaum ,1972).
Figure 1: An example illustrating an undirected graph
In addition, Bucket sorting on edges is employed
in Kruskal’s algorithm which performs greatly for
uniformly distributed random edge weights
(Katajainen, 1983).
A recently devised Filter-Kruskal algorithm has a
higher performance over a wide range of input types
(Osipov, 2009). Edge Pruned Minimum Spanning
Tree (EPMST) algorithm uses the benefits of
Kruskal’s and Prims algorithms. As Kruskal’s
algorithm performs better on sparse graphs and
produces a minimum spanning forest, EPMST filters
out a large number of edges before running the
Kruskal’s algorithm. Then it runs Prims algorithm on
a compact dense graph. Selection of pivot value is a
major concern on the EPMST (Mamun, 2016).
3 GRAPH THEORY AND
MINIMUM SPANNING TREE
The objective of this part is to define the relation
between controlled geographic space by the local
authorities and graph theory. In addition, we present
the DLA algorithm to control the confinement. Using
the graph theory and the Minimum spanning Tree we
can define:
Identification of the authorized area As: For
each displacement, an authorized area As is
generated. It’s based on the source and
destination positions and on the tolerated space
by the authorities. This area is computed using
Edge Pruned Minimum Spanning Tree
(EPMST) algorithm, which has a superior
performance relative to the best-known
algorithms especially when the graph is not
very sparse (Mamun, 2016). Moreover,
EPMST algorithm (Mamun, 2016) is also used
to select the shortest path and the tolerated
space by the authorities. Any control by the
agents of authorities inside the authorized zone
will be accepted and validated, except if there
the estimated duration for the displacement is
not exceeded. In addition, if the check is carried
outside this zone, the application automatically
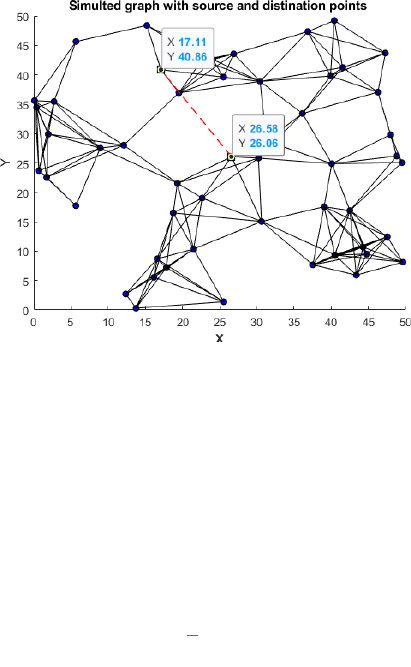
generates police fine. The figure 2 shows a
simulated graph highlighting the departure and
the arrival points demanded by the user. The
city is a 50km2 square with 50 control stations
represented as a network. Figure 3 represents
the shortest path between the source and
destination. This path is used to compute the
time duration authorised for the displacement if
the control stations are identified by a number
or a specific value. Figure 4 presents in addition
to the shortest path, the control station
identifications. Figure 6 resumes the ADL
solution based on the EPMST. It shows the
connected graph, the minimum weight
spanning tree and the shortest path. The Figure
5 illustrates a simulated graph highlighting the
shortest path between the departure and the
arrival points and the control stations identified
by values (codes). Besides, Figure 6 shows in
addition to the shortest path, the authorized
space for the concerned displacement. This
space is indicated by the nodes and paths in
pink color. Indeed, each control by authorities
in this region gives an accepted permission.
Figure 2: Simulated graph highlighting the departure and
arrival points
Computation of the duration of the
displacement: Our system also computes the
displacement duration based on the shortest
path. In this study and to simplify the process,
we used the mean duration of all paths from
source to destination.
The equation 1 represents this duration as:
𝑇𝑑
1
𝑗
𝑡
(1)
Where t
i
represents the source and destination. The
parameter j represents the total number of possible
paths without loops.
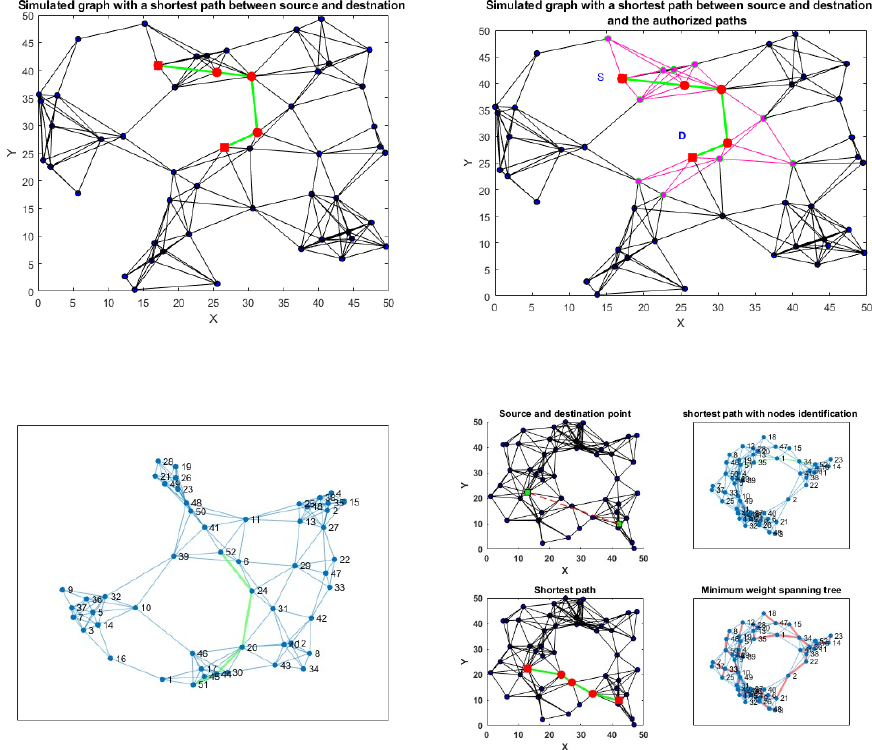
Figure 3: A Simulated graph with the shortest path between
source and destination points, 50 control station and 50x50
square region
Figure 4: Simulated graph the node identifiers and the
shortest path
4 SALAMATI APPLICATION
BASED ON THE DLA,
SIMULATION AND RESULTS
All citizens must download and correctly install the
SALAMATI Application (Figure 7) from the
internet space reserved for this operation. A person
going out for different reasons (to work, shop, or
buy medicine) must authenticate and identify the
destination. The authentication is based on the
National Identity Code (NIC) (CIN in the case of
Morocco) which is largely sufficient to identify all
persons. The application generates a QR code for
each service request.
Figure 5: Simulated graph highlighting the short paths and
the authorized area
Figure 6: Simulated graph highlighting the minimum
weight spanning tree and the shortest path
This code will be used for each control by the police
or authorities. The user can switch-off their internet
connection and only use the QR code generated by
the SALAMATI Application. This code contains
three types of data:
User Identification
The authorized area
Duration of the displacement.
For the control, while respecting social and
physical distance, the person presents the QR code to
the agent and the latter can then validate the real
position or not. The reader displays the NIC and two
different colors; green for approbation and red for no
authorization. The figures 8 and 9 show QR codes
generated by the SALAMATI Application and two
different responses for two different controls. The
first is rejected whereas the second is validated. The

agent must install the application SALAMATI for
lecture and control. In principle, internet connection
is not necessary, but can be used for centralizing data
and giving information about people’s mobility
compliance to confinement. In addition, this
parameter will be used for different uses, especially
in finding the relation between mobility and the R0
parameter.
Figure 7: SALAMATI Application
Figure 8: A non-authorized scanned localization
Figure 9: An authorized scanned localization
5 CONCLUSION
In this paper we propose a new approach to deal with
data privacy in the case of the confinement control.
This solution overcomes the limitations linked to the
violation of data privacy. We proposed a concrete and
operational digital solution to fight epidemics
including Covid-19, which is today the highest
international priority, based on a theoretical and
practical solution. Indeed, the SALAMATI mobile
application is based on the Discrete Localization
Algorithm (DLA) which is a complete and legal
intelligent solution to automate confinement control
processes and the progressive easing of lockdown by
controlling the displacement of citizens and the area
for which the authorization was delivered. The
SALAMATI mobile application is based on the QR
code solution identifying three parameters: a) User
Identification, b) The authorized area and c) Duration
of the displacement.
In the perspective works, we will measure time
computation and solve the congestion problem using
the SALAMATI mobile Application.
ACKNOWLEDGEMENTS
The authors would like to thank SMARTiLAB/EMSI
the High School of engineering group. This paper was
written within the scope of a COVID-19 project
supported by the supervisory ministry MENFPESRS
and the CNRST of Morocco with the aim of
prevention and forecast the spread of the COVID-19
pandemic (GRANT Number: COV/2020/87)
REFERENCES
AFP, 2020. La police marocaine lance une application
mobile pour traquer les déplacements. In Voaafrique.
https://www.voaafrique.com/a/maroc-virus-la-police-
lance-une- application-mobile-pour-traquer-les-
d%C3%A9placements/5386798.html
Brennan, J., 1982. Minimal spanning trees and partial
sorting. In Operations Research Letters, vol. 1, no. 3,
pp. 113-116.
Brinkhuis, M., Meijer, G. A., Van Diest, P. J., Schuurmans,
L. T., Baak, J., 1997. Minimum spanning tree analysis
in advanced ovarian carcinoma. an investigation of
sampling methods, reproducibility and correlation with
histologic grade. In Analytical and quantitative
cytology and histology, vol. 19, no. 3, pp. 194-201.
Ferguson, N., et al., 2020. Report 9: Impact of non-
pharmaceutical interventions (NPIs) to reduce
COVID19 mortality and healthcare demand, In
Imperial College London. doi:10.25561/77482
Hunter, D. J., 2020. Covid-19 and the stiff upper lip the
pandemic response in the United Kingdom. In the New
England Journal of Medicine, 382. doi :
10.1056/NEJMp2005755.
Katajainen, J., Nevalainen, O., 1983. An alternative for the
implementation of kruskals minimal spanning tree
algorithm. In Science of Computer Programming, vol.
3, no. 2, pp. 205-216.
Kershenbaum, A., Van Slyke, R., 1972. Computing
minimum spanning trees efficiently. In Proceedings of
the ACM annual conference. vol 1. pp. 518-527.
Mamun, A., Rajasekaran, S.,2016. An Efficient Minimum
Spanning Tree Algorithm, In Proceedings IEEE
Symposium on Computers and Communication (ISCC),
pp. 1047-1052
Maon, Y., Schieber, B., Vishkin, U., 1986. Parallel ear
decomposition search (eds) and st-numbering in graphs,
in VLSI Algorithms and Architectures. Springer, pp. 34-
45.
Matos, M., Raby, B. N., Zahm, J.-M., Polette, M.,
Birembaut, P., Bonnet, N., 2002. Cell migration and
proliferation are not discriminatory factors in vitro
sociologic behavior of bronchial epithelial cell lines, In
the Cell motility and the cytoskeleton, vol. 53, no. 1, pp.
53-65.
Meguerdichian, S., Koushanfar, F., Potkonjak, M.,
Srivastava, M., 2001. Coverage problems in wireless
ad-hoc sensor networks. In Proceedings IEEE
INFOCOM. Twentieth Annual Joint Conference of the
IEEE Computer and Communications Societies. vol. 3,
pp. 1380-1387
Osipov, V., Sanders, P., J., Singler, 2009. The filter-kruskal
minimum spanning tree algorithm. In ALENEX SIAM,
vol. 9, pp. 52-61.
Paredes, R., Navarro, G., 2006. Optimal incremental
sorting. In ALENEX. SIAM, pp. 171-182.
Tarjan, R. E., Vishkin, U., 1985. An efficient parallel
biconnectivity algorithm. In SIAM Journal on
Computing, vol. 14, no. 4, pp. 862-874.
Tseng, Y.-C., Juang, T. T.-Y., Du, M.-C.,1998. Building a
multicasting tree in a high-speed network. In IEEE
Concurrency, vol. 6, no. 4, pp. 57-67
Wu, Z., McGoogan, J. M.,2020. Characteristics of and
Important Lessons From the Coronavirus Disease 2019
(COVID-19) Outbreak in China: Summary of a Report
of 72 314 Cases From the Chinese Center for Disease
Control and Prevention.In JAMA. 323(13), pp 1239-
1242
WHO, 2020.Covid-19 App.
https://worldhealthorganization.github.io/app/.
WHO, August 2020. https://www.who.int/news-
room/feature-stories/detail/who-health-alert-brings-
covid-19-facts-to-billions-via-whatsapp
Zheng, S.-Q., Lim, J. S., Iyengar, S. S., 1996. Routing using
implicit connection graphs [vlsi design], In
Proceedings 9th International Conference on VLSI
Design, Bangalore, India, pp. 49-52.
