
Particles from Volcanic Scoria Powders: Granulometry and
Granulomorphology Data Analysis
Willy Hermann Juimo Tchamdjou
1
*, Azzeddine Bouyahyaoui
2
, Moulay Larbi Abidi
2
, Toufik
Cherradi
2
and Didier Fokwa
3
1
Department of Civil Engineering and Architecture, National Advanced School of Engineering, University of Maroua,
Maroua, Cameroon
2
Department of Civil Engineering, Mohammed School of Engineers, Mohammed V University of Rabat, Rabat, Morocco
3
Department of Civil Engineering, Higher Technical Teachers’ Training College, University of Douala, Douala, Cameroon
Keywords: Volcanic scoria powder, particle, granulometry, granulomorphology and data analysis.
Abstract: This study presents size and shape parameters relevant to volcanic scoria powder characterization. Particle
size distribution was compared using two different techniques, including laser diffraction and automated static
image analysis, and their respective results were discussed. Specific information on particle shape has been
obtained using image analysis by 2-D images. The image analysis was used to identify key controls on particle
morphology, six shape parameters: elongation, circularity, solidity, roughness, bluntness and luminance have
effectively accounted for the morphological variance of powder particles. The effect of the number of particles
of testing samples on these variables obtained through the image analysis was investigated. To develop
analytical models, Multiple linear regressions analysis was applied using the dataset. The dataset comprised
size and shape information’s about 24,268 particles from black natural powder, 32,302 particles from dark
red natural powder, 22,562 particles from red natural powder and 25,041 particles from yellow natural powder.
The analysis allowed us to identify the explanatory variables and develop eight mathematical models and
three of these models are intended to prediction with very good significance. The correlation coefficients and
analysis of variance test results obtained evidence the adequacy level of models. Thus, it is possible to estimate
each dependent response parameter through the proposed models.
1 INTRODUCTION
In the past few years, several studies have been
published that focused on the characterization of
maximum packing of supplementary cementitious
materials (SCMs) in cement-based systems. The
related works generally classified the factors that
affect the matrix compactness into four groups:
particle morphology, particle packing, interparticle
spacing and matrix rheology (Felekoglu. 2009;
Arvaniti et al, 2015a; Bouyahyaoui et al, 2018).
Particle size and particle shape are closely related to
the reactivity of SCMs. Industrial by-products, their
partial replacement of cement in concrete mixes
represents a substantial offset by the consequent
environmental impact. The size and shape
characterization of irregular particles is a key issue in
many fields of science (Bagheri et al, 2015) and
engineering (food, pharmaceutics, minerals, biology,
astronomy, …), which is often associated with large
uncertainties (Felekoglu. 2009; Bouyahyaoui et al,
2018; Bagheri et al, 2015; Liu et al, 2015; Dioguardi
et al, 2018). The main characteristics of powders are
the particle size (granulometry) and particle shape
(morphology). Technological properties of powders
depend on their granulometry and particle
morphology (Pavlović et al, 2010).
To date, only a few studies have been published
on particle size and particle shape parameters of
mineral powders using as SCMs (Felekoglu. 2009;
Bouyahyaoui et al, 2018; Bagheri et al, 2015 ;
Hackley et al, 2004 ; Michel and Courard, 2014 ;
Klemm and Wiggins, 2017). Technological
properties of mineral powders (bulk density,
flowability, surface area, etc.), as well as the potential
areas of SCMs, depend on these characteristics (Mikli
et al, 2001). It also has been known that powders may
improve the particle packing density of cementitious
system, and superplasticizers help to obtain the
desired rheological properties by increasing the
workability without causing segregation in fresh state
(Bouglada et al, 2019) and improve the mechanical
properties and durability by reducing the
water/cement ratio. Some of these powder materials
are either industrial by-products or unprocessed
materials. They provide environmental relief because
industrial by-products are being recycled and
hazardous emissions released into the atmosphere due
to cement production are reduced, raw materials are
preserved and energy is saved (Felekoglu. 2009).
Besides, inert and semi-inert powders such as
grounded volcanic scoria can be alternatively
employed for high-performance mortar and concrete
mixture designs (Juimo et al, 2017). More recent
works have addressed the effects of volcanic scoria
powder addition on rheological properties of cement
paste (Bouglada et al, 2019; Tchamdjou et al, 2017a;
Tchamdjou et al, 2017b).
Powders are problematic materials in the
application of particle size analysis (Felekoglu.
2009). In general, sizing techniques work best over a
limited size range. The optimum range of particle size
analysis varies according to many factors, including
detector sensitivity and the assumptions associated
with the underlying principle of measurement
(Felekoglu. 2009; Arvaniti et al, 2015b).
Most commercial methods are designed
specifically for a range of particle size, and work best
with homogeneous spheres. The degree to which
irregularity affects the results vary with the technique
employed, and is not well understood or exactly
accounted for in many methods (Felekoglu. 2009;
Bagheri et al, 2015 ; Orhan et al, 2004; Ferraris et al,
2002).
The morphology of raw powder includes its
particle size distribution (PSD), specific surface area
(𝑆
or 𝑆
) and particle shape. The PSD can be
determined by sieves analysis, laser diffraction (LD)
and image analysis (IA). The industrial method to
determine 𝑆
is Blaine Air Permeability test
(Arvaniti et al, 2015a; Niesel. 1973). The evaluation
of particle shape needs complex techniques such as
the LD and the IA (Bagheri et al, 2015; Arvaniti et al,
2015b). Individual particle features should be
captured by IA to derive the shape descriptors
(Bouyahyaoui et al, 2018; Abazarpoor et al, 2017; Ilic
et al, 2015).
In this study, the particle shape and surface
morphology of volcanic scoria powders (ground at
different grades) data were analyzed.
2 EXPERIMENTAL DATA
2.1 Powders Samples
Four volcanic scoria groups according to the color of
scoria have been collected. The collected sample was
firstly sieved using the 5 mm stainless steel sieve of
20 cm diameter to separate large volcanic scoria (5–
100 mm in order) to fine volcanic scoria (≤5 mm).
The volcanic scoria sample was performed on the
material dried in an open air environment during 24 h
and in the oven at 105 °C during 24 h for the removal
of moisture in the rocks (Juimo et al, 2016).
The mill process was performed for 20 minutes.
Milling sample has been introduced at the same
weight for each production. The rotation speed of the
mill was about 70 rpm (Bouyahyaoui et al, 2018).
Each powder obtained has been described by a two-
component code designation: the letter reflecting
powder color as black (B), dark-red (DR), red (R) and
yellow (Y) followed by the ‘np’ reflecting natural
powder or natural pozzolan (Juimo et al, 2017).
2.2 Measurement Methods
2.2.1 Gas Pycnometer and Blaine Air
Permeability (Blaine Fineness, BF)
In this work, the density of powders was performed
on a Gas Pycnometer. This method measures the
density by determining the volume of inert gas that
can be introduced into a sample chamber of a defined
size which contains a known mass of powder.
Automatic Gas Pycnometer has long been identified
as the instrument of choice to accurately measure the
true density of solid materials by employing
Archimedes’ principle of fluid displacement, and
Boyle’s Law of gas expansion (Niesel. 1973; EN 196-
6, 2010). Helium inert gas, rather than a liquid, is used
since it will penetrate even the finest pores and
eliminate the influence of surface chemistry. This
ensures quick results of the highest accuracy.
The fineness of the grinding was being
determined according to the Blaine technique and is
indicated as the specific surface (Blaine fineness
value). The Blaine Air Permeability apparatus serves
exclusively for the determination of the specific
surface area (𝑆
) of powders. The Blaine Fineness
(BF) value is not a measure of granulometric
distribution (Means PSD).
2.2.2 Laser Diffraction (LD)
The granulometry of powders was determined by
many methods (sieve analysis, LD, IA, etc.), but the
question is how adequately they describe the powder
granulometry (Mikli et al, 2001). Mikli et al. (Mikli
et al, 2001) reported that the evaluation of the fine
powder granulometry (with particle size less than 50
μm) is more difficult and the results of the sieve
analysis do not describe adequately the powder
granulometry. For this reason, the first method used
here to describe powder granulometry is LD. LD
which is based on a complex theory of interaction
between monochromatic light and individual
particles. This involves the detection of the angular
distribution of light scattered by a set of
monodispersed spherical particles to provide a
‘sphere’-equivalent size diameter distribution using a
reverse optical scattering-based model calculation
(Michel and Courard, 2014).
In LD, the angular distribution of light is
measured after passing through an optically dilute
dispersion of suspended particles. The LD system
determines the PSD based on a volumetric basis.
Different optical models are commonly used to build
the PSD weighted by apparent volume (volume of an
equivalent sphere of diameter D), such as Mie theory-
based and Fraunhofer models (Michel and Courard,
2014; Varga et al, 2018).
2.2.3 Image Analysis (IA)
IA has made a decisive breakthrough in the recent
years to become a reference technique in the field of
combined size and shape analysis of particles
(Arvaniti et al, 2015b; Gregoire et al, 2007). The IA
is a method for the measurement of particle size and
shape distributions. For the measurement of particle
size and morphometric characterization, an Occhio
500 Nano image analyzer has been used. The
morphology of a powder particle is characterized by
shape description (elongation, circularity, solidity,
roughness, bluntness (with the calypter), luminance)
or quasi-quantitatively, for example, by means of
geometrical shape parameters.
The IA is based on the measurement of each
particle; the accuracy of a size and shape distribution
has to be formulated in number of particles (𝑁
) and
not in terms of sample weight or duration of the
analysis. The adequate particle number is linked to
the shape of the distribution curve and its extension
or range (Gregoire et al, 2007). Volcanic scoria
powders tested by the IA had respectively: 24,268
particles for Bnp, 32,302 particles for DRnp, 22,562
particles for Rnp and 25,041 particles for Ynp.
3 DATA ANALYSIS METHODS
Data sets obtained by experimental analysis were
studied using SPSS software to understand the
influence and the correlation of different considerable
parameters (factors). The analysis of the individual
influence of a given factor in the description of a
complex phenomenon, such as the max distance
(𝑋
) or geodesic length (𝑋
) of the powder particle
can lead to erroneous conclusions; for example a
given factor could seem extremely relevant when it is
not. Slinker and Glantz (Slinker and Glantz, 2008)
and Neves et al. (Neves et al, 2018) reported that, a
given variable may appear unrelated to the dependent
variable when analyzed alone, but may have a strong
influence when considered simultaneously with other
predictors. To model and identify the main factors
that influence the other size parameter descriptors in
particle max distance and geodesic length, a multiple
linear regression (MLR) analysis is used, which
makes if possible examine the simultaneous effects of
multiple of independent predictor variables (IPVs) in
the variability of the dependent or explained variable
(Neves et al, 2018).
Table 1: Definitions of response variables and IPVs in the
systems.
Variable/Definition
𝑌 or
𝑌
Max Distance (𝑋
), Geodesic length (𝑋
),
Powdering ratio index by Blaine (𝑃𝑟
𝑁
𝑆
𝐷
⁄
) or Powdering ratio index by
LD (𝑃𝑟
𝑁
𝑆
𝐷
⁄
).
Var. Definition Variable Definition
𝑥
Inner Diameter
(𝑋
)
𝑦
Elongation (𝐸
)
𝑥
Area Diameter
(𝑋
)
𝑦
Circularity (𝐶
)
𝑥
Width (𝑊
) 𝑦
Solidity (𝑆
)
𝑥
Length (𝐿
) 𝑦
Roughness (𝑅
)
𝑥
Max Distance
(𝑋
)
𝑦
Luminance
(𝐿
)
𝑥
Geodesic length
(𝑋
)
𝑦
Bluntness (𝐵
)
This study also aimed to evaluate the potential
relationship between dependent variables (i.e., 𝑋
;
𝑋
; 𝑃𝑟
or 𝑃𝑟
) and input variables (i.e., 𝑋
;
𝑋
; 𝑊
; 𝐿
; 𝑋
; 𝑋
; 𝐸
; 𝐶
; 𝑆
; 𝑅
; 𝐿
; 𝐵
) by
applying statistical models. The independent
variables 𝑃𝑟
and 𝑃𝑟
expresses by 𝑁
𝑆
𝐷
⁄
and 𝑁
𝑆
𝐷
⁄
, and represent powdering ratio
index of powders by BF and LD respectively.
The explanatory variables included in models are
: 𝑋
; 𝑋
; 𝑊
; 𝐿
; 𝑋
; 𝑋
; 𝐸
; 𝐶
; 𝑆
; 𝑅
; 𝐿
and 𝐵
. Besides the conventional linear regression
model, introduced as Model 1(with 4 IPVs) and
Model 2 (with 5 IPVs) in Equation (1) based on the
linear regression model provide by Neves et al.
(Neves et al, 2018) and Jin et al. (Jin et al, 2018).
𝑌
𝑓
𝑥
→𝑌 𝛼
∑
𝛼
𝑥
𝜀
𝛼
𝛼
𝑥
𝛼
𝑥
∙ ∙ ∙ 𝛼
𝑥
𝜖
(1)
where 𝑌 represents the dependent variable (also
called response variable, output, endogenous or
explained), 𝛼
, 𝛼
, . . ., 𝛼
the regression
coefficients, 𝑥
, 𝑥
, . . ., 𝑥
the IPVs (Table I) and 𝜖
the random errors of the model.
Table 2: Description of the multiple linear regression model.
Equation
/Model
n°
IPVs used to predict Max
Distance (𝑋
)
IPVs used to predict
Geodesic length (𝑋
)
IPVs used to predict
Powdering ratio index by
Blaine (𝑃𝑟
𝑁
𝑆
𝐷
⁄
)
IPVs used to predict
Powdering ratio index
by LD (𝑃𝑟
𝑁
𝑆
𝐷
⁄
)
Eq.
(1)
1
𝑋
,𝑋
,𝑊
,𝐿
- - -
2
𝑋
,𝑋
,𝑊
,𝐿
,𝑋
𝑋
,𝑋
,𝑊
,𝐿
,𝑋
- -
Eq.
(2)
3
𝑋
, 𝑋
𝐸
, 𝑋
𝐶
, 𝑋
𝑅
,𝑋
𝑆
,𝑋
𝐿
,𝑋
𝐵
4
𝑋
, 𝑋
𝐸
,𝑋
𝐶
, 𝑋
𝑅
,𝑋
𝑆
,𝑋
𝐿
,𝑋
𝐵
5
𝑊
, 𝑊
𝐸
, 𝑊
𝐶
, 𝑊
𝑅
, 𝑊
𝑆
,𝑊
𝐿
,𝑊
𝐵
6
𝐿
, 𝐿
𝐸
, 𝐿
𝐶
, 𝐿
𝑅
, 𝐿
𝑆
,𝐿
𝐿
,𝐿
𝐵
7 -
𝑋
,𝑋
𝐸
,𝑋
𝐶
,𝑋
𝑅
,𝑋
𝑆
,𝑋
𝐿
, 𝑋
𝐵
8
𝑋
, 𝑋
𝐸
,𝑋
𝐶
, 𝑋
𝑅
, 𝑋
𝑆
, 𝑋
𝐿
, 𝑋
𝐵
-
𝑋
,𝑋
𝐸
,𝑋
𝐶
,𝑋
𝑅
, 𝑋
𝑆
,𝑋
𝐿
,𝑋
𝐵
The regression equation given by Equation (1)
gives the value predicted for the dependent variable
according to the IPVs included in the model, which
lies on the best-fit regression plane, which represents
the multidimensional generalization of a line (Slinker
and Glantz, 2008; Neves et al, 2018).
In this research we also proposed alternative non-
linear models to improve the determination
coefficients when predicting dependent variables
(Model 1 & 2: Multi-linear regression analysis).
These models range from Model 3 to Model 8 in
Equation (2), where 𝑖 1,∙ ∙ ∙ , 6 denotes the number
of IPVs concerning particle size descriptors. The
analysis of the interactions between size and shape
parameters in the description the max distance or
geodesic length of the powder particle, a MLR
analysis is used, which allows examining the
simultaneous effects of multiple IPVs in the
variability of the dependent or explained variable
with variables interact.
The statistical relationship between the dependent
variable 𝑌
and the multiple IPVs 𝑥
and 𝑦
is given
by Equation (2) (Model 3 to 8: Non-linear model
involving variables interactions).
𝑌
𝑓
𝑥
,𝑦
→𝑌
𝛽
∑
𝛽
𝑥
𝑦
𝜀 𝛽
𝛽
𝑥
𝑦
𝛽
𝑥
𝑦
∙ ∙ ∙
𝛽
𝑥
𝑦
𝜖
(2)
where 𝑌
represents the dependent variable (also
called response variable, output, endogenous or
explained, 𝑖 1,∙ ∙ ∙ ,𝑛 ), 𝛽
, 𝛽
, . . ., 𝛽
the
regression coefficients, 𝑥
and 𝑦
, 𝑥
,. . ., 𝑦
the
independent variables (Table 1) and 𝜀 the random
errors of the model.
The regression equation given by Equation (2)
gives the value predicted for the dependent variable
according to the IPVs included in the model which
lies on the best-fit regression plane that represents the
multidimensional generalization of a line (Slinker and
Glantz, 2008; Neves et al, 2018).
Among the k independent predictor variables
(IPVs), some may have more significant effects on
the target response variable than others as reported by
Jin et al. (Jin et al, 2018). In the same way, the t-test
of correlation analysis was used to determine the
significance regarding the effect of each IPV on the
response variable in this study. There is a p-value
corresponding to each t-value for an IPV. At the 95%
confidence level, a p-value lower than 0.05 would
indicate that this selected IPV makes a significant
contribution to the response variable. In contrast,
IPVs with p-values higher than 0.05 are those without
significant contributions. A possible reason why
some IPVs had higher significance than others was
the strong internal correlation among IPVs, which
caused redundancies. Therefore, the regression

analysis could be redone by removing the redundant
IPVs, shortening the equation to include only
significant IPVs. Target models, response variables
and various IPVs using input systems are defined in
Table 1 and Table 2.
Figure 1: Summary of production process and main testing data of powders.
4 RESULTS AND DISCUSSION
4.1 Principal Properties
The powders obtained have a density between 2.8 and
3.1 g/cm
3
and SSA Blaine between 3,500 and 5,300
cm
2
/g, which are comparable to ordinary Portland
cement fineness ((Bouyahyaoui et al, 2018; Juimo et
al, 2017).
By LD, mean particle diameter (Dmed), mean
particle diameter of 10% of particles D(10), median
particle diameter D(50) and mean particle diameter of
90% of particles D(90) were measured to evaluate the
efficiency of the milling process. Using the PSD data
obtain by LD and Equations (1)-(2), 𝑆
evaluated are
ranging between 4,400 to 6,000 cm
2
/g. 𝑆
value
obtains by this method for each powder is always
higher, that is about 4% to 25% than 𝑆
obtain by BF
(Figure 1).
PSDs of powders were evaluated by using the LD
and IA (Figure 1). In the LD technique, the angular
distribution of light is measured after passing through
an optically dilute dispersion of suspended particles.
This technique is widely used in dust and mineral
industry with water and dispersive agent to a special
cell where the laser light is sent (Felekoglu, 2009;
Orhan et al, 2004).
The inscribed disk diameter (𝑋
or 𝑋
) of each
particle is calculated in real time to build PSD curves
weighted by apparent volume (Gregoire et al, 2007),
making the assumption that particles have identical
flatness ratios, whatever their size (Michel and
Courard, 2014). Area diameter of particles was used
to plot PSD curve obtained by IA. The PSD profile
shows a negligible difference in the results by the two
methods (Abazarpoor et al, 2017). The main reasons
for differences between two PSD methods are as
follows: the considerate particle diameter by each
measurement process, the different shapes of the
particles; better insight into particles using the IA
method; insufficient dispersion of fine particles; fine
particles adhering to the bigger particles. LD and 2D
projection image by the IA are commonly used the
PSD measurement techniques, but the results may not
be representative of the strongly true physical
dimensions of the particles (Califice et al, 2013).
4.2 Particle Morphology Analysis
More than 50 images of powder particles were
identified. The particle morphology was found to
provide reasonable accuracy for estimating the
particle sizes of highly porous particles, where the
distinction between inter-particle and intra-particle
porosity was made. This important comment
concerning inter-particle and intra-particle porosity
has been also reported by Klemm and Wiggins
(Klemm and Wiggins, 2017).
4.2.1 Particle Morphology: Size Parameters
Distribution
Figure 2 shows the general identification of particles
according to their inner diameter and area diameter.
About 25% of Bnp particles, 25% of Ynp particles,
25% of DRnp particles, 25% of Bnp and 5% of Bnp
particles have the same area diameter like
respectively a particle n°1, n°2, n°3, n°4 and n°5 as
showing in Figure 2. In the same way, about 5% of
DRnp particles, 5% of Bnp particles, 6% of Rnp
particles, 6% of Ynp and 25% of Ynp particles have
the same area diameter like respectively a particle
n°1, n°2, n°3, n°4 and n°5 as showing in Figure 2.
Figure 2: Identification of particles based on their inner
diameter and area diameter.
Particles who have a high inner diameter and area
diameter are from DRnp powder and Particles who
present a very few inner diameter and area diameter
are from Rnp and Ynp powders.
Figure 3: Relation between (a) inner and area diameter, (b) width and length and (c) max distance and geodesic length consider
all powders.
Figure 3a shows that for all data obtained for all
powders, inner diameter and area diameter are well
related with a coefficient of correlation up to 0.99.
Figure 4 shows the general identification of
particles according to their inner diameter and area
diameter. About 25% of Bnp particles, 25% of DRnp
particles, 25% of Bnp particles, 6% of Ynp and 5% of
Bnp particles have the same width as particles n°11,
n°12, n°13, n°9 and n°7 respectively as shown in
Figure 4.
In the same way, about 5% of DRnp particles, 5%
of Rnp particles, 25% of Rnp particles, 25% of Rnp
and 25% of Ynp particles have the same length as
particles n°6, n°14, n°8, n°15 and n°16 respectively
as also shown in Figure 4. Particles that have a higher
width are from DRnp powder and those that present a
higher length are from Ynp powder. Particles that
present a very few width and length are from Rnp and
Ynp powders. Figure 3b shows that for all data
obtained for all powders, width and length are well
related with a coefficient of correlation up to 0.98.
Figure 4: Identification of particles based on their width and
length.
Figure 5 shows the general identification of
particles according to their max distance and geodesic
length. About 25% of Bnp particles, 25% of DRnp
particles, 25% of Bnp particles, 5% of Rnp and 5% of
DRnp particles have the same max distance as
particles n°11, n°17, n°18, n°14 and n°6 respectively
as shown in Figure 5. In the same way, about 5% of
Ynp particles, 5% of Bnp particles, 25% of Rnp
particles, 25% of Rnp and 25% of Ynp particles have
the same geodesic length as particles n°19, n°20,
n°21, n°22 and n°23 respectively as also shown in
Figure 5.
Figure 5: Identification of particles based on their max
distance and geodesic length.
Particles that have a higher max distance are from
DRnp and Ynp powders and whose who present a
higher geodesic length are from DRnp powder.
Particles that present a very few max distance and
geodesic length are from Rnp and Ynp powders.
Figure 3c shows that for all data obtained for all
powders, max distance and geodesic length are well
related with a coefficient of correlation up to 0.97.
4.2.2 Particle Morphology: Shape
Parameters Distribution
Figure 6 shows the general identification of particles
according to their elongation and circularity. About
4% of DRnp particles, 9% of Bnp particles, 25% of
Ynp particles, 25% of DRnp and 6% of Ynp particles
have the same circularity as particles n°6, n°24, n°25,
n°26 and n°27 respectively as shown in Figure 6.
Figure 6: Identification of particles based on their
elongation and circularity.
In the same way, about 5% of Ynp particles, 5%
of Rnp particles, 25% of DRnp particles, 25% of Bnp
and 25% of DRnp particles have the same elongation
as particles n°19, n°14, n°28, n°11 and n°17
respectively as also shown in Figure 6. Particles that
have a higher elongation are from Rnp and Ynp
powders and those that present a higher circularity are
from Rnp and Ynp powders. Particles that present a
very few elongation and circularity are from Bnp and
DRnp powders.
Figure 7 shows the general identification of
particles according to their roughness and solidity.
About 6% of Bnp particles, 6% of DRnp particles, 5%
of DRnp particles, 5% of Rnp and 6% of Ynp
particles have the same roughness as particles n°29,
n°30, n°31, n°32 and n°19 respectively as shown in
Figure 7.
In the same way, about 25% of Rnp particles, 25%
of DRnp particles, 25% of Ynp particles, 25% of Bnp
and 25% of DRnp particles have the same solidity as
particles n°33, n°17, n°25, n°7 and n°6 respectively
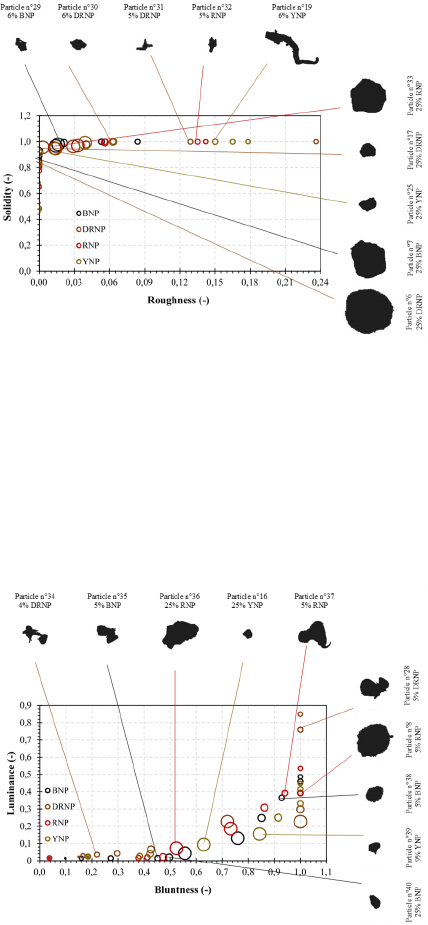
as also shown in Figure 7. Particles that have a higher
roughness are from Ynp powder. Particles that
present a very few roughnesses are also from Ynp
powder. These powder particles have in general a
solidity value equal to 1.0. This means that these
particles from volcanic scoria have a higher solidity.
Figure 7: Identification of particles based on their
roughness and solidity.
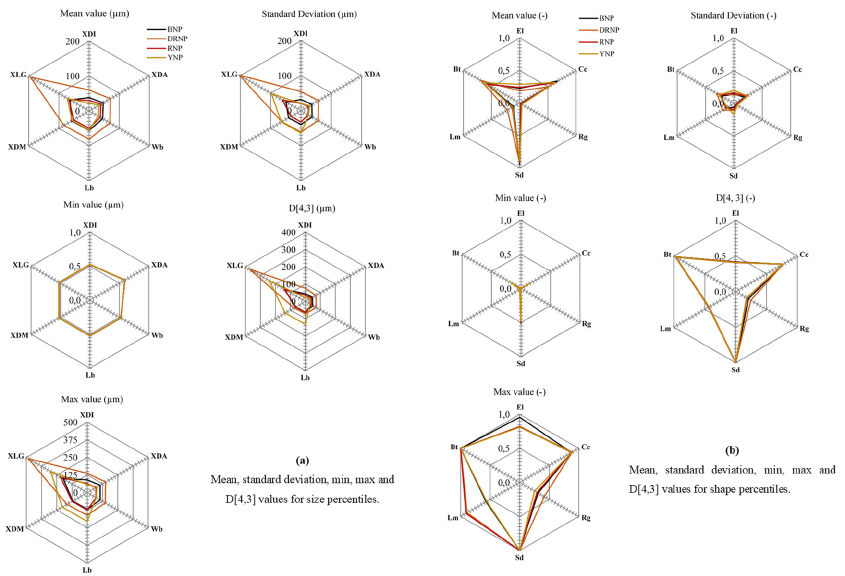
Figure 8 shows the general identification of
particles according to their luminance and bluntness.
About 4% of DRnp particles, 5% of Bnp particles,
25% of Rnp particles, 25% of Ynp and 5% of Rnp
particles have the same bluntness as particles n°34,
n°35, n°36, n°16 and n°37 respectively as shown in
Figure 8.
Figure 8: Identification of particles based on their
luminance and bluntness.
In the same way, about 5% of DRnp particles, 5%
of Rnp particles, 5% of Bnp particles, 9% of Ynp and
25% of Bnp particles have the same luminance as
particles n°28, n°8, n°38, n°39 and n°40 respectively
as also shown in Figure 8. Particles that have a higher
luminance are from DRnp powder. Particles that
present a very few luminance are from Rnp and Bnp
powders.
4.3 Study the Correlation Between
Several Parameters
In this study, the two major input systems within
volcanic scoria powder particle morphology (i.e., size
and shape input systems) were compared for their
accuracy in predicting considered dependent variable.
In addition, the effect of number of particle
projections (𝑁
) on the variables obtained through IA
is investigated.
The bestfit models were identified under each
input system. By removing significantly correlated
IPVs within each input system, the regression
modelling process was rerun by shortlisting (Jin et al,
2018).
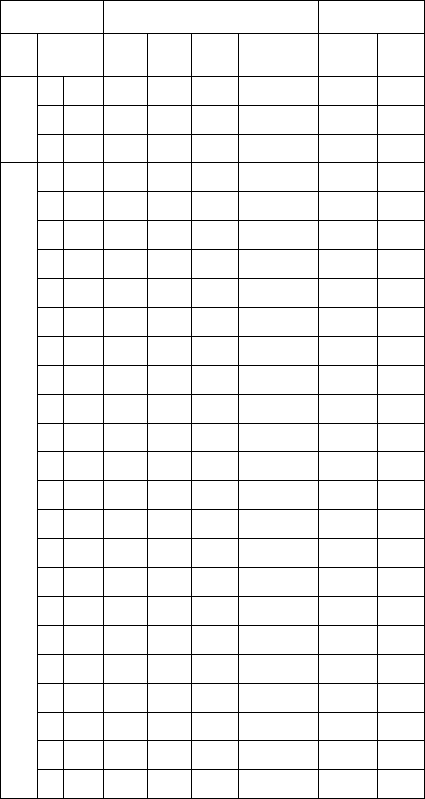
Figure 9 presents the summary of measurement
values for size and shape parameters of powder
sample identifying the variables considered in this
study. These data are used for the definition of several
models, to predict the considerable dependent
variable. These values have obtained the
consideration of 24,268, 32,302, 22,562 and 25,041
particles for Bnp, DRnp, Rnp and Ynp respectively.
For all size parameters, the value is down to 500 µm
for all powders.
The regression analysis was conducted based on
the proposed models for input systems, respectively.
The reliability of these models was compared, and the
best-fit model was identified. Table 3 displays the
corresponding R
2
values for all predictions. The
summary of models is shown in Table 3 where the
statistical coefficients analyzed are presented to
evaluate the validity of the regression model. The
model proposed for samples leads a correlation
coefficient (R) of 0.810 and a determination
coefficient (R
2
) of 0.779, thus revealing a very strong
correlation between the values predicted by the model
and the values observed in the dataset.
Table 3 shows also the analysis of variance
(ANOVA) of models. The ANOVA table reveals an
F value (Fisher-Snedecor test) of models, which is
considerably higher than the critical value of F, for a
level of significance of 5%. Moreover, the
significance value of the model is practically null,
thus lower than the p-value adopted as significance
level (5%). The results obtained reveal that all the
independent variables considered are statistically
significant in explaining the dependent variable.
As shown in Table 3, input systems led to highly
consistent R
2
values (up to 0.919) from Models 1 to 8
for predicting 𝑋
and 𝑋
, meaning similar
prediction accuracy. Model 4 (the mixed model using
size/shape as the RRV) achieved the consistently high
R
2
values for all the four predicted variables (𝑋
,
𝑋
, 𝑃𝑟
or 𝑃𝑟
).
Figure 9: Summary of measurement values for size and shape parameters of powders.
All of the corresponding R
2
values in the 25
scenarios are within the reasonable range (i.e., 0.810–
0.998). Model 1 also achieved the highest R
2
value
for the prediction of 𝑋
in both systems (0.998 for
Multi-linear regression analysis and 0.979 for Non-
linear model involving variables interactions).
In the 𝑃𝑟
or 𝑃𝑟
regression analysis, Model 6
(the non-linear approach) represents the best-fit
model by achieving even higher accuracy than others,
the highest based on both input systems.
The remaining mixed models had relatively lower
R
2
values for both input systems. The R
2
values
resulting from the best-fit non-linear and mixed
regression models in this research (ranging from
0.810–0.998) are significantly higher than the values
generated from previous studies adopting linear
methods. This can be seen in Table 3.
According to these correlation and ANOVA
coefficients, model 2, model 5 and model 6 are the
three best models to predict max distance and
geodesic length and the best model to predict
Powdering ratio index by Blaine and by LD is the
model 6 as indicated in bold in Table 3.
The linear regression coefficients (𝛼
or 𝛽
) of the
proposed models were determinate. All the
independent variables included in the model are
statistically relevant in the description of the
variability of the dependent variable, showing a
significance value lower than the p-value (5%). The
linear regression coefficients of model present a
significance value lower than the p-value (5%),
indicating that all the independent variables are
statistically relevant in the description of the
dependent response n coefficient obtained from this
test technique (Table 4). These significance values
are marked in green and the models selected on this
basis are also marked in bold in Table 4. According
to these p-values, model 2 and model 5 are the two
best models to predict max distance and geodesic
length and the best model to predict Powdering ratio
index by Blaine and by LD is the model 6 as indicated
in bold in Table 4.
Once the statistical relevance of models is
confirmed, Table 5 presents the mathematical
formulation that makes rating estimation of each
dependent response possible.
Table 3: Summary of the multiple linear regression analysis
results (In this table, *Analysis of variance of the model
(ANOVA), **Square of the mean square error (RMSE))
Parameter Correlation ANOVA*
Eq.
Model n° R R
2
R
2
ad. RMSE** F value
p
value
Equation
(
1
)
1
𝑿
𝑫𝑴
0.998 0.996 0.996 3.868045369 2436.723 0.000
2
𝑿
𝑫𝑴
0.999 0.998 0.997 2.963935818 3325.711 0.000
𝑿
𝑳𝑮
0.972 0.944 0.944 34.390131493 128.921 0.000
Equation (2)
3
𝑿
𝑫𝑴
0.942 0.888 0.866 21.326295389 40.846 0.000
𝑿
𝑳𝑮
0.959 0.919 0.904 42.540114280 58.587 0.000
𝑷𝒓
𝑺𝑩
0.951 0.904 0.885 0.286212210 48.326 0.000
𝑷𝒓
𝑺𝑳
0.945 0.892 0.871 0.244277238 42.594 0.000
4
𝑿
𝑫𝑴
0.968 0.936 0.924 16.097413373 75.576 0.000
𝑿
𝑳𝑮
0.969 0.939 0.927 36.948598108 79.335 0.000
𝑷𝒓
𝑺𝑩
0.944 0.891 0.870 0.304327341 42.150 0.000
𝑷𝒓
𝑺𝑳
0.946 0.896 0.876 0.240259398 44.204 0.000
5
𝑿
𝑫𝑴
0.989 0.979 0.974 9.349541278 234.136 0.000
𝑿
𝑳𝑮
0.980 0.960 0.952 29.887883900 123.964 0.000
𝑷𝒓
𝑺𝑩
0.942 0.888 0.866 0.308774263 40.798 0.000
𝑷𝒓
𝑺𝑳
0.944 0.892 0.871 0.244995796 42.314 0.000
6
𝑿
𝑫𝑴
0.998 0.996 0.996 3.787558166 1452.888 0.000
𝑿
𝑳𝑮
0.979 0.959 0.951 30.442169551 119.306 0.000
𝑷𝒓
𝑺𝑩
0.931 0.866 0.840 0.337897319 33.220 0.000
𝑷𝒓
𝑺𝑳
0.936 0.876 0.852 0.261645598 36.467 0.000
7
𝑿
𝑳𝑮
0.973 0.947 0.937 34.388965646 92.379 0.000
𝑷𝒓
𝑺𝑩
0.930 0.864 0.838 0.340304620 32.679 0.000
𝑷𝒓
𝑺𝑳
0.935 0.873 0.849 0.264888669 35.454 0.000
8
𝑿
𝑫𝑴
0.966 0.934 0.923 16.211425615 86.685 0.000
𝑷𝒓
𝑺𝑩
0.900 0.810 0.779 0.396643132 26.314 0.000
𝑷𝒓
𝑺𝑳
0.903 0.815 0.785 0.315815860 27.153 0.000
According to these equations with higher
correlation (Table 5), including main characteristics of
powders: the particle size, particle shape and
technological properties of powders (density, surface
area, etc.). It is demonstrated that using powders, as
well as the potential areas of their application, strongly
depends on these characteristics. Dimensionless
relationships between particle size and particle shape
can be determined theoretically for simplified, but
realistic, powder particle geometries. These
relationships have important implications for the
interpretation of shape data, and, more fundamentally,
for the selection of grain size(s) for analysis.
5 CONCLUSIONS
This study showed that the size estimation of
particulate material is a complicated matter. The
results highlight the fact that particle size
distributions may not be unique. Different techniques
can give a large range of different parameters which
need to be interpreted correctly. The choice of the
parameters also depends on the purpose of the
research. It is shown that particle shape analysis that
includes the full range of available grain sizes can
contribute not only measurements of particle size and
shape, but also information on size-dependent
densities and specific surface area.
Based on the analysis of particle characteristics,
design of experiment, and analysis of variance
(ANOVA), it can be concluded that: good correlation
was found between the specific surface area measured
by Blaine Permeability Tester and calculated from the
LD and the IA data.
Thus, based on these conclusions, it appears that
the density, specific surface area, granulometry and,
morphology of volcanic scoria powders may be
efficiently estimated from complementary
techniques. This description is absolutely needed for
understanding particles’ behavior in contact with
water when used in cementitious materials.
ACKNOWLEDGEMENTS
The first author would like to thank Mrs. Sophie
Leroy and Mr. Frédéric Michel, GeMMe research
engineers at the University of Liège (Belgium) for
their help in the testing program.
REFERENCES
Abazarpoor, A., Halali, M., Hejazi, R., Saghaeian, M.,
2017. HPGR effect on the particle size and shape of
iron ore pellet feed using response surface
methodology, Mineral Processing and Extractive
Metallurgy, pp. 1-9.
Arvaniti, E. C., Juenger, M. C. G., Bernal, S. A., Duchesne,
J., Courard, L., Leroy, S., Provis, J. L., Klemm, A., De
Belie, N., 2015a. Physical characterization methods for
supplementary cementitious materials, Materials and
Structures, 48(11):3675–3686.
Arvaniti, E. C., Juenger, M. C. G., Bernal, S. A., Duchesne,
J., Courard, L., Leroy, S., Provis, J. L., Klemm, A., De
Belie, N., 2015b. Determination of particle size,
surface area, and shape of supplementary cementitious
materials by different techniques, Materials and
Structures, 48(11):3687–3701.
Bagheri, G. H., Bonadonna, C., Manzella, I., Vonlanthen,
P., 2015. On the characterization of size and shape of
irregular particles, Powder Technology, 270:141–153.
Bouglada, M. S., Naceri, A., Baheddi, M., Pereira-de-
Oliveira, L., 2019. Characterization and modelling of
the rheological behaviour of blended cements based on
mineral additions, European Journal of Environmental
and Civil Engineering, pp. 1-18.
Bouyahyaoui, A., Cherradi, T., Abidi, M. L., Tchamdjou,
W. H. J., 2018. Characterization of particle shape and
surface properties of powders from volcanic scoria,
Journal of Materials and Environmental Science,
9(7):2032-2041.
Califice, A., Michel, F., Dislaire, G., Pirard, E., 2013.
Influence of particle shape on size distribution
measurements by 3D and 2D image analyses and laser
diffraction, Powder Technology, 237:67–75.
Dioguardi, F., Mele, D., Dellino, P., 2018. A new one-
equation model of fluid drag for irregularly shaped
particles valid over a wide range of Reynolds number,
J. of Geophysical Res.:Solid Earth, 123:144–156.
EN 196-6., 2010. Methods of testing cement - Part 6:
Determination of fineness, European Standard.
Felekoglu, B., 2009. A new approach to the
characterisation of particle shape and surface
properties of powders employed in concrete industry,
Construction and Building Materials, 23:1154–1162.
Ferraris, C. F., Hackley, V. A., Aviles, A. I., Buchanan, C.
E., 2002. Analysis of the ASTM round-Robin test on
particle size distribution of Portland cement: Phase I,
Report no. 6883. Maryland: National Institute of
Standards and Technology (NISTIR).
Gregoire, M. P., Dislaire, G., Pirard, E., 2007. Accuracy of
size distributions obtained from single particle static
digital image analysis, Proceeding. PARTEC
Conference. Nürenberg, 4p.
Hackley, V. A., Lum, L-S., Gintautas V., Ferraris, C. F.,
2004. Particle size analysis by laser diffraction
spectrometry: application to cementitious powders,
Report no. 7097. Maryland: National Institute of
Standards and Technology (NISTIR).
Ilic, M., Budak, I., Vucinic, M., Nagode, A., Kozmidis-
Luburic, U., Hodolic, J., Puskar, T., 2015. Size and
shape particle analysis by applying image analysis and
laser diffraction-inhalable dust in a dental laboratory,
Measurement, 66:109–117.
Jin, R., Chen, Q., Soboyejo, A. B. O., 2018. Non-linear and
mixed regression models in predicting sustainable
concrete strength, Construction and Building Materials,
170:142–152.
Juimo, W. H. T., Grigoletto, S., Michel, F., Courard, L.,
Cherradi, T., Abidi., M. L., 2017. Effects of various
amounts of natural pozzolans from volcanic scoria on
performance of Portland cement mortars, International
Journal of Engineering Research in Africa, 32:36-52.
Juimo, W., Cherradi, T., Abidi, L., Oliveira, L., 2016.
Characterisation of natural pozzolan of "Djoungo"
(Cameroon) as lightweight aggregate for lightweight
concrete, GEOMATE, 11(27):2782-2789.
Klemm, A. J., Wiggins, D. E., 2017. Particle size
characterisation of SCMs by mercury intrusion
porosimetry, Fizyka Budowli W Teorii I Praktyce Tom
IX, Nr 1-2017, pp 5-12.
Liu, E. J., Cashman, K. V., Rust., A. C., 2015. Optimising
shape analysis to quantify volcanic ash morphology,
GeoResJ, 8:14–30.
Michel, F., Courard, L., 2014. Particle size distribution of
limestone fillers: granulometry and specific surface
area investigations, Particulate Science and
Technology, 32:334-340.
Mikli, V., Käerdi, H., Kulu, P., Besterci, M., 2001.
Characterization of powder particle morphology,
Proceedings of the Estonian Academy of Sciences,
Engineering 7(1):22–34.
Neves, R., Silva, A., De Brito, J., Silva, R.V., 2018.
Statistical modelling of the resistance to chloride
penetration in concrete with recycled aggregates,
Construction and Building Materials, 182 : 550–560.
Niesel, K., 1973. Determination of the specific surface by
measurement of permeability, Materials and Structures,
6(3):227-231.
Orhan, M., Özer, M., Işık, N., 2004. Investigation of laser
diffraction and sedimentation methods which are used
for determination of grain size distribution of fine
grained soils, G.U. Journal of Science, 17(2):105–113.
Pavlović, M. G., Pavlović, L. J., Maksimović, V. M.,
Nikolić, N. D., Popov, K. I., 2010. Characterization
and morphology of copper powder particles as a
function of different electrolytic regimes, International
Journal of Electrochemical Science, 5:1862–187.
Slinker, B. K., Glantz, S.A., 2008. Multiple linear
regression: accounting for multiple simultaneous
determinants of a continuous dependent variable,
Circulation, 117(13):1732–1737.
Tchamdjou, W. H. J., Abidi, M. L., Cherradi, T., De
Oliveira, L. A. P., 2017a. Effect of the color of natural
pozzolan from volcanic scoria on the rheological
properties of Portland cement pastes, Energy Procedia,
139:703–709. DOI: 10.1016/j.egypro.2017.11.275.
Tchamdjou, W. H. J., Cherradi, T., Abidi, M. L., De
Oliveira, L. A. P., 2017b. Influence of different amounts
of natural pozzolan from volcanic scoria on the
rheological properties of Portland cement pastes,
Energy Procedia, 139:696–702. DOI:
10.1016/j.egypro.2017.11.274.
Varga, G., Kovács, J., Szalai, Z., Cserháti, C., Újvári, G.,
2018. Granulometric characterization of paleosols in
loess series by automated static image analysis,
Sedimentary Geology, 370, pp 1-14.

Table 4: p-value (In this table, x : non-considered variable, xx : excluded variable).
Model n° Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑿
𝑫𝑰
𝑬
𝒍
𝑿
𝑫𝑰
𝑪
𝒄
𝑿
𝑫𝑰
𝑹
𝒈
𝑾
𝒃
𝑺
𝒅
𝑾
𝒃
𝑳
𝒎
𝑾
𝒃
𝑩
𝒕
𝑿
𝑫𝑴
1 0.842 0.226 0.610 0.864 0.000 x x x x x x x x
𝐗
𝐃𝐌
2 0.121 0.001 0.304 0.107 0.000 x 0.000 x x x x x x
𝐗
𝐋𝐆
0.008 0.000 0.030 0.006 0.000 0.000 x x x x x x x
𝑋
3 0.365 x 0.120 x x x x 0.001 0.946 0.038 0.199 0.442 0.203
𝑋
0.289 x 0.046 x x x x 0.969 0.796 0.903 0.034 0.355 0.000
𝑃𝑟
0.279 x 0.405 x x x x 0.584 0.261 0.543 0.234 0.155 0.009
𝑃𝑟
0.160 x 0.287 x x x x 0.863 0.198 0.772 0.159 0.109 0.002
Model 4 Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑿
𝑫𝑨
𝑬
𝒍
𝑿
𝑫𝑨
𝑪
𝒄
𝑿
𝑫𝑨
𝑹
𝒈
𝑿
𝑫𝑨
𝑺
𝒅
𝑿
𝑫𝑨
𝑳
𝒎
𝑿
𝑫𝑨
𝑩
𝒕
𝑋
0.365 x 0.120 x x x x 0.001 0.946 0.038 0.199 0.442
0.203
𝑋
0.289 x 0.046
x x x x
0.969 0.796 0.903 0.034
0.355
0.000
𝑃𝑟
0.279 x 0.405
x x x x
0.584 0.261 0.543
0.234 0.155
0.009
𝑃𝑟
0.160 x 0.287
x x x
x 0.863 0.198 0.772 0.159 0.109 0.002
Model 5 Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑾
𝒃
𝑬
𝒍
𝑾
𝒃
𝑪
𝒄
𝑾
𝒃
𝑹
𝒈
𝑾
𝒃
𝑺
𝒅
𝑾
𝒃
𝑳
𝒎
𝑾
𝒃
𝑩
𝒕
𝑿
𝑫𝑴
0.110 x x 0.094 x x x 0.000 0.265 0.000 0.042 0.000
0.667
𝑿
𝑳𝑮
0.748 x
x 0.169 x x x 0.000 0.757 0.000 0.105 0.907
0.000
𝑃𝑟
0.334
x x
0.
605
x
x x 0.885
0.267
0.944 0.358 0.023 0.002
𝑃𝑟
0.118
x x
0.249 x x
x 0.870 0.182 0.462 0.130 0.001 0.001
Model 6 Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑳
𝒃
𝑬
𝒍
𝑳
𝒃
𝑪
𝒄
𝑳
𝒃
𝑹
𝒈
𝑳
𝒃
𝑺
𝒅
𝑳
𝒃
𝑳
𝒎
𝑳
𝒃
𝑩
𝒕
𝑋
0.519 x x x 0.966 x x 0.908 0.386 0.330 0.313 0.400
0.384
𝑋
0.783 x x
x 0.261 x x 0.001 0.952 0.084 0.185 0.336
0.000
𝑷𝒓
𝑺𝑩
0.035
x
x x 0.070 x x 0.041
0.246
0.523 0.042 0.510 0.049
𝑷𝒓
𝑺𝑳
0.012
x
x x 0.028
x x 0.091 0.183 0.533 0.017 0.260 0.017
Model 7 Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑿
𝑫𝑴
𝑬
𝒍
𝑿
𝑫𝑴
𝑪
𝒄
𝑿
𝑫𝑴
𝑹
𝒈
𝑿
𝑫𝑴
𝑺
𝒅
𝑿
𝑫𝑴
𝑳
𝒎
𝑿
𝑫𝑴
𝑩
𝒕
𝑋
0.906 x x x x 0.281 x 0.002 0.931 0.061 0.208 0.603
0.000
𝑃𝑟
0.037 x x x x 0.092 x 0.035 0.325 0.349 0.056 0.371 0.078
𝑃𝑟
0.013 x
x
x
x 0.040 x 0.078
0.255 0.352 0.023 0.176 0.030
Model 8 Const.
𝑿
𝑫𝑰
𝑿
𝑫𝑨
𝑾
𝒃
𝑳
𝒃
𝑿
𝑫𝑴
𝑿
𝑳𝑮
𝑿
𝑳𝑮
𝑬
𝒍
𝑿
𝑳𝑮
𝑪
𝒄
𝑿
𝑳𝑮
𝑹
𝒈
𝑿
𝑳𝑮
𝑺
𝒅
𝑿
𝑳𝑮
𝑳
𝒎
𝑿
𝑳𝑮
𝑩
𝒕
𝑋
0.399 x x x x x 0.076 0.010 0.111 0.136 xx 0.390
0.000
𝑃𝑟
0.182
x x
x x x 0.127
0.939 0.021
0.570 xx 0.499
0.000
𝑃𝑟
0.122 x
x
x x
x
0.160 0.585
0.011 0.460 xx 0.351 0.000
Table 5: Equations of efficient models identified.
Model n° Equations R
2
Model 2
X
1.167 0.435X
0.281X
0.501
W
1.043L
0.056X
0.998
X
22.528 6.003X
6.718X
9.542
W
8.240L
7.590X
0.944
Model 5
X
6.306 4.455
W
1.989
W
E
0.827
W
C
4.877
W
R
5.815
W
S
1.377
W
L
0.157
W
B
0.979
X
3.989 11.619
W
6.019
W
E
0.727
W
C
8.110
W
R
14.650
W
S
0.053
W
L
7.069
W
B
0.960
Model 6
Pr
0.302 0.145L
0.031L
E
0.024L
C
0.025L
R
0.175L
S
0.006L
L
0.021L
B
0.866
Pr
0.282 0.137L
0.019L
E
0.021L
C
0.019L
R
0.162L
S
0.008L
L
0.020L
B
0.876
