Predicting Covid-19 Cases using CNN Model

Paul Menounga Mbilong

, Asmae El Kassiri

, Fatima-Zahra Belouadha

and El Bhiri Brahim

AMIPS Research Team, Ecole Mohammadia d’Ingénieurs, Mohammed V University in Rabat

SMARTLIB, Ecole Marocaine des Sciences de l'Ingénieur Rabat, Morocco

Keywords: The COVID-19, CNN, LSTM, Deep Learning, Time-series forecasting.

Abstract: The prediction of COVD-19 confirmed cases is a complex time-series problem. In the literature, Long Short

Time Memory (LSTM) has proven its efficiency to resolve issues related to the time series problems. However,

Convolution neural network (CNN) did not been widely used in this aim and is considered as more suitable

for imaging processing. Therefore, in this paper, we use it to predict COVID-19 cases and compared it with

LSTM in the context of Morocco during the period of confinement. The obtained results which we present

and discuss in this article are very promising.

1 INTRODUCTION

Reported first in December 2019, in Wuhan, China,

Coronavirus 2019 (COVID-19), caused by the strain

of coronavirus named “Severe Acute Respiratory

Syndrome Coronavirus 2 (SARS-CoV-2)”, has

become now, according to the World Health

Organization WHO, an international epidemic having

caused 17 660 523 infected cases, and 680 894 deaths

on August 03, 2020 (Organization, 2020).

Since the first cases were reported, multiple

academic and medical works have explored various

approaches to find a solution for the COVID-19

epidemic in different search areas including the

Machine Learning (ML). Some ML, and especially

Deep Learning (DL), work interested in COVID-19

are oriented to help medical staff to efficiently

diagnostic infected people (Singh, Kumar, Vaishali,

& Kaur, Coronavirus (COVID-19) Classification

using CT Images by Machine Learning Methods,

2020) (Wang, et al., 2020) (Gozes, et al., 2020)

(Metsky, Freije, Kosoko-Thoroddsen, & Myhrvold,

2020), and others are directed to analyze the

pandemic situation like predicting new patients to

contribute to local hospital arrangement (Alimadadi,

et al., 2020) (Bouhamed, 2020) (Chimmula & Zhang,

2020) (Pinter, Felde, MOSAVI, Ghamisi, &

Gloaguen, 2020).

In general, a lot of work applied ML and DL to

predict COVID-19 new cases use time-series

https://orcid.org/0000-0001-5464-4803

forecasting models (Chimmula & Zhang, 2020)

(Zeroual, Harrou, Dairid, & Sun, 2020) (Azarafza,

Azarafza, & Tanha, 2020) (Punn, Sonbhadra, &

Agarwal, 2020). Actually, Recurrent Neural

Networks (RNN) architecture are adopted by several

searchers thanks to their capacity in handling time-

dependent datasets, and hence they were widely used

in the context of predicting COVID-19 new cases.

Moreover, other Neural Networks (NN) architectures

were used for this objective.

The objective of this work is to use Convolution

Neural Network (CNN) architecture in time-series

forecasting to predict the COVID-19 new cases in

Morocco. We compare our results with a Long Short-

Term Memory (LSTM) neural network explored in

the same context by another work conducted by our

research team.

This paper is constituted of five sections. The

second one explores the related work, which is

relative to CNN architectures and their use in Time-

series forecasting, especially in the context of

COVID-19. The third section is about Materials and

Method used to perform our experimental studies. We

present and discuss the results in the fourth section,

and finally we conclude in the fifth section.

2 RELATED WORK

Most often, a time-series is a succession of points

equidistant in time. It can be thought of as sequence

of vectors s(t), with t between 0 to n, where t denotes

the spent time, x is a value varying with t, and n is the

max value of t. The problem of forecasting future

values of s from values of s up to the current time can

be stated as finding a function f : ℝ



→ ℝ such as to

estimate s at time t + d, from the N time steps back

from time t (Frank, Davey, & Hunt, 2001):

s (t + d) = f(s(t), s (t − 1), . . ., s (t − N + 1)) (1)

In the literature, RNN architectures were

considered the most suitable for solving problems that

involve sequential data (Ganatra & Patel, 2018).

LSTM is a special type of recurrent neural

network with long and short term memory cells

(Kamal, Bae, Sunghyun, & Yun, 2020). It was proven

that it has good accuracy in the context of COVID-19

prediction. In (Azarafza, Azarafza, & Tanha, 2020),

LSTM was more efficient than RNN in predicting

infections in Iran, while LSTM learning has given

good RMSE and suggested that the epidemic's

expected outcome will be reached in the period of

June 2020 in (Chimmula & Zhang, 2020) but the

actual situation proves that it was not true. We think

it is because of the small size of the analyzed data set

(confirmed cases until March 31, 2020).

Nevertheless, comparing LSTM, RNN, GRU, and

Variational AutoEncoder VAE have proven the

efficiency of VAE (Zeroual, Harrou, Dairid, & Sun,

2020).

The CNN architectures as shown in Figure 1, in

the other side, were basically designed to extract local

relationships that are invariant across spatial

dimensions. Commonly they have three types of

layers; including fully-connected layer, pooling layer,

convolutional and non-linearity layers (Abiodunab, et

al., 2018).

Figure 1: An example of CNN architecture (Hidaka &

Kurita, 2017).

To adapt CNNs to time-series datasets,

researchers use multiple layers of causal convolutions

(Oord, et al., 2016) (Bai, Kolter, & Koltun, 2018).

For an intermediate feature at hidden layer l, each

causal convolutional filter takes the form below (Lim

& Zohren, 20):

ℎ







𝐴

𝑊 ∗ ℎ𝑙,𝑡

(2)



𝑊∗ℎ



𝑙,𝑡



𝑤𝑙,𝜏ℎ









(3)

where ℎ





∈ ℝ





is an intermediate state at

layer l at time t, ∗ is the convolution operator, W(l, τ

) ∈ ℝ









is a fixed filter weight at layer l, and

A(.) is an activation function representing any

architecture-specific non- processing. In practice, the

one-dimensional 1-D CNN architecture is used to

classify and predict future time-series values.

In the context of COVID-19 analysis, the CNN

architectures were widely used to detect it from X-ray

or Computed Tomography CT images. On the X-ray

images side, authors in (Apostolopoulos & Mpesiana,

2020) utilized a dataset of X-beam pictures from

patients with regular bacterial pneumonia, affirmed

Covid-19 sickness, and ordinary occurrences to

distinguish the COVID-19 infection. Similarly, in

(Ozturk, et al., 2020), the authors use a dataset of raw

chest X-ray images with the DarkNet model (based

on CNN architecture) to give exact diagnostics,

classify people with the COVID for those who don't

have the COVID-19 and for multi-class classification

between COVID contaminated people, healthy

individuals and persons with pneumonia. Authors in

(Minaee, Kafieh, Sonka, Yazdani, & Soufie, 2020)

used a transfer learning on a subset of 2000 x-ray

images to learn four successful CNNs models ,

comprising ResNet18, ResNet50, SqueezeNet, and

DenseNet-121, to recognize COVID-19 illness in a

chest image dataset collected from the publicly

available datasets, and images exhibiting COVID-19

disease presence were identified by board-certified

radiologist. While authors in (Islam & Asraf, 2020)

use a dataset of 4575 X-ray images, including 1525

images of COVID-19, the CNN to extract for deep

feature and LSTM to detect COVID-19 using the

extracted feature. On the other side, authors (Singh,

Kumar, Vaishali, & Kaur, Classification of COVID-

19 patients from chest CT images using multi-

objective differential evolution–based convolutional

neural networks, 2020) use a dataset of chest CT

images and a CNN model to assign COVID-19

infected patients as infected and uninfected in another

case. They calibrated the settings of CNN based on

the multi-objective differential evolution. Similarly,

authors in (Wang, et al., 2020) use a dataset of 1,065

CT images of pathogen-confirmed COVID-19 cases

(325 images) along with those previously diagnosed

with typical viral pneumonia (740 images) and a

transfer-learning model to train a CNN model

followed by an internal and an external validation.

The CNN did not have the same popularity in the

context of time-series forecasting of COVID-19

cases. Up to day, there are only four works that have

exploited the CNN architectures to predict COVID-

19, in the literature. The first one is (Amo-Boateng,

2020) where 1D-CNN is used on the chronological

data records of known COVID-19 positive cases in

order to predict the steps for reporting countries and

territories. The second one is (Barman, 2020) that

explores the performance of Auto-Regressive

Integrated Moving Average (ARIMA) model and

several LSTM models, including the CNN-LSTM, in

forecasting the number of confirmed COVID-19

cases. According to the authors, ARIMA marked

better results. The third one is (Dutta,

Bandyopadhyay, & Kim, 2020) a study that

investigates the forecast of the growth of COVID-19

at a close later time in the world through the CNN and

CNN-LSTM models. The results demonstrate that the

mixed CNN-LSTM framework is more efficient than

the rest of the models. The last one is (Huang, Chen,

Ma, & Kuo, 2020) that proposes a CNN model to

analysed and predict the number of confirmed cases

in several cities with the most confirmed cases in

China. The findings of the research stated that, in

comparison to a number of alternative deep learning

methods (Multilayer perceptron (MLP), LSTM, and

Gate Recurrent Unit (GRU)), the CNN model

proposed in this study is promising.

As seen in the previous works, to predict COVID-

19 cases, some works pretend that LSTM fits better

than CNN, while others pretend the contrary. In this

present work, we will use the CNN model in this

context and compare our results with another

submitted work investigating the efficiency of LSTM

for the same objective on the same dataset.

3 MATERIALS AND METHODS

The approach consists in three principle tasks. The

first one is a data pre-processing to prepare data to be

analysed. The second, the third and the last one,

respectively, are the model parametrization, training

and testing. Those tasks are recursive according to the

evaluation metrics until finding the best-fitted model.

The retained model is then used for the prediction.

3.1 Data Set

This For our study, we have decided to explore data

from Our World in Data that uses three statistical

resources on the COVID-19 pandemic published by

the European Center for Disease Prevention and

Control (ECDC). The dataset contains aggregated

data from countries around the world that are

available on GitHub. The variables represent data

related to confirmed cases, deaths, and testing, as well

as other variables of potential interest. The columns

are: iso code, continent, location, date, total cases,

new cases, total deaths, new deaths, total cases per

million, new cases per million, total deaths per

million, new deaths per million, total tests, new tests,

new tests smoothed, total tests per thousand, new tests

per thousand, new tests smoothed per thousand, tests

units, stringency index, population, population

density, median age, aged 65 older, aged 70 older,

gdp per capital, extreme poverty, cardiovascular

death rate, diabetes prevalence, female smokers, male

smokers, handwashing facilities, hospital beds per

thousand, life expectancy. Note that the analysed data

belong to the period from March 02, 2020 to June 15,

2020.

3.2 Pre-processing

The collected data were then processed by a Python

project using the libraries Pandas, NumPy, SciPy and

Matplotlib in a jupyter notebook.

We have first filtered data concerning Morocco,

and then selected the features 'total_cases',

'population', 'total_deaths', and 'new_deaths. We have

retained the last feature ‘new_cases’ because it is the

target of our predictions. The features concerning the

total of deaths and cases are useful for the prediction

because the contamination can arise from infected

people that are always alive.

The third task was the feature scaling to normalize

the range of independent variables or features of data

so that each feature contributes approximately and

proportionately in the ML algorithm. We have then

applied the Min-Max scaler that transforms all values

between the range 0 and 1. The fourth task of the pre-

processing process is adapting our model to learn

from the past time-steps in order to predict the positive

COVID-19 cases for the future 7 time-steps, where we

split the dataset into 80% of the training set and 20%

of the testing set. The model uses two days lags as

inputs to predict seven days as outputs.

3.3 Parameters

The choice of the activation function, the optimizer,

and the number of layers were fixed at the beginning,

while the number of filters in the CNN layers were

updated recursively according to the evaluation steps

to enhance the performance of the trained model. The

best performance was obtained by 127 filters. The

amount of days to return by the model depends on the

number of outputs in last layer, in our paper, that is

set to 7.

In this work, we have opted for the activation

function ReLu and the Adam Optimizer belonging to

the stochastic gradient descent SGD category.

In a neural network, the activation function takes

in the output signal from the previous cell and

converts it into some form that can be taken as input

to the next cell. Similarly, in an artificial neural

network (ANN), it transforms the summed weighted

input from the node into the output for that input. The

rectified linear activation function ReLU is a linear

function that outputs the input directly if it is positive,

otherwise, it will output zero. It is especially when

using CNN, a widely used activation function and

easy to compute which does not saturate, and prevents

the Vanishing Gradient Problem.

The optimizer is a basic algorithm responsible for

making neural networks converge, it controls the

weights updating of the network, to shift towards the

optimum of the cost function. On the basis of this, we

have two basic types of gradient descent algorithms.

The BGD, batch gradient descent and the SGD,

stochastic gradient descent. The main distinction

between the both is that the SGD will compute the

cost of only one example in each step, when the BGD

will determine the cost of all the training instances in

the dataset.

The SGD formula is employed to adjust the

weights in a neural network through the use

backpropagation to calculate the gradient ∇ Hansen,

2019:

𝜃



𝜃





.∇



𝐽𝜃;𝑥,𝑦













(4)

- θ (theta) is the variable to be modified during

the optimization of a model, it can be weights,

biases and activations. Notice that a single

weight is updated for the neural network here,

- η is the learning rate (eta),

- ∇ is the gradient (nabla),

- J has formally been known as an objective

function, but most often it is called a cost

function or loss function.

- J (θ; x, y) basically implies that we insert the θ

parameter along with a training example and

label.

Adaptive Moment Estimation (Adam) is the most

frequently used optimizer and certainly the top

performer on general average.

3.4 Evaluation Metrics

MSE (Mean Square Error). It is used as a default

metric for evaluation of the performance of most

regression algorithms (Kathuria, 2019). It computes

the average of the squared errors, defined as the mean

difference between the real values y and the estimated

y (Binieli, 2018). A large MSE means a large error.

RMSE (Root Mean Square Error) has been used

as a standard statistical metric to measure model

performance in meteorology, air quality, and climate

research studies (Chai & Draxler, 2014). It

corresponds to the square root of the mean of the

squared difference between the observed y and the

predicted values y (Bratsas, et al., 2020).

Max Error is a metric which calculates the

maximum residual error. It expresses the worst case

error between the predicted value and the true value.

Its interpretation is very simple.

R2 (R-Square) is a metric that varies between 0

and 1. It is also known as the Coefficient of

Determination. Sometimes, the closer to 1 it is, the

better the model is (Vedova, 2018).

MAE (Mean Absolute Error) is the averaged on

the test instance for absolute differences between the

forecast and the true observation where all individual

errors were given the same weight.

3.5 1D-CNN Architecture

The 1D-CNN structure proposed in this study is

illustrated in Figure 2 The design of the input layer

uses two-time sequences that are based on factors

influencing the number of new cases. The structure of

the convolutional layer contains a single layer with

127 filters.

Figure 2: Structure of proposed CNN model.

The convolution process can be expressed in

Equation (5). Let call f our input vector and g our

filter, and say that f has length n, and g has length m.

The convolution f ∗ g of f and g is defined as:



 σ  w



 ⋯ w





(5)

The idea behind the fully connected layer

architecture can be formulated by equation (5). Let x

∈ ℝ

represent the input to a fully connected layer.

Let y

∈ ℝ be the i-th output from the fully connected

layer. Then y

∈ ℝ is computed as follows:

𝑥







∗g



i 

∑

g𝑖 ∗

i  j 











(6)

Here, σ is a nonlinear function (in this case is

ReLu), and the w

are learnable weights (thanks to the

optimizer) in the network. The result of the

convolution layer can generate a 1D vector through

flattened technique. Then the vectors are plugged into

the fully connected (dense) layer to obtain a 1D vector

output.

4 RESULTS AND DISCUSSION

In this section, we compare and discuss the results of

the proposed CNN model and the best-fitted LSTM

model developed by our research team. The two

models were trained and tested on the same dataset.

Table 1 shows the evaluations from the proposed

CNN using the MSE, RMSE, MAE, R2, and

MaxError metrics. As seen, the model converges well

to a small error of the training loss with an MSE of

267.23, an RMSE of 16.35, an MAE of 11.74, and an

R2 of 0.68. Actually, the model continues to well

converge to a small error in the test stage with an

MSE of 723.95, an RMSE of 26.91, an MAE of

20.06, and an R2 of 0.15.

Table 2 shows the experiment results of the best-

fitted model among the LSTM ones that our research

team has developed. It shows that the LSTM model

converges slightly better than the proposed CNN

model, in the test stage with an MSE of 658.65, an

RMSE of 25.66, an MAE of 19.95, and an R2 of 0.23.

Taking into consideration that the best-fitted LSTM

model implements three LSTM layers, while the

proposed CNN model implements only one CNN

layer. It must be admitted that the proposed model is

very promising.

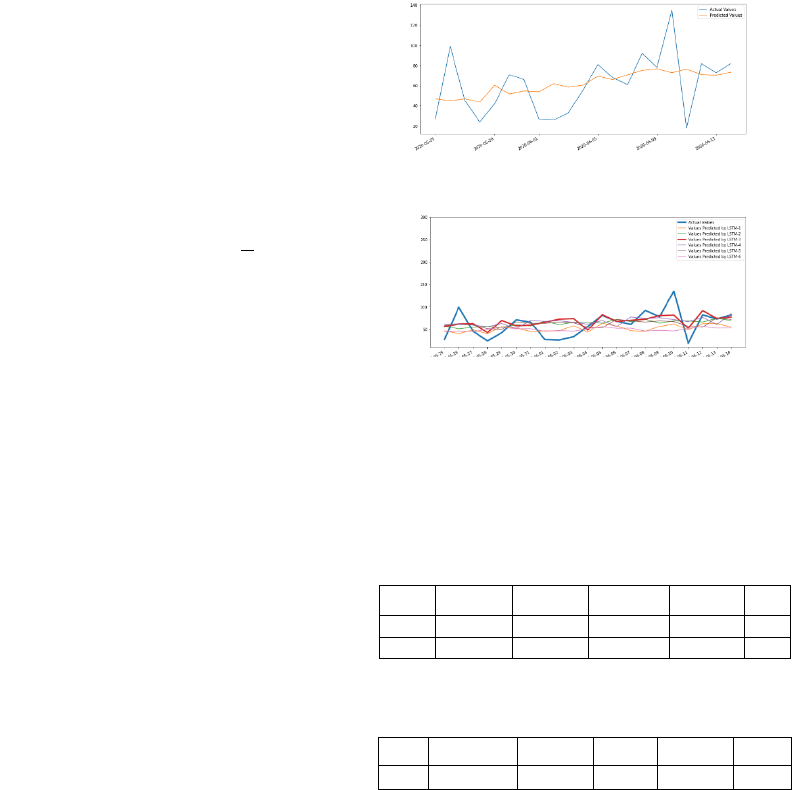
Figure 3:Curve of the CNN test.

Figure 4:Test curves from research team LSTM models.

Examining these curves for the purpose of the

comparison between real values and predicted values

using the proposed CNN model (Figure 3) and the

LSTM model (red one on Figure 4), we can notice

that the two models are very close.

Table 1: Evaluation of the proposed CNN model.

Model MSE RMSE MAE R2

Train CNN 267.23 16.35 11.74 0.68

Test CNN 723.95 26.91 20.06 0.15

Table 2: Test results of our research team best-fitted LSTM

model.

Model MSE RMSE MAE R2

Test

LSTM-3 658.65 25.66 19.95 0.23

5 CONCLUSIONS

In this work, we explore the efficiency of CNN model

to predict new cases in Morocco using a dataset of

time series data from March 02, 2020 to June 15,

2020. The experiments showed that a CNN model

with a single CNN layer is almost as efficient as an

LSTM model with three LSTM layers. It allows a

good prediction accuracy with an RMSE of 26.91.

Our findings and conclusions are demonstrated and

enhanced by various illustrations we provide in this

paper.

The results of the proposed CNN are very

promising and show that CNN can be a potentially

good alternative to LSTM model for similar problem.

This indeed encourages exploring its efficiency with

other settings such as more layers and more features.

ACKNOWLEDGEMENTS

This paper was written within the scope of a COVID-

19 project supported by the supervisory ministry

MENFPESRS and the CNRST of Morocco with the

aim of prevention and forecast the spread of the

COVID-19 pandemic.

REFERENCES

Abiodunab, O. I., Jantana, A., Omolarac, A. E., Dadad, K.

V., Mohamede, N. A., & Arshad, H. (2018). State-of-

the-art in artificial neural network applications: A

survey. Heliyon, 4(11), No e00938.

Alimadadi, A., Aryal, S., Manandhar, I., Munroe, P. B., Joe,

B., & Cheng, X. (2020). AI and Machine Learning for

Understanding Biological Processes. Physiological

Genomics, 52(4), 200-202.

Amo-Boateng, M. (2020). Tracking and Classifying Global

COVID-19 Cases by using 1D Deep Convolution

Neural Network. medRxiv, No 2020.06.09.20126565.

Apostolopoulos, I. D., & Mpesiana, T. A. (2020). Covid-19:

automatic detection from X-ray images utilizing

transfer learning with convolutional neural networks.

Physical and Engineering Sciences in Medicine, 43,

635–640.

Azarafza, M., Azarafza, M., & Tanha, J. (2020). COVID-

19 Infection Forecasting based on Deep Learning in

Iran. medRxiv.

doi:https://doi.org/10.1101/2020.05.16.20104182

Bai, S., Kolter, J. Z., & Koltun, V. (2018). An Empirical

Evaluation of Generic Convolutional and Recurrent

Networks for Sequence Modeling. arXiv, No

arXiv:1803.01271 .

Barman, A. (2020). Time Series Analysis and Forecasting

of COVID-19 Cases Using LSTM and ARIMA

Models. arXiv, No 2006.13852.

Binieli, M. (2018, 10 16). Machine learning: an

introduction to mean squared error and regression

lines. Retrieved 08 02, 2020, from

https://www.freecodecamp.org/news/machine-

learning-mean-squared-error-regression-line-

c7dde9a26b93/

Bouhamed, H. (2020). Covid-19 Cases and Recovery

Previsions with Deep Learning Nested Sequence

Prediction Models with Long Short-Term Memory

(LSTM) Architecture. International Journal of

Scientific Research in Computer Science and

Engineering, 8(2), 10-15.

Bratsas, C., Koupidis, K., Grau, J. M., Giannakopoulos, K.,

Kaloudis, A., & Aifadopoulou, G. (2020). A

Comparison of Machine Learning Methods for the

Prediction of Traffic Speed in Urban Places.

Sustainability , 12(1), No 142.

Chai, T., & Draxler, R. R. (2014). Root mean square error

(RMSE) or mean absolute error (MAE)? – Arguments

against avoiding RMSE in the literature. Geoscientific

Model Development, 7(3), 1247-1250.

Chimmula, V. K., & Zhang, L. (2020). Time series

forecasting of COVID-19 transmission in Canada using

LSTM networks. Chaos Solitons Fractals, 135, No

109864.

Dutta, S., Bandyopadhyay, S., & Kim, T.-H. (2020). CNN-

LSTM Model for Verifying Predictions of Covid-19

Cases. Asian Journal of Computer Science and

Information Technology, 5(4), 25-32.

Frank, R. J., Davey, N., & Hunt, S. P. (2001). Time Series

Prediction and Neural Networks. Journal of Intelligent

and Robotic Systems, 31, 91–103.

Ganatra, N., & Patel, A. (2018). A Comprehensive Study of

Deep Learning Architectures, Applications and Tools.

INTERNATIONAL JOURNAL OF COMPUTER

SCIENCES AND ENGINEERING, 6(12), 701-705.

Gozes, O., Frid-Adar, M., Greenspan, H., Browning, P.,

Zhang, H., Ji, W., . . . Siegel, E. (2020). Rapid AI

Development Cycle for the Coronavirus (COVID-19)

Pandemic: Initial Results for Automated Detection &

Patient Monitoring using Deep Learning CT Image

Analysis. arXiv, No arXiv2003.05037.

Hansen, C. (2019, 10 16). Optimizers Explained - Adam,

Momentum and Stochastic Gradient Descent. Retrieved

08 25, 2020, from

https://mlfromscratch.com/optimizers-explained/#/

Hidaka, A., & Kurita, T. (2017). Consecutive

Dimensionality Reduction by Canonical Correlation

Analysis for Visualization of Convolutional Neural

Networks. Proceedings of the ISCIE International

Symposium on Stochastic Systems Theory and its

Applications, 160-167.

Huang, C.-J., Chen, Y.-H., Ma, Y., & Kuo, P.-H. (2020).

Multiple-Input Deep Convolutional Neural Network

Model for COVID-19 Forecasting in China. medRxiv,

https://doi.org/10.1101/2020.03.23.20041608.

Islam, M. Z., & Asraf, A. (2020). A combined deep CNN-

LSTM network for the detection of novel coronavirus

(COVID-19) using X-ray images. Informatics in

Medicine Unlocked, 20, No 100412.

Kamal, I. M., Bae, H., Sunghyun, S., & Yun, H. (2020).

DERN: Deep Ensemble Learning Model for Short- and

Long-Term Prediction of Baltic Dry Index. Applied

Sciences, 10(4), No 1504.

Kathuria, C. (2019, 12 5). Regression — Why Mean Square

Error? Retrieved 08 02, 2020, from

https://towardsdatascience.com/https-medium-com-

chayankathuria-regression-why-mean-square-error-

a8cad2a1c96f

Lim, B., & Zohren, S. (20). Time Series Forecasting With

Deep Learning: A Survey. arXiv, No

arXiv:2004.13408.

Metsky, H., Freije, C., Kosoko-Thoroddsen, T.-S. S., &

Myhrvold, C. (2020). CRISPR-based COVID-19

surveillance using a genomically-comprehensive

machine learning approach. bioRxiv, No

bioRxiv2020.02.26.967026.

Minaee, S., Kafieh, R., Sonka, M., Yazdani, S., & Soufie,

G. J. (2020). Deep-COVID: Predicting COVID-19

from chest X-ray images using deep transfer learning.

Medical Image Analysis, 65, No 101794.

Oord, A. v., Dieleman, S., Zen, H., Simonyan, K., Vinyals,

O., Graves, A., . . . Kavukcuoglu, K. (2016). WaveNet:

A Generative Model for Raw Audio. arXiv, No

arXiv:1609.03499.

Organization, W. H. (2020, 08 02). Coronavirus disease

Situation Report – 138. Retrieved 08 03, 2020, from

https://www.who.int/docs/default-

source/coronaviruse/situation-reports/20200606-covid-

19-sitrep-138.pdf?sfvrsn=c8abfb17_4

Ozturk, T., Talo, M., Yildirim, E. A., Baloglu, U. B.,

Yildirime, O., & Acharya, U. (2020). Automated

detection of COVID-19 cases using deep neural

networks with X-ray images. Computers in Biology and

Medicine, 121, No 103792.

Pinter, G., Felde, I., MOSAVI, A., Ghamisi, P., &

Gloaguen, R. (2020). COVID-19 Pandemic Prediction

for Hungary; a Hybrid Machine Learning Approach.

medRxiv: The preprint Server for Health Sciences,

medRxiv 2020.05.02.20088427.

doi:https://doi.org/10.1101/2020.05.02.20088427

Punn, N. S., Sonbhadra, S. K., & Agarwal, S. (2020).

COVID-19 Epidemic Analysis using Machine Learning

and Deep Learning Algorithms. medRxiv, No medRxiv

2020.04.08.20057679.

Singh, D., Kumar, V., Vaishali, & Kaur, M. (2020).

Classification of COVID-19 patients from chest CT

images using multi-objective differential evolution–

based convolutional neural networks. European

Journal of Clinical Microbiology & Infectious Diseases

, 39, 1379–1389.

Singh, D., Kumar, V., Vaishali, & Kaur, M. (2020).

Coronavirus (COVID-19) Classification using CT

Images by Machine Learning Methods. European

Journal of Clinical Microbiology & Infectious

Diseases, 39, 1379–1389.

doi:https://doi.org/10.1007/s10096-020-03901-z

Vedova, C. D. (2018, 07 31). Régression linéaire simple :

le R2, info ou intox ? Retrieved 08 02, 2020, from

https://statistique-et-logiciel-r.com/regression-lineaire-

simple-le-r%C2%B2-info-ou-intox/

Wang, S., Kang, B., Ma, J., Zeng, X., Xiao, M., Guo, J., . .

. Xu, B. (2020). A deep learning algorithm using CT

images to screen for Corona Virus Disease (COVID-

19). medRxiv,

https://doi.org/10.1101/2020.02.14.20023028.

Wang, Y., Hu, M., Li, Q., Zhang, X.-P., Zhai, G., & Yao,

N. (2020). Abnormal respiratory patterns classifier may

contribute to large-scale screening of people infected

with COVID-19 in an accurate and unobtrusive

manner. arXiv, No arXiv2002.05534.

Zeroual, A., Harrou, F., Dairid, A., & Sun, Y. (2020). Deep

learning methods for forecasting COVID-19 time-

Series data: A Comparative study. Chaos, Solitons &

Fractals, 140, No. 110121.