The Optimized Geometry Solar Chimney as Passive Cooling Solution

for Buildings in Jakarta

Dalhar Susanto and M. Aryo Wicaksono

Department of Architecture, Faculty of Engineering, Universitas Indonesia, Kampus UI Street, Kukusan, Depok, Indonesia

Keywords: Geometry solar-chimney, Passive-cooling, Ventilation.

Abstract: Solar chimney uses solar radiation to trigger the buoyancy-driven flow in the building to allow saturated air

inside the building to flow out of the building. At this stage, this research aims to find the optimized geometry

for the solar chimney that can be used in Jakarta and display the performance of the optimized solar chimney

as one of the solutions for passive cooling. In the present paper, the numerical method investigates the airflow,

temperature distribution, and thermal comfort inside the empty room without any human and mechanical

activity connected with an inclined solar chimney. RNG k-epsilon modeled the steady-state 3D computational

fluid dynamics (CFD) to investigate flow inside the chimney. Discrete ordinate (DO) non-grey radiation

model with solar ray tracing is used to simulate heat transfer in the chimney from each time in Jakarta.

Chimney geometry parameters were monitored from inclination angle, width, air gap, chimney length,

airflow, and average outlet velocity. This research's result is that the optimized solar chimney's optimized

geometry is suitable for Jakarta climate and the optimized solar chimney's performance as passive cooling in

Jakarta.

1 INTRODUCTION

Air conditioning or ventilation purposes use the

most energy demand in a building. Space

cooling dominates half of the energy demand in

commercial buildings, followed by lighting,

cooking, and water heating. Nowadays, people

tend to use mechanical air conditioning or

ventilation to achieve thermal comfort in the

building. Mostly, non-renewable energy is used

to generate electricity to power this mechanical

ventilation.

Solar chimney uses solar radiation to trigger the

buoyancy-driven flow in the building to allow

saturated air inside the building to flow out of the

building. At this stage, this research aims to find the

optimized geometry for the solar chimney that can be

used in Jakarta and display the performance of the

optimized solar chimney as one of the solutions for

passive cooling. In the present paper, the numerical

method investigates the airflow, temperature

distribution, and thermal comfort inside the empty

room without any human and mechanical activity

connected with an inclined solar chimney. In this

research, ANSYS FLUENT 2020 R2 Academic was

employed to develop a three-dimensional numerical

model for this research.

2 RESULTS AND DISCUSSION

2.1 Model

The model is based on research that was done by

abdeen et al (Abdeen, et al., 2019). A wooden

chamber with 3 m x 3 m x 3 m connected to the

chimney on the ceiling and the absorber facing the

north, opening measured 0,6 m x 0,6 m on the south

side of the room. For the simulation's initial stage, the

chimney is measured with 1,4 m lengths, inclined to

, 0,6 m width, 0,25 m air gap—this model is

located in jakarta with coordinate 6.21462

106.84513

e. The chimney's geometry, such as

length, inclination angle, width, and air gap, will be

varied at the later stage of this simulation using the

design exploration feature in ansys.

Susanto, D. and Wicaksono, M.

The Optimized Geometry Solar Chimney as Passive Cooling Solution for Buildings in Jakarta.

DOI: 10.5220/0010792200003317

In Proceedings of the 2nd International Conference on Science, Technology, and Environment (ICoSTE 2020) - Green Technology and Science to Face a New Century, pages 53-57

ISBN: 978-989-758-545-6

Figure 1. Ventilation flow diagram of the model

The chimney itself is made of 4 mm clear glass on the

north, 4 mm opaque glass on the west and east side of

the chimney, 1 mm steel sheet on the south side of the

chimney act as absorber, and 50 mm insulation glass

wool on the backside of the absorber to prevent heat

loss from the absorber.

2.2 Mesh

The hexahedral mesh was implemented in this model,

with a total of mesh 112.175 elements. If the mesh

number is lower than the current total mesh, the

simulation will fail in some chimney variation models

using the Design Exploration feature. If more

extensive, the simulation's runtime will be longer, but

the results will be more accurate.

Figure 2. The meshing of the model

2.3 Computational Fluid Dynamics

Configuration

Three-dimensional, fully turbulent, and

incompressible flow is conducted with ANSYS

FLUENT. The energy model is set to activate to

simulate the heat transfer of the chimney. The

renormalization group (RNG) k-ε model is

implemented to simulate chimney flow. This model

is the most accurate in flow separation, streamline

curvature, and flow stagnation (Chen, 1995).

Gravitation at Y-axis is set to 9,8 m/s2. The buoyancy

effect is activated. For wall setting, the standard

treatment is implemented for this simulation.

Figure 3. Model setup for flow

The discrete ordinate (DO) model is implemented to

simulate the solar load model's radiation to the

chimney. The setup for the solar load model in this

simulation is placed in Jakarta. The solar load model

is set to 11:00 on 1 August because between June to

August is when demand for ventilation is high in a

year.

Figure 4. Model setup for radiation

ICoSTE 2020 - the International Conference on Science, Technology, and Environment (ICoSTE)

Figure 5. Solar calculator setup

Thermo-physical for fluid properties is assumed

to be constant except density. Density is modeled by

the Boussinesq approximation, which delivers faster

convergence than models that vary density as a

function of temperature (ANSYS Fluent. co, 2015).

Thermo-physical properties for other materials, such

as glass, steel, wood, and insulation, based on Table

Table 1. Material setup for model

Properties Air Glass Steel Wood

Insu

lation

Density

(kg/m

)

Bous

sines

q =

1,18

2220 8030 700 10

(Speciﬁc

Heat)

(J/(kg K))

1006.

830

502,4

2310 830

Thermal

Conductivit

y (W/(m

K))

0,024

1,15 16,27 0,173 0,1

Viscosity

(kg/(m s))

1,789

4*10

−

- - - -

Thermal

Expansion

Coeﬃcient

(1/K)

0,003

- - - -

The Semi-Implicit Method for Pressure-Linked

Equations (SIMPLE) algorithm was applied as

pressure-velocity coupling. The least-square cell-

based method is applied as a gradient discretization.

The staggering pressure option (PRESTO!) method is

applied as pressure discretization. The second-order

upwind method is applied for momentum, turbulent

kinetic energy, turbulent dissipation rate, energy, and

discrete ordinates discretization. Absolute

convergence is achieved when residuals were less

than 10

-4

For boundary conditions, a no-slip condition is

applied for every wall in the model. Mixed thermal

conditions were applied for all heated surfaces. The

ambient temperature and pressure were assumed to be

C and 1 atm. A pressure inlet with zero-gauge

pressure is set as a room inlet with incoming air

assumed to be equal to ambient temperature. A

pressure outlet with zero-gauge pressure is set to be a

room outlet assumed to be equal to the ambient

pressure.

2.4 Design Optimization

Chimney geometry, such as length, inclination angle,

width, and air gap, will be varied until the outlet

achieves optimized airflow and velocity. Using CFD

to simulate each variable will be a long process. To

shorten the process for each variation and optimize

the output, ANSYS 2020 R2 Design Exploration is

employed.

Figure 6. Design Exploration steps in ANSYS

The process for optimization encompasses the

initial sampling step through Design of Experiments

(DOEs), followed by interpolation technique using

Response Surface Method (RSM) and optimization

using the Multi-Objective Genetic Algorithm

(MOGA).

2.4.1 Design of Experiments (DOEs)

The large number of tests required for one-by-one

parameter variation will be time-consuming and not

efficient. Although this step is also time-consuming,

this process is more efficient than many tests. DOEs

is a statistical approach that explores interactions

between design and output variables through

minimum sampling points, which is set to 25

sampling points in this research. Angle, width,

inclination angle, and air gap are stated as input

parameters, then airflow and average velocity at the

outlet as the output parameter. The optimal Space

Filling Design (OSFD) technique is selected because

of its ability to provide large amounts of information

The Optimized Geometry Solar Chimney as Passive Cooling Solution for Buildings in Jakarta

with a minimum number of numerical simulations

(Abdeen et al., 2019) [1].

Table 2. The minimum and maximum value of each input

parameters

Input Parameter

Minimum

Value

Maximum

Value

Inclination Angle (

) 25 75

Len

(

)

1,5 2,5

Width

(

)

0,5 3

Air Ga

(

)

0,1 0,3

2.4.2 Response Surface Method (RSM)

Response Surface Method (RSM) is a selected

approximation function that produces a correlation

between input and output parameters used by the

fitting algorithm indicated in DOEs methodology.

RSM is obtained using a second-order polynomial

regression model set and the results generated from

DOEs.

2.4.3 Optimization

After RSM is produced, optimization can be

performed using MOGA to derive the optimal design

based on the targets sets by maximizing the mass flow

rate and average air velocity on the outlet. MOGA is

an evolutionary algorithm with several objective

functions optimized simultaneously and subject to

inequality and equality constraints (ANSYS Fluent.

co, 2015) [3].

2.5 Simulation Results

The model based on the initial design generates

airflow 0,043 m

/s and average velocity on the output

0,405 m/s, as displayed in Figure 7. This simulation

shows air on the lower height of the chimney reaches

the maximum velocity value, and the velocity was

slower near absorber than near glass.

Figure 7. Velocity distribution on initial model design

2.5.1 Design of Experiments Results

DOEs method generates 25 design points and results

of the output parameters based on the setup from

Table 2. These design points showed in Table 3, and

the results were fed to RSM as data for the

interpolation approach to produces reasonably

accurate predictions.

Table 3. Design points generated from DOEs method

No.

Width

(m)

Inclination

Angle (

)

Air Gap

(m)

Length

(m)

1,05

44 0,104 1,88

2,55

58 0,112 1,92

0,85

54 0,224 1,56

1,45

72 0,272 1,96

1,25

60 0,12 2,32

2,65

56 0,152 2,4

1,75

66 0,24 2,44

2,95

42 0,184 1,72

0,65

36 0,176 2,16

2,05

46 0,296 2,24

2,25

30 0,128 2

0,55

64 0,2 2,08

1,15

70 0,136 1,76

2,45

32 0,264 1,8

2,15

74 0,168 2,12

0,95

38 0,28 1,84

1,65

40 0,16 2,48

1,85

48 0,144 1,52

1,35

28 0,192 1,68

1,95

52 0,288 1,64

2,75

34 0,216 2,28

2,35

68 0,208 1,6

2,85

62 0,248 2,04

0,75

50 0,256 2,36

1,55

26 0,232 2,2

2.5.2 Response Surface Method Results

From data generated in the DOEs method displayed

in Table 3. Each input and output parameter

correlation can be explored and

displayed in a

three-dimensional response chart, as showed in

Figure 8.

ICoSTE 2020 - the International Conference on Science, Technology, and Environment (ICoSTE)

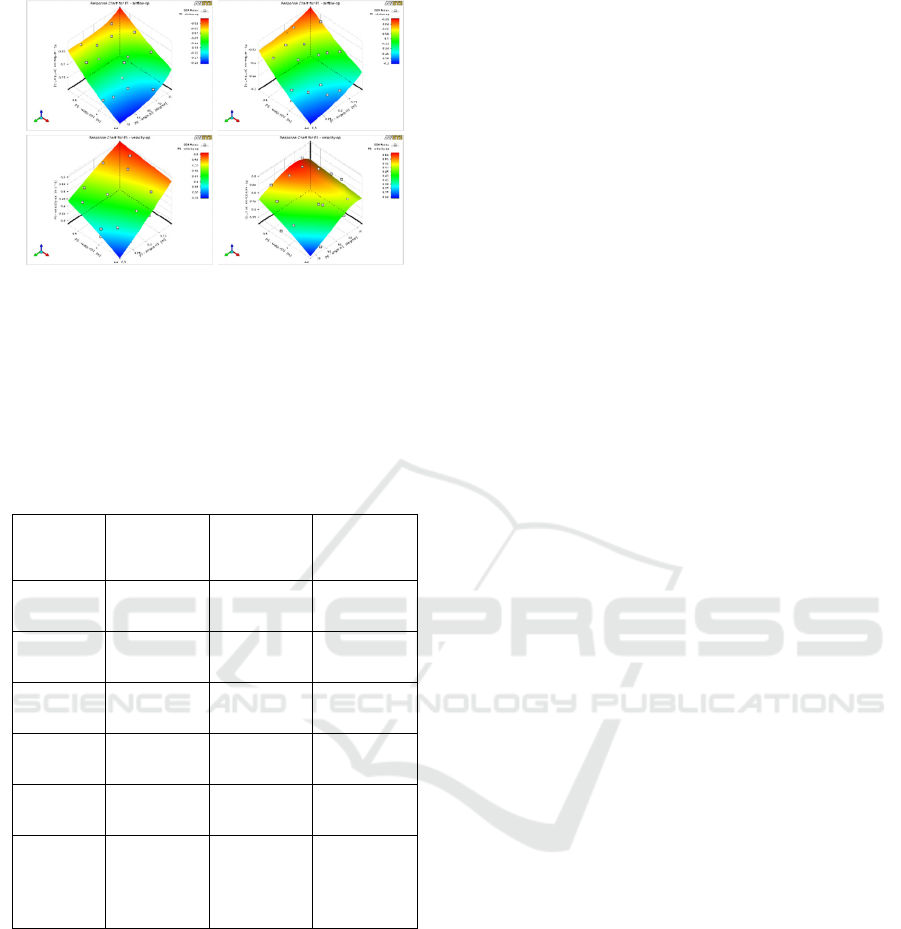
Figure 8. Response charts for airflow and velocity

2.5.3 Optimization Results

Three candidates from the optimization method used

MOGA by generating 10.000 designs to explore the

optimal solar chimney design by maximizing airflow

and average outlet velocity.

Table 4. Optimization candidates

Parameters Candidate 1 Candidate 2 Candidate 3

Width (m) 2,9986 2,986 2,9988

Inclination

Angle (

)

51,901 50,762 49,281

Air Gap

(m)

0,10228 0,10064 0,10151

Length

(m)

2,4966 2,4975 2,4934

Airflow

/s)

0,15952 0,15607 0,15488

Average

Velocity

on The

Outlet

(m/s)

0,61919 0,62593 0,62823

From the three candidates generated from MOGA,

there is a slight difference. Candidate 2 is chosen as

the best design because it maximizes airflow and

average outlet velocity.

3 CONCLUSIONS

In this research, a three-dimensional steady CFD

model was developed. Using the ANSYS® 2020 R2

FLUENT Design Exploration, an optimization

technique was used to increase the air velocity and

airflow from buoyancy effects inside the space. This

optimization method can integrate various chimney

parameters, including the height, width, inclination

angle, and air gap between the glass and the absorbing

wall. The optimal solar chimney is derived from the

optimization method, which features 51

inclination

angle, width 2,9988 m, air gap 0,1 m, chimney length

2,5 m. The ﬁnding highlights the potential and

advantages of employing this 3D optimization

technique to enhance natural ventilation solutions for

Jakarta buildings by passive solar chimneys.

REFERENCES

Abdeen, A, Serageldin, A, Ibrahim, M, El-Zafarany, A,

Ookawara, S, & Murata, R, (2019), Solar chimney

optimization for enhancing thermal comfort in Egypt:

An experimental and numerical study, Solar Energy,

524-536.

Chen, Q, (1995), Comparison of diﬀerent k-ε models for

indoor air ﬂow computations, Numerical Heat

Transfer, Part B: Fundamentals, 353-369.

ANSYS Fluent, co, (2015), ANSYS FLUENT Theory Guide

[WWW Document], Retrieved from

http://www,ansys,com/Products/Fluids/ANSYS-

Fluent.

The Optimized Geometry Solar Chimney as Passive Cooling Solution for Buildings in Jakarta