
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid
Aggregation Protocols
Fabian Knirsch
a
, Andreas Unterweger, Maximilian Unterrainer and Dominik Engel
Center for Secure Energy Informatics, Salzburg University of Applied Sciences, Urstein S
¨
ud 1, 5412 Puch/Hallein, Austria
Keywords:
Secure Aggregation, Paillier Cryptosystem, ElGamal Cryptosystem, Privacy.
Abstract:
Many smart grid applications require the collection of fine-grained load data from customers. In order to pro-
tect customer privacy, secure aggregation protocols have been proposed that aggregate data spatially without
allowing the aggregator to learn individual load data. Many of these protocols build on the Paillier cryptosys-
tem and its additively homomorphic property. Existing works provide little or no justification for the choice of
this cryptosystem and there is no direct performance comparison to other schemes that allow for an additively
homomorphic property. In this paper, we compare the ElGamal cryptosystem with the established Paillier
cryptosystem, both, conceptually and in terms of runtime, specifically for the use in privacy-preserving aggre-
gation protocols. We find that, in the ElGamal cryptosystem, when made additively homomorphic, the runtime
for encryption and decryption is distributed more asymmetrically between the smart meter and the aggregator
than it is in the Paillier cryptosystem. This better reflects the setup typically found in smart grid environments,
where encryption is performed on low-powered smart meters and decryption is usually performed on power-
ful machines. Thus, the ElGamal cryptosystem is a better, albeit overlooked, choice for secure aggregation
protocols.
1 INTRODUCTION
Collecting fine-grained load data from smart me-
ters installed in the customer premises has shown to
pose severe privacy risks (Wicker and Thomas, 2011;
McKenna et al., 2012; Burkhart et al., 2018). To mit-
igate them, secure aggregation protocols have been
proposed by many authors for privacy-preserving data
aggregation in the smart gird, e.g., (Li et al., 2010;
Erkin and Tsudik, 2012; Knirsch et al., 2017). These
protocols protect customer privacy by only providing
the sum of load data from a number of households at
one point in time (Buescher et al., 2017).
One approach for secure aggregation protocols is
to employ an additively homomorphic cryptosystem
and an entity that acts as a (semi-trusted) aggrega-
tor. Each smart meter encrypts its individual mea-
surement and sends the encrypted value to the aggre-
gator. The aggregator uses the additively homomor-
phic property of the underlying cryptosystem to cal-
culate the encrypted sum and forwards this sum to the
energy provider, who decrypts it. This way, the ag-
gregator does not learn individual meter readings, but
a
https://orcid.org/0000-0002-6346-5759
needs to be trusted for performing the correct aggre-
gation (Unterweger et al., 2019). Figure 1 shows the
principal setup and actors of such a smart grid aggre-
gation protocol.
Existing works, e.g., (Li et al., 2010; Erkin and
Tsudik, 2012; Erkin, 2015; Rane et al., 2015) provide
little or no justification for the choice of the cryptosys-
tem and most commonly employ the Paillier scheme
(Paillier, 1999). Only very few publications make
use of the ElGamal cryptosystem in the context of
smart grids, e.g., (Busom et al., 2016). To the best
of our knowledge, there exists no performance com-
parison between the Paillier cryptosystem and the El-
Gamal cryptosystem (ElGamal, 1985), which are the
two most commonly used homomorphic cryptosys-
tems (Armknecht et al., 2013) and also those with
the highest security guarantees (Fontaine and Galand,
2007).
While ElGamal is more lightweight in terms of
encryption complexity, it is multiplicative homo-
morphic, but can be made additively homomorphic
(Cramer et al., 1997). This can be advantageous for
low-powered devices such as smart meters. For this
reason, the ElGamal cryptosystem is already widely
employed in e-voting applications, as presented in
232
Knirsch, F., Unterweger, A., Unterrainer, M. and Engel, D.
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid Aggregation Protocols.
DOI: 10.5220/0008770902320239
In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 232-239
ISBN: 978-989-758-399-5; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

EP
A
SM
2
SM
1
. . .
SM
N
E (
∑
i
m
i
)
!
=
∏
i
E(m
i
)
E(m
1
)
E(m
2
)
E(m
N
)
Figure 1: Aggregation protocol with homomorphic encryp-
tion: Each smart meter (SM
i
) sends its encrypted value
E(m
i
) to the aggregator (A). The aggregator calculates the
sum of the values in the ciphertext domain using the addi-
tive homomorphic property of the cryptosystem. The result
is sent to the energy provider (EP) which decrypts it to ob-
tain the plaintext sum
∑
i
m
i
of the readings.
(Adida, 2008; Chaum et al., 2008; Culnane et al.,
2015).
1.1 Related Work
The properties of the Paillier cryptosystem have been
investigated in detail by, e.g., (Catalano et al., 2001;
Damg
˚
ard and Jurik, 2001; Damg
˚
ard et al., 2010).
The same is true for a number of variations of the
system, e.g., (Fouque et al., 2001; Galbraith, 2002;
Hazay et al., 2012). Similarly, investigations for the
ElGamal cryptosystem and its variations exist, e.g.,
(Cramer and Shoup, 2003; Kumar and Madrai, 2012;
Armknecht et al., 2013).
A general runtime comparison between the ElGa-
mal and the multiplicative homomorphic RSA cryp-
tosystem has been conducted by (Maqsood et al.,
2017). However, the Paillier cryptosystem has not
been considered in their analysis, as opposed to our
work.
A non-peer-reviewed publication titled “An exper-
imental study on Performance Evaluation of Asym-
metric Encryption Algorithms” by Farah et al. exists
which describes runtime results for both, the Paillier
and ElGamal cryptosystems. However, their reported
results do not increase with increasing plaintext size
and even drop to zero for some plaintexts, casting
doubts on their numbers and thus their conclusions.
To the best of our knowledge there is currently no
comparison of the Paillier and ElGamal cryptosystem
in the context of smart grid aggregation protocols and
no analysis of the suitability of the latter in practical
setups exists. Thus, this aspect is investigated in this
paper.
1.2 Contribution
This paper briefly presents both, the Paillier and the
ElGamal cryptosystems with extensions from the lit-
erature to make them comparable for additive homo-
morphic operations. The main contribution of this pa-
per is the runtime analysis and comparison of the two
cryptosystems for aggregated smart meter data. The
detailed analysis of encryption and decryption times
as well as of each relevant algorithmic step allows
for conclusions on the suitability and practicability of
both cryptosystems for secure aggregation. It also al-
lows for recommendations on which system to prefer
for this smart grid aggregation use case. In this paper,
we find that the ElGamal cryptosystem is overlooked
for many proposed protocols. The encryption is more
lightweight compared to Paillier cryptosystem and the
additional overhead at decryption can be mitigated by
powerful devices in the EP’s premises or is negligible
for practical applications.
1.3 Structure
The paper is structured as follows: Section 2 de-
scribes the Paillier and ElGamal cryptosystems, as
well as additional algorithms to make them compara-
ble. Section 3 compares both cryptosystems and their
application for privacy-preserving aggregation. Sec-
tion 4 summarizes the findings and gives an outlook
to future work.
2 BACKGROUND
In this section, the Paillier and ElGamal cryptosys-
tems, which are compared in this paper, are explained
briefly, together with their relevant properties. In ad-
dition, the Cramer transformation is described which
allows using the ElGamal cryptosystem in such a way
that it becomes comparable to the Paillier cryptosys-
tem. Furthermore, multiple algorithms for calculating
the aggregate after ElGamal decryption are described.
2.1 Paillier Cryptosystem
The Paillier cryptosystem is an additively homomor-
phic, semantically secure public-private key cryp-
tosystem (Paillier, 1999; Catalano et al., 2001).
An additively homomorphic cryptosystem fulfills the
equation
D(E(m
1
) ·E(m
2
)) = m
1
+ m
2
for two plaintexts m
1
and m
2
, where E and D denote
the encryption and decryption functions, respectively.
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid Aggregation Protocols
233

Given two large prime number p and q of the same
length, the public key (n, g) is calculated by
n = pq, g = n + 1
and the private key λ is calculated by
λ = ϕ(n), µ = ϕ(n)
−1
mod n,
where ϕ(n) = (p −1)(q −1).
Encryption of a plaintext m ∈{0, 1, . . . , n−1} to a
ciphertext c is performed by
c = g
m
r
n
mod n
2
,
with a random number r ∈ {1, 2, . . . , n −1}.
Given two ciphertexts c
1
and c
2
, the additive ho-
momorphic property can be shown by
c
1
·c
2
= g
m
1
+m
2
(r
1
·r
2
)
n
mod n
2
.
Decryption of the above expression will result in the
sum of m
1
and m
2
.
2.2 ElGamal Cryptosystem
The ElGamal cryptosystem is a public-private key
cryptosystem with a multiplicatively homomorphic
property (ElGamal, 1985). A multiplicatively homo-
morphic cryptosystem fulfills the equation
D(E(m
1
) ·E(m
2
)) = m
1
·m
2
.
Given a publicly known cyclic group G of order q
with a publicly known generator g, the public key is
h = g
r
,
with r ∈{1, 2, . . . , q −1} being randomly chosen. r is
the private key.
Encryption of a plaintext m to a ciphertext c is per-
formed by
c
1
= g
s
, c
2
= m ·h
s
,
with a randomly chosen s ∈ {1, 2, . . . , q −1}.
Calculating the product of two ciphertexts yields
the product of the corresponding plaintexts after de-
cryption.
2.3 Cramer Transformation
The ElGamal cryptosystem with its multiplicatively
homomorphic property can be transformed into an
additively homomorphic cryptosystem (like the Pail-
lier) scheme with the Cramer transformation (Cramer
et al., 1997).
The plaintext value to be encrypted must be in the
exponent. In practice, m can be transformed to m
0
by
m
0
= g
m
mod q.
The encryption is then applied to m
0
. Note, however,
that, after decryption, this yields g
∑
i
m
i
as a plaintext.
To solve the discrete logarithm and to retrieve the ac-
tual value
∑
i
m
i
, one of three recovery algorithms can
be applied: (i) Brute Force; (ii) Pollard’s Lambda; or
(iii) Baby Step Giant Step.
2.4 Brute Force Algorithm
To recover m from m
0
= g
m
(mod q) with known g
and q, the discrete logarithm log
g
(m
0
) = m (mod q)
can be solved by brute forcing all possible values of
m, until a solution is found. The complexity of this al-
gorithm is O(q). If it is known that m is within a given
interval [0, b], the complexity is reduced to O (b).
Linear speedup can be achieved by parallelizing
the brute-force search. While not reducing the com-
plexity itself, the constant factor of the runtime is re-
duced proportional to the number of parallel searches.
2.5 Pollard’s Lambda Algorithm
Pollard’s Lambda algorithm is designed to solve the
discrete logarithm and achieves a runtime complexity
of O
√
b −a
for a plaintext in the interval m ∈[a, b]
(Pollard, 1978). This assumes that m is with certainty
within the defined interval.
Pollard’s Lambda algorithm rewrites m = b + d −
d
k
(mod q) for a k ∈ [0, I −1]. I can be chosen ac-
cording to (Pollard, 1978). First, a sequence x
0...I
is
computed where x
0
= g
b
and
x
i+1
= x
i
g
f (x
i
)
,
with f being a parameterizable pseudorandom func-
tion. d is calculated as
d =
I−1
∑
i=0
f (x
i
).
Then, a sequence y
0...k
is computed where y
0
= m
0
,
y
i+1
= y
i
g
f (y
i
)
,
and additionally, a sequence d
0...k
is computed by
d
j
=
j−1
∑
i=0
f (y
i
).
If y
k
= x
I
(mod q), then m
0
g
d
k
= g
b+d
(mod q),
which equals g
m+d
k
= g
b+d
(mod q) and thus m =
b + d − d
k
(mod q). If k > I or d
i
> b − a + d
(mod q), the algorithm fails and the choice of f needs
to be adapted.
2.6 Baby Step Giant Step Algorithm
The Baby Step Giant Step algorithm is designed to
solve the discrete logarithm and achieves a runtime
complexity of O(
√
q), where q is the order of the
group (Shoup, 1997; Schnorr and Jakobsson, 2000).
m
0
= g
m
(mod q) (see previous section) can be
rewritten as m
0
= g
kx+l
(mod q) where x =
√
q
.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
234

The algorithm first computes g
l
(mod q) for 0 ≤l < x
and then tries the values 0 ≤ k < x until
g
l
= m
0
(g
−x
)
k
mod q
holds. This comparison is realized efficiently by hav-
ing a look-up table with the precomputed values of
g
l
.
3 COMPARISON
In this section, we compare the complexity and run-
time properties of the Paillier and ElGamal cryptosys-
tems in a setup typical for smart grid secure aggrega-
tion use cases.
For the comparison, we use a setup that reflects
typical capabilities that can be found in the field.
Smart meters are lightweight devices with limited
computational resources, whereas the EP can have
more powerful devices to decrypt and calculate the
aggregate, respectively. The setup for the comparison
is based on the aggregation protocol depicted in Fig-
ure 1, which reflects a setup commonly found in lit-
erature, see, e.g., (Li et al., 2010; Erkin, 2015; Rane
et al., 2015). Each smart meter encrypts its measure-
ment value using either the Paillier cryptosystem or
the ElGamal cryptosystem and submits the encrypted
values to an aggregator. The aggregator calculates the
product of these values and forwards the result to the
energy provider. The EP then decrypts the aggregate.
3.1 Evaluation Setup
Both cryptosystems, the Cramer transformation and
the recovery algorithm, are implemented in Java 8.
Measurements are performed on Windows 10 using
an Intel Core i7-6500U Processor
1
capable of running
4 threads. The following implementations are used
• Paillier Encryption Threshold Toolbox
2
. This
toolbox implements the Paillier cryptosystem and
also provides support for the thresholded variant.
• The ElGamal cryptosystem and the Cramer trans-
formation are implemented according to (Cramer
et al., 1997) and (ElGamal, 1985).
• Pollard’s Lambda algorithm is implemented ac-
cording to (Pollard, 1978).
1
https://ark.intel.com/products/88194/
Intel-Core-i7-6500U-Processor-4MCache-up-to-3
10-GHz
2
http://www.cs.utdallas.edu/dspl/cgi-bin/
pailliertoolbox/index.php
• The Baby Step Giant Step algorithm is a modified
version of an implementation from the University
of Maryland
3
, which can be extended in order to
support multiple threads.
The implementations for Paillier, ElGamal, Cramer
and the recovery algorithm only use the formulas as
in Section 2 without additional overhead. All of them
rely on the Java BigInteger class
4
and its perfor-
mance, so that the time required for the calculations
is comparable.
The current recommended key length for cryp-
tosystems based on the discrete logarithm problem to
be secure for the year 2030 and beyond is 3072 bits
according to (Barker, 2016). As this applies to both,
the Paillier cryptosystem (Paillier, 1999) and the El-
Gamal cryptosystem (ElGamal, 1985), a key length
of 3072 bits is used for the evaluation.
All measurements are repeated 110 times in order
to minimize external factors on the mean value. The
first ten measurement values are discarded to mitigate
cache-warming effects of the Java Virtual Machine.
3.2 Paillier and ElGamal Runtime
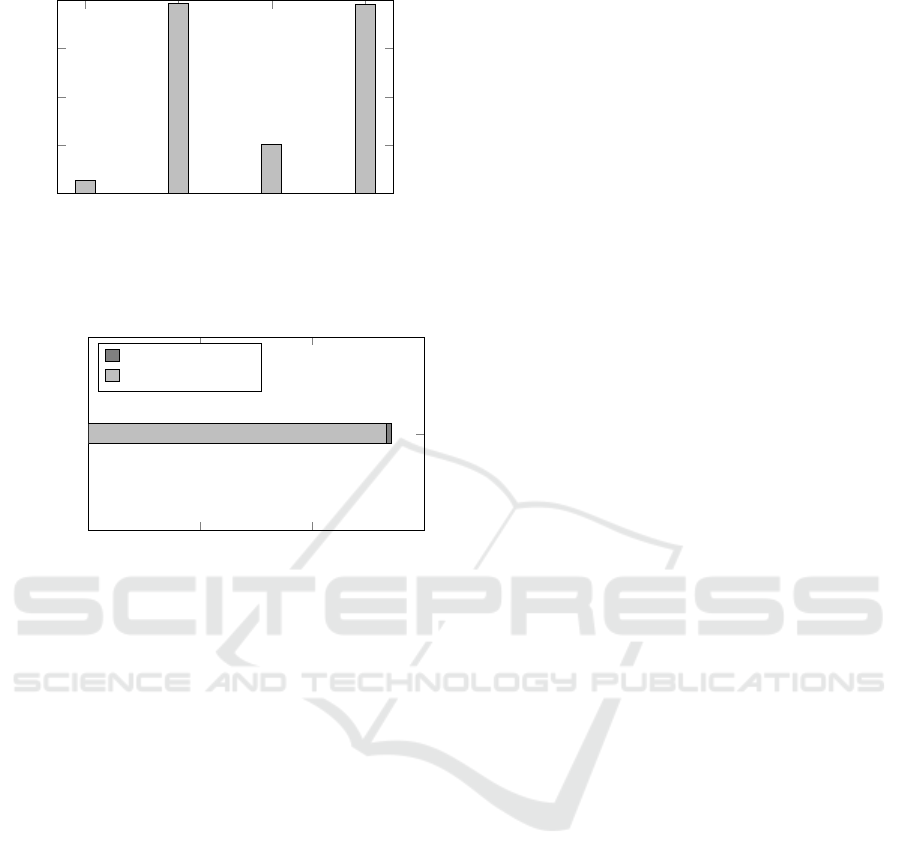
Figure 2 depicts the runtimes for encryption and de-
cryption of the Paillier and ElGamal cryptosystems. It
is clear that the encryption time for the ElGamal cryp-
tosystem is more than one order of magnitude smaller
(approximately one 15
th
) than that of the Paillier cryp-
tosystem. The reason for this discrepancy is the much
smaller range in the size of the exponent for which
the calculations for the ElGamal encryption are per-
formed (see Section 2).
However, in order to allow for an additively ho-
momorphic property for the ElGamal cryptosystem,
the Cramer transformation as described in Section 2
needs to be applied to the plaintext value. This is
already included in the values depicted in Figure 2.
Figure 3 shows how large the runtime portion for
this transformation (0.042 ms) is compared to the to-
tal runtime (2.709 ms). This portion is negligible in
practice.
Similar to the encryption runtime, the decryption
time for the ElGamal cryptosystem is lower than that
of the Paillier cryptosystem. The runtime is about one
fourth. Note that the result of the decryption is, how-
ever, not the sum of the plaintext values
∑
i
m
i
, but
rather g
∑
i
m
i
. Thus, one of the recovery algorithms
mentioned in Section 2 (e.g., Brute Force algorithm)
needs to be applied, which incurs additional runtime.
3
https://www.csee.umbc.edu/
∼
stephens/crypto/
CIPHERS/BigIntegerMath.java
4
https://docs.oracle.com/javase/8/docs/api/java/math/
BigInteger.html
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid Aggregation Protocols
235
ElGamal Paillier ElGamal Paillier
0
10
20
30
40
Encryption Decryption
Runtime in ms
Figure 2: Comparison of encryption and decryption run-
times for the ElGamal cryptosystem and the Paillier cryp-
tosystem.
0 1 2 3
ElGamal
Runtime in ms
Cramer transformation
ElGamal encryption
Figure 3: Breakdown of runtime for the steps of ElGamal
encryption.
3.3 Recovery Runtime
After decryption, the EP has to apply a recovery al-
gorithm for retrieving the actual sum of the values.
In order to assess the required runtime for this step,
an aggregation group size (number of smart meters
N) and a value range (size of m
i
) that is representa-
tive for real-world applications (Erkin, 2015) (and is
commonly used in related work (Knirsch et al., 2018;
Buescher et al., 2017)) are used: Each measurement
m
i
is 16 bits in size and the aggregation group size N
(number of smart meters) is varied between one and
2
7
= 128. Aggregating 16-bit values with these group
sizes results in measurement sums
∑
i
m
i
between 2
16
and 2
23
.
Note that the EP can have powerful devices to
perform the calculations and thus any recovery algo-
rithm can be implemented efficiently using multiple
threads. For our analysis, the value range is split into
T ∈ {1, 2, 4} intervals of equal length and one thread
is used per interval. The number of threads is limited
by the properties of the processor.
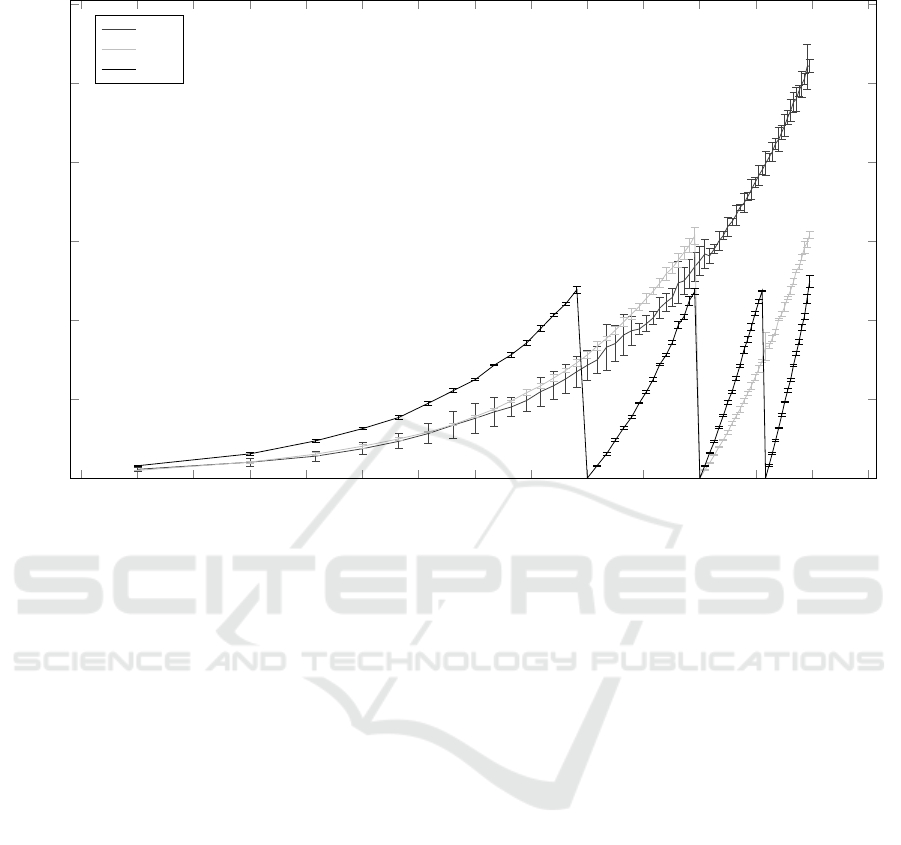
Figure 4 shows runtimes for the Brute Force algo-
rithm with a varying number of threads. The vertical
bars denote the standard deviation for each point.
Each thread starts at a defined value, e.g., m = 2
16
for the first thread, calculates the discrete logarithm
and then increases this value by one in each step until
m
0
is found. For T = 1, the entire space of the mea-
surement sum is thus searched linearly. The runtime
increases nearly linearly with the size of
∑
i
m
i
(note
that both axes are logarithmic).
Increasing the number of threads incurs a near
constant overhead for starting the additional threads.
This leads to higher runtimes for small values of
∑
i
m
i
. However, this allows partitioning the search
space and thus running the recovery algorithm in par-
allel.
Running the algorithm in parallel leads to earlier
recoveries. Once
∑
i
m
i
has been successfully recov-
ered, all threads can be stopped. It can be seen that a
higher number of threads in general improves runtime
for larger values of
∑
i
m
i
. For example, the worst case
runtime for one thread is 104.5 s, while it is 49.9 s for
four threads. It can also be seen from the results that
the choice of the starting value for a thread signifi-
cantly impacts the time needed for recovery. Since
for practical applications an interval for
∑
i
m
i
can be
guessed, this will improve overall performance.
While the Brute Force algorithm only provides a
baseline which can be outperformed by more efficient
algorithms, such as Baby Step Giant Step and Pol-
lard’s Lambda, it can be seen that the time needed for
recovering the sum of the measurements is below 50 s
even for the largest value of
∑
i
m
i
using four threads.
Other algorithms for recovery as described in Sec-
tion 2 can be used. This will further reduce the
complexity, but not necessarily the runtime for this
step. For the Baby Step Giant Step algorithm and
Pollard’s Lambda algorithm in the practical evalua-
tion we could not find suitable algorithm parameters
for which any value bit size could be processed faster
than Brute Force.
Alternatively, due to the comparably small range
of
∑
i
m
i
(i.e., a small plaintext space), a lookup ta-
ble can be constructed that stores all possible values
for g
∑
i
m
i
and the corresponding exponent. This al-
lows trading additional memory consumption against
access time (Croman et al., 2016). In particular,
an access complexity of O(1) can be achieved with
3095 MiB of additional memory with 2
23
entries map-
ping one 3072 bit ciphertext to one 23 bit plaintext
each.
However, as the results for the Brute Force al-
gorithm are already practically feasible, the use of a
lookup table is not necessary and the fine-tuning of
the parameters of the Baby Step Giant Step algorithm
and Pollard’s Lambda algorithm remain future work.
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
236
16.5
17
17.5
18
18.5
19
19.5
20
20.5
21
21.5
22
22.5
23
23.5
0
0.2
0.4
0.6
0.8
1
1.2
·10
5
Size of
∑
i
m
i
in bits
Runtime in ms
T = 1
T = 2
T = 4
Figure 4: Runtime for the Brute Force algorithm after ElGamal decryption with a variable number of threads T . The vertical
bars denote the standard deviation.
3.4 Combined Runtime
The combined runtime is the time needed for decryp-
tion in case of the Paillier cryptosystem and the El-
Gamal cryptosystem as well as the additional time
needed for recovery when using the latter.
Table 1 summarizes the runtimes for SM and EP
for both cryptosystems. It can be seen that the Paillier
cryptosystem requires about 15 times the runtime for
encryption compared to the ElGamal cryptosystem,
but performs equally for encryption and decryption.
On low-powered smart meters, this gives the ElGamal
cryptosystem a significant advantage over the Paillier
cryptosystem.
In Section 3.2 the ElGamal decryption runtime is
found to be 10.179 ms. The time needed for recov-
ery is at most 49930 ms (from Section 3.3). Thus, the
combined runtime is always below 50 s. In most Eu-
ropean countries, measurements of one day are sub-
mitted only once per day (see e.g., (Nationalrat, 2010;
Bundestag, 2016)). Hence, the aggregator has a time
frame of 24 hours to recover the sum before the val-
ues of the next day need to be processed. Even for
real-time network stability monitoring with 15 minute
intervals, the combined runtime is comparably small.
Note that the measurements above have been per-
formed on consumer-grade hardware and in a practi-
cal setup much more powerful hardware is used, fur-
ther reducing the runtime.
4 CONCLUSION
Both, the Paillier and the ElGamal cryptosystem are
suitable for secure aggregation protocols in the smart
grid due to the ability to enable additively homomor-
phic operations. For encryption, the ElGamal cryp-
tosystem is significantly (more than one order of mag-
nitude) faster than the Paillier cryptosystem. This
is highly beneficial for low-powered devices such as
smart meters. For decryption, the Paillier cryptosys-
tem is significantly faster overall. However, decryp-
tion is performed by energy providers, which typi-
cally host large-scale servers for this purpose where
runtime is not as crucial as it is on smart meters.
Even on significantly less powerful consumer-grade
hardware, the additonal runtime required for recov-
ery when using the ElGamal cryptosystem is small
enough in practical setups. In summary, the ElGa-
mal cryptosystem is to be preferred for such smart
grid use cases, despite the Paillier cryptosystem be-
ing commonly used.
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid Aggregation Protocols
237

Table 1: Worst-case runtimes in seconds (rounded) with four significant digits for all operations involving encryption and
decryption for the ElGamal and Paillier cryptosystems.
ElGamal Paillier
SM runtime [s] EP runtime [s] SM runtime [s] EP runtime [s]
Encryption 0.003 – 0.039 –
Decryption – 0.010 – 0.039
Cramer transformation 0.000 – – –
Recovery algorithm – 49.930 – –
Total 0.003 49.940 0.039 0.039
ACKNOWLEDGEMENTS
The financial support by the Federal State of Salzburg
is gratefully acknowledged.
REFERENCES
Adida, B. (2008). Helios : Web-based Open-Audit Voting.
In USENIX Security Symposium, volume 17, pages
335–348.
Armknecht, F., Katzenbeisser, S., and Peter, A. (2013).
Group homomorphic encryption: Characterizations,
impossibility results, and applications. Designs,
Codes, and Cryptography, 67:209–232.
Barker, A. (2016). NIST Special Publication 800-57: Rec-
ommendation for Key Management - Part 1: General
(Revised).
Buescher, N., Boukoros, S., Bauregger, S., and Katzen-
beisser, S. (2017). Two Is Not Enough: Privacy As-
sessment of Aggregation Schemes in Smart Meter-
ing. Proceedings on Privacy Enhancing Technologies,
2017(4):118–134.
Bundestag (2016). Gesetz zur Digitalisierung der En-
ergiewende. Bundesgesetzblatt Teil I, 2016(43):2034–
2064.
Burkhart, S., Unterweger, A., Eibl, G., and Engel, D.
(2018). Detecting Swimming Pools in 15-Minute
Load Data. In 17th IEEE International Conference
On Trust, Security And Privacy In Computing And
Communications (TrustCom 2018), pages 1651–1655,
New York, NY, USA. IEEE.
Busom, N., Petrlic, R., Seb
´
e, F., Sorge, C., and Valls, M.
(2016). Efficient smart metering based on homomor-
phic encryption. Computer Communications, 82:95–
101.
Catalano, D., Howgrave-graham, R. G. N., and Nguyen,
P. Q. (2001). Paillier’s Cryptosystem Revisited. In
Proceedings of the 8th ACM conference on Computer
and Communications Security, pages 206–214. ACM.
Chaum, D., Carback, R., Clark, J., Essex, A., Popoveniuc,
S., Rivest, R. L., Ryan, P. Y. A., Shen, E., and Sher-
man, A. T. (2008). Scantegrity II: End-to-End Veri-
fiability for Optical Scan Election Systems using In-
visible Ink Confirmation Codes. In USENIX Security
Symposium, volume 8, pages 1–13.
Cramer, R., Gennaro, R., and Schoenmakers, B. (1997). A
Secure and Optimally Efficient Multi-Authority Elec-
tion Scheme. In Proceedings of the 16th Annual In-
ternational Conference on Theory and Application of
Cryptographic Techniques, EUROCRYPT’97, pages
103–118, Konstanz, Germany. Springer-Verlag.
Cramer, R. and Shoup, V. (2003). Design and Analysis
of Practical Public-Key Encryption Schemes Secure
against Adaptive Chosen Ciphertext Attack. SIAM
Journal on Computing, 33:167–226.
Croman, K., Decker, C., Eyal, I., Gencer, A. E., Juels, A.,
Kosba, A., Miller, A., Saxena, P., Shi, E., G
¨
un Sirer,
E., Song, D., and Wattenhofer, R. (2016). On Scaling
Decentralized Blockchains. In International Confer-
ence on Financial Cryptography and Data Security,
pages 106–125, Christ Church, Barbados. Springer.
Culnane, C., Ryan, P. Y. A., Schneider, S., and Teague, V.
(2015). vVote: a Verifiable Voting System. ACM
Transactions on Information and System Security
(TISSEC), 18(1).
Damg
˚
ard, I., Jurik, M., and Buus, J. (2010). A generaliza-
tion of Paillier ’ s public-key system with applications
to electronic voting. International Journal of Infor-
mation Security, pages 371–385.
Damg
˚
ard, I. and Jurik, M. J. (2001). A Generalisation,
a Simplification and some Applications of Paillier’s
Probabilistic Public-Key System. In PKC 2001: Pub-
lic Key Cryptography, pages 119–136.
ElGamal, T. (1985). A Public Key Cryptosystem and a Sig-
nature Scheme Based on Discrete Logarithms. IEEE
Transactions on Information Theory, 31(4):469–472.
Erkin, Z. (2015). Private Data Aggregation with Groups for
Smart Grids in a Dynamic Setting using CRT. In 2015
IEEE International Workshop on Information Foren-
sics and Security (WIFS), Rome, Italy. IEEE.
Erkin, Z. and Tsudik, G. (2012). Private Computation of
Spatial and Temporal Power Consumption with Smart
Meters. In Bao, F., Samarati, P., and Zhou, J., ed-
itors, Proceedings of the 10th international confer-
ence on Applied Cryptography and Network Security,
ACNS’12, pages 561–577. Springer, Berlin Heidel-
berg.
Fontaine, C. and Galand, F. (2007). A Survey of Homomor-
phic Encryption for Nonspecialists. EURASIP Journal
on Information Security.
Fouque, P. a., Poupard, G., and Stern, J. (2001). Sharing de-
ICISSP 2020 - 6th International Conference on Information Systems Security and Privacy
238

cryption in the context of voting or lotteries. Financial
Cryptography, pages 90–104.
Galbraith, S. D. (2002). Elliptic curve Paillier schemes.
Journal of Cryptology, pages 1–10.
Hazay, C., Mikkelsen, G. L., Rabin, T., and Toft, T. (2012).
Efficient RSA key generation and threshold Paillier
in the two-party setting. Lecture Notes in Computer
Science (including subseries Lecture Notes in Artifi-
cial Intelligence and Lecture Notes in Bioinformatics),
7178 LNCS:313–331.
Knirsch, F., Eibl, G., and Engel, D. (2018). Error-
resilient Masking Approaches for Privacy Preserving
Data Aggregation. IEEE Transactions on Smart Grid,
9(4):3351–3361.
Knirsch, F., Engel, D., and Erkin, Z. (2017). A Fault-
tolerant and Efficient Scheme for Data Aggregation
Over Groups in the Smart Grid. In 9th IEEE Interna-
tional Workshop on Information Forensics and Secu-
rity (WIFS), pages 1–6, Rennes, France. IEEE.
Kumar, V. and Madrai, S. (2012). Secure Hierarchical Data
Aggregation in Wireless Sensor Networks : Perfor-
mance Evaluation and Analysis. 13th International
Conference on Mobile Data Management, pages 196–
201.
Li, F., Luo, B., and Liu, P. (2010). Secure Information Ag-
gregation for Smart Grids Using Homomorphic En-
cryption. In Proceedings of First IEEE International
Conference on Smart Grid Communications, pages
327–332, Gaithersburg, Maryland, USA. IEEE.
Maqsood, F., Ahmed, M., Ali, M. M., and Shah, M. A.
(2017). Cryptography: A Comparative Analy-
sis for Modern Techniques. International Journal
of Advanced Computer Science and Applications,
8(6):442–448.
McKenna, E., Richardson, I., and Thomson, M. (2012).
Smart meter data: Balancing consumer privacy con-
cerns with legitimate applications. Energy Policy,
41:807–814.
Nationalrat (2010). Bundesgesetz, mit dem die Organ-
isation auf dem Gebiet der Elektrizit
¨
atswirtschaft
neu geregelt wird (Elektrizit
¨
atswirtschafts- und -
organisationsgesetz 2010 – ElWOG 2010). BGBl. I
Nr. 110/2010 (NR: GP XXIV RV 994 AB 997 S. 86.
BR: 8420 AB 8421 S. 791.).
Paillier, P. (1999). Public-Key Cryptosystems Based on
Composite Degree Residuosity Classes. In Stern, J.,
editor, Advances in Cryptology — EUROCRYPT ’99,
volume 1592 of Lecture Notes in Computer Science,
pages 223–238. Springer, Berlin Heidelberg.
Pollard, B. J. M. (1978). Monte Carlo Methods for Index
Computation (mod p). 32(143):918–924.
Rane, S., Freudiger, J., Brito, A. E., and Uzun, E. (2015).
Privacy , Efficiency & Fault Tolerance in Aggregate
Computations on Massive Star Networks. In 7th IEEE
International Workshop on Information Forensics and
Security (WIFS), pages 1–6, Rome, Italy. IEEE.
Schnorr, C. P. and Jakobsson, M. (2000). Security of Signed
ElGamal Encryption. In Okamoto, T., editor, Ad-
vances in Cryptology - ASIACRYPT 2000, pages 73–
89, Berlin Heidelberg. Springer Berlin Heidelberg.
Shoup, V. (1997). Lower Bounds for Discrete Logarithms
and Related Problems. In Fumy, W., editor, Advances
in Cryptology - EUROCRYPT ’97, pages 256–266,
Berlin Heidelberg. Springer Berlin Heidelberg.
Unterweger, A., Taheri-Boshrooyeh, S., Eibl, G., Knirsch,
F., K
¨
upc¸
¨
u, A., and Engel, D. (2019). Understanding
Game-Based Privacy Proofs for Energy Consumption
Aggregation Protocols. IEEE Transactions on Smart
Grid, 10(5):5514–5523.
Wicker, S. B. and Thomas, R. (2011). A privacy-aware ar-
chitecture for demand response systems. In Proceed-
ings of the Annual Hawaii International Conference
on System Sciences, Koloa, HI, USA. IEEE.
Comparison of the Paillier and ElGamal Cryptosystems for Smart Grid Aggregation Protocols
239
