
Implementation of a Memetic Algorithm to Optimize the Loading of
Kilns for the Sanitary Ware Production
Natalia Palomares
1a
, Rony Cueva
1b
, Manuel Tupia
1c
and Mariuxi Bruzza
2d
1
Department of Engineering, Pontificia Universidad Católica del Perú, Av. Universitaria 1801, Lima, Peru
2
Faculty of Hospitality and Tourism, Universidad Laica “Eloy Alfaro” de Manabí, C. Universitaria S/N, Manabí, Ecuador
Keywords: Memetic Algorithm, Combinatorial Optimization, Artificial Intelligence, Scheduling, Production Planning.
Abstract: One of the most important aspects to be considered in the production lines of sanitaries is the optimization in
the use of critical resources such as kilns (industrial furnaces) due to the complexity of their management
(they are turned on twice a year) and the costs incurred. The manufacturing processes of products within these
kilns require that the capacity be maximized by trying to reduce downtime. In this sense, Artificial Intelligence
provides bioinspired and evolutionary optimization algorithms which can handle these complex variable
scenarios, the memetic algorithms being one of the main means for task scheduling. In present investigation,
and based on previous works of the authors, a memetic algorithm is presented for optimization in the loading
of kilns starting from a real production line.
1 INTRODUCTION
The never-ending competition among the companies
from the ceramic and sanitary ware manufacturing
industry has prompted these companies to seek to
improve their quality and efficiency in the production
process, so as to increase their revenues and minimize
losses (Porras, 2018). The use of computer solutions
is a fine example of this quest. However, although
these focus on several aspects such as staff
management, storage, sales records and so on, there
is still a gap in the optimization of the manufacturing
process stages.
This is the case of the firing stage that takes the
longest and lacks a strategy for an optimum selection
of pieces to be loaded into the kiln. As a result a
bottleneck occurs in the process. The variety of
models to be manufactured, number of pieces, colors
as well as demand, weight and volume constraints (of
kiln cars and kilns) makes pieces selection a
challenge (Leon, Cueva, Tupia & Paiva Dias, 2019).
This problem does not only emerge in the sanitary
ware manufacturing industry but also in others fields
where products composed of several parts are
a
https://orcid.org/0000-0001-5279-4613
b
https://orcid.org/0000-0003-4861-571X
c
https://orcid.org/0000-0001-5260-2829
d
https://orcid.org/0000-0002-1470-8515
manufactured and assembled. That is why several
researches have been conducted to develop
algorithm-based solutions that generate good results
within reasonable times.
The most commonly used type of algorithms in
these cases are metaheuristic ones. Within this
category the genetic algorithm is the preferred one
because of its simplicity. However, recent researches
have shown that memetic algorithms produce positive
solutions in a lower number of evaluations but with
better quality.
This paper has taken into account the
aforementioned and puts forward the design and the
implementation of a memetic algorithm that
generates a selection of pieces prioritizing those that
take advantage of the capacity of the kilns and kiln
cars weight and volume, considering the demand of
product sets. This algorithm was then calibrated to
improve it and, finally, was compared to a genetic
algorithm to determinate which was the best suited to
tackle this type of problem.
The memetic algorithm (MA) was chosen because
of its advantages like exploitation of problem-
knowledge (Moscato & Cotta, 2003) and improved
Palomares, N., Cueva, R., Tupia, M. and Bruzza, M.
Implementation of a Memetic Algorithm to Optimize the Loading of Kilns for the Sanitary Ware Production.
DOI: 10.5220/0008875203050312
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 305-312
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
305

procedures for local search, which lead to a faster
convergence and a statistically better solution (Wrona
& Pawełczyk, 2013). In addition, it’s easy to
implement and more efficent and efective than
traditional evolutionary algorithms (Zhang, Sun, &
Wang, 2009). And the genetic algorithm its used to
compared it to the MA because it’s one of the most
used algorithms to solve combinatorial optimization
problems due to its robust nature and how easy it is to
implement (Zhang, Sun, & Wang, 2009).
This paper is organized in the following manner:
Section 2 addresses the issues and their impact on the
industry; Section 3 displays the problem state-of-the-
art; Section 4 introduces the proposed algorithm and
finally Section 5 deals with the numeric
experimentation this algorithm went through. In the
end, the project conclusions will be introduced.
2 PROBLEM DESCRIPTION
2.1 Current Situation
The sanitary ware manufacturing sector is
characterized by a wide variety of products offered in
different models, colors and sizes (Regalado, Maroto,
Ruiz, & García del Río, 2011). Items may be
composed of one or more pieces. Products of the
same model and color pooled into sets are sold.
That is why – and because of the increase of data
volume required to manage the value change – the
sanitary ware manufacturing industry has
increasingly used computer solutions aligned to the
industry´s characteristics (Ceramic Industry, 2015).
Nevertheless, many of them are not focused on the
optimization of the production process itself.
This process has several stages, including firing,
which lasts the longest (Diaz, 2004). Within this
stage, the selection of pieces is the most important
step, which is quite complex since there are several
factors to be considered such as demand, variety of
models to be manufactured, number of pieces
comprised, colors, products sets as well as weight and
volume constraints in kiln cars and kilns.
Kilns used in sanitary ware manufacturing are
rectilinear channels oriented to continuous
production (Gómez Gutiérrez, C., 2010) where kiln
cars are introduced. These cars have plates or shelves
where pieces are put so that they don’t stick together
(Rhodes, 2004). In this paper, these specific places
where pieces are put are called compartments.
The lack of a strategy for an optimum selection of
pieces causes a bottleneck. And this bottleneck is the
problem to be solved (Monzon, Cueva, Tupia &
Bruzza, 2019).
2.2 Impact on the Sanitary Ware
Manufacturing Industry
The lack of a selection strategy results in choosing
pieces of only one model or color as well as the
production delay of other models.
Under other circumstances, pieces of different
models and colors are chosen but do not form any set,
thus delaying subsequent stages of assembly and
packaging. This also causes delayed production,
affecting selling and as a result only a few complete
models are in storage but with a huge amount of
incomplete sets and loose pieces as well. As a
consequence, clients are not timely serviced and
supply takes too long, sells are lost, and in addition
fines for delays, higher storage cost and
underutilization of the production capacity occur
(Savsar & Abdulmalek, 2008).
3 BRIEF SUMMARY OF
STATE-OF-THE-ART
The current issue regarding the selection of pieces
stage is of a combinatorial optimization type, known
as the knapsack problem, which is highly complex
and is considered as NP-difficult (Fuentes, Vélez,
Moreno, Martínez & Sánchez, 2015). The knapsack
problem consists of selecting a set of items that meet
the constraints and generate the greatest benefit
(Dorta, León, Rodríguez & Rojas, 2003).
Other industries, such as foundries and factories
that produce a vast array of products composed of
several parts to be later assembled, also pose similar
difficulties (Tupia, Cueva & Guanira, 2017). This is
the cause for researches have been conducted that
although they do not exactly cover the same problem,
they intend to solve similar problems (Koblasa,
Vavrousek, & Manlig, 2017) (Baiqing, Haixing,
Shaobu, Yifei, & Fei, 2016). The solutions proposal
they put forward is the use of metaheuristics that have
the advantage to be not specific to a problem but
provide good solutions within a reasonable time
(Blum & Roli, 2003).
Among the proposed metaheuristics, the most
commonly used method with the best results is the
genetic algorithm (Liu, Pan & Chai, 2015) (Duda &
Stawowy, 2013). This algorithm was developed by
Holland and is inspired in Charles Darwin’s theory of
evolution (Holland, 1992); among its advantages are
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
306

simplicity, global perspective and intrinsic processing
(Deb, 2004).
This method has been used to solve similar
problems. For example, Liu, Pan & Chai put forward
a specialized genetic algorithm (SGA) for the
grouping of work orders, taking into account factors
such as deadline, priority and demand (Liu, Pan &
Chai, 2015). Wang, Ma, Luo & Qin introduced a new
HGA-OVNS metaheuristics, which is the
hybridization of the genetic algorithm, the Variable
Neighborhood Search (VNS) and the Optimization
Based Learning (OBL) to deal with the production
planning problem in an assembly plant (Wang, Ma,
Luo & Qin, 2016). Duda & Stawowy developed a
genetic algorithm to optimize the selection of alloys
and products to be manufactured in a foundry (Duda
& Stawowy, 2013). In all the researches mentioned,
the genetic algorithm was compared to other
algorithms and even with commercial software. The
outcome was that the genetic algorithm showed a
better performance and generated better quality
solutions.
Another algorithm successfully used in similar
issues is the memetic one, which combines Local
Search with genetic operators (Alba & Dorronsoro,
2005), balancing the exploration skills of
evolutionary algorithms with the exploitation skills of
the local search (Krasnogor & Smith). That is why, a
lower number of evaluations is required to find top
quality optima and solutions (Baesler & Palma,
2014).
4 PROPOSED ALGORITHMS
4.1 Data Structure
A structure is required that specifies which pieces will
be loaded into the kiln. Each of the pieces will be
placed in a different compartment, and there may be
several pieces of the same type in the selected group.
Therefore, the solution’s structure has been
defined as a 2-dimensional matrix (compartment x
kiln car). See Figure 1.
Figure 1: Solution data structure.
Each row is identified with a specific
compartment: the first row contains all the pieces that
will be placed in compartment 1; the second row, the
compartment 2 and so on. In the case of the columns,
each column represents a kiln car: column 1
represents the kiln car 1; column 2, kiln car 2 and so
on.
The value within each of the cells is the code of
the piece that will go in a specific compartment and
in a specific kiln car. For example: in Figure 1, value
y represents a piece with code y that has been placed
in the compartment 3 in the first kiln car. The value 0
has been placed in empty compartments.
4.2 Proposed Memetic Algorithm
The pseudocode of the memetic algorithm is the
following:
Figure 2: Memetic Algorithm.
This algorithm takes as the initial parameter the
population generated by a GRASP algorithm and it
extracts the best solution (currentBest) from this
population.
Then, it generates a new population (newPop)
through the application of crossover operators,
mutation and local search in the current population
(pop).
Afterwards, it unifies the previous population
with the new one to obtain another population with
the best solution from both, and seeks the best
solution of this population for any improvement with
respect to the previous generation; if no improvement
is seen, the gNoImprovement counter will be
increased.
Implementation of a Memetic Algorithm to Optimize the Loading of Kilns for the Sanitary Ware Production
307

Finally, the algorithm checks if the no
improvement generation limit is reached. If so, the
conclusion is that the population degenerated (i.e., it
comes to a standstill in a local optimun) so that it will
be restored.
This process will be repeated until complying with
any of the stop conditions: reaching the maximun
number of generations or exceeding the deadline.
4.3 Brief Discussion of the Algorithm
The operators used in the memetic algortihm are
below:
Selection operator: it chooses individuals to be
affected by the recombination operator and chooses
the solutions the local search will be applied to. For
the selection the roulette method is used, allocating
each solution a circular sector of the roulette
proportional to its fitness value in such a manner that
when spinning it the best solutions will have a higher
likelihood. The roulette implemented has a binary
search and in the worst case scenario it will require
O(log n) comparisons to find the selected value
(Lipowski & Lipowska, 2012).
Recombination operator: used to make up a new
population. It uses individuals chosen by the selection
operator and takes the crossover rate as its parameter,
which determines the number of times to be applied.
To carry out the operation the uniform recombination
will be applied, thus generating a random number
between 0 and 1 for each element that is part of the
solution. If this number is lower than p
c
, the element of
the first father is then allocated to the first son and that
of the second father to the second son, otherwise the
allocation will be reversed (Magalhaes-Mendes, 2013).
Mutation operator: it slightly modifies a solution;
using a mutation rate and a randomly generated value
from 0 to 1; if the generated value is lower than the
rate (mutationRate), the operator will be applied. The
mutation will replace an item assigned by another one
that fits in the same compartment.
Local search operator: it uses the k-opt heuristics
that replaces k elements present in the current
solution with others that are not part thereof. Based
on the Ishibuchi, Tanigaki, et al. research, this search
will be conducted each gLs iteration, and will be
applied to a reduced number of individuals from the
population (determined by probLs variable) and will
only visit nLs neighbors (Ishibuchi, et. al, 2013).
4.3.1 Generation of a New Population
Figure 3 shows the pseudocode of the function that
generates a new population.
Figure 3: Generate new population.
4.3.2 Updating of Population
Once the new population (newPop) is generated, this
will be unified by the current (pop) one, selecting the
best elements of both populations to form a group
composed of the same number of individuals as the
current population.
The addition strategy is chosen because it is fast,
does not require a population of a high number of
offspring and ensures that values of the target
function do not get worse (Datoussaid, Verlinden &
Conti, 2002).
4.3.3 Restoration of Population
A small percentage is preserved with the best
solutions of the current population and the remainder
is disposed. To complete the population, new
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
308
solutions are generated through the GRASP
algorithm, these will be mutated before they are
added up to the population.
4.4 Mathematical Model
The target function chooses the selection of pieces
that maximize demand satisfaction, kiln volume and
kiln car weigh capacity use. The target function is:
∗
∑
∑
(1)
where:
(2)
,
∀
1,∀∈,∀∈
(3)
∑
∑
(4)
,
(5)
:1.. (6)
1,0
,0
,
10100
(7)
Equation 2, defines sum of selected pieces
considering penalties (m). Equation 3, establishes the
average priority of piece y is equal to the average
priority of the set it belongs to, which is the average
priority of requests and considers the amount
requested, the proximity of delivery and the customer
priority level (as defined in Equation 4). Equation 5,
constraints the number of pieces y considered in the
sum in SP to the necessary amount to satisfy the
demand. Equation 7 defines a function that returns an
integer value between 0 to 10 according to demand
pending to be satisfied.
Table 1: Variables definition.
CV, CW,
CD
Coefficients that add up 1 and represent
the importance of volume factor, weight
and demand.
MaxKilnVol Maximum kiln volume.
MaxCarW Maximum weight supported by kiln car.
MaxCPrior Maximum value of the addition of
priorities of pieces that can be loaded
into a kiln car.
W
i
, H
i
, D
i
Compartment i’s dimensions (width,
height and depth)
W Number of kiln cars
N Number of compartments in kiln car.
Y Number of different types of pieces.
S Number of different types of sets.
P Amount of orders.
V
iw
Volume of piece placed in the
compartment i of kiln car w.
P
iw
Weight of piece placed in the
compartment i in kiln car w.
W
iw
, H
iw
,
D
iw
Width, height and depth of piece placed
in the compartment i in kiln car w.
C
y
It is 0 if no piece of type y has been
loaded. Otherwise, it is 1.
AP
y
Average priority of piece y.
SAP
s
Average priority of requested set s.
X
yd
It is 1 if piece y belongs to product d.
Otherwise, it is 0
X
ds
It is 1 if product d belongs to set s.
Otherwise, it is 0
X
ps
It is 1 if order p is a set s’s order.
Otherwise, it is 0
X
iwy
It is 1 if piece y is placed in compartment
i in kiln car w. Otherwise, it is 0
RC
p
Amount requested in order p.
DD
p
Level of proximity of delivery date p.
Integer value between 1 to 5, with 5
being the closest one.
CP
p
Customer priority level of order p.
Integer value between 1 to 3, with 3
being the most important.
np
y
Amount of pieces of y-type taken into
account in the sum of priorities.
miss
y
Amount of pieces y pending to be kilned
in order to fulfil the orders.
maxMiss Maximum missing amount per piece
type.
Solutions generated must comply with the
following restrictions:
,∀∈
(8)
Implementation of a Memetic Algorithm to Optimize the Loading of Kilns for the Sanitary Ware Production
309
(9)
,
,
,
,
,
∀∈∀∈
(10)
,
,
,
,
,
∀∈∀∈
(11)
,
,
,
,
,
,
,
,
,
∀∈∀∈
(12)
1,∀∈,∀∈
(13)
,∀∈
(14)
Equations 8 and 9 constrain the weight to be borne
by a car and the total volume to be loaded into the
kiln. Equations 10, 11 and 12 indicate that the piece
must fit in the compartment it is placed. Equation 13
ensures that up to one piece is placed in each
compartment. Equation 14 checks that the amount of
pieces y allocated to the compartments do not exceed
the initial number of pieces y pending to be kilned.
The only constrains not considered in this paper
are baking time required per piece and color
combinations per selected group, which consist of not
allowing in a selection certain combination of colours
because the resulting pieces might not end up with the
expected colours. These constraints could be added in
future works.
5 NUMERIC
EXPERIMENTATION
The developed algorithm was compared to a genetic
algorithm, which takes as its starting point the same
initial population as the memetic one and uses the
same roulette method with binary search as selection
operator, as well as: crossover method, crossover rate
and stop conditions. With a slightly different
application of the mutation process where the number
of solutions to be mutated is a fixed proportion of the
population and the solutions selected are chosen with
the roulette method.
Before comparing them, the memetic (MA) and
genetic algorithms (GA) were calibrated in order to
get better results. In this process, real data about kiln,
kiln cars and products was used as well as 40 orders
lists that were generated randomly. Using each
combination of the parameter values, the algorithms
were applied to each of the order lists 40 times and
the average fitness for each combination was
calculated. As a result, the parameters were set on the
following values:
Table 2: Parameters values.
Stage Parameter MA GA
Crossover Crossover Rate 65% 65%
Crossover probability 70% 70%
Mutation Mutation rate 6% 7%
Local search Generation interval
(gLs)
1
Application rate
(probLS)
5%
Neighbors visited
(nLs)
100
Restoration /
Depuration
Percentage preserved 7% 10%
Alpha 0.4
The purpose of the comparison was to determine
which of them was the best suited for this type of
problems.
The data used in the comparison was extracted
from the results of 40 tests conducted with different
datasets. Each test was repeated 10 times for each
algorithm and based on this data the average value of
the algorithms’ performance was calculated.
Every test included the same type of sets, products
and pieces, changing only the orders’ files. We can
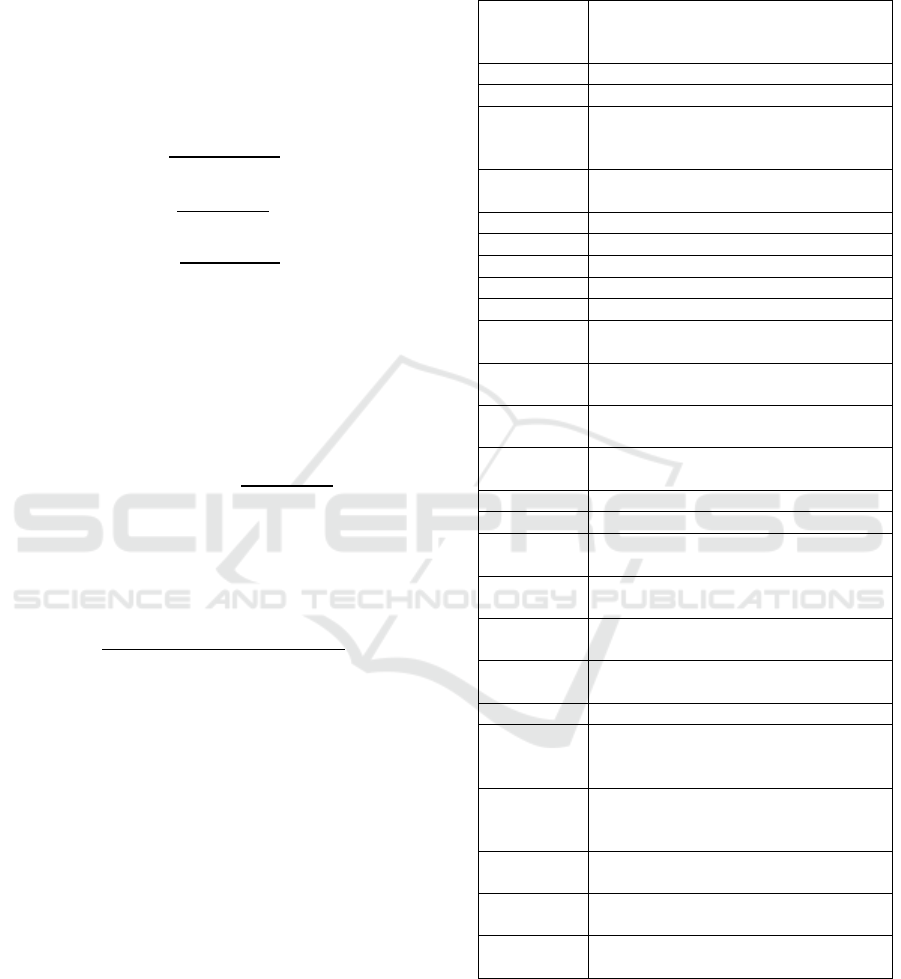
see fitness results on figure 4:
Figure 4: Fitness test results.
After conducting the ANOVA test, it was
determined that the difference between the two
algorithms was not significant, so that it was
concluded that both provide solutions of the same
quality level.
In addition, other tests were run changing the
amount of generations and the time to analyze the
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
310
behavior of the algorithm in two aspects (showed on
table 3 and 4 respectively):
How long do algorithms take to reach the 99%
of their optimum value?
Table 3: Average comparison values.
Memetic Genetic
Min Max Min Max
Generations 54.33 69.17 180.39 208.65
Time
(seconds)
29.40 32.37 105.29 121.26
How long does the genetic algorithm require to
reach the same performance than the memetic
one?
Table 4: Average comparison values.
Min Max
Generations 249.20 459.89
Seconds 176.22 312.99
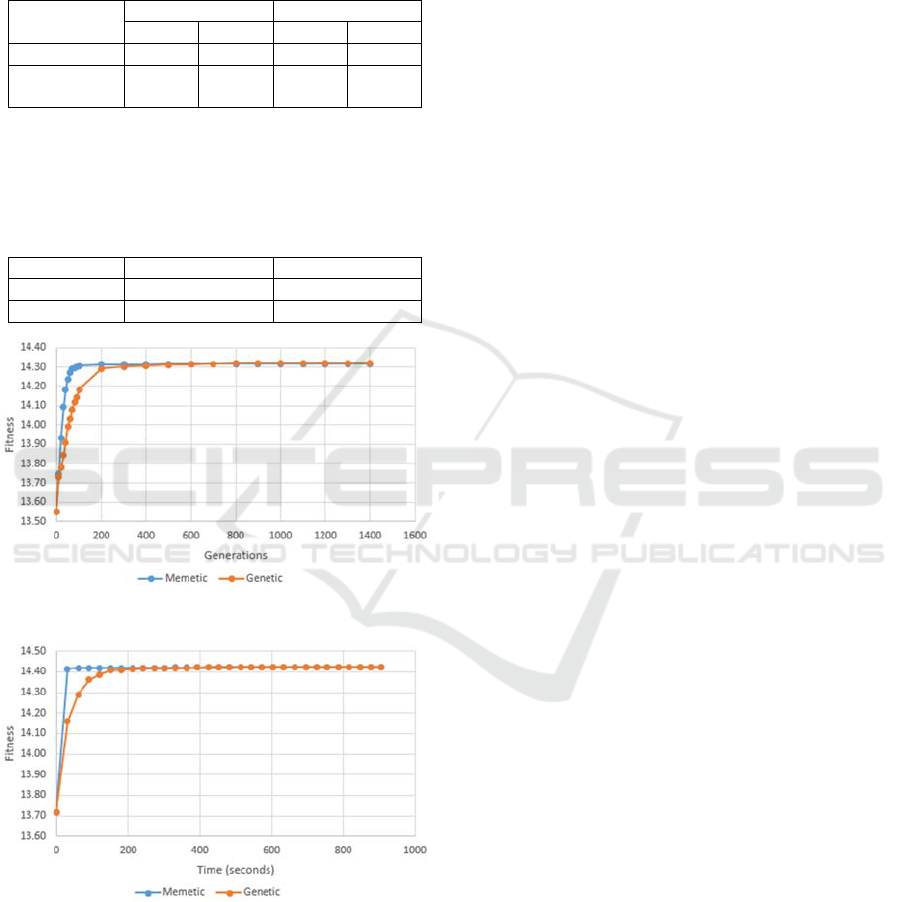
Figure 5: Behavior comparison by generations.
Figure 6: Behavior comparison by execution time.
6 CONCLUSIONS
A memetic algorithm was proposed as a method to
solve the selection of pieces issue in the firing stage
of the sanitary ware production. This algorithm was
chosen because of its similarities to the genetic one –
the most commonly used method for this type of
problems – and because it shows the same exploration
skills but a higher capacity of exploitation when
incorporating the local search.
After calibrating these algorithms to improve the
solutions generated, it was determined that the
difference between the solutions obtained for the
algorithm was not significant, so that we can conclude
that both provide solutions of the same quality level.
Additionally, it was found that the memetic
algorithm takes a smaller number of generations to
reach 99% of the optimum value while it requires a
shorter execution time than the genetic one. For this
reason, this method should be recommended to
sectors and industries where obtaining a good
solution in a short amount of time is vital.
In conclusion, this research offers a valid solution
for the pieces selection into the problem at sanitary
ware manufacturing industry. This solution is fast and
it’s adapted to the industry necessities and can be
applied in other fields where products composed of
several parts are manufactured and assembled. In
addition, this research takes into account multiple
factors related to demand such as client’s priority,
delivery dates and required amounts of products
while many others only consider a subset of this ones.
REFERENCES
Alba, E., & Dorronsoro, B., 2005. The
exploration/exploitation tradeoff in dynamic cellular
genetic algorithms. IEEE transactions on evolutionary
computation, 9(2), 126-142.
Baesler, F., & Palma, C., 2014. Multiobjective parallel
machine scheduling in the sawmill industry using
memetic algorithms. International Journal of Advanced
Manufacturing Technology, 74(5-8), 757-768.
Baiqing, Z., Haixing, L., Shaobu, B., Yifei, T., & Fei, H.,
2016. Study on the charging combination optimization
for forging production based on discrete shuffled frog
leaping algorithm. Mechanics, 22(5), 425-431.
Blum, C., & Roli, A., 2003. Metaheuristics in
combinatorial optimization: Overview and conceptual
comparison. ACM computing surveys (CSUR), 35(3),
268-308.
Ceramic Industry, 2015. Case Study: Collaborative Robots
in Technical Ceramic Parts Production.
Datoussaid, S., Verlinden, O., & Conti, C., 2002.
Application of Evolutionary Strategies to Optimal
Design of Multibody Systems. Multibody System
Dynamics, 8(4), 393-408.
Deb, K., 2004. Introduction to Genetic Algorithms for
Engineering Optimization. In New Optimization
Implementation of a Memetic Algorithm to Optimize the Loading of Kilns for the Sanitary Ware Production
311

Techniques in Engineering (pp. 13-51). Springer,
Berlín, Heidelberg.
Díaz, M., 2004. Estudio de información del proceso
productivo de la corporación Cerámica S.A.
Dorta, I., León, C., Rodríguez, C., Rodríguez, G., & Rojas,
A., 2003. Complejidad Algorítmica: de la Teoría a la
Práctica. In III Jornadas de Enseñanza Universitaria de
Informática.
Duda, J., & Stawowy, A., 2013. Optimization methods for
lot-sizing problem in an automated foundry. Archives
of Metallurgy and Materials, 58(3), 863-866.
Fuentes, A., Vélez, D., Moreno, S., Martínez, M., &
Sánchez, O., 2015. Problema de la mochila (Knapsack
problem). XIKUA Boletín Científico de la Escuela
Superior de Tlahuelilpan, 3(6).
Gómez Gutiérrez, C. (2010). Modelamiento y simulación
de un horno túnel industrial. Universidad Nacional de
Colombia, Medellín. Recuperado a partir de
http://www.bdigital.unal.edu.co/1882/1/71265369.201
0.pdf
Holland, J., 1992. Adaptation in Natural and Artificial
Systems: An Introductory Analysis with Aplications to
Biology, Control, and Artificial Intelligence. MIT
Press.
Ishibuchi, H., Tanigaki, Y., Akedo, N., & Nojima, Y., 2013.
How to strike a balance between local search and global
search in multiobjective memetic algorithms for
multiobjective 0/1 knapsack problems. In 2013 IEEE
Congress on Evolutionary Computation (pp. 1643-
1650).
Koblasa, F., Vavroušek, M., & Manlig, F. (2017). Three-
dimensional Bin Packing Problem with heterogeneous
batch constraints. In 35th International Conference
Mathematical Methods in Economics (pp. 330-335).
Hradec Králové: University of Hradec Králové.
Krasnogor, N., & Smith, J., 2005. A tutorial for competent
memetic algorithms: model, taxonomy and design
issues. IEEE Transactions on Evolutionary
Computation, 9(5), 474-488.
Leon, P., Cueva, R., Tupia, M., & Paiva Dias, G. (2019). A
Taboo-Search Algorithm for 3D-Binpacking Problem
in Containers. Advances in Intelligent Systems and
Computing, 930, 229-240. doi: DOI: 10.1007/978-3-
030-16181-1_22.
Lipowski, A., & Lipowska, D., 2012. Roulette-wheel
selection via stochastic acceptance. Physica A:
Statistical Mechanics and its Applications, 391(6),
2193-2196.
Liu, Y., Pan, Q., & Chai, T., 2015. Magnetic Material Group
Furnace Problem Modeling and the Specialization of the
Genetic Algorithm. IEEE Transactions on Engineering
Management, 62(1), 51-64.
Magalhaes-Mendes, J., 2013. A comparative study of
crossover operators for genetic algorithms to solve the
job shop scheduling problem. WSEAS transactions on
computers, 12
(4), 164-173.
Monzon, J., Cueva, R., Tupia, M., & Bruzza, M. (2019). A
cuckoo search algorithm for 2d-cutting problem in
decorative ceramic production lines with defects. In
11th International Conference on Agents and Artificial
Intelligence, ICAART 2019 (pp. 547-553). Prague:
Institute for Systems and Technologies of Information,
Control and Communication (INSTICC).
Moscato, P., & Cotta, C. (2003). An introduction to
memetic algorithms. Inteligencia Artificial, Revista
Iberoamericana de Inteligencia Artificial, 19, 131–148.
Porras, L. F. T (2018). Propuesta de mejora de una empresa
de producción de sanitarios y accesorios de baño en
Lima Metropolitana. Pontificia Universidad Católica
del Perú.
Regalado, E., Maroto, C., Ruiz, R, & García del Río B.
(2011). Análisis de la programación de la producción
en el sector cerámico español. Boletín de La Sociedad
Española de Cerámica y Vidrio, ISSN 0366-3175, Vol.
44, N
o
. 1, 2005, Pags. 39-44, 44.
Rhodes, D. (2004). Hornos para ceramistas. CEAC.
Savsar, M., & Abdulmalek, F. (2008). Modeling of a pull-
push assembly control system to minimize inventory
and demand delay costs. International Journal of
Industrial Engineering: Theory, Applications and
Practice, 15(1), 83–91.
Tupia, M., Cueva, R., & Guanira, M. (2017). A bat
algorithm for job scheduling in ceramics production
lines. In International Conference on Infocom
Technologies and Unmanned Systems: Trends and
Future Directions (ICTUS 2017) (pp. 266-270). Dubai:
IEEE.
Wang, K., Ma, W., Luo, H., & Qin, H., 2016. Coordinated
scheduling of production and transportation in a two-
stage assembly flowshop. International Journal of
Production Research, 54(22), 6891-6911.
Wrona, S., & Pawełczyk, M. (2013). Controllability-
Oriented Placement of Actuators for Active Noise-
Vibration Control of Rectangular Plates Using a
Memetic Algorithm. Archives of Acoustics, 38(4), 529–
536. https://doi.org/10.2478/aoa-2013-0062
Zhang, Q., Sun, X., & Wang, Z. (2009). An Efficient MA-
Based Materialized Views Selection Algorithm. 2009
IITA International Conference on Control, Automation
and Systems Engineering (Case 2009), 315–318.
https://doi.org/10.1109/CASE.2009.111
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
312
