A Hierarchical Convolution Neural Network Scheme for Radar Pulse

Detection

Van Long Do, Ha Phan Khanh Nguyen, Dat Thanh Ngo and Ha Quy Nguyen

Viettel High Technology Industries Corporation, Hoa Lac High-tech Park, Hanoi, Vietnam

Keywords:

Deep Learning, Hierarchical Neural Network, Radar Pulse Detection, Denoising Neural Network.

Abstract:

The detection of radar pulses plays a critical role in passive radar systems since it provides inputs for other

algorithms to localize and identify emitting targets. In this paper, we propose a hierarchical convolution

neural network (CNN) to detect narrowband radar pulses of various waveforms and pulse widths at different

noise levels. The scheme, named DeepIQ, takes a ﬁxed-length segment of raw IQ samples as inputs and

estimates the time of arrival (TOA) and the time of departure (TOD) of the radar pulse, if any, appearing

in the segment. The estimated TOAs and TODs are then combined across segments to form a sequential

detection mechanism. The DeepIQ scheme consists of sub-networks performing three different tasks: segment

classiﬁcation, denoising and edge detection. The proposed scheme is a full deep learning-based solution and

thus, does not require any noise ﬂoor estimation process, as opposed to the commonly used Threshold-based

Edge Detection (TED) methods. Simulation results show that the proposed solution signiﬁcantly outperforms

other schemes, especially under severe noise levels.

1 INTRODUCTION

In passive radar systems (Torrieri, 1984; Poisel,

2005), for example, Electronic Intelligence (ELINT)

or Early Warning System (EWS), the detection of

radar pulses is the process of estimating pairs of

the time of arrival (TOA) and the time of departure

(TOD) of the pulses from a sequence of received I/Q

samples. This task is essential for the location and

identiﬁcation of emitting sources. However, this is

not a trivial problem. Nowadays, radar signals are

very diversiﬁed with various modulation types and

pulse widths (Levanon and Mozeson, 2004; Richards,

2014; Pace, 2009). Moreover, in severe conditions

with low Signal–to–Noise Ratio (SNR) level, most of

radar pulses are buried in noise. Therefore, it is very

difﬁcult to detect the presence of true radar pulses in

such noisy environments.

In recent years, Deep Learning (LeCun et al.,

2015; Goodfellow et al., 2016) has emerged as

a powerful tool for many tasks in computer vi-

sion and image processing such as image classiﬁca-

tion (Krizhevsky et al., 2012; Szegedy et al., 2015; He

et al., 2016), denoising and image restoration (Zhang

et al., 2017; Mao et al., 2016), and object detec-

tion (Ren et al., 2017; Redmon et al., 2016; Liu et al.,

2016). Inspired by these successes, in this paper, we

focus on designing a full deep learning-based scheme,

named DeepIQ, for radar pulse detection. In this

method, the received radar signal is ﬁrst divided into

overlapping ﬁxed-length segments, each of which is

then fed to a hierarchical convolutional neural net-

work to estimate the TOA and/or TOD, if any. By

using sufﬁciently small segments, we can safely as-

sume that each segment contains at most one radar

pulse. The TOA and TOD estimates obtained from

DeepIQ are tracked and updated, if necessary, after

each segment is processed.

The contribution of this paper is as follows:

• We present a novel neural network structure,

called Classiﬁcation Net to determine whether a

radar pulse appears in the segment. By using

deep-learning based approach, we get rid of noise

ﬂoor estimation process for setting the detection

threshold as in previous works.

• We design a denoising neural network, named De-

noising Net to mitigate the noise effect on re-

ceived radar signal and thus improve signiﬁcantly

the detection accuracy.

• We propose a neural network architecture, named

Edge-Detection Net, which contains three differ-

ent nets (TOA Net, TOD Net and TOA-TOD Net)

with the same architecture to estimate the TOA

Do, V., Nguyen, H., Ngo, D. and Nguyen, H.

A Hierarchical Convolution Neural Network Scheme for Radar Pulse Detection.

DOI: 10.5220/0008876500150022

In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 15-22

ISBN: 978-989-758-397-1; ISSN: 2184-4313

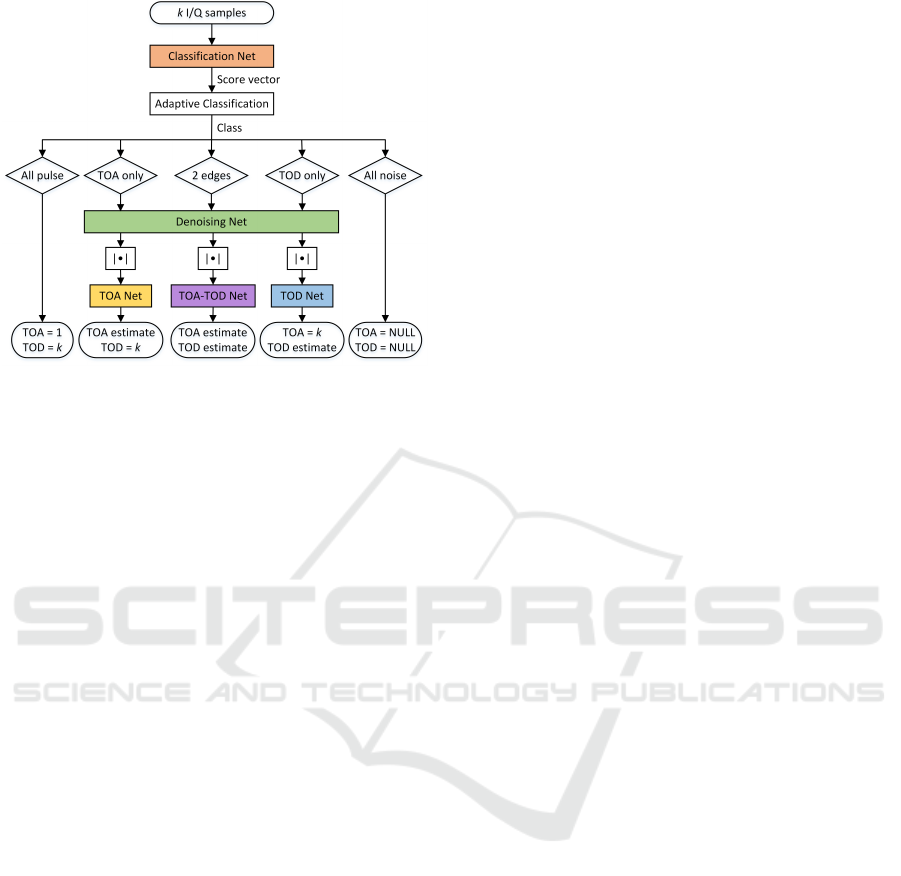
Figure 1: Flowchart of the DeepIQ network.

and/or TOD from the received radar signal de-

pending on the result of the Classiﬁcation Net.

• We conduct extensive simulations to evaluate the

effectiveness of our proposed scheme. The simu-

lation results indicate that DeepIQ improves sig-

niﬁcantly the radar pulse detection accuracy.

Figure 1 depicts the overview of the DeepIQ

scheme. The proposed method receives a segment

of k I/Q samples and estimates the TOA and TOD

of radar pulses. Our proposed CNN blocks are high-

lighted in colored. The symbol | · | denotes the modu-

lus operator.

The rest of this paper is organized as follows. We

ﬁrst review the related studies in Section II. In Sec-

tion III, we describe necessary assumptions and for-

mally deﬁne the problem. The detail of our proposed

scheme is shown in Section IV. We show simulation

results in Section V. Finally, the conclusion is pre-

sented in Section VI.

2 RELATED WORK

Since radar pulse detection is an important opera-

tion in Electronic Warfare systems such as ELINT or

EWS, there are many studies on this problem in re-

cent years. In (Torrieri, 1974; Iglesias et al., 2014),

the authors proposed an adaptive thresholding scheme

to detect and estimate the TOA and TOD of radar

pulses. Albaker et al. (Albaker and Rahim, 2011) ap-

plied a dual threshold noise gate subsystem to ex-

tract the parameters of radar pulses. The authors

in (Lakshmi et al., 2013) proposed a model for de-

tection and extraction of pulse parameters in Radar

Warning Receivers. In their model, the TOA and

TOD are estimated by a predeﬁned hard threshold.

In (Lancon et al., 1996), the radar signal is extracted

using a correlation method that takes advantage of

the periodic characteristic of radar signals. In this

method, a detection threshold is selected to determine

the correlation peak based on the noise statistic. To

the best of our knowledge, all of the aforementioned

schemes for radar pulse detection are threshold-based,

in which the thresholds are deﬁned through estimat-

ing the noise statistics. These methods yield good

performances under high or moderate SNR levels but

fail under low SNR levels. Moreover, the noise ﬂoor

estimation–an essence of these algorithms–is itself a

non-trivial task, especially in quickly varying envi-

ronments.

In our previous work (Nguyen et al., 2019), we

introduced a deep learning based framework to solve

radar pulse detection problem. The method consists

of two steps. In the ﬁrst step, a CNN is trained to

determine whether a pulse or part of a pulse appears

in a segment of the signal. In the second step, TOA

and TOD of radar pulses are estimated by ﬁnding the

change points in the segment via Pruned Exact Lin-

ear Time (PELT) method (Killick et al., 2012). Al-

though this method improved signiﬁcantly the radar

pulse detection performance in comparison with other

TED methods, it retains drawbacks. Firstly, since the

TOA and TOD parameters are found in the second

step by solving an optimization problem using classi-

cal ﬁnd–change–point algorithms, the previously pro-

posed scheme is not a full deep learning approach.

Secondly, its performance still is degraded remark-

ably in noisy conditions with very low SNR level.

These shortcomings motivate us to propose a novel

scheme that is a full deep learning solution and more

resilient to noise. It will be shown that the hierarchi-

cal convolution neural network scheme proposed in

this paper outperforms previous radar pulse detectors,

especially in low SNR conditions.

3 PRELIMINARIES

Considering throughout this paper a narrowband radar

signals that are sampled at 78.125 Msps and centered

around frequency 0. What we receive is a complex-

valued (or I/Q) signal that is corrupted by an Additive

White Gaussian Noise (AWGN):

ˆx[n] = x[n] + w[n], n ∈ Z, (1)

where x is a train of rectangular pulses and w is the

AWGN. Assuming Nyquist’s sampling, each sample

of the discrete-time signal corresponds to a period of

12.8 ns. The pulses are of various waveforms and

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

pulse widths. This work considers 7 types of modula-

tions commonly used in modern radar systems (Lev-

anon and Mozeson, 2004; Richards, 2014; Pace,

2009): Continuous Waveform (CW), Step Frequency

Modulation (SFM), Linear Frequency Modulation

(LFM), Non-Linear Frequency Modulation (NLFM),

Costas code (COSTAS), Barker code (BARKER), and

Frank code (FRANK). Assuming furthermore that all

pulses are modulated in the basedband over a band-

width of 20 MHz. The pulse widths largely vary from

0.1 to 400 µs, which corresponds to a range from 8

to 31250 samples. To reduce the effect of noise, the

received signal ˆx is lowpass-ﬁltered with ﬁlter h of

bandwidth 20 MHz that results in:

ˆx

= h ∗ ˆx = h ∗ x + h ∗ w =: x

+ w

, (2)

where x

is a smoothed version of the pulse train and

is colored Gaussian noise.

The location of each pulse is characterized by the

TOA (the middle of the rising edge) and the TOD (the

middle of the falling edge). Our goal is to estimate the

series of TOAs and TODs by looking at consecutive

(overlapping) length–k segment of ˆx

, one at a time.

In practice, the radar pulses in a narrowband are well

separated in time and so, we can choose k such that at

most one pulse is within a segment. From now on, let

us assume that the minimum distance between con-

secutive pulses is 2000 samples and therefore choose

k = 2000. For each segment, if a pulse or a part of

it appears, DeepIQ outputs a pair of TOA and TOD

in terms of sample indices; otherwise it decides that

the whole segment is just noise and set both TOA and

TOD to null. Note that if a rising edge is missing,

TOA is set to 1; if a falling edge is missing, TOD

is set to k. The whole process is achieved by train-

ing 5 CNNs separately and attaching them together as

shown in Figure 1. A list of detected pulses is kept;

when a new pulse is detected, it will be merged to the

right previous pulse if the distance between them is

negligible.

4 PROPOSED SCHEME

In this section, we describe in detail the architecture

of the DeepIQ network which consists of ﬁve sub-

networks, namely Classiﬁcation Net, Denoising Net,

and three Edge-Detection Nets.

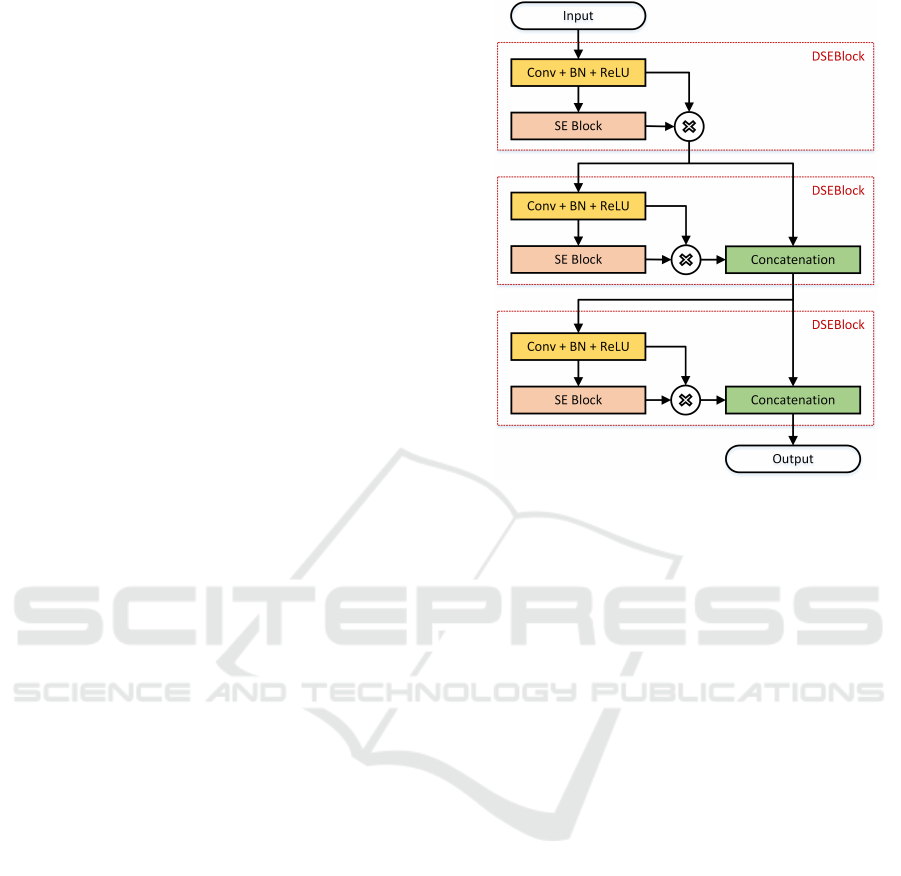
In all of them, we introduce the Dense Squeeze-

and-Excitation Block (DSEBlock) that is a combina-

tion of a DenseBlock (Huang et al., 2017) with the

Squeeze-and-Excitation (SE) mechanism (Hu et al.,

2018). The DenseBlock enhances the gradient ﬂow

in the network and encourages feature reuse, while

Figure 2: Architecture of DSEBlock-3. DSEBlock-4 and

DSEBlock-5 are obtained by repeating the dashed block

once or twice more, respectively.

the SE re-weights the feature maps for better feature

learning. In a DSEBlock-n, the input is ﬁrst fed to

a composite function consisting of a convolution fol-

lowed by a Batch Normalization (Ioffe and Szegedy,

2015) and then followed by a Rectiﬁed Linear Unit

(ReLU). The result is then passed to and also gated by

an SE block, whose architecture is described in (Hu

et al., 2018). This process is repeated n times with

skip connections to form a densely connected net-

work. For example, the architecture of DSEBlock-3

is shown in Figure 2.

4.1 Classiﬁcation Net

By assuming that each segment of 2,000 I/Q samples

can contain at most one pulse, we design the Classi-

ﬁcation Net to classify a segment into one of the ﬁve

categories:

• ‘2 edges’: both TOA and TOD of a pulse appear

in the segment.

• ‘TOA only’: a TOA appears in the segment with-

out TOD.

• ‘TOD only’: a TOD appears in the segment with-

out TOA.

• ‘All pulse’: the whole segment is a part of a pulse.

• ‘All noise’: the segment contains only background

noise.

A Hierarchical Convolution Neural Network Scheme for Radar Pulse Detection

(a) 2 edges

(b) TOA only (c) TOD only

(d) All pulse (e) All noise

Figure 3: The 5 classes of segments of the signal envelop

for SNR = 6 dB at bandwidth 20 MHz.

Figure 3 depicts these classes under a relatively low–

SNR level.

The architecture of the Classiﬁcation Net is shown

in Figure 4. This network consists of a DSEBlock-3

followed by a single ﬁlter of size 1 × 3, a Dropout

layer with dropping ratio of 0.5 and 4 fully connected

(FC) layers of size 128, 128, 128 and 5, respectively.

The ﬁrst three FC layers use the ReLU activation

function, while the last FC layer is attached to a soft-

max function to output a score vector of length 5. In

each convolution layer of the DSEBlock-3, we use 16

ﬁlters of size 1 × 3.

Figure 4: Architecture of the Classiﬁcation Net.

Each segment s of the signal ˆx

is treated as a 1-

D signal with two channels: channel-I (real part) and

channel-Q (imaginary part). Before feeding the seg-

ment to the Classiﬁcation Net, we normalize it ac-

cording to:

norm

[n] =

s[n]

max

max{|s

[i]|, |s

[i]|}

, ∀n. (3)

The cross-entropy loss function is used to train the

network. To decide the label of a segment, we in-

corporate the score vector output by the Classiﬁcation

Net to an adaptive classiﬁcation. This procedure takes

into account the following observations:(1) ‘2 edges’

cannot be followed by ‘All pulse’; (2) ‘TOA only’

cannot be followed by ‘All noise’; (3) ‘TOD only’

cannot be followed by ‘All pulse’; (4) ‘All pulse’ must

be followed by ‘TOD only’ or ‘All pulse’ and (5) ‘All

noise’ cannot be followed by ‘TOD only’ and ‘All

pulse’. Therefore, the main idea of the adaptive clas-

siﬁcation is that we exclude impossible labels from

the score vector of the current segment based on the

label of the previous one, if its conﬁdence was high;

then take argument max of the rest as the label and its

score as the conﬁdence of the current segment. This

is repeated until the end of the signal.

4.2 Denoising Net

We adopt a residual learning strategy (Zhang et al.,

2017) for the Denoising Net. The input of the network

is a noisy I/Q segment that includes a TOA and/or

a TOD and the output is a perturbation of the same

size that will be subtracted from the input to compen-

sate for the noise. The network is trained to minimize

the mean squared error between the output and the

ground-truth noise, which is a segment of w

given in

(2).

The architecture of the Denoising Net is sketched

in Figure 5. It incorporates DSEBlocks into an

encoder-decoder network with symmetric skip con-

nections (Mao et al., 2016) in the same spirit as (J

egou

et al., 2017). Here, we use ﬁve DSEBlock-5, each of

which is followed by a 1 × 1 convolution layer to re-

duce the number of feature maps by a factor of 5. In-

side a DSEBlock-5, the number of ﬁlters used in the 5

convolution layers are 32, 48, 64, 80 and 96, respec-

tively; all ﬁlters are of size 1 × 7. The Downsampling

is simply a 1 × 2 max pooling. The Upsampling is a

1 × 7 transposed convolution with stride 2.

4.3 Edge-detection Nets

To locate the edges in a segment, the magnitude of

the output of Denoising Net is passed to one of three

Edge–Detection Nets: TOA Net, TOD Net and TOA-

TOD Net. Which network is used depends on the re-

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

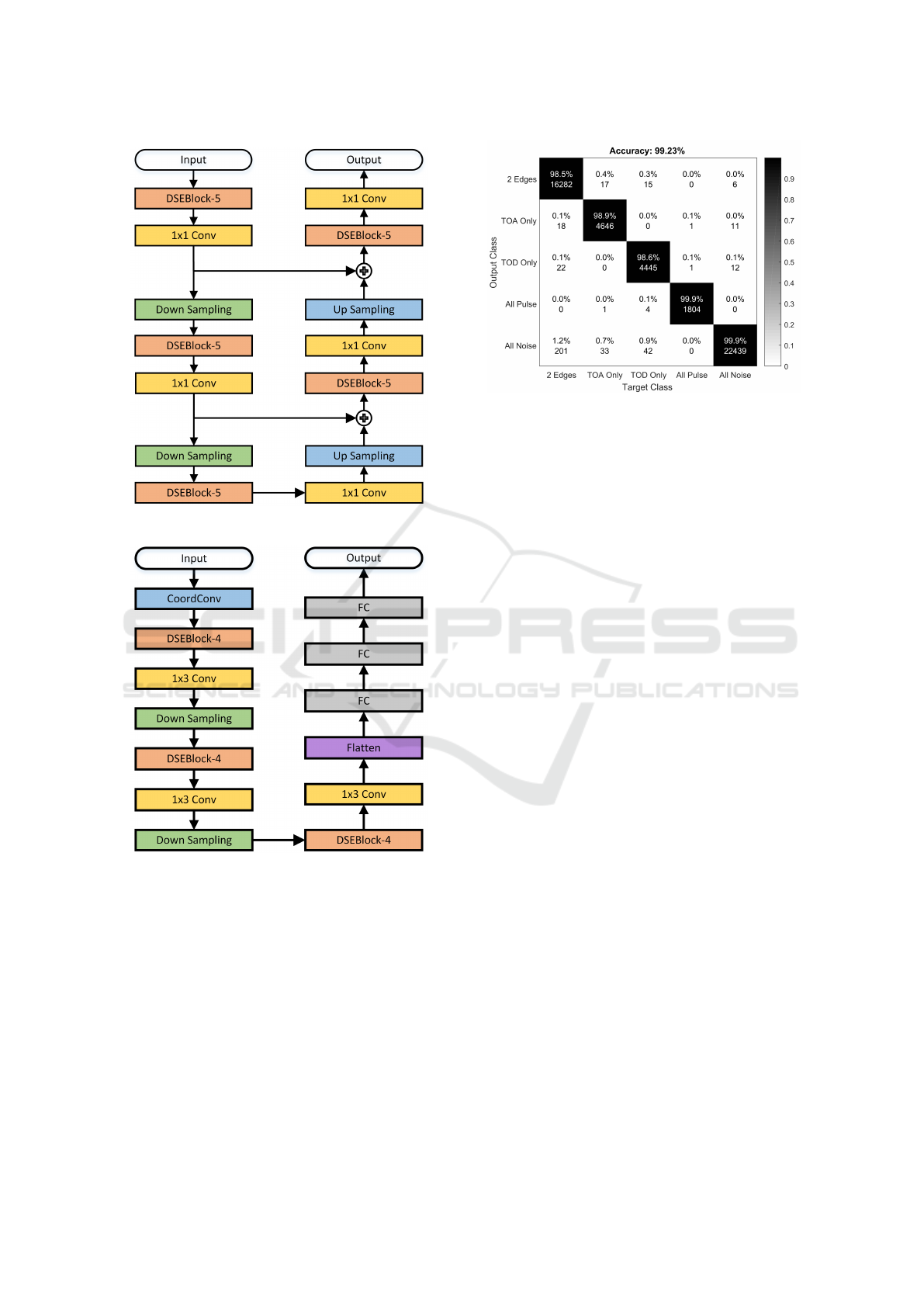
Figure 5: Architectures of the Denoising Net.

Figure 6: Architecture of the Edge Detection Nets (TOA

Net, TOD Net, and TOA-TOD Net). The output of TOA

Net or TOD Net is a scalar, whereas the output of TOA-

TOD Net is a two-dimension vector.

sult of the segment classiﬁcation, as shown in Fig-

ure 1. These three networks share the same architec-

ture as depicted in Figure 6 but are trained separately

on different datasets. The Coordinate-Convolution

(CoordConv) layer (Liu et al., 2018) simply maps the

coordinates of all samples in the segment to an ar-

ray in [−1, 1] and then appends it to the input as a

new channel. This is to incorporate the location in-

formation into the learning for better edge detection.

The result is then passed to a concatenation of three

Figure 7: Confusion matrix of Classiﬁcation Net on the test

set.

DSEBlock-4, each of which is followed by a 1 × 3

convolution layer that reduces the number of feature

maps by a factor of 4. The ﬁrst two of them are fur-

ther attached to a Downsampling that is a 1 × 2 max

pooling. We use 16, 8 and 4 ﬁlters in each convolu-

tion layer of the ﬁrst, second, and third DSEBlock-4,

respectively; all ﬁlters are of size 1 × 3.

The tail of the network is a concatenation of 3 FC

layers: the ﬁrst two layers are of size 128 and the last

one is of size 1 (for TOA Net and TOD Net) or 2 (for

TOA-TOD Net). By using the sigmoid function in the

end, the outputs of edge-detection nets are always in

[0, 1]. Each network is trained to minimize the Mean

Absolute Error (MAE) between output and ground-

truth TOA and/or TOD, which are also normalized to

[0, 1].

5 PERFORMANCE EVALUATION

In this section, we provide some results for simulated

radar pulses. All data were generated by a simula-

tor written in Matlab. The training of proposed sub-

networks was implemented in Python with Keras li-

brary and TensorFlow backend running on 4 Nvidia

Tesla P100 GPUs. The training data for all networks

are segments of 2,000 I/Q samples, each of which is

randomly truncated from a longer signal that contains

a rectangular radar pulse. Each pulse was randomly

generated with one of the seven aforementioned mod-

ulation types, over a pulse width in [0.1, 400] µs and

with an SNR (over the 20 MHz bandwidth) in [0, 15]

dB. All sub-networks were trained for 100 epochs us-

ing an Adam optimizer with a learning rate of 10

−4

and the best models are selected for DeepIQ.

Firstly, the Classiﬁcation Net was trained on

1,000,000 examples labeled with ﬁve categories: ‘2

A Hierarchical Convolution Neural Network Scheme for Radar Pulse Detection

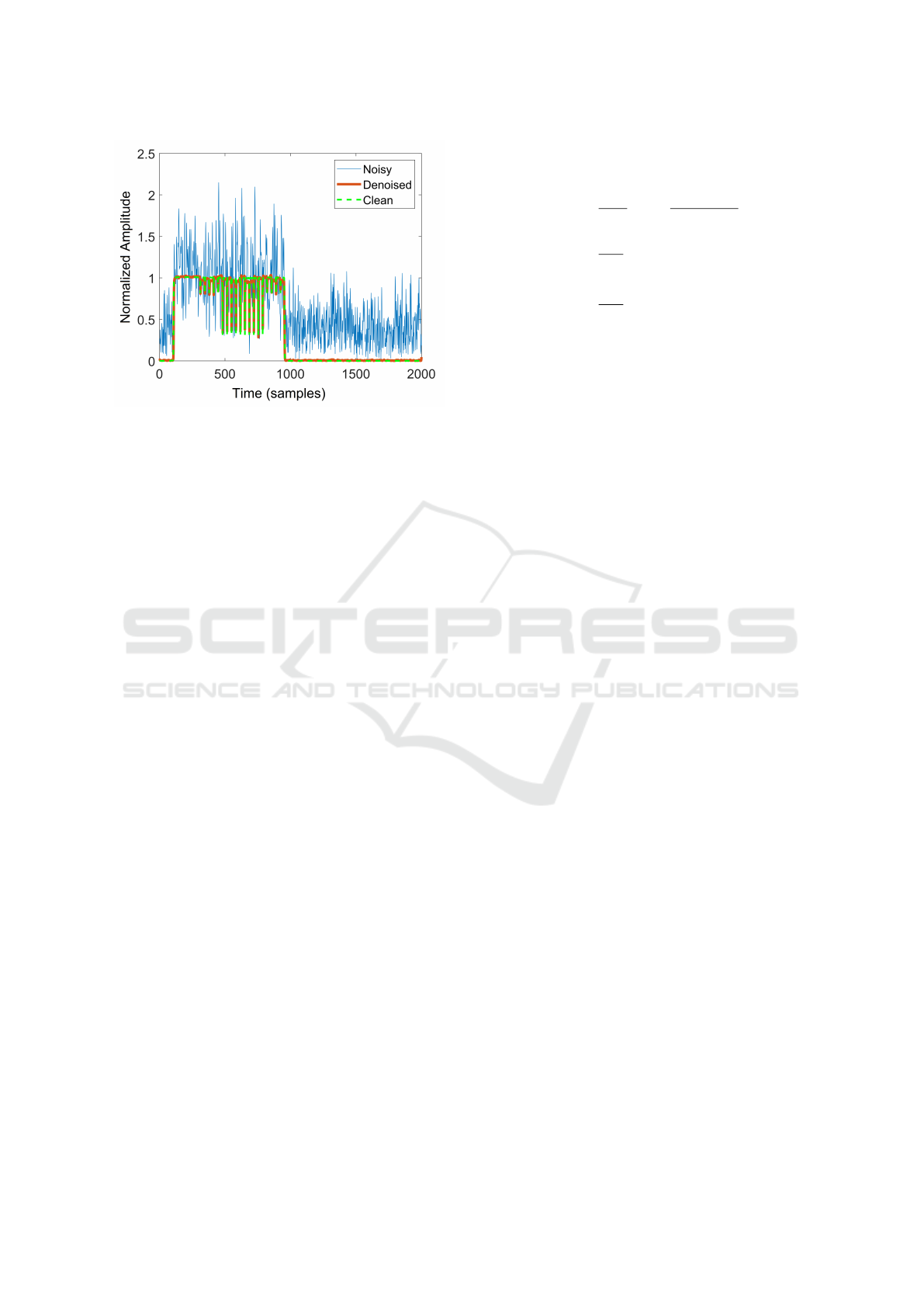
Figure 8: An example of denoising of a modulated radar

pulse.

edges’, ‘TOA only’, ‘TOD only’, ‘All pulse’ and ‘All

noise’. The best model was tested on another sepa-

rated set of 50,000 examples, yielding an overall ac-

curacy of 99.23% with the confusion matrix shown in

Figure 7. Secondly, the Denoising Net was trained on

500,000 segments of the ﬁrst three labels. The result-

ing model was able to improve the average SNR of

150, 000 testing examples by 22.43 dB. Figure 8 vi-

sualizes the denoising of an example received noisy

radar pulse. Finally, the TOA Net, TOD Net and

TOA-TOD Net were trained on three different sets,

each of which includes the envelops of 500, 000 sam-

ples of denoised segments with labels ‘TOA only’,

‘TOD only’ and ‘2 edges’, respectively. These net-

works achieved the MAEs of 26.38 ns, 26.45 ns and

27.67 ns on average, respectively, over separated test

sets of 150,000 samples each. To test the whole detec-

tion procedure, we run DeepIQ scheme on segments

of a long signal containing N

true

= 10, 000 pulses

equally separated by 6, 000 samples under different

SNR levels. Two pulses output by DeepIQ are merged

into one if the distance between them is less than 25

µs. Then, we evaluate the performance of the pro-

posed DeepIQ network in both detection and estima-

tion metrics.

Let us denote the list of ground-truth TOAs and

TODs by {(a

, d

)}

true

i=1

and the list of estimated TOAs

and TODs by {( ˆa

)}

est

i=1

. A pulse (a

, d

) is called

detected if there exists j ∈ {1, 2, . . . , N

est

} such that:

− ˆa

| < 200 ns. (4)

By renumbering, assuming that the detected pulses

{(a

, d

)}

det

i=1

are matched by the subset {( ˆa

)}

det

i=1

of estimated pulses. The remaining pulses,

{( ˆa

)}

est

i=N

det

, are considered false alarms. The

detection performance is then measured by the fol-

lowing four metrics: the detection rate, the F1 score,

the TOA Mean Absolute Error (MAE) and and the

TOD MAE, which are computed as:

det

true

, F

det

true

+ N

est

∆

TOA

det

∑

i=1

− ˆa

∆

TOD

det

∑

i=1

−

Note that the detection rate measures the sensitivity

of the algorithm while the F1 score balances the true

detection rate and the false alarm rate.

To evaluate the performance of our proposed

scheme in this paper, we compare the detection accu-

racy of DeepIQ with that of the Threshold-based Edge

Detection (TED) algorithm (Iglesias et al., 2014) and

our previous work based on Find–Change–Points al-

gorithms (FCA) (Nguyen et al., 2019). Table 1 reports

the detection performances of three methods for vari-

ous SNR levels from 0 dB to 15 dB. It can be seen that

DeepIQ achieves the superior performance compared

with TED and FCA in all measures and for all SNR

levels. Especially, the performance gaps are strikingly

much larger in low-SNR regimes. For example, in the

extremely noisy case when SNR = 0 dB, the proposed

scheme DeepIQ is able to boost the F1 score from

1.59% of TED and 32.72% of FCA to 55.57%. Fur-

thermore, DeepIQ achieves a reduction of 38 ns and

22 ns in the TOA MAE as compared with TED and

FCA. The TOD MAE of DeepIQ is also 27.15 and

6.74 times smaller than that of TED and FCA, respec-

tively.

Our proposed scheme DeepIQ is a better solution

to solve the radar pulse detection compared with pre-

vious schemes because of the following underlying

reasons:

• Firstly, noise ﬂoor estimation is a prerequisite in

previous TED schemes in order to determine de-

tection threshold. However, in low–SNR levels,

accuracy estimation of detection threshold is a

very difﬁcult task due to the effect of noise. Im-

proper detection threshold leads to a signiﬁcant

degradation of radar pulse detection, for e.g. high

false alarm and missed detection rates. Thanks

to the proposed classiﬁcation neural network with

deep-learning approach which reduces the tedious

detection threshold setting, DeepIQ reaches a bet-

ter detection if a radar pulse is present, partially

present of absent in the received signal.

• Secondly, previous methods including our pre-

vious work apply traditional algorithms such as

threshold based algorithm (TED) or ﬁnd-change-

point algorithm (FCA) to estimate the TOA and

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods

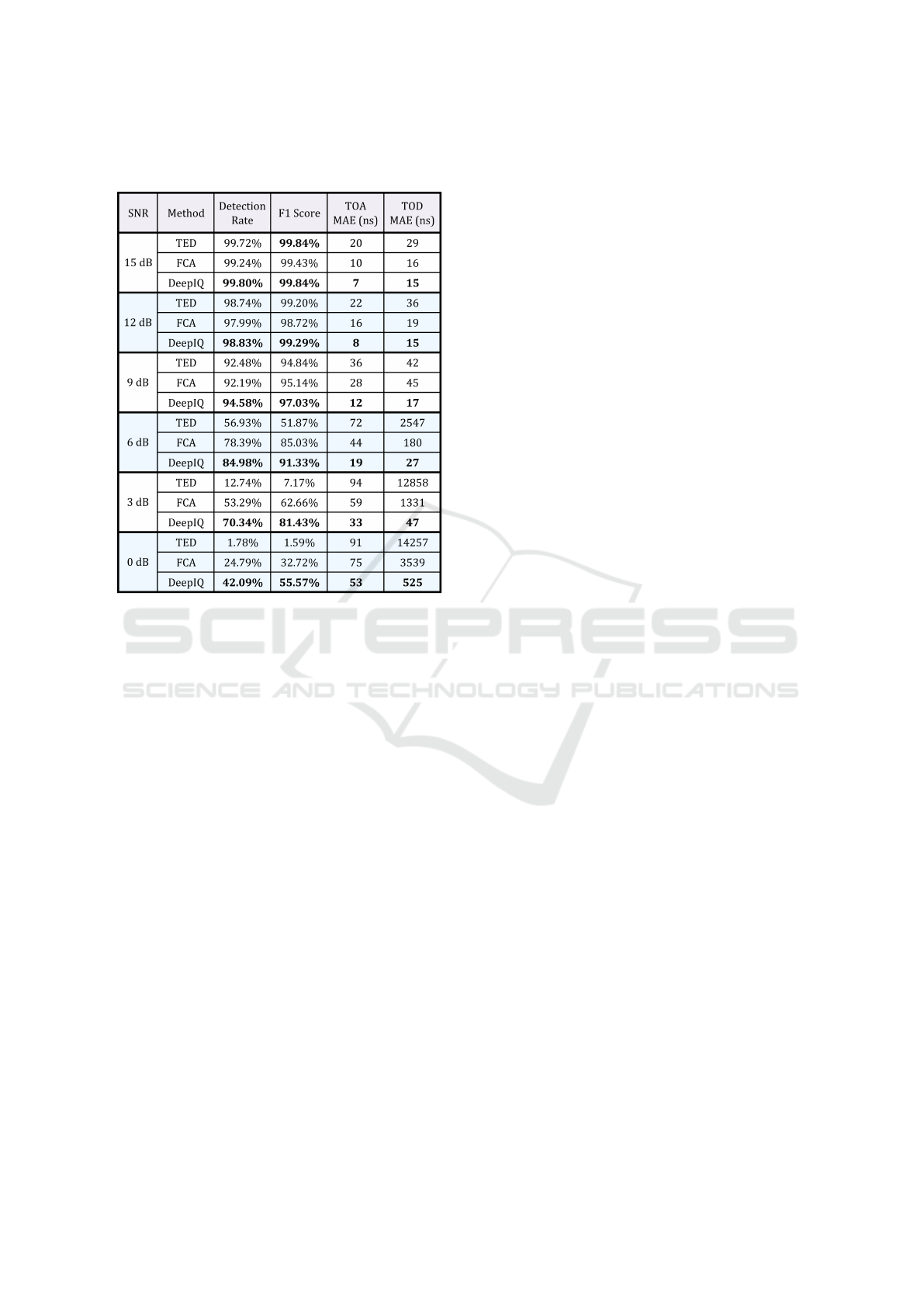
Table 1: Performance comparison of schemes with different

SNR levels at the bandwidth of 20 MHz.

TOD positions in the edges of radar pulse. The

drawback of these approaches is the edges of radar

pulse are deformed critically under the effect of

noise in low–SNR levels. Therefore, it is very dif-

ﬁcult to estimate correctly in such conditions. By

applying the state-of-the art techniques in the pro-

posed Denoising Net and Edge–Detection Nets,

DeepIQ can mitigate the effect of noise as well

as achieve a signiﬁcant improvement of detection

accuracy in severe conditions.

6 CONCLUSION

In this paper, we have introduced a hierarchical con-

volution neural network scheme, DeepIQ, for the de-

tection of radar pulses with various waveforms over

a wide range of SNR levels. The proposed scheme

is obtained by assembling 5 sub-convolution neural

network that are in charge of 3 different roles: clas-

siﬁcation, denoising, and edge detection. These net-

works are trained on radar I/Q segments of a ﬁxed

length. The simulation results show that DeepIQ sig-

niﬁcantly outperforms the Threshold-based Edge De-

tection (TED) scheme (Iglesias et al., 2014) and our

previous work (Nguyen et al., 2019) especially for

low SNR levels. The shortcoming of our method is

its computation time, about 0.44 µs/sample on one

GPU, which is still far from the real-time target,

12.8 ns/sample. Future work should focus on com-

pressing DeepIQ’s sub-networks as suggested in (Han

et al., 2016).

REFERENCES

Albaker, B. M. and Rahim, N. A. (2011). Detection and pa-

rameters interception of a radar pulse signal based on

interrupt driven algorithm. Int. Conf. on Emerging Re-

search in Computing, Information, Communications

and Applications (ERCICA), 6:1380–1387.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Han, S., Mao, H., and Dally, W. J. (May 02-04, 2016).

Deep compression: Compressing deep neural net-

works with pruning, trained quantization and huffman

coding. In Proc. Int. Conf. Learning Representations

(ICLR), pages 1–14, Puerto Rico.

He, K., Zhang, X., Ren, S., and Sun, J. (Jun. 27-30, 2016).

Deep residual learning for image recognition. In Proc.

Conf. Comput. Vis. Pattern Recogn. (CVPR), pages

770–778, Las Vegas, NV, USA.

Hu, J., Shen, L., and Sun, . (June 18-22, 2018). Squeeze-

and-Excitation networks. In Proc. Conf. Comput. Vis.

Pattern Recogn. (CVPR), pages 7132–7141, Salt Lake

City, UT, USA.

Huang, G., Liu, Z., van der Maaten, L., and Weinberger,

K. Q. (July 21-26, 2017). Densely connected convo-

lutional networks. In Proc. Conf. Comput. Vis. Pat-

tern Recogn. (CVPR), pages 4700–4708, Honolulu,

HI, USA.

Iglesias, V., Grajal, J., Yeste-Ojeda, O., Garrido, M.,

anchez, M. A., and L

opez-Vallejo, M. (May 19-23,

2014). Real-time radar pulse parameter extractor. In

Proc. IEEE Radar Conf., pages 1–5.

Ioffe, S. and Szegedy, C. (Jul. 06-11, 2015). Batch nor-

malization: Accelerating deep network training by re-

ducing internal covariate shift. In Proc. Int. Conf.

Machine Learning (ICML), pages 1097–1105, Lille,

France.

egou, S., Drozdzal, M., Vazquez, D., Romero, A., and Ben-

gio, Y. (2017). The one hundred layers tiramisu: Fully

convolutional DenseNets for semantic segmentation.

arXiv:1611.09326 [cs.CV].

Killick, R., Fearnhead, P., and Eckley, I. A. (2012). Optimal

detection of changepoints with linear computational

cost. J. Am. Stat. Assoc., 107(500):1590–1598.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (Dec. 03-

08, 2012). Imagenet classiﬁcation with deep convo-

lutional neural networks. In Proc. Adv. Neural Inf.

Process. Syst. (NIPS), pages 1097–1105, Lake Tahoe,

NV, USA.

Lakshmi, G., Gopalakrishnan, R., and Kounte, M. R.

(2013). Detection and extraction of radio frequency

and pulse parameters in radar warning receivers. In

Scientiﬁc Research and Essays, pages 632–638.

A Hierarchical Convolution Neural Network Scheme for Radar Pulse Detection

Lancon, F., Hillion, A., and Saoudi, S. (1996). Radar sig-

nal extraction using correlation. In European Signal

Processing Conf. (EUSIPCO), pages 632–638.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. Nature, 521:436–444.

Levanon, N. and Mozeson, E. (2004). Radar Signals.

Wiley-Interscience.

Liu, R., Lehman, J., Molino, P., and Such, F. P. (2018).

An intriguing failing of convolutional neural net-

works and the CoordConv solution. arXiv:1807.03247

[cs.CV].

Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S.,

Fu, C.-Y., and Berg, A. C. (Oct. 08-16, 2016). SSD:

Single shot multibox detector. In Proc. Eur. Conf.

Comput. Vis. (ECCV), pages 21–37, Amsterdam, The

Netherlands.

Mao, X.-J., Shen, C., and Yang, Y.-B. (Dec. 05-10,

2016). Image restoration using very deep convolu-

tional encoder-decoder networks with symmetric skip

connections. In Proc. Adv. Neural Inf. Process. Syst.

(NIPS), pages 1–9, Barcelona, Spain.

Nguyen, H. Q., Ngo, D. T., and Do, V. L. (2019). Deep

learning for radar pulse detection. In Int. Conf.

on Pattern Recognition Applications and Methods

(ICPRAM), pages 32–39.

Pace, P. E. (2009). Detecting and Classifying Low Proba-

bility of Intercept Radar. Artech House, 2 edition.

Poisel, R. (2005). EW Target Location Methods. Artech

House.

Redmon, J., Divvala, S., Girshick, R., and Farhadi, A. (Jun.

27-30, 2016). You Only Look Once: Uniﬁed, real-

time object detection. In Proc. Conf. Comput. Vis. Pat-

tern Recogn. (CVPR), pages 779–788, Las Vegas, NV,

USA.

Ren, S., He, K., Girshick, R., and Sun, J. (2017). Faster

R-CNN: Towards real-time object detection with re-

gion proposal networks. IEEE Trans. Pattern Anal.

Machine Intell., 39(6):1137–1149.

Richards, M. A. (2014). Fundamental of Radar Signal Pro-

cessing. McGraw-Hill Education, 2 edition.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (Jun. 07-12, 2015). Going deeper with

convolutions. In Proc. Conf. Comput. Vis. Pattern

Recogn. (CVPR), pages 1–9, Boston, MA, USA.

Torrieri, D. J. (1974). Arrival time estimation by adaptive

thresholding. IEEE Trans. Aerospace Electro. Sys-

tems, AES-10(2):178–184.

Torrieri, D. J. (1984). Statistical theory of passive location

systems. IEEE Trans. Aerospace Electro. Systems,

AES-20(2):183–198.

Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L.

(2017). Beyond a Gaussian denoiser: Residual learn-

ing of deep CNN for image denoising. IEEE Trans.

Image Process., 26(7):3142–3155.

ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods