
On Idle Energy Consumption Minimization in Production:
Industrial Example and Mathematical Model
Ond
ˇ
rej Benedikt
1,2 a
, P
ˇ
remysl
ˇ
S
˚
ucha
1 b
and Zden
ˇ
ek Hanz
´
alek
1 c
1
Czech Institute of Informatics, Robotics and Cybernetics, Czech Technical University in Prague,
Jugosl
´
avsk
´
ych partyz
´
an
˚
u 1580/3, Prague, Czech Republic
2
Czech Technical University in Prague, Faculty of Electrical Engineering, Department of Control Engineering,
Karlovo n
´
am
ˇ
est
´
ı 13, Prague, Czech Republic
Keywords:
Scheduling, Energy Optimization, Operation Modes, Mixed Integer Linear Programming, Parallel Machines.
Abstract:
This paper, inspired by a real production process of steel hardening, investigates a scheduling problem to min-
imize the idle energy consumption of machines. The energy minimization is achieved by switching a machine
to some power-saving mode when it is idle. For the steel hardening process, the mode of the machine (i.e.,
furnace) can be associated with its inner temperature. Contrary to the recent methods, which consider only
a small number of machine modes, the temperature in the furnace can be changed continuously, and so an
infinite number of the power-saving modes must be considered to achieve the highest possible savings. To
model the machine modes efficiently, we use the concept of the energy function, which was originally intro-
duced in the domain of embedded systems but has yet to take roots in the domain of production research. The
energy function is illustrated with several application examples from the literature. Afterward, it is integrated
into a mathematical model of a scheduling problem with parallel identical machines and jobs characterized
by release times, deadlines, and processing times. Numerical experiments show that the proposed model
outperforms a reference model adapted from the literature.
1 INTRODUCTION
In recent years, there has been an increasing inter-
est in energy-efficient scheduling (Gahm et al., 2016;
Gao et al., 2019). The reasons are both ecological and
economical. By implementing efficient scheduling, a
significant amount of energy can be saved (Mouzon
et al., 2007; Gahm et al., 2016) with negligible in-
vestments.
This paper addresses a scheduling problem to
minimize the total idle energy consumption of the ma-
chines. Our work is inspired by a steel hardening pro-
cess, which has high energy demands. During the
process, a material is heated to a very high temper-
ature (defined by the technological process) in one of
the identical furnaces. A segment of the production
line with several furnaces in
ˇ
Skoda Auto company is
shown in Figure 1. There, parts of the future gear
shafts are hardened. The operating temperature of the
furnaces is 960
◦
C. Typically, the furnaces are heated
a
https://orcid.org/0000-0002-7365-844X
b
https://orcid.org/0000-0003-4895-157X
c
https://orcid.org/0000-0002-8135-1296
Figure 1: A steel hardening production line in
ˇ
Skoda Auto
consisting of electrical vacuum furnaces (Du
ˇ
sek, 2016).
to the operating temperature at the beginning of the
weak, and cooled down at its end. However, some
of the furnaces might not be utilized all the time, de-
pending on the previous production stages.
If the furnace is underutilized, energy can be saved
by lowering the temperature during the idle periods.
However, the furnace needs to be heated back to the
operating temperature before the next job arrives. As
Benedikt, O., Š˚ucha, P. and Hanzálek, Z.
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model.
DOI: 10.5220/0008877400350046
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 35-46
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
35

600
800
960
Temperature [
◦
C]
0
50
100
150
200
250
0
50
100
150
160 kW
40 kW
18 kW
Time [min]
Power [kW]
cooling holding heating
Figure 2: A relationship between the power consumption
and the temperature of a single furnace during the experi-
ment.
re-heating of the furnace takes time and consumes en-
ergy, it needs to be planned carefully. Our prelim-
inary study in
ˇ
Skoda Auto company has shown that
over 5 % of the energy consumption of the harden-
ing line could be saved by switching the idle furnaces
to the power-saving modes (Du
ˇ
sek, 2016). Several
experiments were performed to investigate the poten-
tial for energy savings. During one of the experi-
ments, the furnace was heated to the operating tem-
perature, i.e., 960
◦
C; afterward, it cooled to 600
◦
C
and was re-heated back to 960
◦
C. Figure 2 shows
the relationship between the temperature and power.
Note that during the cooling phase, the input power is
zero. On the other hand, the maximal power (160 kW)
is applied for the re-heating to reach the operating
mode as soon as possible. The experiment shows
that the power needed to compensate for the losses
when holding 960
◦
C (about 40 kW) is more than two
times higher than the power needed for 600
◦
C (about
18 kW). That indicates the potential for energy sav-
ing. Of course, if the machine were turned off com-
pletely (i.e., to the ambient temperature), the power
consumption during the holding phase would be zero.
However, the complete cooling and re-heating would
require a considerably longer time (which might not
be available). Also, the energy needed for re-heating
would be higher. Therefore, depending on the idle
period length, different savings might be achieved by
cooling to different temperatures.
1.1 Contributions and Outline
This study aims to contribute to the growing area of
energy optimization research by providing an exam-
ple of the parallel machine problem, its formal de-
scription, and a formulation of a Mixed Integer Lin-
ear Programming (MILP) model. Compared to the
other problems of the idle energy optimization stud-
ied in the literature, this one is special because the
slow dynamics of the machine (furnace) and its “in-
ner state” (temperature) cannot be neglected. The
proposed MILP model takes into account possible
power-saving modes indirectly by using the energy
function, which abstracts the dynamics of the ma-
chine. The proposed model is compared with an-
other MILP model, adapted from the literature, and
its performance is further tested on a set of bench-
mark instances. Also, this paper shows that the en-
ergy function can easily replace conventional model-
ing approaches (e.g., those using on/off or on/idle/off
modes).
The rest of the paper is organized as follows. Sec-
tion 2 summarizes connections to relevant literature.
Section 3 formally describes the studied scheduling
problem. Afterward, the abstraction used for idle en-
ergy optimization, called the energy function, is in-
troduced in Section 4, together with several exam-
ples from the literature. Section 5 describes the MILP
model, which integrates the energy function. In Sec-
tion 6, the proposed model is compared to a reference
model, and its scalability is tested on a range of in-
stances. Finally, Section 7 gives a summary of the
findings.
2 RELATED WORK
In the area of production scheduling, one of the
first analyses of underutilized machines was done by
Mouzon et al. (2007), who observed that changing
the machine modes could reduce energy consumption
significantly. Furthermore, they proposed a mathe-
matical model to optimize energy and the completion
time by turning the machine on and off. However, the
model optimized a single machine only, assuming a
fixed order of the jobs.
In the domain of single machine problems, Shrouf
et al. (2014) proposed a mathematical model and
heuristics for a single machine with three modes (pro-
cessing, idle and shut down), assuming variable en-
ergy prices. Gong et al. (2016) also addressed a prob-
lem with dynamic energy pricing, modeling a sin-
gle machine with multiple processing modes by a fi-
nite state automaton. After completion of each job,
the machine could stay idle, shut down, or start pro-
cessing the next job. No power-saving modes be-
sides the shutdown mode were allowed. Furthermore,
it was assumed that transitions between the individ-
ual modes of the machine are immediate. This as-
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
36

sumption cannot be used here, because heating and
cooling take time. A single machine problem was
also investigated by Che et al. (2017), who optimized
weighted energy consumption and makespan and de-
ployed cluster analysis to approximate Pareto fronts
of large-size problems. Their problem statement is
similar to ours, but they scheduled on and off modes
only, which might be too restrictive when the com-
plete power-down takes a long time.
Compared to the single machine problem, paral-
lel machine scheduling studied here is much harder,
because the assignment of the jobs to machines needs
to be found together with their relative order and start
times. Fang and Lin (2013) described a MILP model,
dispatching heuristics, and a particle swarm optimiza-
tion algorithm for the weighted tardiness/cost prob-
lem. They assumed that the processing time of a job
could be shortened by increasing the speed of the ma-
chine, which is not the case for the problem studied
here because the hardening process needs to follow a
given technological specification. Furthermore, their
MILP model was relatively slow even for five jobs
scheduled on three machines. Liang et al. (2015) for-
mulated a non-linear model of an on/off problem with
unrelated parallel machines and proposed an ant opti-
mization heuristic. Masmoudi et al. (2017) developed
a mathematical model and heuristic for a flow shop
problem with time-of-use energy pricing, and Meng
et al. (2019) proposed MILP models for a flexible job
shop problem, where on and off modes of the ma-
chines were considered. Benedikt et al. (2018) for-
mulated a parallel machine scheduling problem with
multiple processing modes with different processing
speeds and power consumption. A decomposition-
based approach based on the column generation tech-
nique was proposed to solve the problem. However,
the resulting mathematical models are still very com-
plex and have limited scalability. M
´
odos. et al.
(2019) studied a scheduling problem with dedicated
machines, inspired by glass tempering and steel hard-
ening processes. Instead of energy minimization, the
energy consumption limit (imposed for each metering
interval) was considered. However, the authors did
not model the power-saving modes of the machine,
which might have a positive impact on energy con-
sumption in the metering intervals when some of the
machines are idling.
Reviews of energy-efficient scheduling were pub-
lished by Gahm et al. (2016) and Gao et al. (2019),
who summarized the latest trends in the area. The re-
views show that interest in energy-efficient schedul-
ing is steadily increasing year by year. Also, the
reviews show that a mixed-integer (linear) program-
ming is one of the standard modeling techniques used
in the area.
We conclude that although the idle energy mini-
mization is widely studied, only two or several modes
of the machines are commonly modeled, which might
be too restrictive. Also, the unifying concept of the
idle energy consumption modeling (i.e., the energy
function) is still not widely known.
3 PROBLEM STATEMENT
3.1 Input Parameters and Assumptions
We consider a finite set of jobs J = {J
1
, J
2
, . . ., J
n
}
and a finite set of parallel identical machines M =
{M
1
, M
2
, . . ., M
m
}. Each job J
i
is characterized by
three non-negative integers: processing time p
i
, re-
lease time r
i
, and deadline
˜
d
i
. Release time and dead-
line form an execution time window within which the
job needs to be processed. Each job can be processed
on any machine, but each machine can process only
a single job at a time. When the processing starts, it
cannot be preempted.
While a job is processed, the machine needs to be
operating in a processing mode (heated to predefined
operational temperature T
oper
) and cannot change it
until the processing of the job is finished. The pro-
cessing of job J
i
consumes energy E
(proc)
i
. When a
machine does not process any job, it enters a so-called
idle period. During the idle period, the temperature
can be changed to achieve energy savings, but when
the next job arrives, the machine needs to be heated
back to T
oper
. The relationship between energy con-
sumption and the length of the idle period ∆ is given
by energy function E : R
≥0
→ R
≥0
. For fixed ∆, value
E(∆) represents the best attainable energy consump-
tion across all available machine modes. The energy
function is further discussed in Section 4.
It is assumed that each machine starts and ends
in “off-mode”, which has zero power consumption.
Some machines may remain in the off-mode all the
time, but at least one machine needs to be turned on
to process the jobs. The energy needed for the switch-
ing from off-mode to the processing mode and back
is given by E
(start)
∈ R
>0
. It is assumed that there
is enough time to turn the machines on before the
first job is available and to turn them off after the last
job is processed. In the following text, the length
of the scheduling horizon is denoted by H, where
H = max{
˜
d
i
| J
i
∈ J }.
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model
37

3.2 Solution Representation
Solution S can be represented by a pair of vec-
tors, S = (a
a
a, s
s
s), where vector s
s
s = (s
1
, . . ., s
n
) ∈ Z
n
≥0
represents start times of the jobs, and vector
a
a
a = (a
1
, . . ., a
n
) ∈ M
n
captures assignment of the
jobs to machines. The solution is feasible if all jobs
are processed within their execution windows without
preemption or overlapping.
3.3 Optimization Objective
The assignment of the jobs, together with their start
times, define the idle periods in the schedule. De-
pending on their lengths, energy consumption may
vary.
Before defining the objective, let us denote the in-
dex of the job scheduled immediately before job J
i
in
solution S on machine a
i
by pred
S
(i). If such a job
does not exist, i.e., the job J
i
is the first on machine
a
i
, we define pred
S
(i) := 0. Now, the energy con-
sumption corresponding to solution S can be written
as follows:
n
∑
i=1
E
(proc)
i
+
n
∑
i=1
pred
S
(i)6=0
E(s
i
− s
pred
S
(i)
− p
pred
S
(i)
) +
n
∑
i=1
pred
S
(i)=0
E
(start)
,
(1)
where the first sum represents the total energy needed
to process the jobs, the second sum corresponds to
the energy consumed during the idle periods (energy
function E is further described in Section 4), and the
third sum express the energy needed for turning the
machines (to which at least one job is assigned) on
and off. The optimal schedule minimizes the total en-
ergy consumption (1).
Note that constant
∑
n
i=1
E
(proc)
i
can be omitted for
the optimization as it does not affect the structure of
the optimal schedule.
3.4 Complexity
Using the standard α|β|γ notation, we can character-
ize the studied problem as P|r
j
,
˜
d
j
|E
idle
, meaning idle
energy minimization for parallel identical machines
and jobs characterized by release times and dead-
lines. The problem is N P -hard because its subprob-
lem 1|r
j
,
˜
d
j
|− is already N P -complete in the strong
sense (Garey and Johnson, 1977).
4 ENERGY FUNCTION
The energy function is a concept used when idle en-
ergy minimization is taken into account. The spe-
cific properties of the resource are abstracted, and
only the information about the energy consumption
is explicitly represented. This concept often simpli-
fies the analysis of the problem properties, as well as
the models and algorithms. Here, we establish the
basic notions in Section 4.1 and show several exam-
ples from the literature in Section 4.2. Afterward, we
discuss the energy function obtained for vacuum fur-
naces studied in this paper in Section 4.3.
4.1 Basic Notions
Denoting V the set of all machine modes, a basic ma-
chine model can be described as follows. When the
machine processes a job, it needs to be operating in
the processing mode “proc”. When no job is pro-
cessed, the machine can change the mode. Switch-
ing to (non-processing) mode v and back takes time
T
v
, and consumes energy E
v
. The power consump-
tion of the machine in mode v is denoted by P
v
, and is
assumed to be constant. Depending on the length of
the idle period between two neighboring jobs, which
is denoted by ∆, a machine can either turn to some
non-processing mode (and back) or remain in the pro-
cessing mode. Clearly, if ∆ is shorter than T
v
, switch-
ing to mode v is not feasible. Also, switching to a
power-saving mode should be only performed when
it would not increase the overall power consumption
(Devadas and Aydin, 2012). These observations lead
us to the following formulation of the energy con-
sumption function E : R
≥0
→ R
≥0
(Gerards and Ku-
per, 2013):
E(∆) = min
v∈V :∆≥T
v
{E
v
+ P
v
· (∆ −T
v
)}. (2)
Formally, we define T
proc
= E
proc
= 0, i.e., for
V = {proc}, E(∆) = P
proc
· ∆.
The value E(∆) represents the best attainable en-
ergy consumption for given idle period length ∆. Note
that the optimal mode to which the machine should be
switched is given by the argument of the minimum in
(2). In the following section, we discuss several ap-
plications of this model.
4.2 Examples from the Literature
Concept of the idle energy minimization is relatively
old. Initially, the possibilities of the power savings
were investigated in the field of embedded systems
(Benini et al., 2000; Augustine et al., 2008; Gerards
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
38
0 20 40
60
0
1
2
·10
4
8
processing
mode 1
mode 2
mode 3
mode 4
∆ [ms]
E [mJ]
processing
mode 1
mode 2
mode 3
mode 4
Figure 3: The energy function of a sensor node from em-
bedded systems domain (Sinha and Chandrakasan, 2001).
and Kuper, 2013), where energy consumption plays
a critical role for the lifetime of the battery-powered
systems. Nowadays, it is common that hardware com-
ponents have one or several power-saving modes de-
fined by the manufacturer (Gerards and Kuper, 2013).
Of course, the time and energy needed to perform the
transitions between the modes are usually not negligi-
ble. Therefore, the selection of the “optimal” power-
saving mode of the component depends on the idle
period length.
An example of a hardware device with multiple
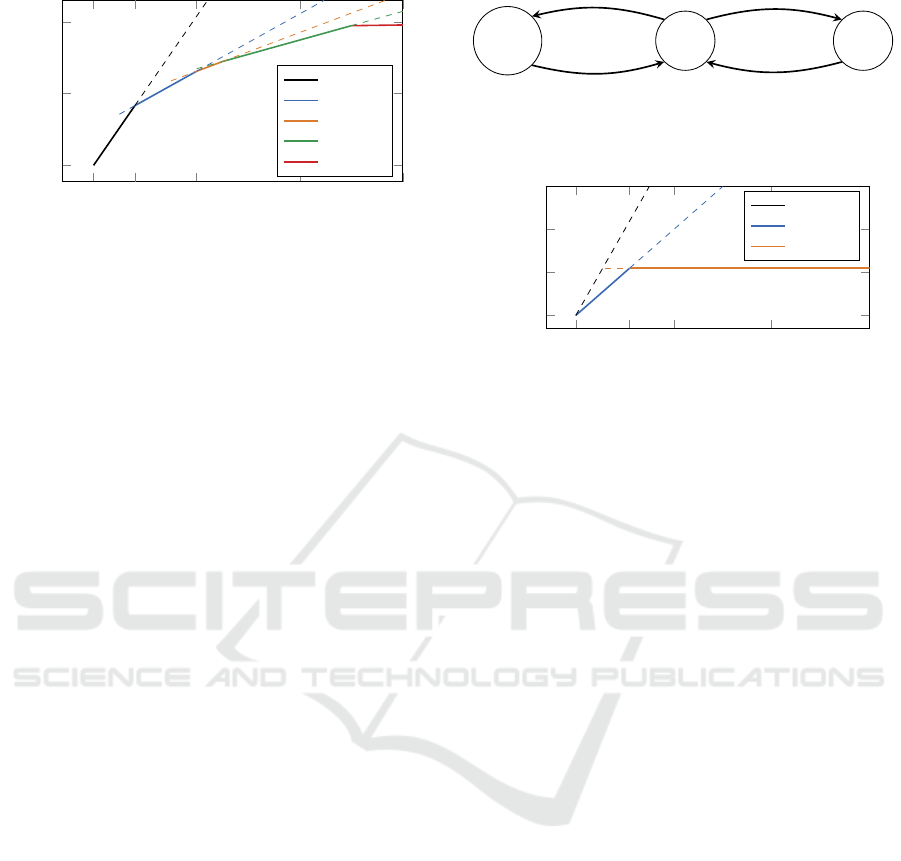
modes is a sensor node (Sinha and Chandrakasan,
2001), which has four power-saving modes, with T
v
equal to 5, 15, 20, and 50 milliseconds, respectively.
The piecewise linear function drawn by a solid line in
Figure 3 is the energy function of the device. It con-
sists of 5 segments, corresponding to different modes
of the device. Note that even though mode 1 is acces-
sible already for ∆ = 5, it is not profitable to perform
the switching until ∆ = 8, which is called a break-even
time in the literature (Devadas and Aydin, 2012).
In the production domain, research of the idle en-
ergy minimization is still relatively new. The interest
in the topic increased after Mouzon’s study, which an-
alyzed underutilized machines (Mouzon et al., 2007).
Since that time, researchers have started to take the
power-saving modes of the machines into consider-
ation. However, only a small number of modes is
usually considered (Shrouf et al., 2014; Che et al.,
2017; Aghelinejad et al., 2019). Typically, the ma-
chine modes and transitions are modeled by a transi-
tion graph. A representative example of such a graph
is shown in Figure 4 (Shrouf et al., 2014). The nodes
are labeled by power consumption, while the edges
are labeled by energy/time needed for the transition.
Parameters needed for the energy function can be eas-
ily obtained from the graph. For example, T
off
= 3 h,
E
off
= 11kW h, P
off
= 0kW, etc. The corresponding
energy function is shown in Figure 5.
standby
proc
off
2 kW 4 kW
0 kW
0 kW h / 0 h
0 kW h / 0 h
10 kW h / 2 h
1 kW h / 1 h
Figure 4: Example of a transition graph depicting machine
modes and transitions between them (Shrouf et al., 2014).
0 10 20 30
0
10
20
30
5.5
processing
standby
off
∆ [h]
E [kW h]
processing
standby
off
Figure 5: Energy function corresponding to the transition
graph depicted in Figure 4.
4.3 Energy Function and Industrial
Furnaces
When considering the industrial furnaces, the situ-
ation is slightly more complicated because of their
slow dynamics. Depending on the input power, the
furnace is either cooling (temperature inside is de-
creasing), holding (temperature inside is stable), or
heating (temperature inside is increasing), as shown
in Figure 2. We could associate the mode v of the
furnace with the temperature that should be held in-
side of the furnace. The power consumption P
v
is then
the power needed to compensate for the steady-state
losses of the furnace. The switching time T
v
is the
time needed for cooling plus the time needed for re-
heating, and the switching energy consumption E
v
is
equal to the energy needed for cooling (which equals
zero) and the energy needed for re-heating.
Now, if we wanted to model such a system by a
transition graph, we would face a problem, as only a
finite number of machine modes can be modeled like
that. On the other hand, the temperature in the fur-
nace can be changed continuously, and so an infinitely
large set V would be needed to model all possible
power-saving modes.
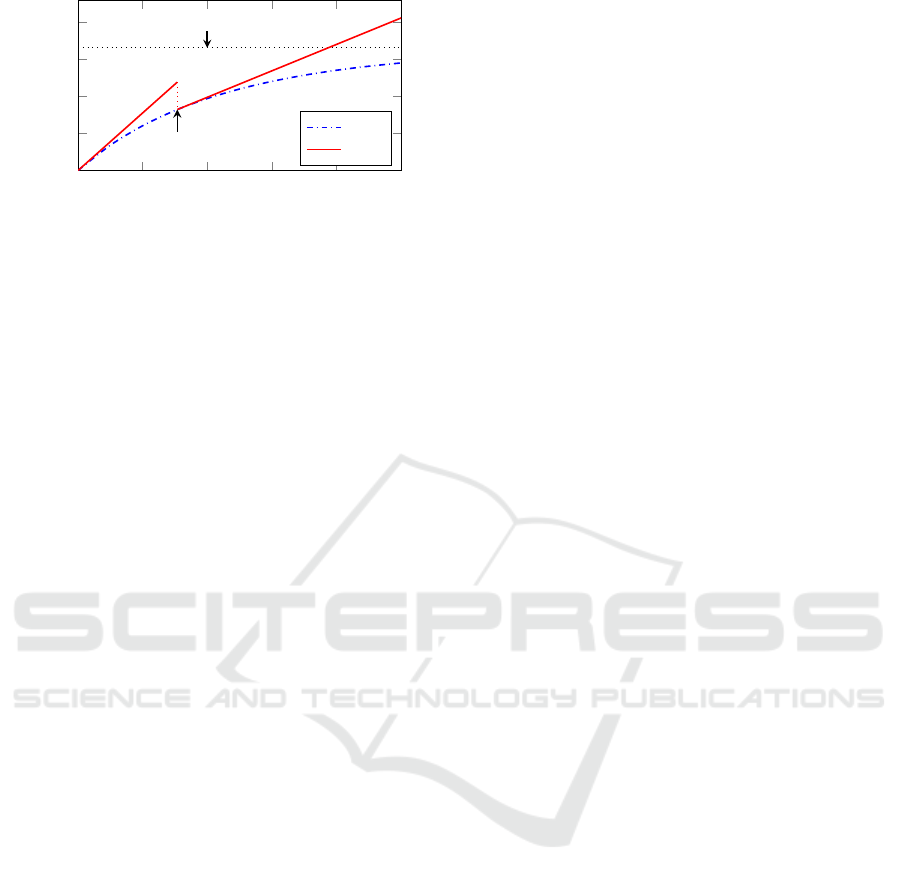
Figure 6 shows two possible energy functions of
the furnace corresponding to two different control
strategies. Function E
600
represents a standard ap-
proach using a transition graph with a single power-
saving mode associated with the temperature 600
◦
C.
The corresponding control rule states: cool to 600
◦
C,
hold 600
◦
C as long as possible and re-heat to the
operating temperature as fast as possible just be-
fore the end of the idle period. The slope of the
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model
39
0 100 200 300 400
500
0
40
80
120
160
asymptote of E
cont
T
600
processing
holding 600
◦
C
∆ [min]
E [kW h]
E
cont
E
600
Figure 6: Energy function of an industrial furnace E
cont
in-
tegrating all power-saving modes (Benedikt et al., 2019),
and function E
600
corresponding to a single power-saving
mode.
first segment of E
600
corresponds to the power con-
sumption of the processing mode, while the slope of
the second segment corresponds to the power com-
pensating for the losses when holding 600
◦
C. Energy
E
600
(T
600
) is the energy needed to re-heat the furnace
from 600
◦
C back to the 960
◦
C (remember that en-
ergy needed for cooling is zero). Transition to the
power-saving mode is not possible during time inter-
val [0, T
600
), because there is not enough time to cool
the furnace to 600
◦
C and re-heat it back.
On the other hand, function E
cont
is a result
of a detailed analysis of the industrial furnace, see
Benedikt et al. (2019). The control rule states that
the furnace should be cooling as long as possible, and
should be re-heated as fast as possible to reach the
operating mode again at the end of the idle period.
With the increasing length of the idle period, the tem-
perature to which the furnace cools decreases until it
reaches the ambient temperature. Then, the energy
needed to cool to the ambient temperature and to re-
heat back corresponds to the asymptote shown by the
dashed line.
Note that when only a subset of all modes is con-
sidered, the energy function becomes discontinuous,
like E
600
. The reason for the discontinuity is that the
cooling of the furnace is slow, and so the integral of
the processing power over interval [0, T
600
] becomes
greater than the switching energy consumption E
600
.
Contrary to that, function E
cont
, which implicitly rep-
resents all possible temperatures, remains continuous
and concave (similarly to the energy functions shown
in Figures 3 and 5).
5 MATHEMATICAL MODEL
In this section, we integrate the energy function into
a MILP model proposed for the problem defined in
Section 3.
As shown by Gahm et al. (2016), formulating
problems by MILP models and solving them by
standard solvers has been one of the widely used
approaches to the optimal energy-aware schedul-
ing. There exist several alternative approaches to the
scheduling problem modeling in MILP. Many authors
use time-indexed models (Shrouf et al., 2014; Mitra
et al., 2012; Masmoudi et al., 2017) – scheduling hori-
zon is divided into periods and decisions about the
mode of the machine or assignment of jobs have to
be made for each period separately. In many cases,
the time-indexed models are the only reasonable al-
ternative, e.g., when the properties of the system vary
through time. However, the size of a time-indexed
model depends on the length of the scheduling hori-
zon, which is prohibitive.
Other formulation approaches use event-based
modeling (Kon
´
e et al., 2011), permutation (position-
based) models (Che et al., 2017), or relative order
models (Liang et al., 2015).
The model we propose in this work is a special
variant of the relative-order model, modeling the di-
rect predecessor and successor of each job. A similar
idea has already been used in the scheduling domain
successfully (Liu et al., 2008). However, we inte-
grate the concept of the energy consumption function
into the model formulation to describe the transition
costs efficiently. The model is compared to a position-
based model in Section 6.
5.1 Model Description
At first, we define two dummy jobs; the first one,
J
s
(dummy-start), is fixed to start and end at time
0, while the second one, J
e
(dummy-end), must start
and end at time H. Both have zero processing length.
These dummy jobs model the predecessor (successor)
of the first (last) job assigned to each machine.
5.1.1 Variables
We use five types of variables to model the problem.
Binary variables are:
a
i,k
indicates if job J
i
is assigned to machine M
k
y
i, j,k
decides whether job J
i
immediately precedes
job J
j
on machine M
k
x
k
indicates whether at least one job is assigned
to machine M
k
Continuous variables follow:
s
i
corresponds to start time of job J
i
z
i, j
equals to the length of the idle period between
jobs J
i
and J
j
if J
i
immediately precedes J
j
,
otherwise 0
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
40

Variables y
i, j,k
are defined for jobs including the
dummies. All the other variables are defined for non-
dummy jobs only. Note that variables z
i, j
model the
lengths of idle periods ∆.
5.1.2 Objective
As discussed in Section 3.3, the objective is to min-
imize the total idle energy consumption plus the en-
ergy needed to power the machines up and turn them
down (if there is at least one job assigned to the ma-
chine). Using the defined variables, we can write the
whole objective as
∑
i∈J
∑
j∈J
i6= j
E(z
i, j
) + E
(start)
·
∑
k∈M
x
k
. (3)
The non-linear energy function E is approximated
by a piecewise linear function. The approximation
can be made simply and with high precision even
with a small number of segments, thanks to the simple
shape of the energy function.
Note that functions corresponding to finite transi-
tions graph, such as the ones shown in Figure 3 and
Figure 5, are already piecewise linear by definition
(2).
The piecewise linear objective function can be fur-
ther linearized by introducing additional binary and
continuous variables. However, modern solvers, such
as Gurobi or CPLEX, can optimize piecewise linear
objectives natively. The linearization is handled inter-
nally, and solvers may even benefit by using special-
ized data structures and algorithms.
5.1.3 Constraints
Equations (4) force each job to be assigned to exactly
one machine. Constraints (5) and (6) define that if job
J
i
is scheduled to machine M
k
, it has exactly one im-
mediate predecessor and successor on that machine,
and otherwise if it is not assigned to machine M
k
,
it cannot precede and follow any other job on that
machine. Constraints (7) and (8) force dummy-start
(dummy-end) to have exactly one successor (prede-
cessor) on each machine. Execution time windows
of the jobs are established by (9), whereas constraints
(10) forbid overlapping of the neighboring jobs. In-
equalities (11), (12) and (13) link variable z
i, j
to the
length of the respective idle period. If job J
i
pre-
cedes job J
j
on some machine, z
i, j
is exactly equal
to s
j
− (s
i
+ p
i
), i.e., to the length of the idle period
between those two consecutive jobs; otherwise, it is
set to zero. Finally (14) forces x
k
to 1, if there is at
least one job assigned to this machine. Symbol M
represents some large constant (e.g., M = H).
∑
M
k
∈M
a
i,k
= 1, J
i
∈ J (4)
∑
J
j
∈J ∪{J
e
}
j6=i
y
i, j,k
= a
i,k
, J
i
∈ J , M
k
∈ M (5)
∑
J
j
∈J ∪{J
s
}
j6=i
y
j,i,k
= a
i,k
, J
i
∈ J , M
k
∈ M (6)
∑
J
i
∈J ∪{J
e
}
y
j,i,k
= 1, M
k
∈ M , J
j
= J
s
(7)
∑
J
i
∈J ∪{J
s
}
y
i, j,k
= 1, M
k
∈ M , J
j
= J
e
(8)
r
i
≤ s
i
≤
˜
d
i
− p
i
, J
i
∈ J (9)
s
i
+ p
i
+ z
i, j
≤ s
j
+ M ·(1 − y
i, j,k
),
J
i
∈ J , J
j
∈ J , M
k
∈ M
(10)
s
j
− (s
i
+ p
i
) ≤ z
i, j
+ M ·(1 −
∑
M
k
∈M
y
i, j,k
),
J
i
∈ J , J
j
∈ J , i 6= j
(11)
s
j
− (s
i
+ p
i
) ≥ z
i, j
− M ·(1 −
∑
M
k
∈M
y
i, j,k
),
J
i
∈ J , J
j
∈ J , i 6= j
(12)
z
i, j
≤ M ·
∑
M
k
∈M
y
i, j,k
, J
i
∈ J , J
j
∈ J , i 6= j (13)
x
k
≥ (1 − y
i, j,k
), M
k
∈ M , J
i
= J
s
, J
j
= J
e
(14)
Besides the constraints mentioned above, which
define the behavior of the model, additional con-
straints can be added to reduce the search space by
eliminating symmetries. Constraints (15) state that
jobs are preferably assigned to machines with lower
indices. Constraints (16) pre-assign the first job to the
first machine, the second job to the first or the second
machine, etc.
x
k
≥ x
k+1
, M
k
∈ {1, . . . , m − 1} (15)
i
∑
k=1
a
i,k
= 1, i ∈ {1, . .. , min{m, n}} (16)
To further reduce the solution space, we use ad-
ditional constraints that link the lengths of the gaps
with the start times of the jobs – stating that all the
gaps and jobs should ‘fill’ the whole scheduling hori-
zon. For that, we add new variables start
k
and end
k
,
which denote the start time of the first job processed
on machine M
k
, and the ending time of the last job
processed on machine M
k
, respectively. It must hold
that if job J
i
follows immediately after J
s
on ma-
chine M
k
, then start
m
= s
i
. Similarly, if job J
i
im-
mediately precedes J
e
on machine M
k
, then end
k
=
H − (s
i
+ p
i
), where H is the length of the schedul-
ing horizon. These logical implications in the form
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model
41

if x = 1 then y = z with binary variable x and continu-
ous variables y and z can be linearized by introducing
two constraints:
y − z ≤ M(1 − x), and z − y ≤ M(1 − x).
Now, constraint (17) can be added:
n
∑
i=1
p
i
+
n
∑
i=1
n
∑
j=1
i6= j
z
i, j
+
m
∑
k=1
(start
k
+ end
k
) = H
m
∑
k=1
x
k
.
(17)
6 EXPERIMENTS
To test the performance of the proposed model, we
conduct two types of experiments. The first experi-
ment compares our model to the position-based model
adopted from the relevant paper (Che et al., 2017),
and the second experiment examines the scalability
of our model on larger problem instances.
For each experiment, a wide range of instances is
generated for different combinations of n and m. The
optimality gap is used to measure the performance of
the model(s). In the following text, U{x, y} stands
for an integer uniform distribution on interval [x, y],
Exp(x) denotes the exponential distribution with scale
parameter x, and E(p
i
) represents the expected pro-
cessing time of job i.
All experiments were performed on a Dell PC
with an Intel Core i7-4610M CPU operating at 3 GHz,
16 GB RAM. Gurobi Optimizer (version 8.1) was
used to solve the MILP models.
6.1 Benchmark Data
Jobs’ parameters are generated according to the fol-
lowing scheme. At first, vector a
a
a = (a
1
, . . ., a
n
) is
generated, a
i
∼ U{1, m}, describing the random as-
signment of the jobs to machines. Note that vector
a
a
a is used only for data generation, simulating the pro-
duction process. It might be different from the assign-
ment found by the optimization solver.
Processing times, release times, and deadlines are
generated according to (18), (19) and (20), respec-
tively.
p
i
∼ U{p
min
, p
max
} (18)
r
i
∼
i−1
∑
k=1
Ja
k
= a
i
K · E(p
i
) + Exp(α· E(p
i
)) (19)
˜
d
i
∼ r
i
+ p
i
+ β ·E(p
i
) + Exp(γ· E(p
i
)) (20)
Processing times, release times, and deadlines are
assumed to be integers, so only the upper integer part
of the generated data is considered. Symbols p
min
,
p
max
, α, β and γ represent parameters, which allow us
to generate instances with different properties. Indi-
cator Ja
k
= a
i
K is one if a
k
= a
i
, and zero otherwise.
Experiment 1: Comparison with a Position-based
Model
In this experiment, we compare our model to the
position-based model, which was originally devel-
oped by Che et al. (2017) for a single machine prob-
lem. As the problem studied in this paper differs from
the problem studied by Che et al., it was necessary to
modify their model slightly. The modified model is
described in Appendix. For both models, additional
constraints (15–17), and (29–31) were used.
Because the reference position-based model opti-
mizes the energy consumption for two modes only,
energy function E
600
with a single switching depicted
in Figure 6 was used for the experiment. There
were 50 testing instances randomly generated for each
combination of n ∈ {10, 15, 20}, m ∈ {1, 2, 4}, α ∈
{0.8, 1.2} and γ ∈ {1, 1.5}; (1800 instances in total).
Parameter β was set to 1. The minimal and maximal
processing times p
min
, and p
max
, were set to 1 and
300, respectively. The time limit was set to 300 s per
instance.
The overall results of the experiment are shown in
Table 1. Each row aggregates 200 instances; 50 gen-
erated for each combination of α and γ. A number
of infeasible instances is given by #if. A number of
timeouts is listed in the table in the columns #to. The
average runtimes are measured and listed for feasi-
ble and infeasible instances separately, where t
if
and
t
f
represent the average time over infeasible and fea-
sible instances, respectively. Average times that are
typed in the bold font mark the better of the two tested
solvers. The average optimality gap is listed as well
(computed over all instances aggregated in the given
row). Solving times aggregated over all feasible in-
stances are also depicted in Figure 7 in the form of
box plots.
The single machines instances were solved by
both models without any problems. The performance
of the position-based model was slightly better. How-
ever, the absolute times of both models were low. In-
stances with parallel machines are harder to solve be-
cause the assignment needs to be found together with
the order of the jobs. Results show that our model
outperformed the reference model when the number
of machines was higher than 1. The biggest differ-
ence can be seen for m = 2, n = 20, where the refer-
ence model ran out of time three times more often,
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
42
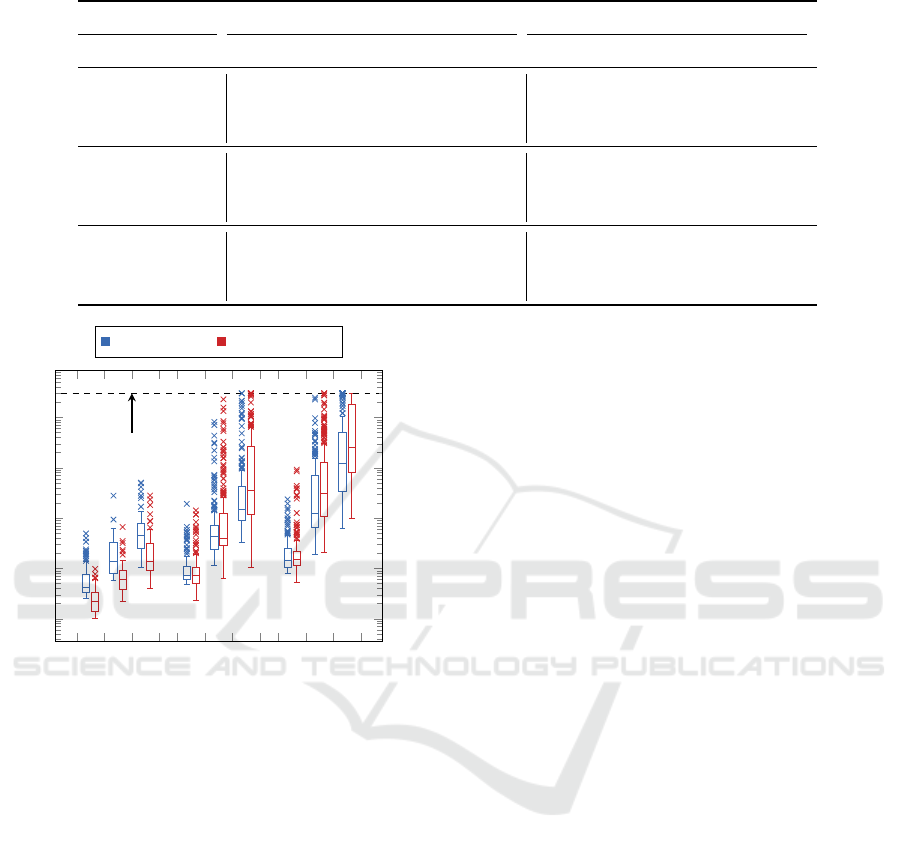
Table 1: Comparison between the position-based model and the relative-order model.
Instances Position-based (reference) Relative-order (this work)
n m #if #to t
if
[s] t
f
[s] gap [%] #to t
if
[s] t
f
[s] gap [%]
1 87 0 0.01 0.03 0.00 0 0.03 0.08 0.00
10 2 6 0 0.39 0.12 0.00 0 0.41 0.12 0.00
4 0 0 - 0.37 0.00 0 - 0.24 0.00
1 126 0 0.02 0.08 0.00 0 0.07 0.24 0.00
15 2 12 1 56.09 6.29 0.00 0 1.99 2.38 0.00
4 0 4 - 23.80 0.45 0 - 8.64 0.00
1 148 0 0.04 0.35 0.00 0 0.19 0.88 0.00
20 2 23 29 190.60 43.09 1.65 9 95.92 16.79 0.23
4 0 41 - 96.12 6.73 23 - 61.66 3.48
10-1 15-1 20-1 10-2 15-2 20-2 10-4 15-4 20-4
10
−2
10
−1
10
0
10
1
10
2
time limit
Parameters n-m
Time [s]
Relative-order Position-based
Figure 7: Comparison between the relative-order model
(left) and the position-based model (right) of the solving
times on feasible instances for different pairs of n and m.
and performed more than 2.5 times slower on the fea-
sible instances on average. The difference is not that
large for m = 4, n = 20, because both models started
to reach the maximum solving time (see Figure 7).
Considering the optimality gap, the average over-
all instances for which at least one of the models did
not find an optimal solution was 23.02 % for the ref-
erence model and 9.84 % for our model.
The total run time was 37 987 s for the reference
model and 19 894 s for our model, so our model was
nearly two times faster on average. Furthermore, it is
important to note that our model can optimize any en-
ergy function, which can be approximated by a piece-
wise linear function, whereas the reference model was
developed to optimize the on/off modes only.
Experiment 2: Scalability
In the second experiment, the proposed model is
tested on larger instances. For the experiment, a
piecewise linear approximation of energy function
E
cont
shown in Figure 5 was used. The approxi-
mation was made by 17 linear segments. Ten in-
stances were generated for each combination of n ∈
{20, 25, 30, 35}, m ∈ {2, 4,6}, α ∈ {1, 1.5}, and γ ∈
{1, 2}; 480 instances in total. Parameter β was set to
1. Parameters p
min
and p
max
were again set to 1 and
300, respectively. The maximal time limit was set to
10 min per instance.
The results are listed in Table 2. Each row aggre-
gates 40 instances generated for each combination of
α and γ. Column #if shows the number of infeasible
instances, #to
if
(#to
f
) represents the number of time-
outs on infeasible (feasible) instances, t
if
(t
f
) is the
average time on the respective instances, and ‘gap’ is
the average optimality gap over the feasible instances,
for which some solution was found.
Table 2 shows how the complexity increases with
the increasing number of jobs and machines. The
performance of the model, which includes additional
constraints (15), (16), and (17), is compared to the
same model without these constraints.
The results show that the additional constraints
significantly improve the behavior of the model.
The overall average optimality gap decreases from
40.73 % to 14.20 % when the constraints are used.
Also, the number of optimally solved instances in-
creases from 119 to 233, and the number of timeouts
decreases from 343 to 226. The ability to find a fea-
sible solution is comparable for both models – model
without symmetry breaking constraints finds a solu-
tion to 414 instances, while the model with symmetry
breaking constraints finds a solution to 433 instances
(out of 450 feasible instances).
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model
43
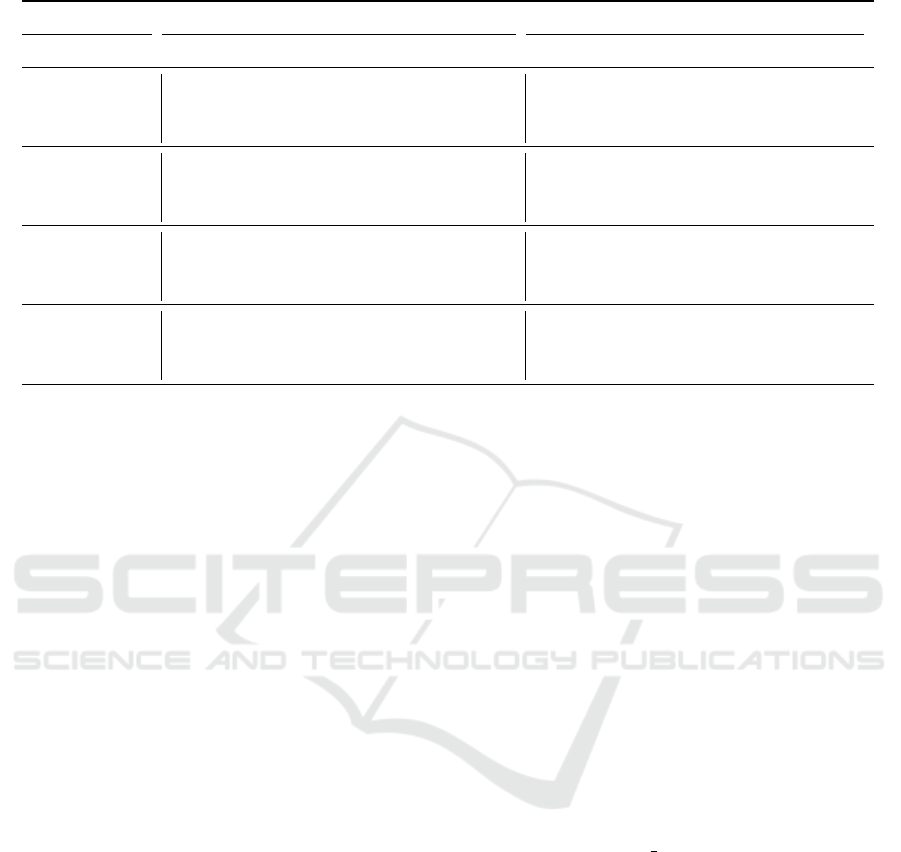
Table 2: Performance of the relative-order model on larger instances.
Instances Relative-order (without additional constr.) Relative-order (with additional constr.)
n m #if #to
if
#to
f
t
if
[s] t
f
[s] gap [%] #to
if
#to
f
t
if
[s] t
f
[s] gap [%]
2 10 1 3 94 103 4.39 0 2 56 56 0.41
20 4 0 0 26 - 452 36.07 0 11 - 220 7.98
6 0 0 30 - 501 47.17 0 13 - 235 11.26
2 4 2 10 305 229 7.22 1 5 157 141 2.27
25 4 0 0 33 - 531 50.50 0 15 - 270 12.08
6 0 0 39 - 593 62.24 0 25 - 432 19.18
2 8 7 12 526 334 16.10 7 9 527 220 5.15
30 4 0 0 38 - 574 55.89 0 27 - 464 23.44
6 0 0 40 - 600 63.95 0 32 - 518 25.99
2 8 6 17 465 367 16.78 4 13 363 337 5.77
35 4 0 0 39 - 592 54.65 0 24 - 481 18.40
6 0 0 40 - 600 65.95 0 38 - 581 32.38
When the instances are large, it may be hard to
find a feasible solution or detect the infeasibility.
However, this could be solved by a simple decompo-
sition, using, for example, some heuristics or a Con-
straint programming model to check feasibility and
possibly provide a feasible assignment as an initial
solution to the MILP model.
7 CONCLUSIONS
This study addresses the modeling of an idle energy
minimization scheduling problems. The technique of
implicit modeling of the machine modes called idle
energy function, which abstracts dynamics of the ma-
chine and provides a link between the idle period
length and the optimal idle energy consumption, is
adopted from the domain of embedded systems. It is
shown that this method is applicable to a wide range
of idle energy minimization problems. Furthermore,
discussed examples illustrate that the properties of the
problems are similar across different domains, and the
shape of the energy function is the same for many rel-
evant applications.
An efficient MILP model that uses the idle energy
function is proposed to solve the scheduling problem
optimally. The proposed model is compared to the
position-based model adapted from the literature. The
experiment shows that the overall performance of our
model is significantly better when the number of ma-
chines was higher than one, even though the refer-
ence model is less general. Besides the comparison,
another experiment is conducted to show the perfor-
mance of the proposed model and the effect of the
symmetry breaking constraints on larger instances of
the problem. The importance of the additional con-
straints is apparent, as the overall optimality gap de-
creases nearly three times when the constraints are
used.
In our future research, we would like to inte-
grate the idle energy function into heuristics to solve
industrial-size instances of the problem. Also, we
want to investigate multi-objective optimization, be-
cause the trade-off between energy consumption and
productivity-related objectives (such as makespan or
the total tardiness) is known and widely studied.
ACKNOWLEDGEMENTS
This work was funded by the Ministry of Ed-
ucation, Youth and Sport of the Czech Re-
public within the project Cluster 4.0 number
CZ.02.1.01/0.0/0.0/16 026/0008432. This work
was also supported by the Grant Agency of the
Czech Technical University in Prague, grant No.
SGS19/175/OHK3/3T/13.
REFERENCES
Aghelinejad, M., Ouazene, Y., and Yalaoui, A. (2019).
Complexity analysis of energy-efficient single ma-
chine scheduling problems. Operations Research Per-
spectives, 6:100105.
Augustine, J., Irani, S., and Swamy, C. (2008). Op-
timal power-down strategies. SIAM J. Comput.,
37(5):1499–1516.
Benedikt, O., Alikoc¸, B.,
ˇ
S
˚
ucha, P.,
ˇ
Celikovsk
´
y, S.,
and Hanz
´
alek, Z. (2019). A scheduling and con-
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
44

trol approach for an industrial furnace to mini-
mize idle energy consumption. arXiv e-prints, page
arXiv:1910.07501.
Benedikt, O.,
ˇ
S
˚
ucha, P., M
´
odos, I., Vlk, M., and Hanz
´
alek,
Z. (2018). Energy-aware production scheduling with
power-saving modes. In van Hoeve, W.-J., editor, Inte-
gration of Constraint Programming, Artificial Intelli-
gence, and Operations Research, pages 72–81, Cham.
Springer International Publishing.
Benini, L., Bogliolo, A., and Micheli, G. D. (2000). A
survey of design techniques for system-level dynamic
power management. IEEE Transactions on Very Large
Scale Integration (VLSI) Systems, 8(3):299–316.
Che, A., Wu, X., Peng, J., and Yan, P. (2017). Energy-
efficient bi-objective single-machine scheduling with
power-down mechanism. Computers & Operations
Research, 85:172 – 183.
Devadas, V. and Aydin, H. (2012). On the interplay of
voltage/frequency scaling and device power manage-
ment for frame-based real-time embedded applica-
tions. IEEE Trans. Comput., 61(1):31–44.
Du
ˇ
sek, J. (2016). N
´
avrh
´
upravy
ˇ
r
´
ızen
´
ı v
´
yrobn
´
ı linky s ohle-
dem na sn
´
ı
ˇ
zen
´
ı jej
´
ı spot
ˇ
reby. Master’s thesis, Czech
Technical University in Prague, the Czech republic.
Fang, K.-T. and Lin, B. M. (2013). Parallel-machine
scheduling to minimize tardiness penalty and power
cost. Computers & Industrial Engineering, 64(1):224
– 234.
Gahm, C., Denz, F., Dirr, M., and Tuma, A. (2016). Energy-
efficient scheduling in manufacturing companies: A
review and research framework. European Journal of
Operational Research, 248(3):744 – 757.
Gao, K., Huang, Y., Sadollah, A., and Wang, L. (2019).
A review of energy-efficient scheduling in intelligent
production systems. Complex & Intelligent Systems.
Garey, M. and Johnson, D. (1977). Two-processor schedul-
ing with start-times and deadlines. SIAM Journal on
Computing, 6(3):416–426.
Gerards, M. E. T. and Kuper, J. (2013). Optimal DPM and
DVFS for frame-based real-time systems. ACM Trans.
Archit. Code Optim., 9(4):41:1–41:23.
Gong, X., Pessemier, T. D., Joseph, W., and Martens, L.
(2016). A generic method for energy-efficient and
energy-cost-effective production at the unit process
level. Journal of Cleaner Production, 113:508 – 522.
Kon
´
e, O., Artigues, C., Lopez, P., and Mongeau, M. (2011).
Event-based MILP models for resource-constrained
project scheduling problems. Computers & Opera-
tions Research, 38(1):3 – 13. Project Management and
Scheduling.
Liang, P., dong Yang, H., sheng Liu, G., and hua Guo,
J. (2015). An ant optimization model for unrelated
parallel machine scheduling with energy consumption
and total tardiness. Mathematical Problems in Engi-
neering.
Liu, S., Pinto, J. M., and Papageorgiou, L. G.
(2008). A TSP-based MILP model for medium-
term planning of single-stage continuous multiproduct
plants. Industrial & Engineering Chemistry Research,
47(20):7733–7743.
Masmoudi, O., Yalaoui, A., Ouazene, Y., and Chehade,
H. (2017). Solving a capacitated flow-shop prob-
lem with minimizing total energy costs. The Interna-
tional Journal of Advanced Manufacturing Technol-
ogy, 90(9):2655–2667.
M
´
odos., I., Kalodkin., K.,
ˇ
S
˚
ucha., P., and Hanz
´
alek., Z.
(2019). Scheduling on dedicated machines with en-
ergy consumption limit. In Proceedings of the 8th In-
ternational Conference on Operations Research and
Enterprise Systems - Volume 1: ICORES,, pages 53–
62. INSTICC, SciTePress.
Meng, L., Zhang, C., Shao, X., and Ren, Y. (2019). Milp
models for energy-aware flexible job shop scheduling
problem. Journal of Cleaner Production, 210:710 –
723.
Mitra, S., Grossmann, I. E., Pinto, J. M., and Arora,
N. (2012). Optimal production planning under
time-sensitive electricity prices for continuous power-
intensive processes. Computers & Chemical Engi-
neering, 38:171 – 184.
Mouzon, G., Yildirim, M., and Twomey, J. (2007). Opera-
tional methods for minimization of energy consump-
tion of manufacturing equipment. International Jour-
nal of Production Research, 45:4247–4271.
Shrouf, F., Ordieres-Mer
´
e, J., Garc
´
ıa-S
´
anchez, A., and
Ortega-Mier, M. (2014). Optimizing the production
scheduling of a single machine to minimize total en-
ergy consumption costs. Journal of Cleaner Produc-
tion, 67:197 – 207.
Sinha, A. and Chandrakasan, A. (2001). Dynamic power
management in wireless sensor networks. IEEE De-
sign Test of Computers, 18(2):62–74.
APPENDIX
Here, the position-based MILP model used for the
comparison is described. It was originally proposed in
(Che et al., 2017) to minimize the total tardiness and
idle energy on a single machine with a single power-
saving mode.
Reference Model
The idea of the model is to represent all possible
positions to which the individual jobs can be as-
signed. The variable representing the completion time
is linked with the position instead of the job. A set
of constraints assure that if a job is assigned to some
position, its completion time is bounded (by the dead-
line, neighboring jobs, etc.). Following decision vari-
ables are used:
x
i,l,k
Binary variable; if job J
i
is assigned to position
l on machine M
k
. then x
i,l,k
= 1, otherwise 0
y
l,k
Binary variable; if there is turn-off-on opera-
tion immediately after l-th job is processed on
machine M
k
, then y
l,k
= 1, otherwise 0
On Idle Energy Consumption Minimization in Production: Industrial Example and Mathematical Model
45

c
l,k
Integer variable; completion time of l-th job on
machine M
k
E
l,k
Continuous variable; energy consumed by ma-
chine M
k
between the completion time of k-th
job and start of (k + 1)-th job
To simplify the notation, we substitute p
i,l,k
for
∑
n
i=1
x
i,l,k
· p
i
. Also, we substitute L for {1, 2, . . . ,n}.
In the following model, T
sw
denotes the switching
time (i.e., the break-even time between the operating
and standby modes), and C
sw
stands for the switching
cost; P
on
and P
sb
represent the power consumed in the
processing mode and the standby mode, respectively.
Now, the whole model can be written as follows:
min
m
∑
k=1
n−1
∑
l=1
E
l,k
(21)
subject to
n
∑
l=1
m
∑
k=1
x
i,l,k
= 1, J
i
∈ J (22)
n
∑
i=1
x
i,l,k
≤ 1, l ∈ L, M
k
∈ M (23)
c
l,k
− p
i,l,k
≥
n
∑
i=1
x
i,l,k
· r
i
, l ∈ L, M
k
∈ M (24)
c
l,k
≤
n
∑
i=1
x
i,l,k
·
˜
d
i
+ M ·
1 −
n
∑
i=1
x
i,l,k
!
,
l ∈ L, M
k
∈ M
(25)
c
l,k
≤ c
l−1,k
+ p
i,l,k
+ y
l,k
· T
sw
, l ∈ L, M
k
∈ M
(26)
E
l,k
≥ (c
l+1,k
− c
l,k
− p
i,l,k
) · P
on
− M ·y
l,k
,
l ∈ L, M
k
∈ M
(27)
E
l,k
≥ C
sw
· y
l,k
+ (c
l+1,m
− c
l,m
− p
i,l,k
− T
sw
) · P
sb
,
l ∈ L, M
k
∈ M
(28)
To improve the performance of the model, we add
several symmetry-breaking constraints. Constraints
(29) and (30) are analogous to constraints (15) and
(16), respectively. Constraint (17) cannot be easily
integrated into the described position-based model as
it does not use the variables z
i, j
. Instead, constraints
(31) are added, which enforce assignment order from
the leftmost position to the right.
n
∑
i=1
x
i,1,k
≥
n
∑
i=1
x
i,1,k+1
, k ∈ {1, . . . , m − 1} (29)
n
∑
l=1
i
∑
k=1
x
i,l,k
= 1, i ∈ {1, . .. , min{m, n}} (30)
n
∑
i=1
x
i,l,k
≥ x
i,l+1,k
, k ∈ {1, . . . , n − 1}, M
k
∈ M
(31)
Structure of the constraints is the same as pro-
posed originally by Che et al. For a detailed descrip-
tion, we refer the reader to the original publication
(Che et al., 2017). The main adjustments, which were
made to fit our problem statements are: (i) the orig-
inal variables x
i,l
modeling the assignment were ex-
tended to x
i,l,k
; (ii) original tardinesses were omit-
ted and replaced by hard deadlines; (iii) constraint
(28) was slightly changed to work even for non-
zero standby power; (iv) several symmetry breaking
constraints were added to improve the performance.
The modified position-based model contains O(m·n
2
)
variables, which is asymptotically comparable to our
relative-order model.
ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems
46
