
Exploring Properties of the Instant Insanity Puzzle with Constraint
Satisfaction Approach
Sven L
¨
offler, Ke Liu
a
and Petra Hofstedt
Department of Mathematics and Computer Science, MINT, Programming Languages and Compiler Construction Group,
Brandenburg University of Technology Cottbus-Senftenberg, Konrad-Wachsmann-Allee 5, 03044 Cottbus, Germany
Keywords:
Constraint Programming, CSP, CSOP, Optimization, Instant Insanity Puzzle, Problem Generation, Test Case
Generation.
Abstract:
The Instant Insanity Puzzle is a challenging and interesting puzzle of combinatorial nature. The puzzle consists
of four different cubes where each face of each cube has one of the four colors red, green, white and blue.
The goal is to arrange the cubes in a tower with dimensions 1 × 1 ×4 such that on each of the four long sides
of the tower, every color appears exactly once. In this paper we pose questions derived from the puzzle, but
with increased difficulty and generality. Amongst other things, we try to find a new problem instance (a new
color assignment for the cubes) such that the number of solutions of the instant insanity puzzle is minimized
but not null. In addition, we also present a constraint programming model for the proposed questions, which
can provide the answers to our questions. The purpose of this paper is on the one hand to share our results
over the instant insanity puzzle, and on the other hand to share our gained knowledge on finding problems by
constraining the solutions of constraint satisfaction problems, which is (amongst other things) useful for the
generation of test data and teaching material.
1 INTRODUCTION
The puzzle game Instant Insanity was popularized by
the Parker Brothers Company in the late 1960s. It
has a rich history — the name Instant Insanity dates
back to the 1960s, but there were many earlier vari-
ants, released under such names as Katzenjammer,
Groceries, and The Great Tantalizer.
The Instant Insanity puzzle consists of four differ-
ent cubes where each face of each cube has one of the
four colors red, green, white and blue. The goal is to
arrange the cubes in a tower with dimensions 1 ×1×4
such that on each of the four long sides of the tower,
every color appears exactly once. Figure 1 shows a
modern version of the Instant Insanity puzzle.
The cube nets with the color assignments for each
face of the original Instant Insanity game is shown in
Figure 2. Each cube has 24 possible piece configura-
tions: 6 ways to choose the side that faces down, and
4 possible ways to rotate the visible faces.
We believe that the Instant Insanity puzzle is a
proper research object for the constraint programming
community because of its combinatorial and symmet-
rical nature. Thus, we defined the following interest-
a
https://orcid.org/0000-0002-5256-9253
Figure 1: A modern version of the Instant Insanity puzzle.
ing questions about the Instant Insanity puzzle which
pose attractive challenges:
1. Can we find a suitable CSP, which solves the
original problem using constraint programming?
In this paper, we call all solutions of the
original problem an all different Instant
Insanity solution (ADIIS).
2. Do the cubes of the original problem allow to find
a tower where each of the long sides of the tower
use the same color, such that one long side is
green, one red, one blue and one white? In this
Löffler, S., Liu, K. and Hofstedt, P.
Exploring Properties of the Instant Insanity Puzzle with Constraint Satisfaction Approach.
DOI: 10.5220/0008880403310338
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 331-338
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
331

paper, we call each solution of this kind an all
equal Instant Insanity solution (AEIIS).
If there is no such solution, can we then find a
set of cubes which has solutions of both kinds:
ADIIS and AEIIS?
3. Can we find a set of cubes, which has the lowest
number of ADIIS but at least one?
4. Can we find a set of cubes, which has the lowest
number of AEIIS but at least one?
5. Can we find a set of cubes, which has the lowest
number of ADIIS plus AEIIS but at least one of
ADIIS and one of AEIIS?
Figure 2: The cube nets with collor assignments of the In-
stant Insanity puzzle.
Remark 1: The questions three, four and five are mo-
tivated by finding a new puzzle, which is as difficult
as possible. We assume that such a problem is more
complicated if the ratio of solutions by possible com-
binations is as small as possible.
Remark 2: For the questions two to five, we have the
additional constraint, that each cube should contain at
least each color once.
Remark 3: The questions two to five assume that we
find a possibility to define constraints over the solu-
tions of a CSP. We think that such an approach can
be useful in different areas like the development of
games or logic puzzles, in test case generation or in
the generation of educational material.
The rest of this paper is organized as follows. In
Section 2, we give a brief introduction into constraint
programming. Afterwards, in Section 3, we describe
our constraint models to solve the posed questions and
present the experimental results. In Section 4 we con-
clude and give a brief overview on future works.
2 PRELIMINARIES
In this section we give some basic definitions and con-
cepts of constraint programming (CP) and the relevant
constraints for the modelling of the Instant Insanity
puzzle.
Constraint programming is a powerful technique
to tackle (generally NP-hard) combinatorial prob-
lems. Since the 2000s, constraint programming is also
used for test case generation (Aichernig and Salas,
2005; Degrave et al., 2009; Caballero et al., 2010;
Wotawa et al., 2011; Ernsting et al., 2012). We like to
use constraint programming in a similar way for cre-
ating new tasks during we define constraints over the
solutions of the searched tasks.
We consider constraint satisfaction problems
(CSPs), which are defined in the following way.
CSP (Dechter, 2003) A constraint satisfaction
problem (CSP) is defined as a 3-tuple P = (X,D,C)
with X = {x
1
,x
2
,...,x
n
} is a set of variables, D =
{D
1
,D
2
,..., D
n
} is a set of finite domains where D
i
is the domain of x
i
and C = {c
1
,c
2
,...,c
m
} is a set of
constraints covering between one and all variables in
X.
Each constraint c
i
is a relation defined over a sub-
set of the variables X and restricts the values that can
be simultaneously assigned to these variables. A so-
lution of a CSP P is a complete instantiation satisfy-
ing all constraints of the CSP P. Further we define
constraints required to describe the Instant Insanity
puzzle. Let a CSP P = (X,D,C) and a subset X
0
of
variables X of the CSP P be given.
The arithm constraint describes an arithmetic re-
lation between two (x
i
,x
j
∈ X
0
) or three (x
i
,x
j
,x
k
∈
X
0
) variables (see Equation 1).
arithm(x
i
,ℜ,x
j
) := x
i
ℜ x
j
arithm(x
i
,,x
j
,ℜ,x
k
) := x
i
x
j
ℜ x
k
(1)
The symbol ℜ is an operator in {=, <, >, 6=, ≤, ≥}
and the symbol is an operator in
{
+,−,∗,/
}
.
The allDifferent constraint is a prime example for
a global constraint. For an ordered set of variables
{x
1
, x
2
, . . . , x
n
} = X
0
it guarantees that each variable
has a different value (see Equation 2).
allDi f f erent(X
0
) := x
i
6= x
j
∀x
i
,x
j
∈ X
0
,i 6= j (2)
It outlines two of the main advantages of global
constraints. On one hand, using the allDi f f erent
constraint simplifies the modelling process only one
allDi f f erent constraint must be posted instead of
many pairwise not equal constraints and on the other
hand the allDi f f erent constraint allows to use more
effective propagation algorithms (L
´
opez-Ortiz et al.,
2003) as the pairwise not equal constraints. Anal-
ogously to the allDi f f erent constraint there is an
allEqual constraint, which requires that every vari-
able of a sequence of variables X
0
must have the same
value.
The count
2
constraint is a common global con-
straint, where for an ordered set of variables X
0
= {x
1
,
2
This paper follows the naming convention of Choco
solver. Other solvers might use a different name for the
same constraint.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
332

x
2
, . . . , x
n
} the variable occ ∈ X with domain D
occ
=
{occ
min
,...,occ
max
} denotes the admissible number
of occurrences of the value v ∈ N in X
0
(see Equation
3).
count(X
0
,occ,v) := (
∑
x∈X
0
(
0 x 6= v
1 x = v
) ∈ D
occ
(3)
The element constraint guarantes for a sequence
of variables {x
1
, x
2
, . . . , x
n
} = X
0
, that the ith variable
must be equal to a variable x
0
∈ X (see Equation 4).
element(x
0
,X
0
,i) := X
0
[i] == x
0
(4)
The table constraint is also one of the most fre-
quently used constraints in practice. For an ordered
subset of variables X
0
= {x
i
,...,x
j
}, a positive (or
negative) table constraint defines that any solution of
the CSP P must (not) be explicitly assigned to a tuple
of a given tuple list T , which consists of the allowed
(disallowed) combinations of values for X
0
(see Equa-
tion 5).
table(X
0
,T ) := {(x
i
,...,x
j
) |
x
i
∈ D
(x
i
)
,...,x
j
∈ D
(x
j
)
} ∈ T
(5)
The sum constraint is also a common global con-
straint, where the sum of a sequence of variables
(x
i
,...,x
j
) must be in relation ℜ ∈ {=, <, >, 6=,≤,≥}
to a variable s ∈ X (see Equation 6).
sum(x
i
,...,x
j
,ℜ,s) := x
i
+ ... + x
j
ℜ s (6)
The regular constraint (Hellsten et al., 2004; Pe-
sant, 2001; Pesant, 2004) is the last global constraint
we present in this short selection. For the regular
constraint, we briefly need to show the definition of
a deterministic finite automaton (DFA) (Hopcroft and
Ullman, 1979).
A deterministic finite automaton (DFA) is a quin-
tuple M = (Q, Σ, δ, q
0
, F), where Q is a finite set of
states, Σ is the finite input alphabet, δ is a transforma-
tion function Q ×Σ → Q, q
0
∈ Q is the initial state and
F ⊆ Q is the set of final or accepting states. A word
w ∈ Σ
∗
is accepted by M, i.e. w ∈ L(M), if the cor-
responding DFA M with the input w stops in a final
state f ∈ F (Hopcroft and Ullman, 1979).
The regular constraint obtains a DFA M = (Q,
Σ, δ, q
0
, F) and an ordered subset of variables X
0
=
{x
1
,...,x
n
} ⊆ X, with D(x
i
) ⊆ Σ for 1 ≤ i ≤ n as in-
put and guarantees that every sequence d
1
◦ ... ◦ d
n
of
values for x
1
,...,x
n
must be a word of the regular lan-
guage recognized by the DFA M, where ◦ is the con-
catenation of two words (Pesant, 2004) (see Equation
7).
regular(X
0
,M) = {(d
1
,...,d
n
)|∀i d
i
∈ D
i
,
d
1
◦ d
2
◦ ... ◦ d
n
∈ L(M)}
(7)
We refer to (Dechter, 2003; Rossi et al., 2006;
Lecoutre, 2009) for more comprehensive and pro-
found introduction to constraint programming.
3 THE CONSTRAINT
PROGRAMMING MODELS
In this section we explain the constraint models we
used to answer the questions 1 to 5 and present our
results.
3.1 A Model for the ADIIS and AEIIS
Problem
To solve problem 1, we first should identify the
decision variables for the CSP model. Then we
impose constraints on these variables based on the
problem definition. Focusing on the Instant Insan-
ity puzzle it has 4 cubes with 6 faces each, we
use a two-dimensional array of integer variables
X = {{x
1,1
,...,x
1,6
},...,{x
4,1
,...,x
4,6
}} to represent
the colors of each side of each cube, each of which has
domain d
i, j
= {0,1,2,3}|∀i ∈ {1,...,4}, j ∈ {1,...,6}
representing the four different colors.
Suppose that we number the sides as depicted in
Fig. 3. Then there are 24 possible piece configura-
tions: 6 ways to choose the side that faces down, and
4 possible ways to rotate the visible faces. These 24
piece configurations are also listed in Fig. 3.
Therefore, each sequence of variables which de-
scribes one cube ({x
i,1
,...,x
i,6
}∀i ∈ {1, ..., 4}) must
satisfy one of these 24 possible piece configurations.
It is not possible to use this configurations directly, but
we can substitute the values 1 to 6 of the configura-
tions with the numbers 1 to 4, which represent the col-
ors (1 = RED, 2 = BLUE, 3 = GREEN, 4 = WHITE)
of the cubes
3
. Using the numeration of Fig. 3 and
the color net from Fig. 2, the puzzle has the following
color sequences (C
1
,...,C
4
) for the 4 cubes:
1. RED,RED,GREEN,W HIT E,BLUE,W HIT E
2. BLUE,RED,WHIT E,BLUE,GREEN,W HIT E
3. GREEN,RED,W HIT E,GREEN,BLUE,BLU E
4. W HIT E,RED,GREEN,RED,BLUE,RED.
Let be T the 24 × 6 matrix which represents the 24 6-
tuples in Fig. 3. Therefore, the table constraint with
matrix T
0
and variables {x
i,1
,...,x
i,6
}∀i ∈ {1,...,4}
guarantees that each face of the cube i has a color,
3
In the rest of the paper, we use the numerical values
1, 2, 3, and 4 to represent the corresponding colors RED,
BLUE, GREEN and WHITE.
Exploring Properties of the Instant Insanity Puzzle with Constraint Satisfaction Approach
333
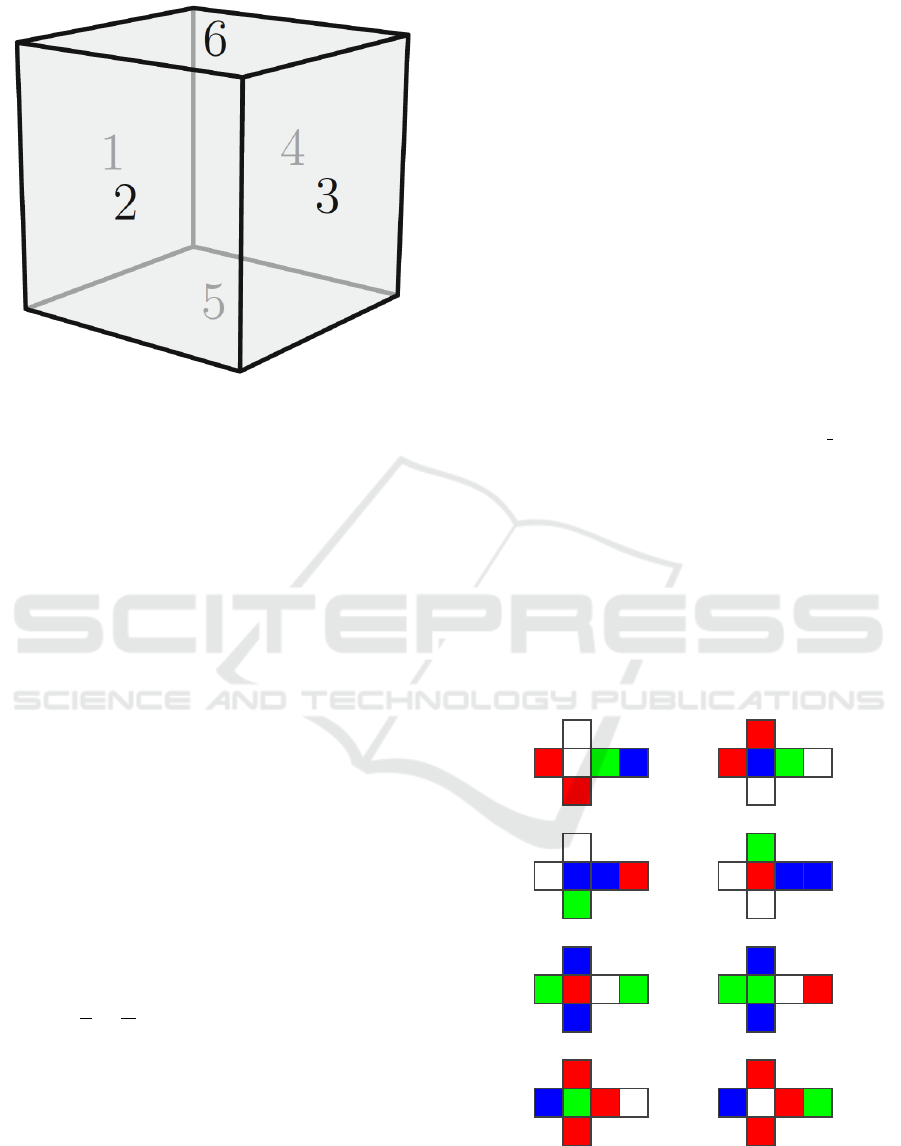
(1,2,3,4,5,6), (1,5,3,6,4,2), (1,4,3,2,6,5), (1,6,3,5,2,4),
(2,3,4,1,5,6), (2,5,4,6,1,3), (2,1,4,3,6,5), (2,6,4,5,3,1),
(3,2,1,4,6,5), (3,5,1,6,2,4), (3,4,1,2,5,6), (3,6,1,5,4,2),
(4,3,2,1,6,5), (4,6,2,5,1,3), (4,1,2,3,5,6), (4,5,2,6,3,1),
(5,2,6,4,3,1), (5,3,6,1,4,2), (5,4,6,2,1,3), (5,1,6,3,2,4),
(6,2,5,4,1,3), (6,3,5,1,2,4), (6,4,5,2,3,1), (6,1,5,3,4,2)
Figure 3: Labels for each of the faces on a cube.
which is reachable by rotating the cube i along the x-,
y-, or z-axis (see Eq. 8).
table({x
i,1
,...,x
i,6
},T
i
)∀i ∈ {1,...,4} (8)
Where table T
i
is defined by the possible piece config-
urations T and the given colors C
1
,...C
4
of the Instant
Insanity puzzle (see Eq. 9).
T
i
x,y
= C
i
[T
x,y
]
∀i ∈ {1,...,4},x ∈ {1,...,24},y ∈ {1,...,6}
(9)
Remark 4: Using the table constraint like
presented before, leads to a strict cube order
C
1
,C
2
,C
3
,C
4
, which is not given in the game. The
patterns we try to find (ADIIS or AEIIS) are indepen-
dent from the cube order. Thus, a solution for the
given variable order is always also a solution for ev-
ery other permutation of the 4 cubes. Doing this re-
duces the number of solutions and the search space
by factor
1
4!
=
1
24
, which leads to a speed up in the so-
lution process. If all solutions are searched, then the
real solution number is the number of detected solu-
tions times 24. We call such a constraint a symmetry
breaking constraint.
After constraining the color side dependencies of
the cubes, it is necessary to define the target require-
ment. For ADIIS, every side of a tower must use ev-
ery color once. Thus all equally positioned sides of
the different cubes must take distinct colors. There-
fore, (x
1,i
,x
2,i
,x
3,i
,x
4,i
∀i ∈ {1,2, 3, 4}) must satisfy
the allDifferent constraint, given by Eq. 10:
allDifferent(x
1,i
,x
2,i
,x
3,i
,x
4,i
)∀i ∈ {1,2,3, 4} (10)
For the AEIIS problem we need instead of the
constraint given by Eq. 10 an allEqual constraint
(see Eq. 11) for all variables x
1,i
,x
2,i
,x
3,i
,x
4,i
∀i ∈
{1,2,3,4}.
allEqual(x
1,i
,x
2,i
,x
3,i
,x
4,i
)∀i ∈ {1,2,3, 4} (11)
Results
After presenting our CSP model for finding an ADIIS
and an AEIIS, we want to show our results.
All the experiments (for all 5 problem instances)
are set up on a DELL laptop with an Intel i7-
4610M CPU, 3.00GHz, with 16 GB RAM, 1600
MHz DDR3 and running under Windows 7 profes-
sional with service pack 1. The algorithms are im-
plemented in Java under JDK version 1.8.0 191 and
Choco Solver (Prud’homme et al., 2016). We used the
DowOverW Deg search strategy which is explained in
(Boussemart et al., 2004) and is used as the default
search strategy in the Choco Solver (Prud’homme
et al., 2016).
For the ADIIS problem instance, we could find all
solutions in less than one second. There are eight so-
lutions in which every four solutions are equivalent
under rotation of the tower around the z-axis. The
two real different solutions (with respect to rotation)
are shown in Figure 4.
Figure 4: The two different solutions of the Instant Insanity
puzzle.
For the AEIIS problem instance the Choco Solver
can detect that no solution exists. This leads us to the
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
334

second part of question two; can we find a set of cubes
which has solutions of both ADIIS and AEIIS?
3.2 A Model for Finding Cubes with
ADIIS and AEIIS
For finding cubes that have at least one ADIIS and
one AEIIS, we have to remodel our CSP significantly.
Finally, again, we only need for each cube, for each
side a color assignment: RED, BLUE, GREEN or
WHITE. But for this, we have to respect that a ro-
tation of the cubes should have an ADIIS and at least
one other rotation an AEIIS. So we formulate con-
straints over the solutions of our original problem.
Again, we use a two-dimensional array of inte-
ger variables X = {{x
1,1
,...,x
1,6
},...,{x
4,1
,...,x
4,6
}}
to represent the colors of each side of each cube,
each of which has domain d
i, j
= {0,1,2,3}|∀i ∈
{1,...,4}, j ∈ {1, ..., 6} representing the four different
colors. We additionally post constraints that guaran-
tee, that each cube has each color at least one time
(see Equation 12).
count({x
i,1
,...,x
i,6
},{1,2,3},v)
∀i ∈ {1,...,4},v ∈ {1,...,4}
(12)
The difficulty is that this time we have no input
tables T
i
for our table constraints in Eq. 8. We only
know the structure of the tables T
i
but not the con-
crete content. We know that T
i
must satisfy the rota-
tions shown in Figure 3, which gives us the following
information:
1. The table T
i
is a 24 × 6 matrix.
2. All 1s must be substituted by the same single color
RED, BLUE, GREEN or WHITE. The same is
valid for the other numbers 2 to 6.
3. If the color assignment for the first row of the ma-
trix is clarified, then all other rows can be set in-
stantly as consequence of this, because each num-
ber 1 to 6 is assigned to exactly one color (RED,
BLUE, GREEN or WHITE).
Because we don’t know the concrete values of the
matrices T
i
, but we know, that each T
i
is a 24 × 6
matrix with values 1 to 4. We represent them as two-
dimensional arrays of integer variables, where the first
row of each matrix is the sequence of variables repre-
senting the ith cube T
i
1
= {x
i,1
,...,x
i,6
}. Each other
entry in T
i
is a copy of one of the variables in the
first line of T
i
, where T
i
x,y
= x
i,T
x,y
∀i ∈ {1,...,4},
x ∈ {2,...,24}, y ∈ {1,...,6}, where T is the possible
piece configuration given in Figure 3.
Next we have to formulate one solution of the
newly formulated tables T
i
. For this we create 16
new variables S
ADIIS
= {s
ADIIS
x,y
|∀x ∈ {1,...,4},y ∈
{1,...,4}}, where x represents the cube and y the side
of the cube. The sides 5 (bottom side) and 6 (top side)
of each cube are not important for the solution of the
problem so that we do not consider them here.
For each cube i must exist one integer variable
index with D
index
= {1,...24} such that all values of
the variables s
ADIIS
i,∗
are equal to the values of T
i
index,∗
.
The element constraints shown in Equation 13 realize
this.
element(s
ADIIS
i,y
,T
i
∗,y
,index) ∀y ∈ {1,...,4} (13)
The variables S
ADIIS
represent a valid cube con-
figuration (because of the element constraints), but
not necessarily an ADIIS of the problem. To get
an ADIIS it is necessary to post the allDi f f erent
constraints shown in Equation 10 on the variables
s
ADIIS
1,i
,s
ADIIS
2,i
,s
ADIIS
3,i
,s
ADIIS
4,i
instead of the variables
x
1,i
,x
2,i
,x
3,i
,x
4,i
.
After we guarantee that a solution for ADIIS ex-
ists, we have to do the same for AEIIS. So we cre-
ate 16 new integer variables S
AEIIS
= {s
AEIIS
x,y
|∀x ∈
{1,...,4},y ∈ {1,...,4}} and an index variable for
each cube i with domain D
index
= {1,...24} such that
all values of the variables s
AEIIS
i,∗
are equal to the values
of T
i
index,∗
. It is only necessary to change the S
ADIIS
variables with the S
AEIIS
variables in the element con-
straints shown in Equation 13 to realize this.
Analogously to ADIIS, it is only necessary to post
the allEqual constraints shown in Equation 11 on
the variables s
AEIIS
1,i
,s
AEIIS
2,i
,s
AEIIS
3,i
,s
AEIIS
4,i
instead of the
variables x
1,i
,x
2,i
,x
3,i
,x
4,i
to get an AEIIS.
Results
Solving the newly created CSP delivers us a huge
number of cube combinations which have an ADIIS
and an AEIIS. However because the Instant Insanity
puzzle is interesting because of its difficulty, we also
want an cube configuration which has an ADIIS and
an AEIIS but is also difficult to solve. We expect that
such a puzzle is hard to solve if it has only a small
number of solutions. This leads us to our questions 3,
4 and 5. Can we find a cube configuration such that it
has a minimum number of ADIIS, a minimum num-
ber of AEIIS or a minimum number of ADIIS plus
AEIIS?
Exploring Properties of the Instant Insanity Puzzle with Constraint Satisfaction Approach
335

3.3 A Model for Finding Cubes with a
Minimum Number of ADIIS and
AEIIS
For counting and minimizing the number of solutions
we create two automatons, which represent all pos-
sible ADIIS and AEIIS without respect to the cube
rotations. Then we create meta constraints, which
represent these automatons and count the number
of accepting paths inside them considering the cube
rotations. The index variables and the S
AEIIS
re-
spectively the S
ADIIS
variables, and the element con-
straints, shown in Equation 13 are no longer needed.
The automaton for the AEIIS over the variables
X
AEIIS
= {x
1,1
,x
2,1
,x
3,1
,x
4,1
,x
1,2
,...,x
4,4
} is created
by clever intersections of singleton automatons M
eq
which accept the words {0000, 1111,2222,3333}.
For this we create four M
eq
i
automatons over the
variables {x
i,1
,x
i,2
,x
i,3
,x
i,4
} ∀i ∈ {1,2,3,4}, fill them
with the missing variables of the variable sequence
X
AEIIS
in a way that the missing variables can have
any value of their domain, and intersect these four
M
eq
i
automatons to one M
AEIIS
automaton. The au-
tomaton M
ADIIS
for the ADIIS can be created analo-
gously.
For the next step we need count variables X
c
=
{x
i,a,b,c,d
∀i,a,b,c,d ∈ {1, 2, 3, 4}} for each cube i
and each combination of colors for the four visible
sides {a, b, c,d} with domains {0,1,2,3, 4}. The vari-
ables represent how often each sequence of colors
{a,b,c,d} is included in the T
i
rotation matrix of each
cube i. Because of the structure of the rotation matri-
ces T
i
, each color sequence can occur between 0 and 4
times. We created a regular constraint for each cube i
which counts the equal sequences of colors {a,b,c,d}
and sets the variables x
i,a,b,c,d
to the corresponding
values.
In the next step we reduce all paths in M
ADIIS
(re-
spectively M
AEIIS
) of the form q a
−→
q
0
b
−→
q
00
c
−→
q
000
d
−→
q
0000
to the path qabcd
−−→
q
0000
, where abcd is the concatena-
tion of elements of the domain values of the vari-
able sequence {x
1,1
,...,x
4,1
}. We repeat this reduc-
tion for the paths over the variables {x
1,i
,...,x
4,i
} ∀i ∈
{2,3,4}. The result is an equivalent automaton
M
ADIIS
short
(respectively M
AEIIS
short
) which represents the
same words, with the difference that the inputs are not
singleton colors {RED, BLUE, GREEN, WHITE}
but instead color sequences of size four.
Figure 5 shows an example for clarifying the re-
duction process. For simplification only each two in-
puts are reduced to one.
Now we create meta constraints which combine
the automatons M
ADIIS
short
(respectively M
AEIIS
short
) with the
q
1
q
2
q
3
q
4
0
q
5
0
1
q
6
1
0,1
q
7
1
⇒
q
1
q
2
q
3
q
6
01
00,01
10,11
q
7
01
11
Figure 5: An example for the reducing process of an au-
tomaton.
count variables X
c
. For each cube i, each value abcd
in the automaton M
ADIIS
short
(respectively M
AEIIS
short
) cor-
responds to the variable x
i,a,b,c,d
, where the value of
x
i,a,b,c,d
indicates how many cube rotations in T
i
have
the value sequence abcd.
Thus, each path in M
ADIIS
short
(respectively M
AEIIS
short
),
from the start node to the end node with val-
ues a
1
b
1
c
1
d
1
,a
2
b
2
c
2
d
2
,a
3
b
3
c
3
d
3
,a
4
b
4
c
4
d
4
, where
the value of all corresponding count variables
(x
1,a
1
,b
1
,c
1
,d
1
,x
2,a
2
,b
2
,c
2
,d
2
,x
3,a
3
,b
3
,c
3
,d
3
,x
4,a
4
,b
4
,c
4
,d
4
) is
not null, is exactly an ADIIS (respectively AEIIS)
of the Instant Insanity problem with four cubes,
where the six sides have the color assignment
{x
i,1
,...,x
i,6
∀i ∈ {1,2,3,4}}. Furthermore, the re-
sult of the multiplication of the corresponding count
variables (x
1,a
1
,b
1
,c
1
,d
1
∗ x
2,a
2
,b
2
,c
2
,d
2
∗ x
3,a
3
,b
3
,c
3
,d
3
∗
x
4,a
4
,b
4
,c
4
,d
4
) is exactly the number of possible cube
rotations which reach this solution.
For the enumeration of all solutions, we create
several constraints shown in Equation 14. For each
state q
n
of the automaton M
ADIIS
short
a variable x
n
is cre-
ated, which counts the paths from the initial state of
the automaton to q
n
. The number of possibilities is
calculated by the sum of the value of each predeces-
sor x
pre
multiplied by the number of cube rotations
x
i,a,b,c,d
, which represents the path from the predeces-
sor node x
pre
to the current node q
n
with the value
abcd. The variable x
initial
, which represents the initial
state q
initial
is set to 1. All other values are then calcu-
lated by the given constraints. The number of possible
solutions is then exactly the value of the variable x
f inal
which represents the singleton final state q
f inal
.
∀ States q
n
∈ {M
ADIIS
short
} :
x
n
=
∑
{x
pre
∗ x
i,a,b,c,d
| ∀a,b, c,d,
where q
pre
abcd
−−→
q
n
}
(14)
For example, if the color assignments RED, RED,
BLUE, GREEN, W HIT E, BLUE and RED, RED,
BLUE, GREEN, BLU E, W HITE are in T
1
, then
the count variable x
1,1,2,3,4
has value 2 and there ex-
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
336

ists a constraint q
initial
1234
−−→
q
n
with x
initial
= 1, x
n
=
x
initial
∗ x
1,1,2,3,4
= 1 ∗ 2 = 2, which set x
n
to 2.
For minimizing the number of ADIIS, we have to
minimize the x
f inal
variable. For minimizing the num-
ber of AEIIS, we have to minimize the x
f inal
vari-
able, which results from constraints shown in Equa-
tion 14, where the M
ADIIS
short
automaton is substituted
by the M
AEIIS
short
automaton. For finding the minimum
number of ADIIS plus AEIIS, we have to create the
constraints shown in Equation 14 for both automatons
(M
ADIIS
short
and M
AEIIS
short
) and minimize the sum of both
final states. In all cases we allow only values greater
than null for the final states.
Result
The good news is that we were able to find solutions
for all three instances. We found in less than 5 sec-
onds a cube coloring which has only four ADIIS. In
less than 3 seconds we found a cube coloring, which
has only two AEIIS. In less than 4 seconds we found
a cube coloring, which has only 24 ADIIS and two
AEIIS. The given results are the number of solu-
tions after removing equivalent solutions, which re-
sult from the rotation of the whole tower around the
z-axis.
The bad news is that we unfortunately could not
show that these are the minimum numbers of solu-
tions after running the programs for two days. Never-
theless considering the found results, we can see that
these are at least very good solutions, and maybe the
best in case of AEIIS, and ADIIS plus AEIIS.
4 CONCLUSION AND FUTURE
WORK
By means of the constraint programming approach,
we found solutions for the original Instant Insanity
problem and have proved that no AEIIS exists. How-
ever, we were not able to answer the rest of the ques-
tions posed in the Introduction (cf. Sec. 1), although
some feasible solutions were found. We expect that
we can also find the minimized solutions for our ques-
tions 3, 4 and 5 with our given CSP after including
some optimizations like using parallel computing and
minimizing the number of used variables and con-
straints, especially the ones used in Equation 14.
The real benefits of this paper are the abstractions
of the table and the regular constraints, to find a prob-
lem of a defined kind with special requirements for
the solutions. Examples for these special require-
ments are the demand to have solutions of one or
many special kinds (in this case ADIIS and AEIIS)
or to have a minimum number of solutions. We ex-
pect that this knowledge can be very profitable in the
test data generation, where we want to cover the most
critical parts with the lowest number of tests, or in
the digitization in teaching where we are always in-
terested in task generation and creation of running ex-
amples.
In future work we will increase the problem de-
scription by generalizing the number of cubes from 4
to n according to (Demaine et al., 2013). This prob-
lem is then called the Cube Stacking Problem and it
has been demonstrated, that it is np-complete. This
allow us to experimentally evaluate the scalability of
our encoding with respect to the number of cubes that
we consider.
An other generalization would be to use k-gonal
prism pieces and not just cubes for stacking. A study
of this generalization is also given in (Demaine et al.,
2013) and a CP-encoding will may be useful to solve
these instances.
REFERENCES
Aichernig, B. K. and Salas, P. A. P. (2005). Test case gener-
ation by OCL mutation and constraint solving. In Fifth
International Conference on Quality Software (QSIC
2005), 19-20 September 2005, Melbourne, Australia,
pages 64–71.
Boussemart, F., Hemery, F., Lecoutre, C., and Sais, L.
(2004). Boosting systematic search by weighting con-
straints. In de M
´
antaras, R. L. and Saitta, L., editors,
Proceedings of the 16th Eureopean Conference on Ar-
tificial Intelligence, ECAI’2004, including Prestigious
Applicants of Intelligent Systems, PAIS 2004, Valen-
cia, Spain, August 22-27, 2004, pages 146–150. IOS
Press.
Caballero, R., Garc
´
ıa-Ruiz, Y., and S
´
aenz-P
´
erez, F. (2010).
Applying constraint logic programming to SQL test
case generation. In Functional and Logic Program-
ming, 10th International Symposium, FLOPS 2010,
Sendai, Japan, April 19-21, 2010. Proceedings, pages
191–206.
Dechter, R. (2003). Constraint processing. Elsevier Morgan
Kaufmann.
Degrave, F., Schrijvers, T., and Vanhoof, W. (2009). To-
wards a framework for constraint-based test case gen-
eration. In Logic-Based Program Synthesis and Trans-
formation, 19th International Symposium, LOPSTR
2009, Coimbra, Portugal, September 2009, Revised
Selected Papers, pages 128–142.
Demaine, E. D., Demaine, M. L., Eisenstat, S., Morgan,
T. D., and Uehara, R. (2013). Variations on instant
insanity. In Space-Efficient Data Structures, Streams,
and Algorithms.
Ernsting, M., Majchrzak, T. A., and Kuchen, H. (2012). Dy-
namic solution of linear constraints for test case gen-
eration. In Sixth International Symposium on Theoret-
Exploring Properties of the Instant Insanity Puzzle with Constraint Satisfaction Approach
337

ical Aspects of Software Engineering, TASE 2012, 4-6
July 2012, Beijing, China, pages 271–274.
Hellsten, L., Pesant, G., and van Beek, P. (2004). A do-
main consistency algorithm for the stretch constraint.
In Wallace, M., editor, Principles and Practice of
Constraint Programming - CP 2004, volume 3258 of
Lecture Notes in Computer Science, pages 290–304.
Springer.
Hopcroft, J. E. and Ullman, J. D. (1979). Introduction
to Automata Theory, Languages and Computation.
Addison-Wesley.
Lecoutre, C. (2009). Constraint Networks: Techniques and
Algorithms. Wiley.
L
´
opez-Ortiz, A., Quimper, C., Tromp, J., and van Beek,
P. (2003). A fast and simple algorithm for bounds
consistency of the alldifferent constraint. In Gottlob,
G. and Walsh, T., editors, IJCAI-03, Proceedings of
the Eighteenth International Joint Conference on Ar-
tificial Intelligence, Acapulco, Mexico, August 9-15,
2003, pages 245–250. Morgan Kaufmann.
Pesant, G. (2001). A filtering algorithm for the stretch con-
straint. In Walsh, T., editor, Principles and Practice of
Constraint Programming - CP 2001, volume 2239 of
Lecture Notes in Computer Science, pages 183–195.
Springer.
Pesant, G. (2004). A regular language membership con-
straint for finite sequences of variables. In Wallace,
M., editor, Principles and Practice of Constraint Pro-
gramming - CP 2004, volume 3258 of Lecture Notes
in Computer Science, pages 482–495. Springer.
Prud’homme, C., Fages, J.-G., and Lorca, X. (2016).
Choco Documentation. TASC, INRIA Rennes, LINA
CNRS UMR 6241, COSLING S.A.S. http://www.
choco-solver.org/, last visited 2017-06-20.
Rossi, F., Beek, P. v., and Walsh, T. (2006). Handbook of
Constraint Programming. Elsevier, Amsterdam, First
edition.
Wotawa, F., Nica, S., and Nica, M. (2011). Debugging
and test case generation using constraints and muta-
tions. In Proceedings of the Ninth Workshop on Intel-
ligent Solutions in Embedded Systems, WISES 2011,
Regensburg, Germany, July 7-8, 2011, pages 95–100.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
338
