
Radially Distorted Planar Motion Compatible Homographies
Marcus Valtonen
¨
Ornhag
Centre for Mathematical Sciences, Lund University, Lund, Sweden
Keywords:
Planar Motion, Homography, Radial Distortion, Polynomial Solver, Trajectory Recovery, Visual Odometry.
Abstract:
Fast and accurate homography estimation is essential to many computer vision applications, including scene
degenerate cases and planarity detection. Such cases arise naturally in man-made environments, and failure
to handle them will result in poor positioning estimates. Most modern day consumer cameras are affected
by some level of radial distortion, which must be compensated for in order to get accurate estimates. This
often demands calibration procedures, with specific scene requirements, and off-line processing. In this paper
a novel polynomial solver for radially distorted planar motion compatible homographies is presented. The
proposed algorithm is fast and numerically stable, and is proven on both synthetic and real data to work well
inside a RANSAC loop.
1 INTRODUCTION
In many computer vision applications it is desired
to find a homography between two images. With-
out imposing any prior knowledge of the model, or
intrinsic parameters, a general homography can be
estimated using a minimal of four point correspon-
dences (Hartley and Zisserman, 2004). If any of the
intrinsic parameters are known, or other model con-
straints are enforced, the number of needed point cor-
respondences decrease, however, encoding these ge-
ometric properties may result in non-linear systems
of polynomial equations. Solving such systems suf-
ficiently fast, with an acceptable numerical precision,
often involves methods from computational algebraic
geometry (Cox et al., 2005).
Planar motion models are a well-studied field in
computer vision. While several authors have con-
sidered restricted models, requiring various calibra-
tion procedures (Ort
´
ın and Montiel, 2001; Chen and
Liu, 2006; Hajjdiab and Lagani
`
ere, 2004), the general
case, including the assumption of a constant—and
unknown—overhead tilt, was introduced in (Liang
and Pears, 2002). This model was also considered
by (Wadenb
¨
ack and Heyden, 2013; Wadenb
¨
ack and
Heyden, 2014; Zienkiewicz and Davison, 2015).
Many planar motion compatible navigation sys-
tems are based on estimating the homographies for
consecutive views. Instead of eight degrees of free-
dom, as in the general case, planar motion compatible
homographies only have five—two overhead tilt an-
gles (assumed to be constant), one rotational angle,
and two translational components. The standard pro-
cedure for estimating homographies is usually divided
in extracting and matching keypoints, followed by
estimating putative homographies in a robust frame-
work. Typically, this is done using RANSAC in or-
der to discard outliers introduced in the matching step.
The probability of selecting a set of points containing
only inliers depends on the amount of points selected,
and therefore it is advantageous to make this choice
minimal.
In this paper we consider the case of planar motion
with a constant overhead tilt and unknown radial dis-
tortion. Such a setup is common for Visual Odometry
(VO) in man-made environments, where the goal is to
estimate the position of a vehicle, on which the cam-
era is mounted. We propose a novel four point homo-
graphy solver, which is suitable for real-time applica-
tions and numerically stable. The solver is compared
to an existing solver and show an increase in perfor-
mance on both synthetic and real data. Furthermore,
we show how the solver can be incorporated in a VO
pipeline for indoor navigation.
2 RELATED WORK
Consider a pair of point correspondences x
x
x ↔
ˆ
x
x
x, on
a common scene plane, related by a homography H
H
H.
In homogeneous coordinates, let x
x
x = (x, y, w)
T
and
ˆ
x
x
x = ( ˆx, ˆy, ˆw)
T
, then λ
ˆ
x
x
x = H
H
Hx
x
x, for some scalar λ. Left-
280
Örnhag, M.
Radially Distorted Planar Motion Compatible Homographies.
DOI: 10.5220/0008893802800288
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 280-288
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

multiplying this relation with the cross-product ma-
trix [
ˆ
x
x
x]
×
gives [
ˆ
x
x
x]
×
H
H
Hx
x
x = 0
0
0, or, equivalently,
0
0
0 − ˆwx
x
x
T
ˆyx
x
x
T
ˆwx
x
x
T
0
0
0 − ˆxx
x
x
T
− ˆyx
x
x
T
ˆxx
x
x
T
0
0
0
h
h
h
1
h
h
h
2
h
h
h
3
= 0
0
0, (1)
where h
h
h
T
k
is the k:th row of the homography ma-
trix H
H
H. This formulation conveniently eliminates the
scale parameter λ, while introducing two linearly in-
dependent equations, since the cross-product matrix
is of rank 2. These are known as the Direct Linear
Transform (DLT) equations. From this formulation,
using four point correspondences, the minimal prob-
lem reduces to finding the one-dimensional null space
of H
H
H. If the homography is constrained further, as
in the case of planar motion, this approach can still
be used; however, the null space is no longer one-
dimensional. The problem then translates into find-
ing the corresponding null space basis coefficients.
In (Wadenb
¨
ack et al., 2016) the authors showed that
it was possible to construct a minimal solver for the
general planar motion homography by using this ap-
proach, in which a polynomial system of 11 quartic
equations in four variables are solved. Non-minimal
relaxations of the same problem was studied in (Val-
tonen
¨
Ornhag, 2019), and tested in a VO framework
for planar motion.
There are two common approaches for modeling
radial distortion, the Brown–Conrady model (Brown,
1966), and the division model introduced in (Fitzgib-
bon, 2001). The latter has the benefit of being suf-
ficiently good with fewer parameters than the for-
mer. We will exclusively use the division model
with a single distortion parameter λ, in which the
distorted (measured) image points are denoted x
x
x
i
=
x
i
y
i
1
T
, and related to the undistorted image
points x
x
x
u
i
, by the relation
x
x
x
u
i
= f (x
x
x
i
,λ) =
x
i
y
i
1 + λ(x
2
i
+ y
2
i
)
. (2)
where the distortion center is assumed to be at the
center of the image, which is also the origin of our se-
lected coordinate system. Since the distortion param-
eter only appears in the homogeneous coordinates, the
DLT equations (1) still hold true, with the adjustment
[ f (
ˆ
x
x
x
i
,λ)]
×
H
H
H f (x
x
x
i
,λ) = 0
0
0, (3)
for two point correspondences x
x
x
i
↔
ˆ
x
x
x
i
. A minimal
solver for the case of radially distorted homographies
were presented in (Kukelova et al., 2015), in which
the authors incorporated the radial distortion using
the modified DLT equations (3). The same approach,
but explicitly parameterizing the homography, have
been used in (Pritts et al., 2018a), where the authors
consider the case of conjugate translations. The case
of jointly estimating lens distortion and affine recti-
fication from coplanar features, was studied in (Pritts
et al., 2018b). All the above methods reduce the prob-
lem to a polynomial system of equation for which the
action matrix method is used (Cox et al., 2005). This
typically involves finding a Gr
¨
obner basis, and ex-
tracting template coefficients in a finite field, which
can be tedious manual work. Luckily, there are auto-
matic solvers, such as the ones presented in (Kukelova
et al., 2008a; Larsson and
˚
Astr
¨
om, 2016; Larsson
et al., 2017a; Larsson et al., 2017b; Larsson et al.,
2018b), from which the above mentioned radially dis-
torted homography solvers are derived.
An alternative to Gr
¨
obner basis methods is to
view the problem as a Quadratic Eigenvalue Prob-
lem (QEP). This was done in (Fitzgibbon, 2001) and
the same approach has been used by (Kukelova et al.,
2008b; Kayumbi and Cavallaro, 2008).
z = 1
n
z = 0
Figure 1: Illustration of the problem geometry. The ground
plane is assumed to be positioned at z = 1, and the camera
travels parallel in the plane z = 0. There are two unknown
overhead tilt angles ψ (x-axis) and θi (y-axis), which are
constant throughout the trajectory.
3 MODEL ASSUMPTIONS
We consider the original problem formulation
in (Wadenb
¨
ack and Heyden, 2013), which assumes
that a camera directed towards the floor is mounted
on a vehicle. The scale of the global coordinate sys-
tem is fixed by selecting the ground plane at z = 1, and
the camera is assumed to travel parallel to the ground,
in the plane z = 0, see Figure 1. Then, the camera
matrices for two consecutive poses A and B, are given
Radially Distorted Planar Motion Compatible Homographies
281
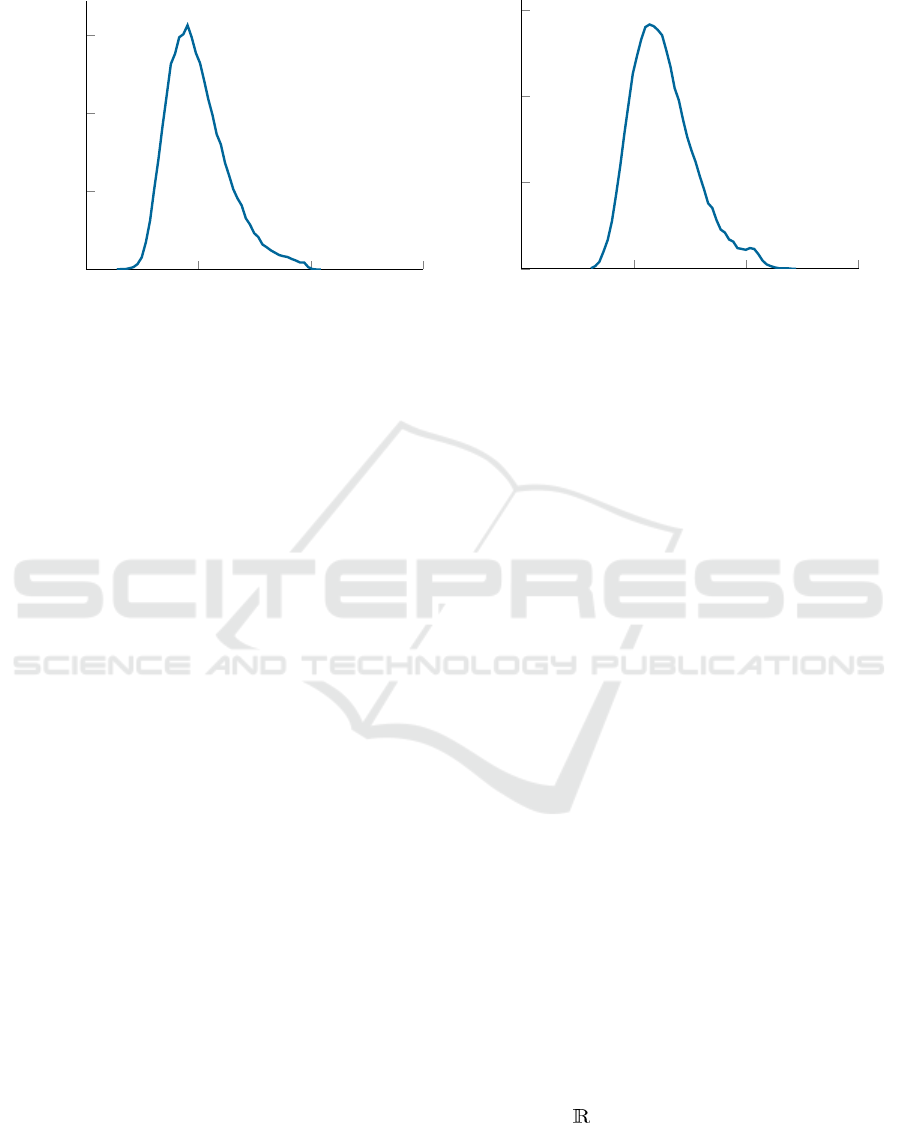
10
−20
10
−10
0
10
10
0
2
4
6
·10
−2
|λ − λ
est
|
Frequency (%)
10
−20
10
−10
0
10
10
0
2
4
6
·10
−2
kH
H
H − H
H
H
est
k
F
Frequency (%)
Figure 2: Error histogram the estimated distortion parameter λ (left) and the homography H
H
H for 100,000 random instances.
by
P
P
P
A
= R
R
R
ψθ
[I
I
I | 0
0
0],
P
P
P
B
= R
R
R
ψθ
R
R
R
φ
[I
I
I | − t
t
t],
(4)
where R
R
R
ψθ
is a rotation θ about the y-axis followed by
a rotation of ψ about the x-axis. The vehicle may ro-
tate about the z-axis by an angle φ, modeled by R
R
R
φ
,
and translate in the plane z = 0, thus leaving two
translation components t
x
and t
y
. The corresponding
homography is given by
H
H
H = λR
R
R
ψθ
R
R
R
φ
T
T
T
t
t
t
R
R
R
T
ψθ
, (5)
where T
T
T
t
t
t
= I
I
I − t
t
tn
n
n
T
is a translation matrix, for the
translation t
t
t =
t
x
t
y
0
T
, relative the plane nor-
mal n
n
n =
0 0 1
T
.
In (Wadenb
¨
ack et al., 2016) it was shown that a
planar motion compatible homography H
H
H must fulfill
11 quartic constraints. Later, it was shown that by
adding a sextic constraint, these conditions are both
necessary and sufficient (Valtonen
¨
Ornhag, 2019).
4 NON-MINIMAL RELAXATION
Note that there are six degrees of freedom in the
formulation—five in the planar motion compatible
homography and one from the distortion parameter—
hence using three points are required for the minimal
configuration. This problem is surprisingly hard, and
we have not found any tractable solution, which yields
a solver sufficiently fast and stable for real-life scenar-
ios. Instead, we propose a non-minimal relaxation,
using four point correspondences. We argue that this
compromise is acceptable, as the minimal case for a
radially distorted general homography is 4.5 points
(thus requiring 5 points in practice).
We draw inspiration from the approach
in (Kukelova et al., 2015), however, we con-
sider using only four point correspondences. By
expanding the third row of (3), one obtains
(− ˆy
i
h
11
+ ˆx
i
h
21
)x
i
+ (− ˆy
i
h
12
+ ˆx
i
h
22
)y
i
+
(− ˆy
i
h
13
+ ˆx
i
h
23
)w
i
= 0,
(6)
where w
i
= 1 + λ(x
2
i
+ y
2
i
) and ˆw
i
= 1 + λ( ˆx
2
i
+ ˆy
2
i
)
are both functions of the radial distortion parameter λ.
This is a homogeneous equation in eight monomials
v
v
v
1
=
h
11
h
12
h
13
h
21
h
22
h
23
λh
13
λh
23
T
. (7)
With four point correspondences these can be stacked
as
M
M
M
1
v
v
v
1
= 0
0
0, (8)
where M
M
M
1
is a 4× 8 matrix, and v
v
v
1
is defined as in (7).
Hence, in general, the null space of M
M
M
1
is four dimen-
sional, and we may parameterize v
v
v
1
as
v
v
v
1
=
4
∑
i=1
γ
i
n
n
n
i
, (9)
where γ
i
are the new unknowns. To fix the scale we let
γ
4
= 1. Since the elements of v
v
v
1
are not independent,
one needs to enforce two constraints, namely,
v
8
= λv
6
and v
7
= λv
3
. (10)
Next, consider the second row of (3), which can be
written
M
M
M
2
v
v
v
2
= 0
0
0, (11)
where M
M
M
2
∈
4×16
, with the null space vector v
v
v
2
con-
sisting of 7 variables, and 16 monomials: h
31
, h
32
,
h
33
, λh
33
and λ
2
γ
i
, λγ
i
, γ
i
for i = 1, 2,3 and λ
2
, λ, 1.
Since there are four equations with the same monomi-
als we can eliminate the three first variables, h
31
, h
32
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
282
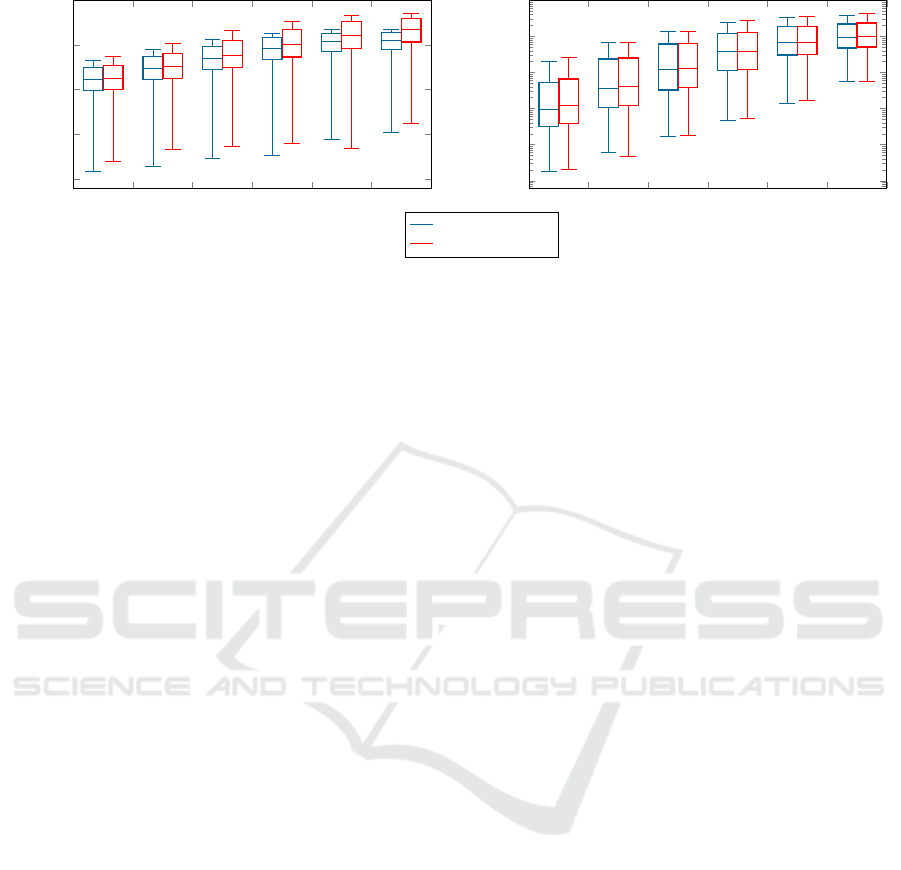
10
−3
10
−2.5
10
−2
10
−1.5
10
−1
10
−0.5
10
−7
10
−5
10
−3
10
−1
10
1
σ
|λ − λ
est
|
10
−3
10
−2.5
10
−2
10
−1.5
10
−1
10
−0.5
10
−3
10
−2
10
−1
10
0
10
1
10
2
σ
kH − H
est
k
F
Proposed (4-pt)
Fitzgibbon (5-pt)
Figure 3: Distribution of estimation error in the distortion parameter λ, and the the homography H
H
H (measured in the Frobenius
norm) for different noise levels σ. The proposed solver is compared to the five point solver (Fitzgibbon, 2001).
and h
33
, using Gauss-Jordan elimination. Performing
the elimination we obtain
ˆ
M
M
M
2
=
h
31
h
32
λh
33
h
33
λ
2
γ
1
λγ
i
γ
i
λ
2
λ 1
1 • • • ··· • • •
1 • • • · ·· • • •
1 • • • ·· · • • •
1 • • • ·· · • • •
(12)
where we notice that the columns of the right 4 × 12
submatrix are not independent. In order to generate
a correct solver, it is important to generate integer in-
stances satisfying these dependencies.
From the eliminated system
ˆ
M
M
M
2
v
v
v
2
= 0
0
0 we get the
four equations.
h
31
+ f
1
(γ
1
,γ
2
,γ
3
,λ) = 0,
h
32
+ f
2
(γ
1
,γ
2
,γ
3
,λ) = 0,
λh
33
+ f
3
(γ
1
,γ
2
,γ
3
,λ) = 0,
h
33
+ f
4
(γ
1
,γ
2
,γ
3
,λ) = 0,
(13)
where f
i
(γ
1
,γ
2
,γ
3
,λ) are polynomials in the variables
γ
1
, γ
2
, γ
3
, λ. Exploiting the relations between the last
two equations of (13), an additional constraint is ob-
tained
λ f
4
(γ
1
,γ
2
,γ
3
,λ) = f
3
(γ
1
,γ
2
,γ
3
,λ) . (14)
The eliminated variables h
31
, h
32
and h
33
are polyno-
mials of degree three, thus making (14) of degree four.
Together with (10) we have three equations in four
unknowns. Since we are able to express all elements
of the homography H
H
H as a function of four variables,
we can enforce one of the 11 quartic constraints orig-
inally found in (Wadenb
¨
ack et al., 2016). Evaluating
these constraints using H
H
H it turns out that ten of the
constraints are of degree 12 and one of degree 10 due
to cancellation of higher order terms. We choose the
smallest one to build the polynomial solver.
Using the automatic generator (Larsson and
˚
Astr
¨
om, 2016) we find that there are 18 solutions to
the problem in general, and by sampling a basis based
on the heuristic presented in (Larsson et al., 2018a) an
elimination template of size 177 × 195 could be cre-
ated.
5 EXPERIMENTS
5.1 Synthetic Data
The performance of the new polynomial solver is an-
alyzed in terms of numerical stability and noise sen-
sitivity. This is done by generating planar motion
compatible homographies and distortion parameters.
Scene points are generated and corresponding points
are mapped using the previously generated homogra-
phies, followed by radially distorting the points using
the division model.
The polynomial solver was generated according to
Section 4 in C++, and the mean run-time is 0.73 ms
(measured over 10,000 instances on a standard desk-
top computer).
5.1.1 Numerical Stability
We generate noise-free problem instances as de-
scribed in the previous section, with physically rea-
sonable parameters. As in (Kukelova et al., 2015)
the distortion parameter λ was chosen in the inter-
val [−0.7,0], which covers a wide range of distor-
tions. The error histogram for 100,000 random in-
stances are shown in Figure 2. The homographies
were normalized such that h
33
= 1. The majority
of estimated distortion parameters λ are in the error
range of 10
−10
which is acceptable for most applica-
tions; however, there are still a significant parameter
estimates of an error in the order of 10
−2
or more,
which is not negligible. This is likely to stem from
Radially Distorted Planar Motion Compatible Homographies
283

Input
Output
Figure 4: Two radially distorted images (left) and the rectified and stitched panorama. The distortion parameter and homo-
graphy was obtained using the proposed solver in a RANSAC framework. Blue border added for visualization.
the ten degree polynomial, which increases the resid-
ual error notably. Nevertheless, we show that, care-
fully incorporated in a RANSAC framework, this is
still a viable option to existing methods.
5.1.2 Noise Sensitivity
To analyze how well the solver copes with noise, the
radially distorted image coordinates were corrupted
by Gaussian noise with standard deviation σ, vary-
ing from mild to severe noise (in percent). The test
was conducted 10,000 times per noise level, see Fig-
ure 3. As a comparison we use the five point method
proposed in (Fitzgibbon, 2001). For all noise levels
the mean error for the distortion parameter λ and the
homography H
H
H, obtained using the proposed solver,
are lower compared to the five point method.
5.2 Real Images
5.2.1 Image Stitching
Stitching of images is a classic problem in computer
vision. In this section, we show that the proposed
method yields a visually acceptable output from real
data.
The images were taken using a digital camera with
a fish-eye lens mounted on a tripod, see Figure 5.
The overhead tilt was kept fixed and the entire tripod
moved along the floor, thus creating a planar motion
compatible homography between the images.
Figure 5: Setup used in the panorama stitching experiment.
We use a standard approach for estimating the
homography. First we detect and extract SURF key-
points, followed by matching them using the near-
est neighbor algorithm. Outliers are removed in a
RANSAC framework. No non-linear refinement of
the obtained homography was performed. The final
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
284

−5
0
5
·10
−7
0
50
100
150
λ
∗
λ
est
Frequency
Figure 6: (Left) Histogram of estimated distortion parameters for the proposed method evaluating during the parallel parking
sequence. The selected parameter λ
∗
is marked with a dashed line. (Middle) Undistorted image of a calibration chart, not part
of the sequence. (Right) Rectified image using the estimated parameter λ
∗
.
panorama can be seen in Figure 4. Note that the
lines appear straight in the final output, indicating that
the radial distortion parameter has been correctly es-
timated. In Figure 7 we compare the number of in-
liers vs. number of RANSAC iterations for the same
image pair, using the proposed method and the five
point solver in (Fitzgibbon, 2001). In the experiment
we mean-value the number of inliers over 500 prob-
lem instances, and the proposed method consistently
has a higher number of inliers.
Figure 7: Number of inliers vs. number of RANSAC itera-
tions for the images in Figure 4. The data has been mean-
valued over 500 test instances.
5.2.2 Application to Visual Odometry
In this final section we show that the proposed solver
can be incorporated in a VO pipeline to achieve bet-
ter performance to the compared method. The clas-
sic pipeline consists of constructing an initial solution
for the camera poses, intrinsic parameters and scene
points, and then refine these using Bundle Adjustment
(BA). In general, if a better initial solution can be ob-
tained, fewer iterations of BA are needed for the same
performance. As the latter step often amounts in a
large optimization step, it is certainly advantageous
to decrease the number of necessary iterations.
In this experiment we use the data from the mo-
bile robot experiment in (Wadenb
¨
ack et al., 2017).
The robot is equipped with omnidirectional wheels
(Fraunhofer IPA rob@work) and has a camera (with
visible radial distortion) mounted downwards, such
that the floor is predominantly in the field of view.
Reference images of a calibration pattern (checker-
board) are taken as a sanity check of the estimated
distortion parameter. Furthermore, a reference sys-
tem with an absolute accuracy of 100 µm is set up to
track the platform, from which the ground truth data
is obtained.
The robot is programmed with three sequences,
described below:
Line. Forward motion in a straight line with a con-
stant orientation (320 images),
Turn. Forward motion while rotating, resulting in a
slight turn (344 images),
Parallel Parking. Forward motion followed by a
sharp turn, while keeping constant rotation (325
images).
As in the stitching experiment in the previous sec-
tion we compare the proposed method to the one
in (Fitzgibbon, 2001). For each pair of consecu-
tive images a homography and a radial distortion pa-
rameter are estimated using both methods. Then the
method in (Wadenb
¨
ack and Heyden, 2014) is used
to recover the full set of motion parameters. From
these the trajectory of the robot is extracted and com-
pared to the ground truth, see Figure 8. Both meth-
ods perform well, with a slight preference for the pro-
posed method. This result is consistent with the find-
ings in (Valtonen
¨
Ornhag, 2019); namely, that pre-
optimization on an early stage in the VO pipeline,
does not lead to a significant performance boost. This
is, in large, due to the constraint that the constant
overhead tilt throughout the entire trajectory cannot
be enforced on a single homography alone, but rather
Radially Distorted Planar Motion Compatible Homographies
285
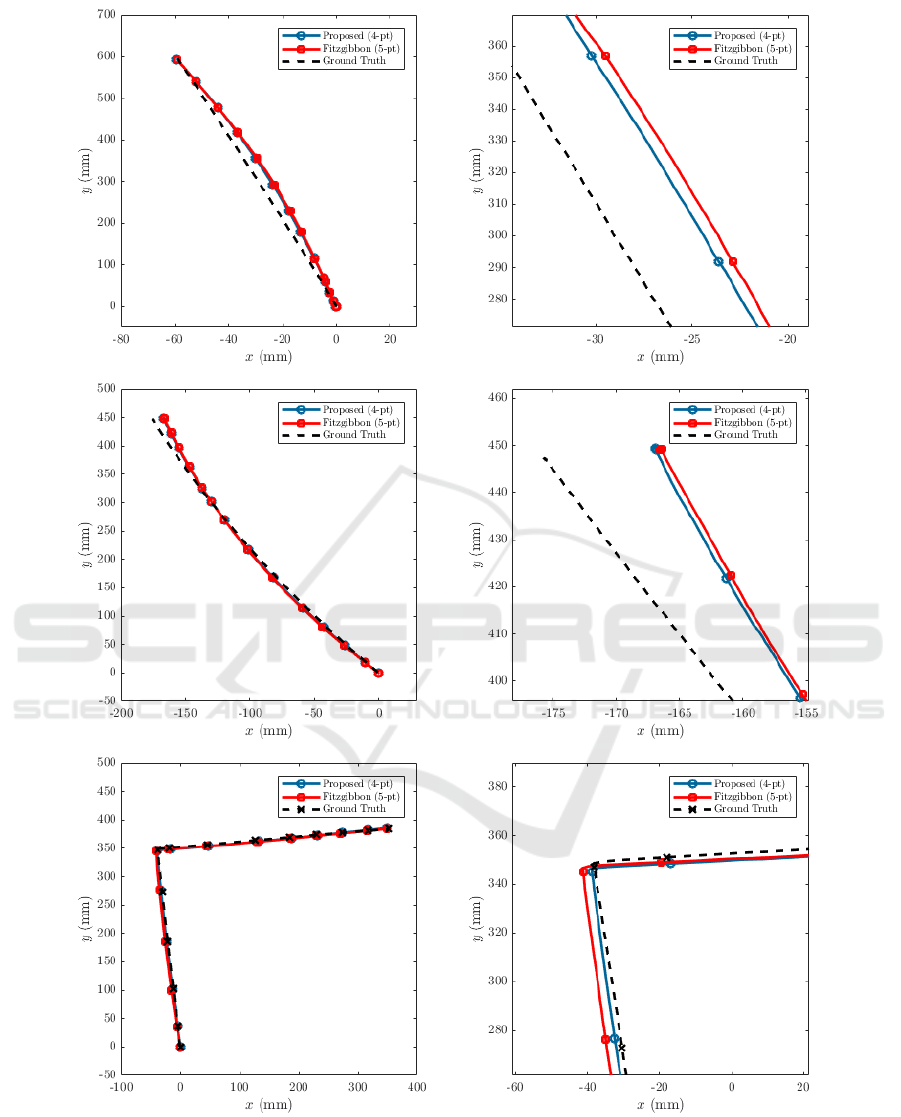
Figure 8: Estimated trajectories for line, turn and parallel parking of the VO experiment in Section 5.2.2. Images to the left
show the entire trajectory, and the ones to the right are zoomed in on a region of interest.
requires a sequence of homographies. Nevertheless,
there is still the same performance gain in terms
of the number of RANSAC iterations needed to ac-
quire a given inlier ratio, as was demonstrated in Sec-
tion 5.2.1.
The presented experiment does not enforce the
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
286

same radial distortion parameter throughout the tra-
jectory of the robot, as it estimates a new parameter
along with each homography. In order to enforce the
same radial distortion compensation, we may use his-
togram voting of the estimated distortion parameters.
In Figure 6 we have done so for the estimated para-
meters acquired during the parallel parking test se-
quence. The most likely parameter λ
∗
is then used to
rectify a previously unseen image of the calibration
scene. While the rectified image is not perfect, it may
serve as a good initial solution for further non-linear
refinement.
6 CONCLUSIONS
One cannot ignore radial distortion when estimat-
ing trajectories in a Visual Odometry framework. In
this paper we have considered radially distorted ho-
mographies compatible with the general planar mo-
tion model. We have proposed a novel algorithm
for estimating the homographies and showed on both
real and synthetic data that it increases the perfor-
mance compared to a general homography estima-
tion method with radial distortion. Furthermore, we
show, by incorporating the proposed algorithm in a
VO pipeline, that it yields satisfactory results in terms
of estimating the radial distortion parameter.
ACKNOWLEDGMENTS
The author gratefully acknowledges M
˚
arten
Wadenb
¨
ack and Martin Karlsson for providing
the data for the planar motion compatible sequences,
and Magnus Oskarsson for fruitful discussions
regarding the basis selection heuristic which made
the proposed solver faster. This work has been
funded by the Swedish Research Council through
grant no. 2015-05639 ‘Visual SLAM based on Planar
Homographies’.
REFERENCES
Brown, D. C. (1966). Decentering distortion of lenses. Pho-
togrammetric Engineering, 32:444–462.
Chen, T. and Liu, Y.-H. (2006). A robust approach for struc-
ture from planar motion by stereo image sequences.
Machine Vision and Applications (MVA), 17(3):197–
209.
Cox, D. A., Little, J., and O’Shea, D. (2005). Using Al-
gebraic Geometry. Graduate Texts in Mathematics.
Springer New York.
Fitzgibbon, A. W. (2001). Simultaneous linear estimation of
multiple view geometry and lens distortion. In Con-
ference on Computer Vision and Pattern Recognition
(CVPR).
Hajjdiab, H. and Lagani
`
ere, R. (2004). Vision-based multi-
robot simultaneous localization and mapping. In
Canadian Conference on Computer and Robot Vision
(CRV), pages 155–162, London, ON, Canada.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, Cambridge, England, UK, second edition.
Kayumbi, G. and Cavallaro, A. (2008). Multiview trajec-
tory mapping using homography with lens distortion
correction. EURASIP Journal on Image and Video
Processing, page 145715.
Kukelova, Z., Bujnak, M., and Pajdla, T. (2008a). Auto-
matic generator of minimal problem solvers. Euro-
pean Conference on Computer Vision (ECCV), pages
302–315.
Kukelova, Z., Bujnak, M., and Pajdla, T. (2008b). Polyno-
mial eigenvalue solutions to the 5-pt and 6-pt relative
pose problems. In British Machine Vision Conference
(BMVC).
Kukelova, Z., Heller, J., Bujnak, M., and Pajdla, T. (2015).
Radial distortion homography. In Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
639–647.
Larsson, V. and
˚
Astr
¨
om, K. (2016). Uncovering symme-
tries in polynomial systems. European Conference on
Computer Vision (ECCV), pages 252–267.
Larsson, V.,
˚
Astr
¨
om, K., and Oskarsson, M. (2017a). Ef-
ficient solvers for minimal problems by syzygy-based
reduction. Computer Vision and Pattern Recognition
(CVPR), pages 2383–2392.
Larsson, V.,
˚
Astr
¨
om, K., and Oskarsson, M. (2017b). Poly-
nomial solvers for saturated ideals. International
Conference on Computer Vision (ICCV), pages 2307–
2316.
Larsson, V., Kukelova, Z., and Zheng, Y. (2018a). Camera
pose estimation with unknown principal point. Com-
puter Vision and Pattern Recognition (CVPR), pages
2984–2992.
Larsson, V., Oskarsson, M.,
˚
Astr
¨
om, K., Wallis, A.,
Kukelova, Z., and Pajdla, T. (2018b). Beyond gr
¨
obner
bases: Basis selection for minimal solvers. Computer
Vision and Pattern Recognition (CVPR), pages 3945–
3954.
Liang, B. and Pears, N. (2002). Visual navigation using
planar homographies. In International Conference
on Robotics and Automation (ICRA), pages 205–210,
Washington, DC, USA.
Ort
´
ın, D. and Montiel, J. M. M. (2001). Indoor robot motion
based on monocular images. Robotica, 19(3):331–
342.
Pritts, J., Kukelova, Z., Larsson, V., and Chum, O. (2018a).
Radially-distorted conjugate translations. In Confer-
ence on Computer Vision and Pattern Recognition
(CVPR).
Pritts, J., Kukelova, Z., Larsson, V., and Chum, O. (2018b).
Radially Distorted Planar Motion Compatible Homographies
287

Rectification from radially-distorted scales. In Asian
Conference of Computer Vision (ACCV), pages 36–52.
Valtonen
¨
Ornhag, M. (2019). Fast non-minimal solvers for
planar motion compatible homographies. In Inter-
national Conference on Pattern Recognition Applica-
tions and Methods (ICPRAM), pages 40–51, Prague,
Czech Republic.
Wadenb
¨
ack, M. and Heyden, A. (2013). Planar motion and
hand-eye calibration using inter-image homographies
from a planar scene. International Conference on
Computer Vision Theory and Applications (VISAPP),
pages 164–168.
Wadenb
¨
ack, M. and Heyden, A. (2014). Ego-motion recov-
ery and robust tilt estimation for planar motion using
several homographies. International Conference on
Computer Vision Theory and Applications (VISAPP),
pages 635–639.
Wadenb
¨
ack, M., Karlsson, M., Heyden, A., Robertsson, A.,
and Johansson, R. (2017). Visual odometry from two
point correspondences and initial automatic tilt cali-
bration. In International Joint Conference on Com-
puter Vision, Imaging and Computer Graphics Theory
and Applications (VISIGRAPP 2017), pages 340–346.
Wadenb
¨
ack, M.,
˚
Astr
¨
om, K., and Heyden, A. (2016). Re-
covering planar motion from homographies obtained
using a 2.5-point solver for a polynomial system. In-
ternational Conference on Image Processing (ICIP),
pages 2966–2970.
Zienkiewicz, J. and Davison, A. J. (2015). Extrinsics auto-
calibration for dense planar visual odometry. Journal
of Field Robotics (JFR), 32(5):803–825.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
288
