Optimization of Coupling Efficiency of Fiber Optic Rotary

Joint by Ray Tracing

Chun-Han Chou

, Rou-Jhen Chen, Hsin-Yi Tsai

, Kuo-Cheng Huang and Chih-Chung Yang

National Applied Research Laboratories, Taiwan Instrument Research Institute, 20 R&D Rd. VI, Hsinchu Science Park,

Hsinchu City 30076, Taiwan

Keywords: Fiber Optic Rotary Joint, Coupling, Manufacture Error, Dove Prism, Tolerance Analysis.

Abstract: In the paper, a misalignment and field magnification tolerance analysis for the coupling efficiency of fiber

optic rotary joint was presented. The analysis consisted of output position deviations from different

wavelengths, dove prism manufacturing errors, light tilt and decenter errors. It helped manufacturers easily

defined component specifications and assembly tolerances for fiber optic rotary joint. The 2 mm spot size was

best suited for current assembly tolerances. The 2 mm beam diameter of coupling efficiency was over 80% in

the tilt error ±10 arcmin and decenter error ±250 μm. In the future, we could create a FORJ system according

to the simulation parameters. The practice experiment data would compare to our simulation results that used

to prove our simulation results.

1 INTRODUCTION

Currently, the automation industry was growing

rapidly. It required a large number of signal

transmission components to connect each part of the

component. The fiber optic rotary joint(FORJ) was

used to transmit signals across rotary interface (Jia,

Jing, Zhang, Wang, Tang and Zhang, 2005). FORJ was

widely used in the lot of fields of remotely operated

vehicles, oceanographic winches, cable reels, towed

arrays, dipping sonar, undersea telemetry and Robotics

etc. The traditional multi-pass of FORJ required high

precision alignment to reduce signal coupling losses

(Liu, Zhu, Jiang and Gao, 2013). Due to manufacturing

difficulties, people began to look for another way to

solve the problem. People began to use the different

ways of C-lens (Jia, Jing, Zhang, Zhou, Zhang and

Tang, 2005) and GRIN lens (Shi, Klafter and Harstead,

1985). Even these methods could reduce the coupling

loss, but it was difficult to continuously transmit multi-

signals when the interface continue rotation. Another

group of People used other ways of multi-reflector

mirror (Liu and Chen, 2006), diffractive element

(Mathias and Sverker, 1999) and symmetrical optical

system (DENG, ZHOU and LIU, 2001) etc. These

methods could overcome the problem of multiple

https://orcid.org/0000-0003-2460-5875

https://orcid.org/0000-0001-8275-6132

signal transmission, but these systems had the

disadvantages of large system size and high cost etc.

Previously problems were solved until people used

dove prism for FORJ. The structure of FROJ composed

of fiber array, collimator lens and dove prism. The

system was smaller than the multi-mirror and

symmetrical optics, and it continued to transmit

multiple signals as the interface continued to rotate

(Jia, Yu, Jing, Zhang, and Zhang, 2008). The key factor

of the dove prism type of FORJ was the manufacture

error of dove prism and the assemble tolerance of the

system (Shapar, 2018). Enoch group used exact ray

trace to calculate the interferometric Dove prism

tolerance to manufacturing errors, but they didn’t

mention the prism alignment tolerance (Gutierrez-

Herrera and Strojnik, 2008).

Therefore, we presented a misalignment and field

magnification tolerance analysis for the FORJ

coupling efficiency. It helped producers easily defined

element specifications and assembly tolerances for

FORJ. The tolerance analysis had the output position

deviation of different wavelength, light source position

error, dove prism manufacture error, light source tilt

and decenter error. Tolerance analysis showed the

complete relationship between coupling efficiency and

manufacturing and assembly errors.

Chou, C., Chen, R., Tsai, H., Huang, K. and Yang, C.

Optimization of Coupling Efﬁciency of Fiber Optic Rotary Joint by Ray Tracing.

DOI: 10.5220/0008895200710075

In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 71-75

ISBN: 978-989-758-401-5; ISSN: 2184-4364

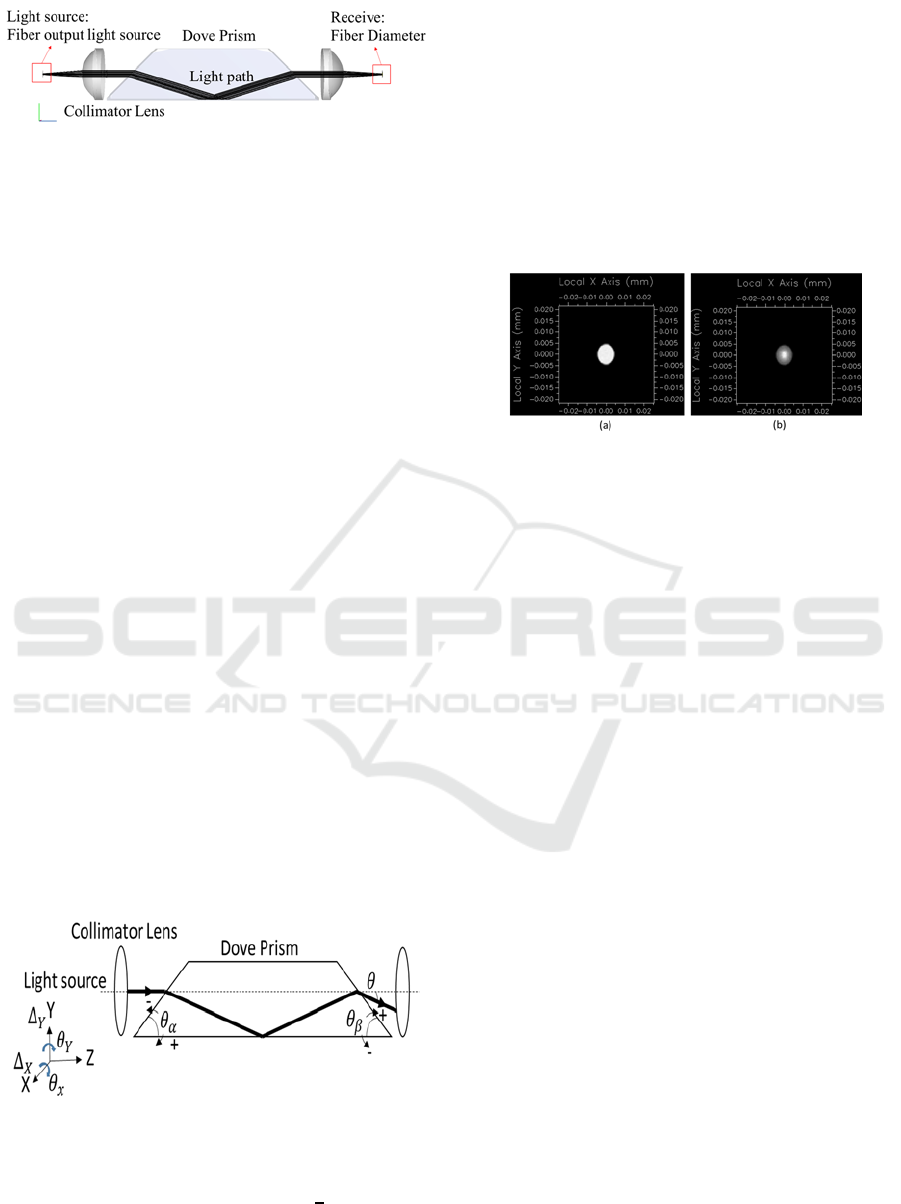
Figure 1: FORJ simulation model.

In the section 2, the FORJ simulation parameters

and light propagation mathematical formula were

introduced. In the section 3, the tolerance analysis

results were introduced. In the section 4, the

simulation results are discussed. In the section 5, the

conclusion was introduced.

2 FORJ MODEL

CONSTRUCTION

The FORJ tolerance analysis composed of output

position deviation of different wavelength, light

source position error, dove prism manufacture error,

light source tilt and decenter error. The tolerance

analysis was created by the optical simulation

software (FRED). The software simulated the

propagation of light through FORJ by raytracing. The

FORJ composed of fiber, collimation lens and dove

prism, as shown in Figure 1.

The light output through the collimating lens was

approximately parallel to the optical axis of the dove

prism. In the ideal dove model, the direction of light

propagation after the dove was the same as the input

light. In practice, the dove prism had manufacturing

errors, so the direction of the output light was different

from the direction of the input light, as shown in Figure

2. In the paper, the size of dove prism was 25 x 25 x

105.68 



with the size tolerance of 0.13 Legs,

0.38 Hypotenuse. The angular tolerance of the dove

prism input and output interface was 2 armin [13].

Figure 2: Ray propagation in the dove prism.

The ray propagation output deviation formula:

θ



cos











sin









cos 





(1)

Where 



is the input surface of dove prism, 



is the

exit surface of dove prism, n is the dove prism

reflection index.

In the optical simulation software, we built a

complete FORJ model. These simulated parameters

were collected from the actual optical components.

Through different dove prism manufacturing errors

and assembly errors, we could obtain different

efficiency, spot size and spot position on the receiver,

as shown in Figure 3. These data could use to create

the tolerance analysis.

Figure 3: Simulation irradiance map. (a) Fiber output light

source. (b) Through the FROJ output light source.

3 THE FORJ TOLERANCE

ANALYSIS

3.1 Output Spot Position of Different

Wavelength

The wavelengths commonly used for fiber-optic

communication signals were 850 nm, 1310 nm, and

1550 nm. The different wavelength had the different

reflection index in the same material. Therefore,

different wavelengths of light passing through the dove

prism had different spot positions, as shown in Figure

4. The short wavelengths had a higher reflectance

index in dove prism materials, so the positional

deviation was larger. The positional deviation between

850 nm and 1550 nm was approximately 400 μm.

Therefore, the position of receiver of FORJ could tune

from 0 to 400 μm, it could accommodate the three

different communication wavelengths.

3.2 Fiber Couple Tolerance Analysis

The FORJ coupling error consisted of dow prism

manufacturing errors, source tilt and decenter errors.

The light source generated beams of different

diameters through the collimating lens. The beams of

different diameters affected the FORJ tolerance

distribution. In this section, we used different

diameter beams to perform tolerance analysis in

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

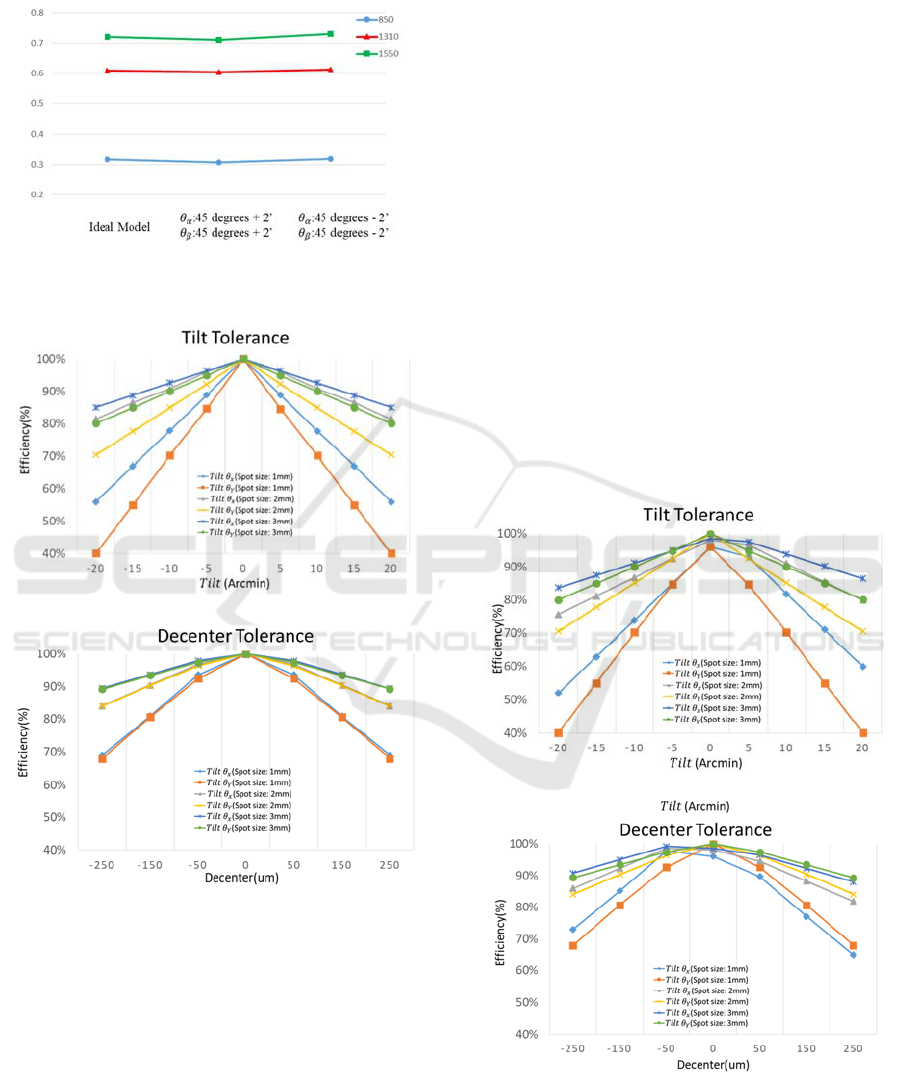
different dove prism manufacturing errors, as shown

in Figure 5, 6 & 7.

Figure 4: The different manufactory errors of FORJ of

output spot position deviation with different wavelength.

(a)

(b)

Figure 5: Different diameter beams tolerance analysis in the

ideal dove Prism. (a) Input light tilt tolerance analysis. (b)

Input light decenter tolerance analysis.

According to the tolerance simulation results, the

tolerance distribution of the small diameter beam was

more sensitive than the large diameter beam. When

the diameter of beam was 1mm and the light of tilt Y

tolerance was ±20 arcmin, the coupling efficiency

dropped to 40%. When the diameter of beam was

3mm and the light of tilt Y tolerance was ±20 arcmin,

the coupling efficiency was still over 80%. When the

decenter was within ±250 μm, the beam coupling

efficiency over 2 mm diameter exceeded 80%. In the

manufacturing error of different dove prisms, the

tolerance distribution changed, and the efficiency

difference was about 5%.

4 DISCUSSION

The spot positional deviation between 850 nm and

1550 nm was approximately 400 μm. The key factor

affecting the assembly tolerance distribution was the

beam diameter. The tolerance distribution of the tilt

Y felled faster than the tilt X. When the diameter of

beam was 1mm and the light of tilt Y tolerance was

±20 arcmin, the coupling efficiency dropped to 40%.

When the diameter of beam was 3 mm and the light

of tilt Y tolerance was ±20 arcmin, the coupling

efficiency was still over 80%. When the decenter was

within ±250 μm, the beam coupling efficiency over 2

mm diameter exceeded 80%. Therefore, in the

assembly tolerance, the tilt tolerance was more

sensitive than the decenter tolerance.

(a)

(b)

Figure 6: Different diameter beams tolerance analysis in the

manufacture error dove Prism. (:45 degrees - 2’,

:45

degrees - 2’) (a) Input light tilt tolerance analysis. (b) Input

light decenter tolerance analysis.

Optimization of Coupling Efﬁciency of Fiber Optic Rotary Joint by Ray Tracing

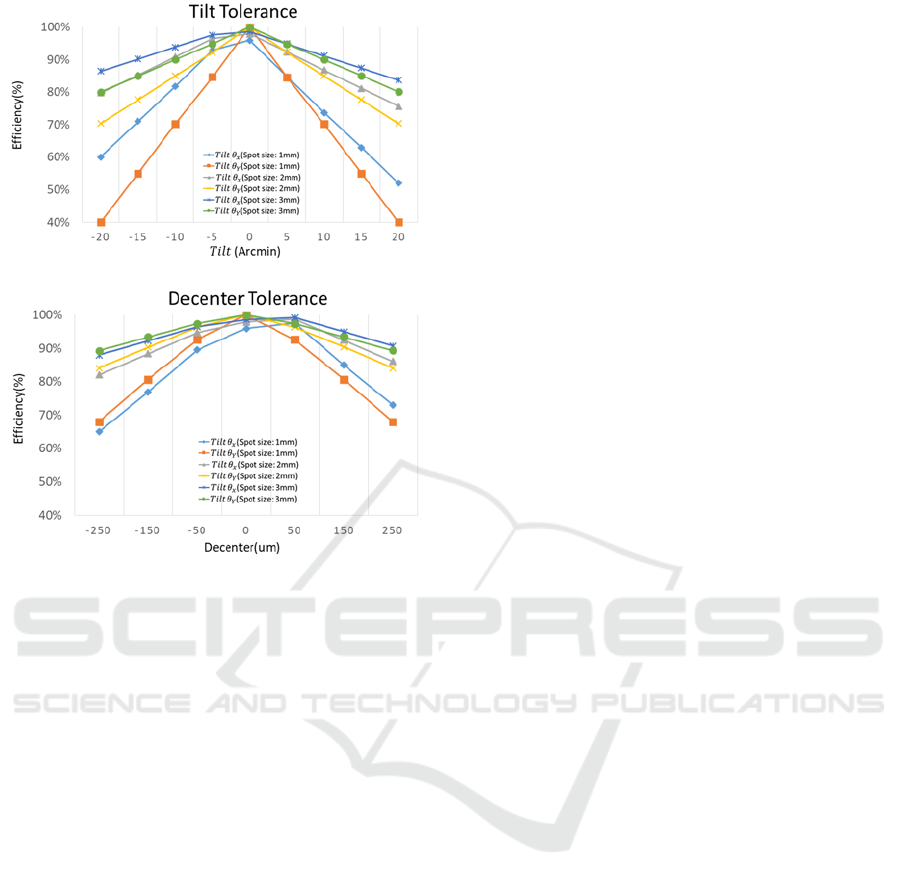
(a)

(b)

Figure 7: Different diameter beams tolerance analysis in the

manufacture error dove Prism. (



:45 degrees + 2’, 



:45

degrees + 2’) (a) Input light tilt tolerance analysis. (b) Input

light decenter tolerance analysis.

At present, the optical component tilt error was

less than ±10 arc minutes, and the decenter error was

less than ±50 μm. Therefore, in the current assembly

tolerances, the suitable beam diameter was 2 mm. The

2 mm beam diameter of coupling efficiency was over

80% in the tilt error ±10 arcmin and decenter error

±250 μm. The 2 mm cross-sectional area was 44%

smaller than the 3 mm cross-sectional area. The FORJ

could arrange more fibers and transmit more signals

at the same time. If the FORJ want to accommodate

three different communication wavelengths, he

position of receiver of FORJ required tuning range

from 0 to 400 μm.

5 CONCLUSIONS

In the paper, a misalignment and field magnification

tolerance analysis for the coupling efficiency of FORJ

was presented. It helped producers easily define

element specifications and assembly tolerances for

FORJ. The 2 mm beam diameter was the most

suitable for current assembly tolerances. The

coupling efficiency exceeded 80% when the tilt error

was ±10 arcmin and the decenter error was ±250 μm.

If the FORJ want to accommodate three different

communication wavelengths, the position of receiver

of FORJ required tuning range from 0 to 400 μm. In

the future, we could create a FORJ system according

to the simulation parameters. The practice experiment

data would compare to our simulation results that

used to prove our simulation results.

ACKNOWLEDGEMENTS

The authors would like to express their appreciation

for financial aid from the Ministry of Science and

Technology, R.O.C under grant numbers MOST 108-

2221-E-492-019, MOST 108-2218-E-492-010 and

MOST 107-2622-E-492-017-CC3. The authors

would also like to express their gratitude to the

Taiwan Instrument Research Institute of National

Applied Research Laboratories for the support.

REFERENCES

Jia, D., Jing, W., Zhang, Y., Wang, G., Tang, F., & Zhang,

J. (2005). Bidirectional dynamic data transmission

through a rotary interface. Optical Engineering, 44(5),

050503.

Liu, J., Zhu, B., Jiang, H., & Gao, W. (2013). Image

analysis measurement of cottonseed coat fragments in

100% cotton woven fabric. Fibers and Polymers, 14(7),

1208-1214.

Jia, D. G., Jing, W. C., Zhang, Y. M., Zhou, G., Zhang, J.,

& Tang, F. (2005). Low-loss fiber optic rotary joint

using C-lens collimators. Optoelectronics Letters, 1(3),

221.

Shi, Y., Klafter, L., & Harstead, E. (1985). A dual-fiber

optical rotary joint. Journal of lightwave technology,

3(5), 999-1004.

Liu, L., & Chen, N. G. (2006). Double-pass rotary mirror

array for fast scanning optical delay line. Applied

optics, 45(21), 5426-5431.

Mathias Johansson, Sverker Hard. (1999). Design,

fabrication, and evaluation of a multi-channel

diffractive optic rotary joint,Applied Optics, 38(8):

1302-1310

Deng, Y. X., Zhou, G., & Liu, W. (2001). Dual-channel

fiber optic rotary joint of symmetrical optical system,

Journal of Optoelectronics·Laser, 12（8）：792-794

Jia, D., Yu, C., Jing, W., Zhang, H., & Zhang, Y. (2008,

January). Effect of misalignment on rotating coupling

efficiency of the Dove prism. In Advanced Materials

and Devices for Sensing and Imaging III (Vol. 6829, p.

68290S). International Society for Optics and

Photonics.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

Shapar, V. (2018). Principles of compensation of optical

rays’ rotation and multi-channel optical rotary

connectors. Applied optics, 57(27), 8023-8033.

Gutierrez-Herrera, E., & Strojnik, M. (2008).

Interferometric tolerance determination for a Dove

prism using exact ray trace. Optics Communications,

281(5), 897-905.

Optimization of Coupling Efﬁciency of Fiber Optic Rotary Joint by Ray Tracing