Optical Frequency Comb Generated with an Amplitude Modulated

Pump in Silicon Nitride Ring-resonators

Jose M. Chavez Boggio

, Daniel Bodenm

uller

, S. A. Ahmed

1,2

, Adnan M. Baig

1,2

and Martin M. Roth

innoFSPEC-VKS, Leibniz Institute f

ur Astrophysik Potsdam (AIP), An der Sternwarte 16, D-14482 Potsdam, Germany

Institut f

ur Physik und Astronomie, Potsdam Universit

at, Potsdam, Germany

Keywords:

Optical Frequency Combs, Silicon Nitride Ring-resonator, Soliton.

Abstract:

The coherence of the repetition-rate of optical frequency combs when generated using an amplitude modu-

lated pump is experimentally investigated. We show that the repetition-rate of the frequency comb exhibit

a linewidth of ∼ 25 Hz even when the mismatch between the modulation frequency and the resonator free-

spectral range is larger than the linewidth of the resonances of the ring-resonator.

1 INTRODUCTION

State-of-the-art complementary metal-oxide semi-

conductor (CMOS) technology allows the precise

fabrication of photonic circuits with nanometer-level

accuracy, potentially enabling the merging of elec-

tronic and photonic components on a chip. CMOS-

compatible materials have received increased atten-

tion in the last few years for nonlinear on-chip de-

vices (Foster et al., 2006) (Jalali, 2007) (Leuthold

et al., 2010) (Zajnulina et al., 2014) (Chavez Boggio

et al., 2014a) (Chavez Boggio et al., 2016) (Cohen

et al., 2018) (Xue et al., 2019). Optical frequency

combs (OFCs) generated in high quality-factor (Q)

silicon nitride (Si

) ring-resonators is an example

of such a miniature device. By pumping the ring-

resonator with a continuous-wave (CW) laser, it has

been demonstrated the generation of frequency combs

with octave spanning bandwidths (Okawachi et al.,

2011) (Papp et al., 2013) (Wang et al., 2017) (Hendry

et al., 2019). However, fully coherent OFCs require

the formation of solitons which are obtained through

a complex pump wavelength tuning with very pre-

cise scanning speed and range. Furthermore, small

changes in the intra-cavity power lead to temperature

changes and therefore to changes of the free-spectral

range (FSR) of the resonator. In (Del’Haye et al.,

2012), it was shown that 1 mW of power ﬂuctuation

can lead to a change of 6 kHz in the FSR. This im-

pose that an active stabilization mechanism has to be

implemented in order to generate OFCs with stable

repetition-rates.

Recently, it has been proposed that by injecting

a modulated pump in the ring resonator with a fre-

quency matching its FSR, the threshold for frequency

comb generation is much lower than by using a CW

pump. Furthermore, the pump to frequency comb

conversion efﬁciency is much higher than for the CW

case (Obrzud et al., 2017). It was also shown that the

stability of the modulation signal is transferred to the

repetition-rate of the OFC, opening the possibility of

ultra-stable devices. The OFC repetition-rate stability

is a critical characteristic not only for spectroscopic or

metrological applications but also for the calibration

of astronomical spectrographs (Chavez Boggio et al.,

2014b) (Zajnulina et al., 2015) (Chavez Boggio et al.,

2018). It was experimentally shown that by varying

the driving external modulation frequency, the soli-

ton pulse repetition-rate could adiabatically follow

the external frequency up to a frequency mismatch

of 60 kHz and then the soliton (frequency comb) is

annihilated (Obrzud et al., 2017). The authors cal-

culate the change of the FSR of the resonator corre-

sponding to the heating effect when the laser wave-

length matches the resonance. This change is only

a few kHz, which is much smaller than the reported

mismatch tolerance. Even though this makes a tight

compromise and reduce the practicality of such ap-

proach. In this paper we experimentally demonstrate

that the external modulation can have a mismatch in

excess of several hundred of MHz with respect to the

FSR (larger than the linewidth of the resonances in

our resonator) and still produce stable OFCs.

Section 2 describes our experimental arrangement

Boggio, J., Bodenmüller, D., Ahmed, S., Baig, A. and Roth, M.

Optical Frequency Comb Generated with an Amplitude Modulated Pump in Silicon Nitride Ring-resonators.

DOI: 10.5220/0008896400170021

In Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2020), pages 17-21

ISBN: 978-989-758-401-5; ISSN: 2184-4364

and procedure, while section 3 describes the experi-

mental results. Finally in section 4 we draw our con-

clusions.

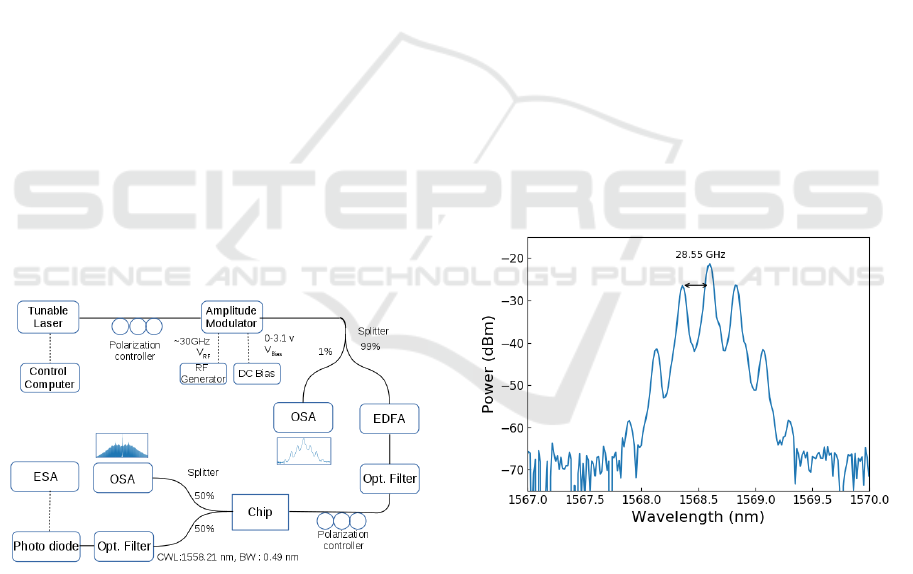
2 EXPERIMENTAL SETUP

A tunable laser centered at λ

= 1568.7 nm and pro-

viding 12 mW continuous wave (CW) power serves

as the pump. The pump light is amplitude modulated

using a LiNbO

modulator. A signal generator drives

the modulator with a frequency nearly matching the

spacing between the resonances in our ring-resonator.

With a bias voltage, the shape of the modulation is ad-

justed to maximize the optical frequency comb band-

width. The modulated light is splitted with a 1/99

splitter and its spectrum is monitored through the 1%

port using an optical spectrum analyser (OSA). The

99% port is directed into an Erbium-doped ﬁber am-

plifer (EDFA) where the pump is ampliﬁed to a nomi-

nal power of 3.5 W. The ampliﬁed light is then propa-

gated through a band-pass optical ﬁlter in order to ﬁl-

ter out the ampliﬁed spontaneous emission noise from

the EDFA. With a polarization controller, the polar-

ization of the pump is adjusted in order to match the

quasi-TE mode of the ring-resonator. The pump light

is injected into the chip by either using a ﬁber lens

or an objective lens (having NA 0.85). The silicon ni-

tride ring-resonator has a radius of ∼ 800 µm resulting

in resonances spaced by 28.55 GHz.

Figure 1: Experiment setup for frequency comb generation.

The measured Q-factor of the resonator is ∼ 2 ×

, corresponding to a resonance linewidth of ∼

100 MHz. The ring-resonator transversal dimensions

are: width = 1.7 µm and height = 800 nm. The chip

contains inverse tapered bus-waveguides to in- and

out-coupling the light. The nominal losses are 2 dB

for each end. The gap between the bus waveguide

and the ring is 550 nm which corresponds nearly to

critically coupling the light into the resonator. The

pump power coupled into the chip is estimated to be

400 mW. The generated frequency comb light is out-

coupled from the chip using a lensed ﬁber and then

splitted in 50/50. One part is directed to a band-pass

optical ﬁlter (center λ = 1558.21 nm and bandwidth =

0.49 nm). This allows to ﬁlter out two comb lines of

the generated OFC. The beat note of the comb lines

is detected with a high-speed photodiode and visu-

alized with an electrical signal analyser (ESA). The

other splitter arm is connected to an OSA (0.05 nm

resolution bandwidth) for the visualization of the fre-

quency comb spectrum.

3 EXPERIMENTAL RESULTS

The spectrum of the pump laser after the amplitude

modulation is performed is shown in ﬁg. 2. In the

time domain this corresponds to a pulse train having

a repetition-rate of 28.55 GHz. The more contiguous

sidebands to the central pump are only 5 dB lower

in power, indicating a strong modulation. The pulse

width of this pulse train is estimated to be 25 ps. The

dissipative Kerr solitons (DKS) formation in the ring-

resonator is expected to be locked to the repetition-

rate of this initial pulse train and the generated soliton

will sit on top of the initial pulses.

Figure 2: Spectrum of the amplitude modulated pump.

Fig. 3 shows the frequency comb spectrum when

the amplitude modulation was set to 28.55 GHz,

which corresponds to the resonator FSR. The OFC

exhibits a ±15 dB bandwidth of 100 nm. Over this

bandwidth the OFC has 430 comb lines. It is esti-

mated that the pump to comb lines conversion efﬁ-

ciency is 10%, which is much larger than when the

OFC is generated using a CW pump. The inset shows

a zoom of the generated frequency comb in the region

1550 - 1560 nm. The smooth spectral envelop shape

approaches a sech

- shape, which is typical of DKS.

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

Contrary to CW pumped resonators, where reliable

generation of DKS is challenging, by using a modu-

lated pump it is straight forward.

Figure 3: Frequency comb spectrum obtained when the am-

plitude modulation frequency is set at f = 28.55 GHz.

By optically ﬁltering two frequency comb lines

around 1558 nm, we could measure their beat note

using a fast photodiode and assess the noise charac-

teristics of the repetition-rate of the OFC. The ESA

resolution was set at 2 kHz. Fig. 4 shows the spec-

trum of the repetition-rate signal over a 100 MHz

bandwidth and centered at the modulation frequency

(28.55 GHz). There is negligible noise build-up for

the spectral components different than the modula-

tion frequency (28.55 GHz), indicating that the DKS

perfectly acquires the external modulation frequency

while other spectral components are completely neg-

ligible.

Figure 4: Beat note of the frequency comb repetition-rate.

Fig. 5 shows the frequency comb spectrum ob-

tained when the modulation frequency was set at

28.68 GHz. This is 80 MHz larger than the FSR of

the resonator and larger than the linewidth of the res-

onance (100 MHz). Note that the spectrum is less

round than in Fig. 3, but has a bump of intensity at

1560 and 1580 nm. This is an indication that not only

a fundamental soliton is being generated but a higher-

order soliton (with low power) also propagates in the

ring-resonator.

Figure 5: Frequency comb spectrum obtained when the am-

plitude modulation frequency is set at f = 28.68 GHz.

The repetition-rate of the frequency comb ob-

tained with a resolution bandwidth of the ESA set at

20 Hz is shown in ﬁg. 6. The linewidth of the fre-

quency comb repetition-rate is comparable to the res-

olution bandwidth of the electrical spectrum analyzer

(20 Hz). In (Obrzud et al., 2017), it was reported that

the mismatch between the modulation frequency and

the repetition-rate of the resonator could not be more

than 60 kHz before the frequency comb collapses. In

our experiment, we could continuously tune the mod-

ulation frequency by tens of MHz and the frequency

comb adapts adiabetically and does not collapse dur-

ing the tuning process.

Figure 6: Repetition-rate of the frequency comb with a

pump modulated at 28.68 GHz.

Optical Frequency Comb Generated with an Amplitude Modulated Pump in Silicon Nitride Ring-resonators

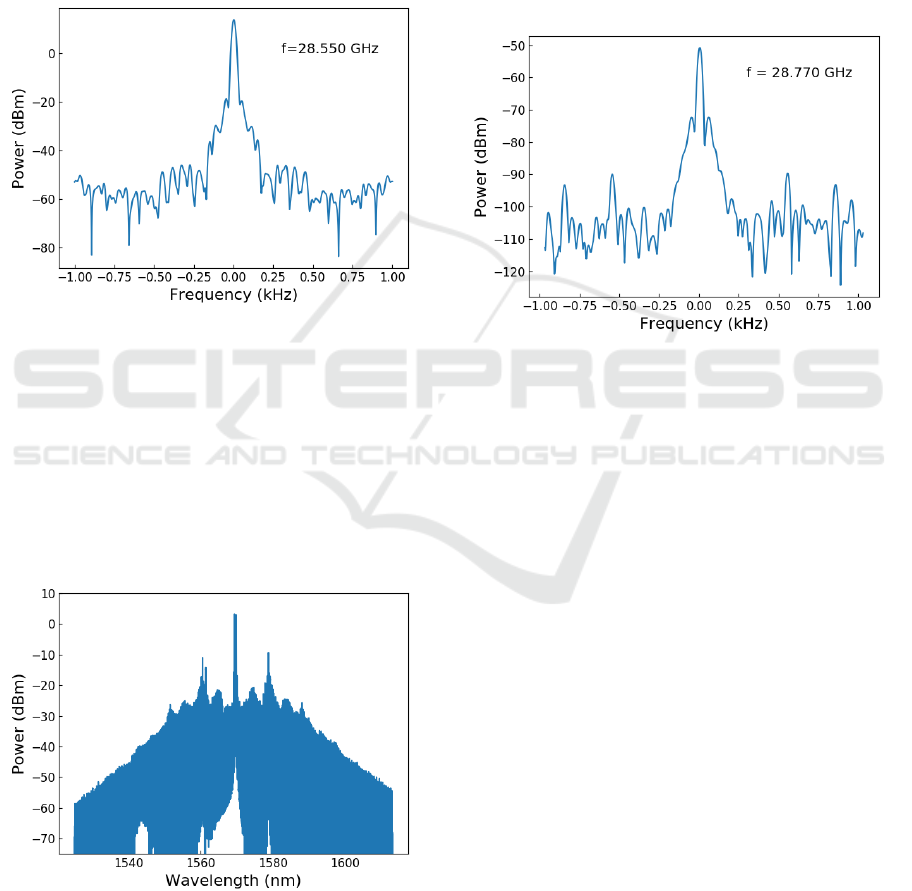
Fig. 7 shows the spectrum of the electrical sig-

nal driving the amplitude modulator taken with the

ESA with a resolution bandwidth set at 20 Hz. This

shows that as the frequency comb is generated it

builds up from the exact external modulation fre-

quency. The OFC repetition-rate linewidth exhibits

negligible broadening if compared to the modulating

signal, even though hundreds of comb lines are gener-

ated in a complex cascaded four-wave-mixing process

(Sodre Jr et al., 2008).

Figure 7: Spectrum of the electrical signal driving the am-

plitude modulator.

Fig. 8 shows the OFC generated when the mod-

ulation frequency is set to 28.77 GHz. Note that the

spectrum is even more structured than the one in ﬁg. 5.

This indicates that as the modulation frequency shifts

from the resonator FSR frequency, it is more difﬁcult

to generate a temporal fundamental soliton but there

is also a high-order soliton co-propagating with the

fundamental soliton.

Figure 8: Frequency comb spectrum at f = 28.77 GHz.

Fig. 9 shows the repetition-rate of the frequency

comb. Even though it exhibits a narrow linewidth,

sidebands grow considereably if compared to Fig. 7.

As the modulation frequency de-synchronizes further

from the FSR of the resonator, the repetition-rate of

the frequency comb becomes weaker in power and

noisy and eventually a DKS can not be any longer

generated. The largest de-synchronization for what

we could still have a frequency comb repetition-rate,

locked to the external modulation frequency, was ∼

600 MHz. For that mismatch, the repetition-rate sig-

nal was very weak and noisy. For larger mismatches,

the frequency comb could not operate locked at the

external modulation frequency.

Figure 9: Repetition-rate of the frequency comb generated

with a pump modulated at 28.77 GHz.

In (Obrzud et al., 2017) it was shown that the soli-

ton central wavelength shifts as a consequence of the

mismatch between the external modulating frequency

and the FSR of the resonator. The experimental cen-

tral wavelength shift was found to be 120 GHz for

30 kHz mismatch. With our parameters of 220 MHz

shift, that would correspond to 840 THz. However

from the spectra in Fig. 2, 5 and 8 no noticeable cen-

tral wavelength shift can be observed.

4 CONCLUSIONS

Frequency comb generation using an amplitude mod-

ulated pump has been experimentally investigated.

The modulation frequency was detuned from the free-

spectral range of the resonator by several hundred of

MHz in order to assess the robustness of the gener-

ated solitons under external modulation. Optical fre-

quency combs with 100 nm bandwidth and repetition-

rate of 28.55 GHz were generated. It was shown that

the soliton is adiabatically locked to the external mod-

ulation frequency, even though the large mismatch

with the FSR of the resonator. The linewidth of the

repetition-rate of the OFC exhibit negligible broad-

ening if compared with the linewidth of the modu-

PHOTOPTICS 2020 - 8th International Conference on Photonics, Optics and Laser Technology

lating signal. Our ﬁndings should open new avenues

towards OFCs with ultra-stable repetition-rates.

ACKNOWLEDGEMENTS

This work was supported by BMBF (Federal Min-

istry of Education and Research) through grants

03Z2AN11 and 03Z2AN12.

REFERENCES

Chavez Boggio, J., Bodenm

uller, D., Fremberg, T., Haynes,

R., Roth, M. M., Eisermann, R., Lisker, M., Zimmer-

mann, L., and B

ohm, M. (2014a). Dispersion engi-

neered silicon nitride waveguides by geometrical and

refractive-index optimization. JOSA B, 31(11):2846–

2857.

Chavez Boggio, J., Fremberg, T., Bodenm

uller, D., Sandin,

C., Zajnulina, M., Kelz, A., Giannone, D., Rutowska,

M., Moralejo, B., Roth, M., et al. (2018). Wavelength

calibration with pmas at 3.5 m calar alto telescope us-

ing a tunable astro-comb. Optics Communications,

415:186–193.

Chavez Boggio, J., Fremberg, T., Moralejo, B., Rutowska,

M., Hernandez, E., Zajnulina, M., Kelz, A., Bo-

denm

uller, D., Sandin, C., Wysmolek, M., et al.

(2014b). Astronomical optical frequency comb gen-

eration and test in a ﬁber-fed muse spectrograph. In

Advances in Optical and Mechanical Technologies for

Telescopes and Instrumentation, volume 9151, page

915120. International Society for Optics and Photon-

ics.

Chavez Boggio, J., Mo

nux, A. O., Modotto, D., Frem-

berg, T., Bodenm

uller, D., Giannone, D., Roth,

M., Hansson, T., Wabnitz, S., Silvestre, E., et al.

(2016). Dispersion-optimized multicladding silicon

nitride waveguides for nonlinear frequency gener-

ation from ultraviolet to mid-infrared. JOSA B,

33(11):2402–2413.

Cohen, R. A., Amrani, O., and Ruschin, S. (2018). Re-

sponse shaping with a silicon ring resonator via dou-

ble injection. Nature Photonics, 12(11):706.

Del’Haye, P., Papp, S. B., and Diddams, S. A. (2012). Hy-

brid electro-optically modulated microcombs. Physi-

cal Review Letters, 109(26):263901.

Foster, M. A., Turner, A. C., Sharping, J. E., Schmidt, B. S.,

Lipson, M., and Gaeta, A. L. (2006). Broad-band opti-

cal parametric gain on a silicon photonic chip. Nature,

441(7096):960.

Hendry, I., Garbin, B., Murdoch, S. G., Coen, S., and

Erkintalo, M. (2019). Impact of de-synchronization

and drift on soliton-based kerr frequency combs in

the presence of pulsed driving ﬁelds. arXiv preprint

arXiv:1905.09810.

Jalali, B. (2007). Teaching silicon new tricks. In

OFC/NFOEC 2007-2007 Conference on Optical

Fiber Communication and the National Fiber Optic

Engineers Conference, pages 1–23. IEEE.

Leuthold, J., Koos, C., and Freude, W. (2010). Nonlinear

silicon photonics. Nature photonics, 4(8):535.

Obrzud, E., Lecomte, S., and Herr, T. (2017). Temporal

solitons in microresonators driven by optical pulses.

Nature Photonics, 11(9):600.

Okawachi, Y., Saha, K., Levy, J. S., Wen, Y. H., Lipson, M.,

and Gaeta, A. L. (2011). Octave-spanning frequency

comb generation in a silicon nitride chip. Optics let-

ters, 36(17):3398–3400.

Papp, S. B., Del’Haye, P., and Diddams, S. A. (2013). Me-

chanical control of a microrod-resonator optical fre-

quency comb. Physical Review X, 3(3):031003.

Sodre Jr, A. C., Boggio, J. C., Rieznik, A., Hernandez-

Figueroa, H., Fragnito, H., and Knight, J. (2008).

Highly efﬁcient generation of broadband cascaded

four-wave mixing products. Optics Express,

16(4):2816–2828.

Wang, Y., Leo, F., Fatome, J., Erkintalo, M., Murdoch,

S. G., and Coen, S. (2017). Universal mechanism

for the binding of temporal cavity solitons. Optica,

4(8):855–863.

Xue, X., Zheng, X., and Zhou, B. (2019). Super-efﬁcient

temporal solitons in mutually coupled optical cavities.

Nature Photonics, page 1.

Zajnulina, M., Boggio, J. C., B

ohm, M., Rieznik, A. A.,

Fremberg, T., Haynes, R., and Roth, M. M. (2015).

Generation of optical frequency combs via four-wave

mixing processes for low-and medium-resolution as-

tronomy. Applied Physics B, 120(1):171–184.

Zajnulina, M., B

ohm, M., Blow, K., Boggio, J. M. C.,

Rieznik, A. A., Haynes, R., and Roth, M. M. (2014).

Generation of optical frequency combs in ﬁbres: an

optical pulse analysis. In Advances in Optical and

Mechanical Technologies for Telescopes and Instru-

mentation, volume 9151, page 91514V. International

Society for Optics and Photonics.

Optical Frequency Comb Generated with an Amplitude Modulated Pump in Silicon Nitride Ring-resonators